附設粘滯阻尼器的高層立體車庫風振性能

鄒平波， 陳繁榮， 沈 琪， 趙 強， 李 英

(1.中國聯合工程有限公司， 浙江 杭州 310052； 2. 中南建筑設計院股份有限公司， 湖北 武漢 430071)

立體車庫是一種新的城市停車形式[1]，高層立體車庫不同于一般高層鋼結構，其內部沒有剛性樓板，在沿海地區，風荷載對于高層立體結構影響較大，容易產生較大的風振響應，附設粘滯阻尼器可以減少結構吸收風荷載能量，減小高層立體車庫的層間位移和內力。對于高層立體車庫和阻尼器減振技術，許多學者進行了研究。賀擁軍等[2]通過將水平阻尼支撐應用于立體車庫，通過地震作用下的動力時程分析，確定了最優阻尼支撐參數。周云等[3]在框剪結構隔震層中設置變性能粘滯阻尼器控制結構的地震響應和風振響應，證明了變性能粘滯阻尼器有良好的減振限位效果，工程價值良好。陶義等[4]在立體車庫中設置摩擦阻尼支撐，在地震作用下分析了摩擦耗能支撐的剛度和滑動摩擦力對結構響應的影響，獲得了摩擦耗能支撐的優化參數。

目前對高層立體車庫的抗風設計研究較少；計算風荷載響應時，設計人員一般將風荷載等效為靜荷載，沒有考慮脈動風的動力特性；在附加阻尼器至結構時，很多研究沒有排除阻尼器自身剛度對結構自振特性的影響。基于以上幾點，本文通過數值模擬方法生成總風壓時程函數，僅引入附加阻尼至結構，以減振率和風振吸收能量為風振性能指標，對改進后的高層立體車庫的抗風性能進行了探討。

1 結構計算模型

1.1 原結構有限元模型

高層立體車庫采用鋼框架結構，x向隔層布置十字形支撐，y向隔層布置人字形支撐，結構平面圖和立面圖如圖1，2所示。結構首層層高取2.5 m，其他層層高取2.2 m，結構層數20層，總高度為44.3 m。梁柱節點按剛接處理，柱底簡化為固接，柱截面型號為H300×200×8×10，x向框架梁型號為H250×150×6×8，y向框架梁型號為H200×150×6×8，結構支撐截面型號為φ95×5，鋼材采用Q235B。結構為了考慮車輛和電梯荷載，在每個梁柱節點施加800 kg的集中質量[5]。本文采用ANSYS軟件進行計算分析，材料的本構模型采用雙線性隨動強化模型，切線模量為1100 MPa。梁柱采用BEAM188單元，支撐采用LINK8單元，梁柱結點處的集中質量采用MASS21單元。

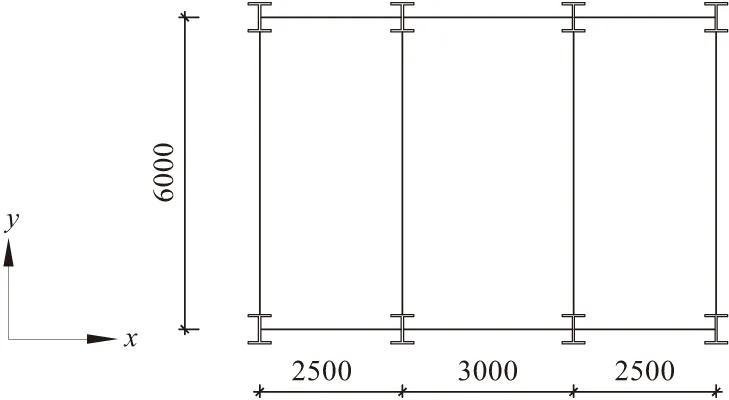
圖1 立體車庫結構平面/mm

圖2 立體車庫結構立面

1.2 粘滯阻尼器力學模型

傳統的結構減振技術主要依賴結構自身剛度以“硬抗”方式抵抗風荷載，但是隨著結構自身剛度的增加，結構吸收的風振能量也會隨之增加，對結構不利。所以附加阻尼器是控制結構風振響應的有效方法[6～9]。本文采用的粘滯阻尼器是經過粘彈性阻尼器改裝的速度型阻尼器，通過附加阻尼控制結構響應，從而減少結構吸收的風振能量。本文對開爾文模型的粘彈性阻尼器加以改進，阻尼器的力學模型如圖3所示，在ANSYS軟件中用彈簧-阻尼單元COMBIN14進行模擬[10]，計算時將COMBIN14單元的剛度常數Kd設置為0，形成粘滯阻尼器，從而結構的自振特性不會改變，僅附加阻尼起作用，則粘滯阻尼器的阻尼力fd的計算公式為：

圖3 阻尼器力學模型

fd=Cdud

(1)

式中：Cd為阻尼常數；ud為阻尼器兩端的相對位移。

粘滯阻尼器引入的附加阻尼比與阻尼常數關系密切，根據文獻[11]，選取阻尼常數Cd=1.5×108N·s/m。為了驗證結構附加阻尼器之后，自振特性不變，對原結構和附設阻尼器結構進行模態分析，結構前兩階自振周期分別為1.458，1.269 s，前后沒有發生變化。

2 風壓時程函數

AIT Maatallah等[12]通過將Hammerstein模型改編為自回歸模型，得到新的Hammerstein模型可以更好地捕捉各種風速特征。要進行風振時程分析，首先須確定總風壓時程函數。總風壓時程函數wt由兩部分組成：

wt=wa+wp

(2)

式中：wa，wp分別為平均風壓和脈動風壓。

平均風壓可以通過基本風壓反算得到，脈動風壓時程函數的獲取有實測和人工模擬[13,14]兩種方法。實測受外界條件干擾較大，記錄結果有較大誤差。人工模擬基于大量實測數據，分析數據的統計特性，獲得滿足條件的脈動風壓時程。本文采用人工模擬獲得風壓時程數據，脈動風的功率譜Davenport譜[15]的經驗公式為：

(3)

式中：n為脈動風速頻率；x=1200n/v10av；Sv(n)為風速功率譜；K為地面粗糙度系數；v10av為標準高度的平均風速。

基于以上風速功率譜，本文通過風荷載時程處理程序WINDHIST V2.0獲得風壓時程函數[15]。該程序平穩隨機過程的輸出方法采用線性濾波法中的自回歸模型(Auto Regressive Model，AR模型)，程序中平均風壓模型采用GB 50009-2012《建筑結構荷載規范》[16]的指數模型。分析過程中基本風壓取0.45 kN/m2，地面粗糙度類別取B類，時間取10 min，結構頂部的總風壓時程曲線如圖4所示。獲得結構不同樓層高度的總風壓時程后，將樓層高度處的總風壓乘以上下層層高的平均值得到沿樓層邊梁分布的線荷載，將線荷載施加到樓層邊梁上，形成結構的風荷載工況。

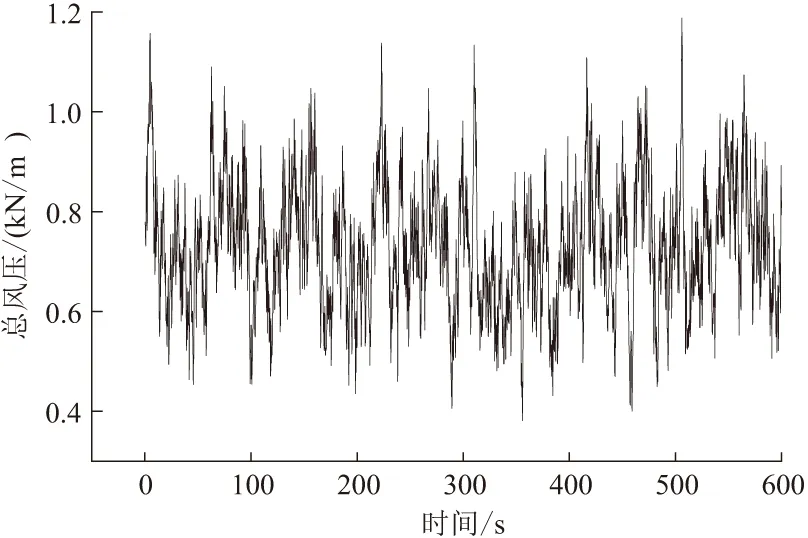
圖4 結構頂部總風壓時程函數

3 結構計算分析

3.1 結構風振性能指標

本文選取結構減振率和風振吸收能量作為風振性能分析指標，結構減振率ε定義為：

(4)

式中：θ1為附加阻尼器之后結構的最大層間位移角；θ0為原結構最大層間位移角。

結構的風振吸收能量為風荷載在結構位移中所作的功，結構的樓層位移取結構該層所有框架柱位移的平均值，結構某樓層在t時刻的風振吸收能量E(t)為：

(5)

式中：wt(t)為某樓層t時刻的總風壓；A為某樓層總風壓的受力面積；u(t)為某樓層t時刻的樓層位移。

結構的風振吸收能量為所有樓層的風振吸收能量疊加。

3.2 結構全高隔層布置阻尼器

本文采用兩類阻尼器布置方案，分別為A類和B類方案，A類方案考慮在結構全高范圍內隔層布置阻尼器，考慮四種布置形式，每層布置4個阻尼器，每種方案共36個阻尼器，阻尼器從結構第3層開始隔層布置，A類方案的四種阻尼器布置形式編號為A-1～A-4，如圖5所示。方案A-1的阻尼器兩端分別與梁柱節點和梁跨中相連，方案A-2的阻尼器兩端分別與梁柱節點和梁1/4處相連，方案A-3的阻尼器兩端分別與柱中部和梁跨中相連，方案A-4的阻尼器兩端分別與柱中部和梁1/4處相連。B類方案考慮在結構局部層數布置阻尼器，阻尼器布置形式將在3.3節中進行討論。

3.2.1 減振率

由于立體車庫沒有樓板，樓板的剛性假定并不適用于立體車庫，所以立體車庫在樓層平面內的變形不一致，故在風荷載作用下，立體車庫的角柱變形和中柱變形不一樣，由于中柱的抗側剛度大于角柱，所以層間位移較角柱小，由于兩根角柱之間設置人字形支撐，所以角柱變形時可以通過人字形支撐進行位移協調，角柱頂部位移較中柱小。4種阻尼器布置形式的減振率如表1所示，以中柱最大層間位移角為例，結構中柱最大層間位移角、結構頂部位移和風振加速度分別如圖6～8所示。

表1 四種阻尼器布置方案的減振率

圖6 中柱最大層間位移角

圖7 最大頂部位移

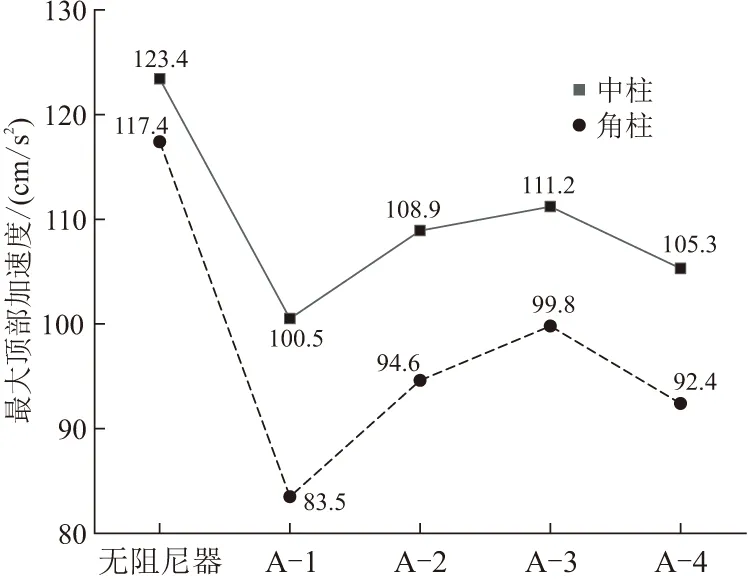
圖8 最大頂部加速度

通過以上圖表可知，附設阻尼器之后，結構最大層間位移角得到了明顯改善，其中方案A-1的減振效果最佳，中柱和角柱的減振率分別為29.2%，36.1%。且方案A-1的最大頂部位移和最大頂部加速度最小，中柱和角柱最大頂部位移分別為91.7，84.9mm，最大頂部加速度分別為100，83.5 cm/s2，四種布置形式的最大層間位移角、最大頂部位移和最大頂部加速度較原結構得到明顯改善，但減振效果沒有方案A-1明顯。其中方案A-3在這四種布置形式中減振效果略差，方案A-2和A-3次之，所以在A類方案的四種阻尼器布置形式中，方案A-1最合適。

3.2.2 風振吸收能量

根據式(4)及ANSYS的分析結果計算最大風振吸收能量和阻尼器吸收能量，兩者之差為其他構件吸收能量，如表2所示。

表2 四種阻尼器布置方案的風振吸收能量 J

結構的最大風振吸收能量和其他構件吸收能量明顯減少，其中方案A-1的最大風振吸收量和其他構件吸收能量最少，分別為2959，715 J。四種布置形式阻尼器吸收的能量差別不大，所以在受力過程中，阻尼器主要是通過限制結構的位移減少結構吸收風振能量，結構吸收的風振能量越少，在阻尼器吸收能量相同的情況下，給結構梁、柱等其他構件帶來的負擔就會明顯減少。所以從吸收風振能量角度考慮，方案A-1的布置顯得更為合理。

3.3 部分層數隔層布置阻尼器

3.3.1 減振率

為了減少阻尼器的布置數量，考慮豎向布置位置的不同，引入B類阻尼器布置方案，將阻尼器布置形式分為底部布置、中部布置和頂部布置三種布置形式，每層布置4個阻尼器，每種方案共20個阻尼器，底部布置在結構第3,5,7,9,11層隔層布置阻尼器，中部布置在結構的第7,9,11,13,15層處布置阻尼器，頂部布置在結構的第11,13,15,17,19層布置阻尼器。根據3.2節的分析結果，阻尼器樓層布置形式按方案A-1效果最好，所以此處的底部布置、中部布置和頂部布置的樓層阻尼器布置形式參考方案A-1進行布置，三種布置形式編號分別為B-1，B-2，B-3，阻尼器布置如圖5所示。三種阻尼器布置方式的風振響應如表3、圖9～11所示。

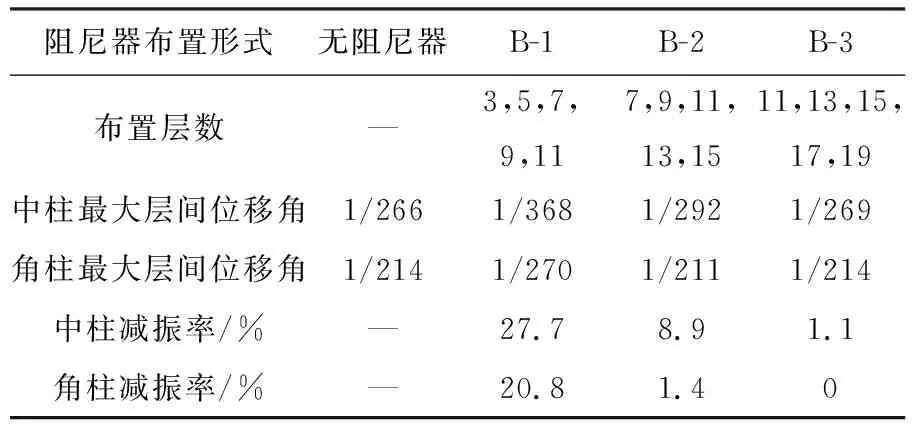
表3 三種阻尼器布置方案的減振率

圖9 中柱最大層間位移角

圖10 最大頂部位移

圖11 最大頂部加速度

由圖表可知，方案B-1的減振率優于方案B-2和B-3，同時方案B-1的最大頂部位移和頂部加速的控制效果最為明顯，方案B-1中柱和角柱的最大頂部位移分別為95.8，84.5 mm，最大頂部加速度分別為104.1，87.8 cm/s2，方案B-2和方案B-3減振率比較小，兩種布置方式中中柱的減振率分別為8.9%，1.1%，角柱的減振率分別為1.4%和0，但是這兩種阻尼器布置方式可以改善結構頂部位移和頂部加速度。所以在三種部分層數布置阻尼器方案中，優先選擇方案B-1。

方案B-1的中柱最大層間位移角和方案A-1(沿結構全高布置阻尼器)的最大層間位移角較為接近，角柱的最大頂部位移也相近，角柱最大層間位移角、中柱最大頂部位移和最大頂部加速度較方案A-1的指標還有差別，但差別不大，由此可見，如果布置阻尼器數量有限，選擇底部布置方案B-1是較好的方案。

3.3.2 風振吸收能量

底部布置方案B-1、中部布置方案B-2和頂部布置方案B-3三種方案的風振吸收能量如表4所示，隨著阻尼器布置數量的減少，阻尼器所吸收的能量也相應減少，方案B-1的其他構件吸收能量比方案B-2和方案B-3吸收的能量少，但是比A類方案四種布置形式所吸收的能量都要多，所以從其他構件所吸收的風振能量角度分析，阻尼器的布置數量起主導作用。

表4 三種阻尼器布置方案的風振吸收能量 J

4 結 論

本文針對特定的基本風壓和地面粗糙度類別，運用AR模型獲得總風壓時程函數，以20層立體車庫為研究對象，用風振時程分析方法研究了不同阻尼器布置方式對立體車庫風振性能的影響，得到最優阻尼器布置方法，分析結果顯示：

(1)通過自回歸模型模擬的總風壓時程函數可以很好地體現風荷載的動力特性，對于比較復雜的結構可以采用風振時程分析方法計算風荷載作用下的風振響應。

(2)為了得到粘滯阻尼器，可以通過使粘彈性阻尼器的剛度參數置為0，從而排除了阻尼器剛度對結構的影響，僅引入附加阻尼，這種方法可以推廣應用。

(3)在原結構附設粘滯阻尼器后，A類方案和B類方案的幾種阻尼器布置形式都有一定的減振效果。在阻尼器布置數量充足的情況下，A類方案考慮沿結構全高隔層布置粘滯阻尼器，在四種布置形式中，方案A-1的中柱和角柱的減振率分別為29.2%，36.1%，其他構件吸收的風振能量為715 J。方案A-1的最大風振吸收能量最少，由于阻尼器吸收的能量與阻尼器數量有關，這樣方案A-1的其他構件吸收能量也最少。所以從減振率和吸收的風振能量來看，方案A-1效果最好。

(4)結構吸收的風振能量與阻尼器數量有直接關系，如果為了節省阻尼器數量，應該選擇底部布置(第3,5,7,9,11層隔層布置)阻尼器的方案B-1，頂部布置方案B-2和中部布置方案B-3對于原結構的風振響應沒有太大的改觀，而底部布置方案B-1使結構風振響應明顯減小，中柱和角柱減振率分別為27.7%，20.8%，可以兼顧經濟和減振的要求。