地震反應譜長周期分量對大跨度橋梁地震反應的影響

宋愛民， 常付平， 葉愛君

(1. 同濟大學 土木工程防災國家重點實驗室， 上海 200092； 2. 上海市政工程設計研究總院(集團)有限公司， 上海 200092)

目前，世界各國的橋梁抗震設計規范都將反應譜法作為地震反應分析的基本方法，但是由于缺乏真實有效的長周期地震記錄，各國抗震規范只對自振周期較短的結構給出了反應譜計算公式[1,2]。歐洲抗震設計規范NF P06-030-1/NA-2013《Eurocode 8: Design of Structures for Earthquake Resistance》規定了自振周期在4 s之前的加速度反應譜計算公式，建議4 s后的加速度反應譜由位移反應譜值根據擬譜關系得到[3]；美國橋梁抗震設計指南《AASHTO Guide Specifications for LRFD Seismic Bridge Design》規定的加速度反應譜無最大周期的限制，但指出當結構自振周期超過3 s后，規范規定的加速度反應譜譜值會偏保守[4]；我國JTG/T 2231-01-2020《公路橋梁抗震設計規范》(以下簡稱《公規》)規定的加速度反應譜最大周期為10 s[5]，CJJ 166-2011《城市橋梁抗震設計規范》(以下簡稱《城規》)的設計加速度反應譜引自GB 50011-2010《建筑抗震設計規范》(以下簡稱《建規》)，規定的加速度反應譜最大周期為6 s[6]。

近年來，我國興建了眾多的大跨度索支撐橋梁，基本周期常常超過10 s[7,8]，采用設計規范反應譜進行地震反應分析存在長周期譜值的確定問題。在實際工程中，為提高結構的抗震安全度，往往對規范的設計加速度反應譜曲線超出周期范圍部分做平臺化處理，但這會導致結構的地震反應過大，設計過于保守。

為了建立長周期結構的設計反應譜，國內外學者做了一些研究。耿淑偉等[9]通過對實際觀測的955條地震動記錄進行統計分析，以均方誤差最小原則擬合標準化反應譜，建議對于周期T大于6 s的加速度反應譜按T-1的速率下降到10 s。方小丹[10]根據位移反應譜與加速度反應譜的擬譜關系，對《建規》規定的加速度反應譜下降段進行了修正，建議加速度反應譜第一下降段(速度下降段)可簡單地按照T-1的規律衰減，第二下降段(位移下降段)按照T-2的規律衰減，并將反應譜周期延長至10 s。邱立珊[11]基于汶川地震記錄的遠場長周期地震動，對《建規》加速度反應譜第二下降段特征點周期及譜曲線進行修正，提出了包含5個待標定參數的長周期加速度反應譜模型，直至10 s。

為了分析地震加速度反應譜的長周期分量對大跨度橋梁地震反應的影響，本文首先對中美橋梁抗震設計規范的地震加速度反應譜的長周期部分進行比較分析，然后基于實際地震記錄的加速度反應譜，對我國《城規》的加速度反應譜長周期部分提出修正建議。接著，以一座主跨428 m的三塔自錨式懸索橋為例分析地震加速度反應譜長周期分量對橋梁結構不同地震反應分量的影響，并檢驗修正建議的合理性，以期供工程實踐參考使用。

1 規范地震加速度反應譜的長周期分量取值建議

1.1 中美規范加速度反應譜與實際地震記錄反應譜的比較分析

美國橋梁抗震設計規范《AASHTO Guide Specifications for LRFD Seismic Bridge Design》(以下簡稱《美規》)規定加速度反應譜如式(1)所示。

(1)

式中：SDS，SDI分別為周期0.2，1 s對應的設計加速度反應譜譜值，由場地條件決定；T0=0.2SDI/SDS；Ts=SDI/SDS。由式(1)可知，《美規》加速度反應譜長周期部分以T-1的規律衰減[4]。

我國《城規》的加速度反應譜譜值S如式(2)(3)所示。

(2)

Smax=2.25A

(3)

式中：A，Tg分別為地震峰值加速度與特征周期；η2為結構阻尼調整系數；γ，η1分別為特征周期至5倍特征周期區段曲線衰減指數和5倍特征周期至6 s區段直線下降段下降斜率調整系數[6]。

我國《公規》的加速度反應譜譜值S(T)如式(4)(5)所示。

(4)

Smax=2.5CiCsCdA

(5)

式中：T0為反應譜直線上升段最大周期，取0.1 s；Ci，Cs，Cd分別為結構重要性系數、場地系數與阻尼調整系數[5]。

根據《城規》確定一條加速度反應譜，其中，設計地震動加速度峰值為1.6 m/s2，特征周期為0.85 s，結構阻尼比為0.02，阻尼調整系數取1.47，γ與η1分別取1與0.02。以此加速度反應譜作為目標譜，在PEER數據庫中挑選了7條實際地震動，具體信息見表1。七條實際地震動對應的加速度反應譜與其均值如圖1所示。此外，根據《美規》確定一條加速度反應譜(周期0～15 s)，該反應譜前6 s的譜值與上述《城規》加速度反應譜接近；將《城規》加速度反應譜延長至15 s，其中 6 s后的譜值與6 s時相同；根據《公規》確定一條加速度反應譜(周期至15 s)，該反應譜前6 s的譜值與《城規》加速度反應譜接近，10 s后譜值與10 s時相同。圖2給出《美規》、延長后的《城規》、延長后的《公規》加速度反應譜和實際地震動加速度反應譜的平均值對比，將上述4條加速度反應譜根據擬譜關系擬合成位移反應譜，如圖3所示。

表1 強震加速度記錄

圖1 實際地震動加速度反應譜

圖2 加速度反應譜對比

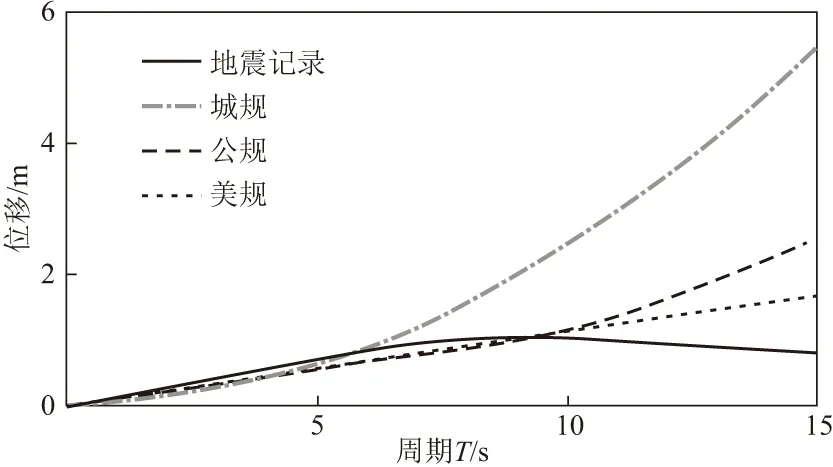
圖3 位移反應譜對比

由圖2可知，《城規》加速度反應譜如果長周期部分按平臺化處理，則譜值比《美規》《公規》和地震記錄加速度反應譜大很多，且差值隨周期的增長不斷變大；而《美規》和地震記錄加速度反應譜在長周期段較為接近。可見，《城規》加速度反應譜如果長周期段取平臺會過于保守，實際地震動加速度反應譜在長周期段近似為周期倒數的一次函數。由圖3可知，《城規》加速度反應譜如果長周期段取平臺，對應的位移反應譜在長周期段以T2的規律上升，上升規律明顯不滿足相對位移譜統計特征，且長周期段譜值遠大于實際地震動位移譜值；《美規》對應的位移反應譜以周期一次函數的規律上升，《美規》在長周期段對地震記錄位移譜模擬較好，且譜值略大于地震記錄位移譜，具有一定的安全度。

1.2 《城規》加速度反應譜的長周期修正建議

現行《城規》只對自振周期在6 s之內的結構給出了反應譜計算公式，如果對規范設計反應譜超出周期范圍部分取平臺，則長周期部分位移譜會嚴重偏離實際。由于《美規》加速度反應譜長周期段以T-1規律衰減，對應的位移譜在長周期段對地震記錄位移譜模擬較好，建議《城規》6 s后加速度反應譜按式(6)計算，其中，S6為6 s的加速度反應譜譜值。將《美規》、地震記錄和建議的加速度反應譜對比，如圖4所示。并將上述3條加速度反應譜根據擬譜關系擬合成位移反應譜，如圖5所示。由圖4，5可知，建議的《城規》加速度和位移反應譜長周期段稍大于《美規》，而且顯著大于實際地震記錄，已有足夠的安全度。

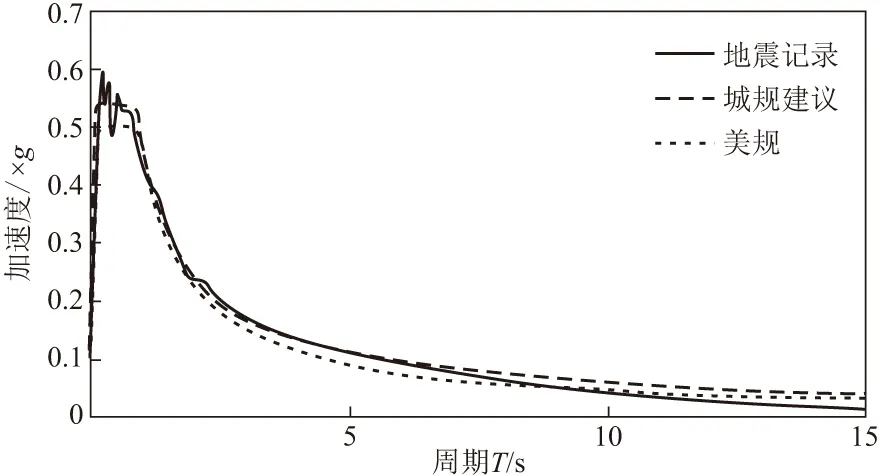
圖4 加速度反應譜對比

圖5 由擬譜公式得到的位移反應譜

(6)

2 大跨度橋梁計算模型及動力特性

為了定量分析反應譜長周期分量對大跨度橋梁不同地震反應分量的影響，本文以一座主跨為428 m的三塔自錨式懸索橋為例，建立了計算模型用于地震反應分析。

2.1 背景工程簡介

某大跨橋梁采用三塔雙索面組合梁自錨式懸索橋方案，全長約1332 m，跨徑布置為：70+168+428+428+168+70=1332 m，如圖6所示。主梁為鋼-混凝土疊合梁結構，梁高4 m，標準段全寬58.7 m。三個橋塔均為A型塔，塔身為鋼結構，塔座為混凝土結構，中塔塔身高114.58 m，塔座高9.09 m，邊塔塔身高110.6 m，塔座高3 m。各塔(墩)均采用群樁基礎，為鉆孔灌注樁并按嵌巖樁設計，樁徑為2.0 m。各塔(墩)與主梁間均設置縱向滑動、橫向固定支座。

圖6 主橋立面/m

2.2 動力分析模型

基于SAP2000平臺，建立了該橋的有限元動力分析模型，建模時考慮了邊界聯對主橋的影響。總體模型如圖7所示。主梁、主塔、塔座和承臺根據實際截面尺寸以框架單元模擬；主纜和吊桿采用桁架單元模擬，并通過主從約束與吊桿相連接。主纜、吊桿和主塔考慮了恒載作用對結構幾何剛度的影響，二期恒載以線質量的形式加在梁單元上[12]。采用六彈簧模型模擬各群樁基礎的影響，如圖8所示。各塔(墩)與主梁間縱向自由，橫向固定約束，為漂浮體系。

圖7 懸索橋動力分析模型

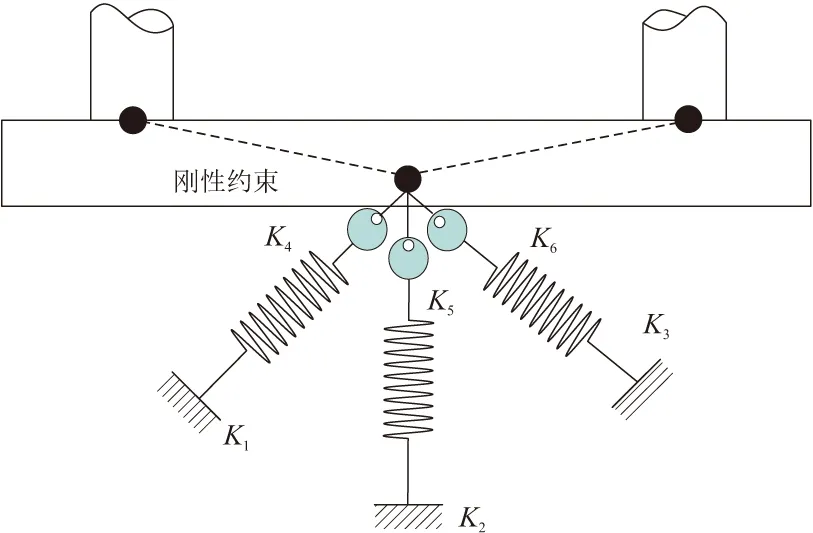
圖8 群樁基礎六彈簧模型

2.3 橋梁動力特性

對上述模型進行動力特性分析，表2給出了前5階振型的周期和模態，結果表明：橋梁結構的基本周期(縱飄)為12.65 s，遠大于《城規》反應譜的最大周期6 s。結構前5階振型皆為縱向或豎向振動，故反應譜長周期分量對橋梁的縱向反應影響較為顯著。

表2 某懸索橋結構動力特性

3 加速度反應譜長周期分量對大跨度橋梁地震反應的影響

本文基于前述計算模型，分別將現行《城規》(6 s后取平臺)、《公規》(10 s后取平臺)、《美規》、地震記錄和《城規》(修訂)的加速度反應譜作為地震輸入，通過比較不同輸入下的橋梁結構地震反應來分析加速度長周期分量對橋梁地震反應的影響。

在進行地震反應譜分析時，分別計算考慮600階貢獻和僅考慮基本振型貢獻橋梁結構的地震反應。地震動輸入為上文提到的5種加速度譜，輸入方式為縱橋向+豎向，振型組合方法采用CQC(Complete Quadratic Combination)法，方向組合方法采用SRSS(Square Root of Sum of Square)法。表3，4給出了考慮前600階振型貢獻時在不同反應譜輸入下橋梁墩柱關鍵截面內力、橋梁關鍵位移的對比關系。

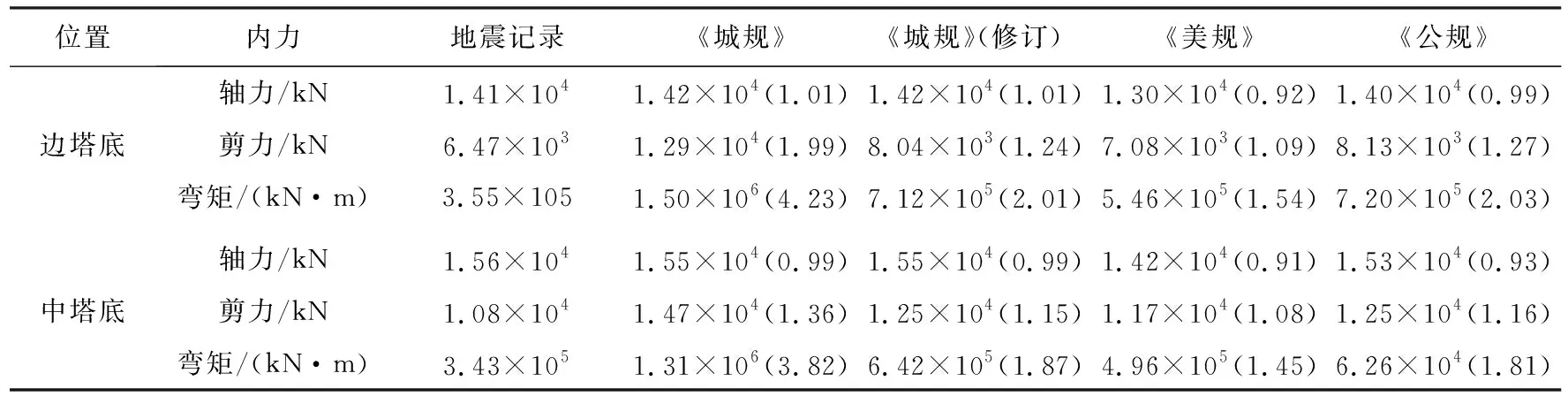
表3 不同反應譜輸入下橋塔縱向地震內力

由表3可知，橋塔軸力在《城規》《公規》《美規》和《城規》(修訂)反應譜輸入下相差不大，與地震記錄反應譜輸入下的軸力相比誤差均在10%之內，故軸力對加速度反應譜長周期分量不敏感；在不同反應譜輸入下塔底彎矩差別較大，《城規》《公規》《城規》(修訂)和《美規》輸入下邊塔的彎矩是地震記錄反應譜輸入下邊塔彎矩的4.23，2.03，2.01，1.54倍，這說明縱橋向塔底彎矩對加速度反應譜長周期分量十分敏感。由表4可知，《城規》《公規》《城規》(修訂)和《美規》反應譜輸入下梁端位移是地震記錄反應譜輸入下梁端位移的4.26，2.00，2.03，1.57倍，說明加速度反應譜長周期分量對梁端縱向位移影響十分大。與地震記錄反應譜輸入下的結果相比，《城規》輸入下塔底彎矩與主梁位移較大，說明對規范加速度反應譜超出周期范圍部分取平臺段，會造成縱向地震作用下塔底彎矩和主梁位移的幾倍增加；對《城規》加速度反應譜長周期部分提出修正建議后，相比于《城規》輸入下的反應，結構地震反應減少50%，但仍有足夠的安全儲備。

表4 不同反應譜輸入下橋梁關鍵位移 m

為進一步驗證加速度反應譜長周期分量對結構反應的影響，計算基本振型對結構地震響應的貢獻。表5，6列出了僅考慮基本振型的結構反應及與考慮600階振型結構反應的對比，表7列出了各反應譜基本周期所對應的譜值。

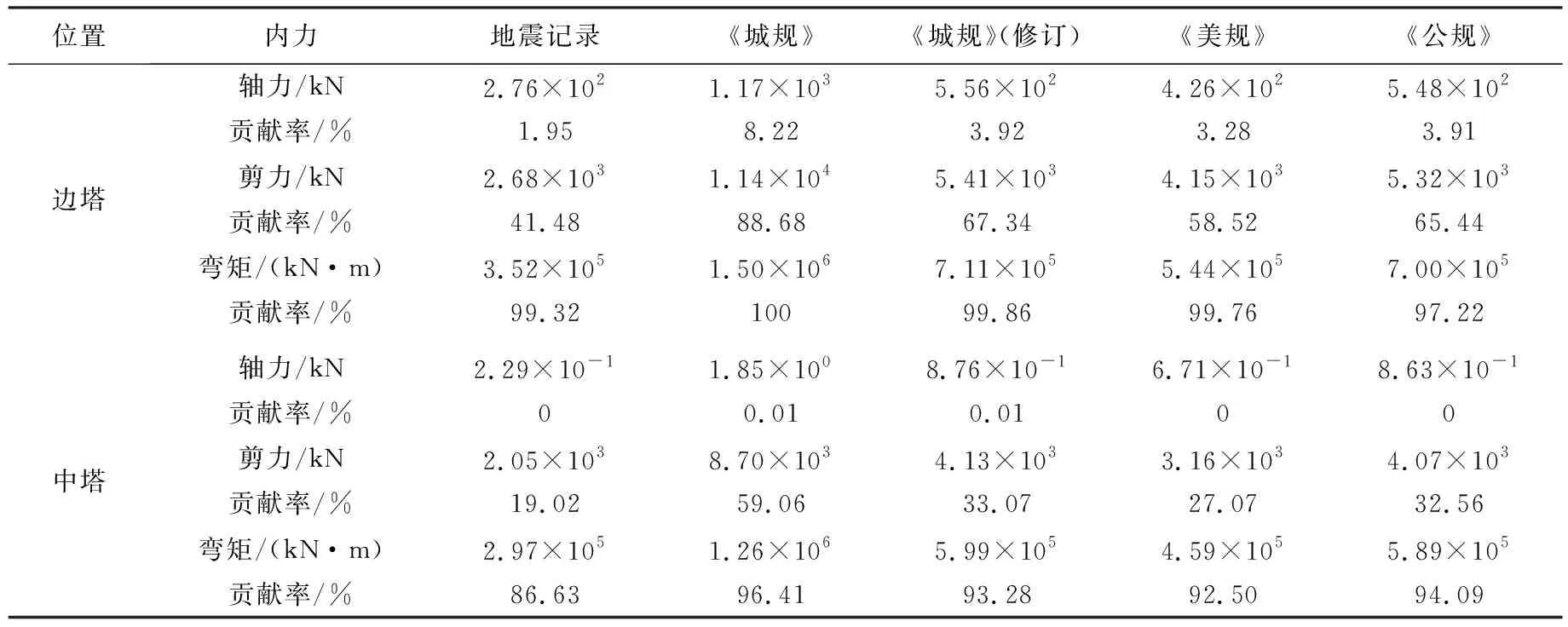
表5 基本振型對橋塔內力的貢獻

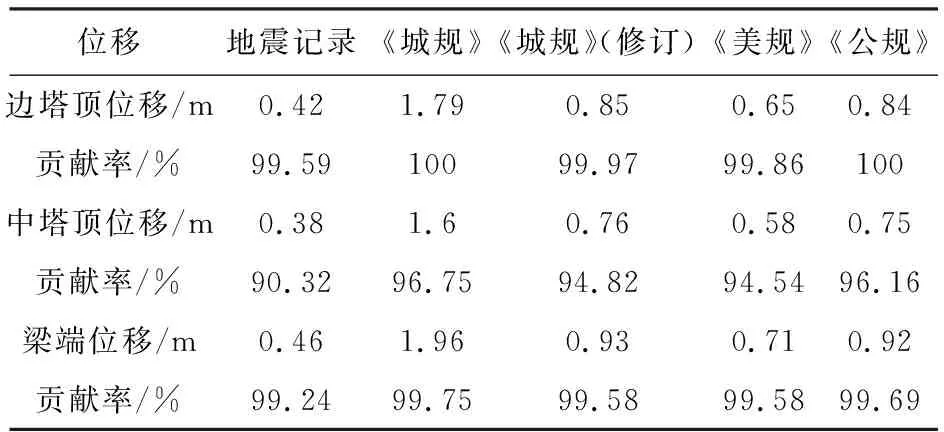
表6 基本振型對橋梁關鍵位移的貢獻

表7 基本周期對應的反應譜譜值

由表5可知，在不同反應譜輸入下，僅考慮基本振型橋塔的軸力占考慮600階振型橋塔軸力的比例均在9%以內，說明基本振型對橋塔軸力貢獻較小，也驗證了軸力對加速度譜長周期分量不敏感；在不同反應譜輸入下，僅考慮基本振型橋塔的彎矩占總彎矩的比例較大，均在85%以上。由表6可知，在不同反應譜輸入下，由基本振型貢獻的梁端位移占比均在99%以上。綜上，加速度反應譜長周期分量會顯著影響縱向地震輸入下大跨度索支撐橋梁的橋塔彎矩與梁端位移。綜合表5～7，不同反應譜輸入下橋塔的彎矩與基本振型對應的不同加速度反應譜譜值分布規律一致；不同反應譜輸入下梁端的位移與基本振型對應的不同位移反應譜譜值分布規律一致。故反應譜長周期段譜值規定不能過于保守，要符合實際地震動統計規律。

4 結 論

本文對比了中美橋梁抗震設計規范反應譜的長周期部分，并對《城規》反應譜長周期段提出了修正建議；以一座主跨為428 m的三塔自錨式懸索橋為例，分析反應譜長周期分量對橋梁結構不同地震反應分量的影響。得到以下結論：

(1)《城規》加速度反應譜6 s后如果拉平，對應的位移反應譜長周期段增長規律顯著大于實際地震動位移譜統計規律，且周期越大，位移譜譜值相差越大。根據已有文獻和7條實際地震動加速度反應譜均值，建議6 s后加速度反應譜按周期倒數的一次方關系衰減。

(2)對于漂浮體系大跨度索支撐橋梁，一階縱飄振型對塔底縱向彎矩與梁端縱向位移貢獻分別達85%與99%以上，可見加速度譜長周期分量顯著影響結構墩柱彎矩與梁端位移。

(3)如果對《城規》設計反應譜超出周期范圍部分取平臺段，會造成縱向地震作用下塔底彎矩和主梁位移的幾倍增加，按建議的周期倒數一次方關系衰減，可避免過度放大結構反應，但與地震記錄輸入下的反應相比仍具有一定的安全度。