表面粗糙峰坐標點云重構的金屬-橡膠接觸分析

鄒龍慶，黃聰聰，付海龍,2，王玥

（1.東北石油大學 機械科學與工程學院，黑龍江 大慶 163318；2.東北石油大學 環渤海能源研究院，河北 秦皇島 066004）

橡膠和硬基材之間的摩擦接觸廣泛存在于工業生產中。真實機械加工表面實際上是由大量形狀不一的微凸體構成[1]，接觸通常只發生在微凸體上，導致接觸不連續，真實接觸面積遠小于理論接觸面積，如圖1 所示[2]。表面形貌對接觸界面之間的接觸狀態、摩擦磨損等有很大影響[3-4]。

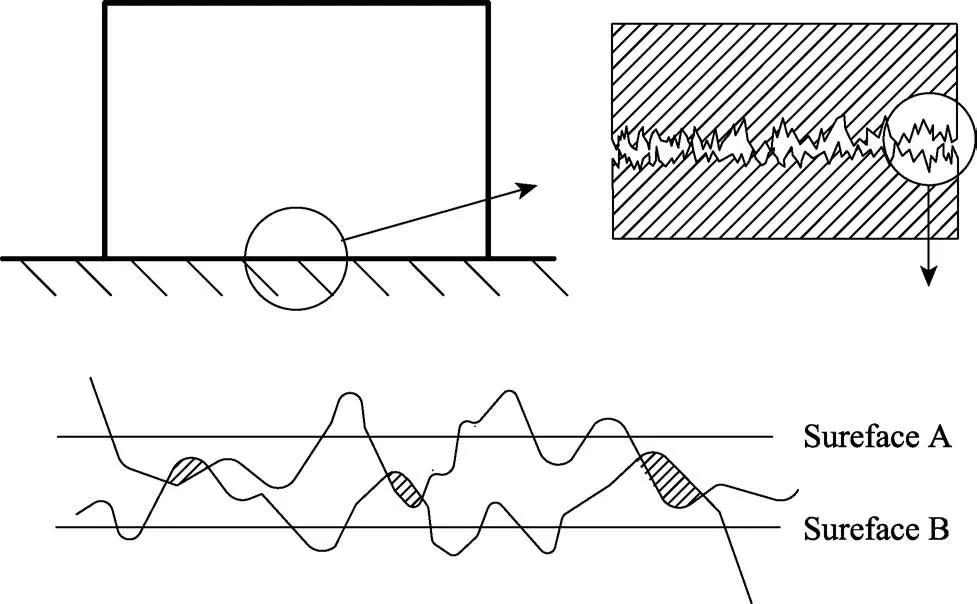
圖1 真實粗糙表面的接觸形式[2]Fig.1 Real rough surface contact[2]

Greenwood 和Williamson[5]假設所有的微凸體都有相同的曲率半徑，且其高度在均值附近隨機分布，將Hertz 模型推廣至隨機粗糙表面。國內外學者[6-10]將G-W 模型成功用于兩個粗糙表面間的接觸問題的研究。理想的接觸模型應盡可能全面地包含原始的形貌信息，以更加精準地表征粗糙表面。研究發現，有限元接觸分析是一種準確模擬接觸過程中表面粗糙峰、谷相互作用的有效手段[11]。Pei[12]通過剛性平面和分形表面之間的有限元計算，發現接觸面積與施加載荷呈正相關。Kogut[13]得到了零件表面接觸力與接觸面積的近似方程。Yastrebov[14]基于簡化的彈塑性材料和剛性平面的接觸模型，通過建立剛-柔接觸，分析載荷-位移曲線，獲得了真實的接觸面積。賴聯鋒[15]研究了微凸體曲率半徑對粗糙表面磨損量的影響。

上述研究較好地完成了剛性平面-柔性表面接觸問題研究，但是針對金屬-橡膠的接觸問題，因橡膠材料的超彈性[16]和非線性[17]，使金屬和橡膠表面每對微凸體的接觸都呈現非線性特征。從微觀角度看，除了要考慮粗糙峰沿高度上的分布外，其空間分布也不應被忽略[18]。故通過接觸面積確定兩個粗糙面間的范德華力，描述其接觸狀態，并確定界面間磨損粒子的形成方式具有科學意義。因此，本文以G-W 模型為依據，通過獲取金屬-橡膠接觸面的坐標點云，以重構實際粗糙表面，獲得外部載荷、接觸面積、接觸狀態三者之間的關系，探究金屬-橡膠接觸過程中，表面粗糙度和外部載荷對其接觸界面摩擦磨損特性的影響。

1 粗糙表面的彈性接觸理論

圖2 為兩個隨機粗糙表面的接觸模型[19]，當z＞h時，兩表面發生接觸，其發生概率為：

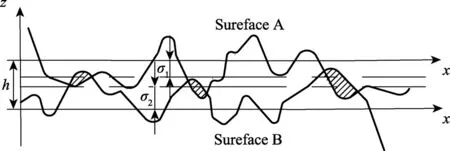
圖2 兩隨機粗糙表面接觸Fig.2 Contact of two random rough surfaces

若隨機表面的微凸體數為n，則產生接觸的微凸體數m為：

由Hertz 接觸模型，單個微凸體的接觸面積AΔ 為：

則實際接觸面積rA為：

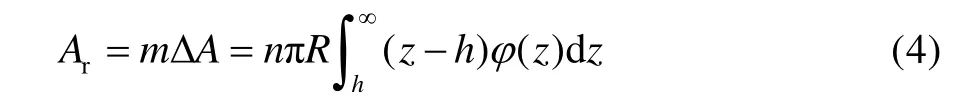
單個微凸體承受的載荷pΔ 為：

則微凸體承受的總載荷p為：

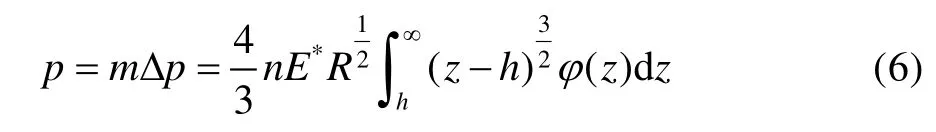
假設粗糙表面輪廓高度服從高斯指數型分布，令φ(z) = exp( -z/σ)，則有：

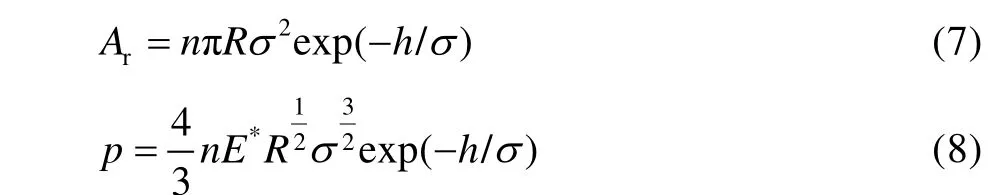
2 粗糙表面重構

目前，通過有限元建模對接觸表面進行描述的主流方法包括：確定性描述[20]、分形描述[21]、統計描述[22-23]。前兩種方法通常受限于測量裝置的精度，后者則利用統計學方法將一個包含多尺度信息的粗糙表面簡化為單一尺度，大大降低了建模成本。為此，本文基于統計描述法，通過自相關函數和高度分布函數[24]獲得隨機粗糙表面數據云點的坐標值，再利用ANSYS 對粗糙表面進行重構，具體思路如圖3 所示。

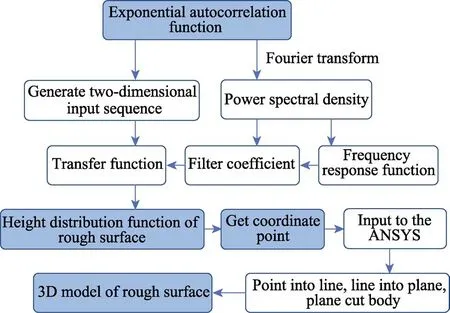
圖3 粗糙表面重構過程Fig.3 Process of rough surface reconstruction

圖4a 為利用高度分布函數和自相關函數在MATLAB中重構的粗糙表面坐標點云分布，圖4b 為所生成表面的高度分布。分別建立表面粗糙度為1.6 μm 和3.2 μm的金屬-橡膠模型，進而得到M1.6-R1.6、M1.6-R3.2、M3.2-R1.6、M3.2-R3.2（M 表示金屬，R 表示橡膠，下同）的4 組裝配模型。圖5 為ANSYS 有限元模型重構過程及裝配結果，其中橡膠的尺寸為100 μm ×100 μm×40 μm，金屬的尺寸為100 μm ×1 00 μm × 1 0 μm 。

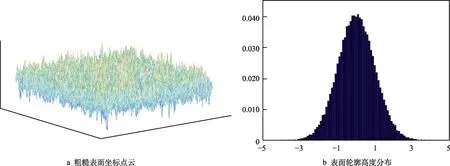
圖4 粗糙表面的統計學描述Fig.4 Statistical description of rough surfaces: a) rough surface coordinates; b) height distribution of surface

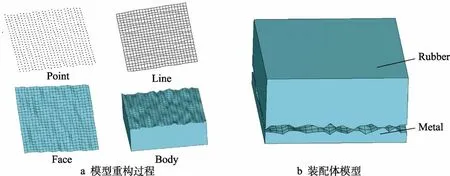
圖5 隨機粗糙表面接觸模型Fig.5 Geometric model of random rough surface contact: a) model reconstruction process; b) assembly model

3 接觸分析

3.1 有限元模擬

對金屬-橡膠接觸進行分析時，金屬選用結構鋼，橡膠為丁腈橡膠，采用Mooney-Rivlin 本構模型[25]，選擇的參數為：C10=4.622 MPa，C01=–1.548 MPa，D1=0.006 54。由于二者硬度相差較大，所以設置結構鋼為剛體，橡膠為柔性體，在網格劃分時，剛體只會在接觸表面生成網格，提高計算效率。接觸問題和橡膠材料的非線性特征導致接觸分析求解收斂困難，因此除局部加密外，還應設置低階單元，并引入非線性自適應網格，以提高其收斂性，網格劃分結果如圖6 所示，共產生73 294 個節點，391 070 個單元。用SOLID186單元定義實體，用TARGE170 單元定義目標面，用CONTA174 單元定義接觸面，形成接觸對如圖7 所示。在剛體底部施加“體-地面”綁定約束，在橡膠側面施加位移約束，同時釋放z方向的自由度，在橡膠頂面施加不同數值的法向載荷p。此外，還應通過調整初始接觸狀態、接觸剛度和打開大變形等手段來提高計算的準確性。

圖6 網格劃分及接觸面網格細化Fig.6 Mesh division and refinement of contact surface

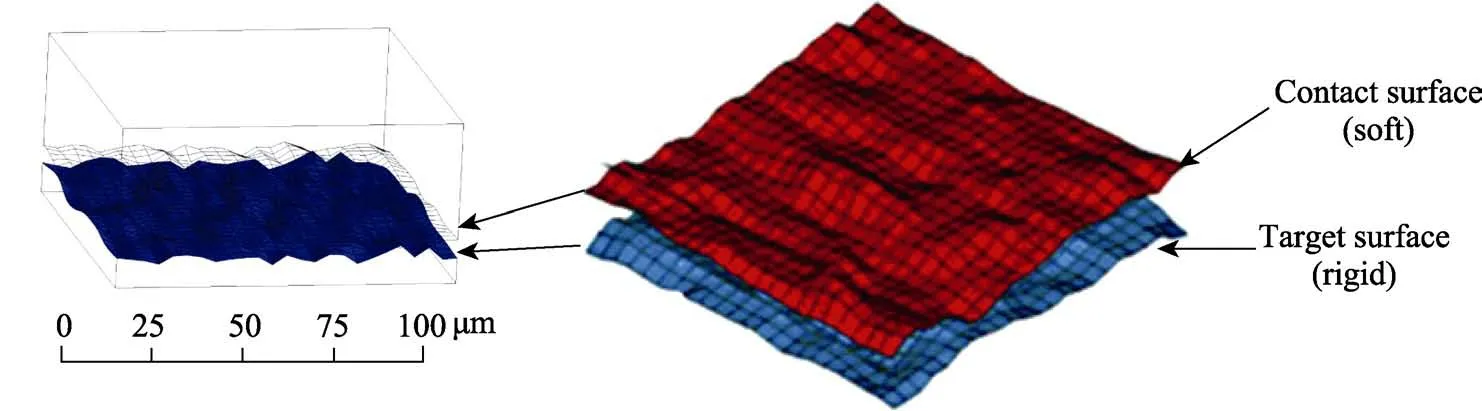
圖7 接觸界面模型Fig.7 Model of contact interface

3.2 結果與分析

如前所述，接觸表面間的真實接觸面積與摩擦、磨損等諸多物理現象有著密切聯系，因此獲得載荷和接觸面積之間的映射關系，一直是粗糙表面接觸分析所關注的重點[26-27]。圖8 為不同載荷作用下M1.6-R1.6模型的接觸面積云圖。可以直觀地看到，接觸面積隨外加載荷的增加而增加。考慮到微觀表面微凸體的相互作用，兩表面在低載荷下發生接觸時，部分較高的微凸體首先發生接觸，并很快產生較大變形，其接觸應力到達屈服極限而產生塑性變形，此后接觸點的應力不再變化，當載荷持續增大時，只能讓更多的微凸體產生接觸，直到能完全支持外部載荷為止。

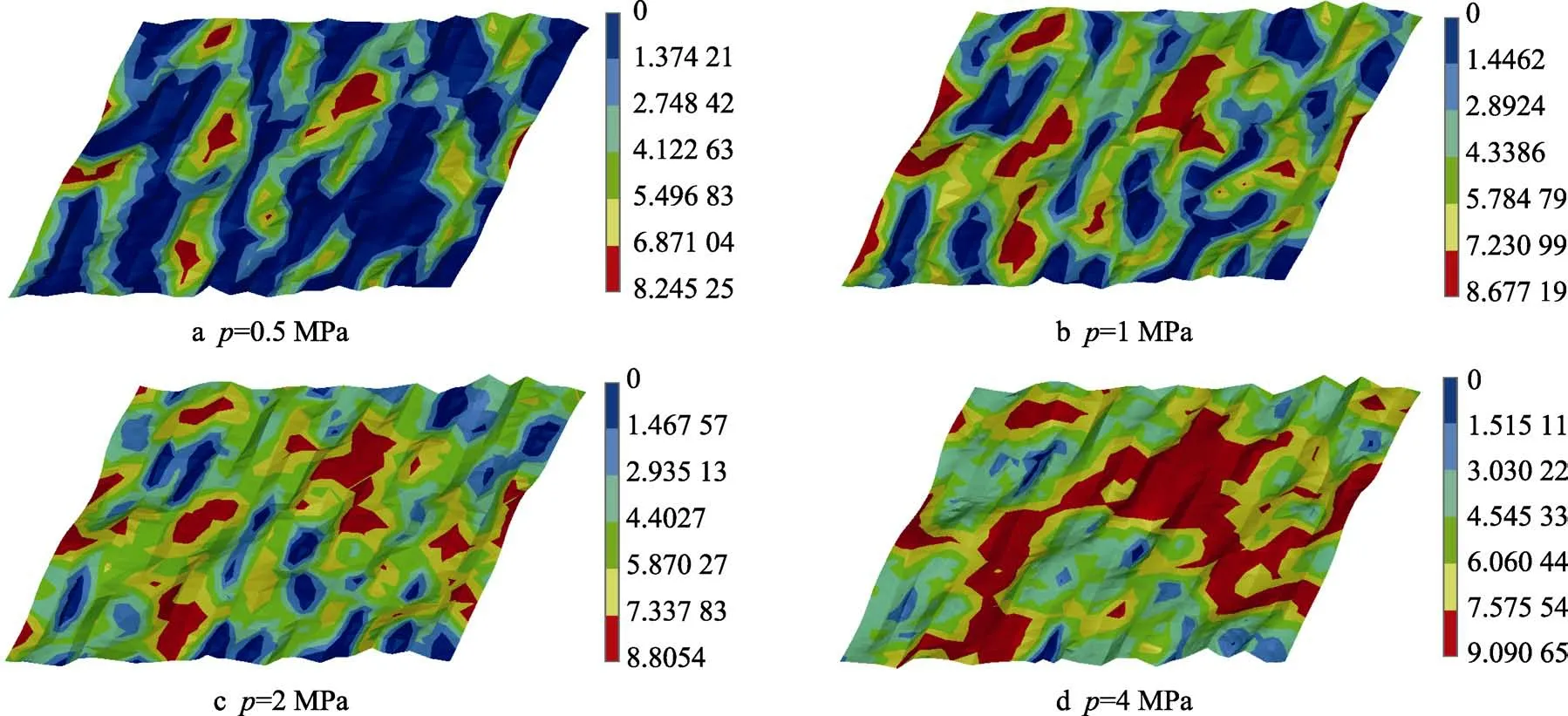
圖8 不同載荷下M1.6-R1.6 模型的接觸面積云圖Fig.8 Model M1.6-R1.6 contact area under different loads

隨著外部載荷的增加，界面間接觸面積呈非線性增加，如圖9 所示。載荷較低時，外加載荷每增加0.1 MPa，接觸面積增加6%左右；載荷較大時，外加載荷每增加0.1 MPa，接觸面積增加1.5%左右。同一載荷不同粗糙度的接觸表面，粗糙度越大，接觸面積越小。分析認為，表面粗糙度越大，微凸體之間的高度差就越大，隨著載荷的增加，在達到屈服極限之前，彈性體產生的形變也越大，所承受的載荷也更多，因此后續承受載荷產生接觸的微凸體數目相對減少，真實接觸面積也就減小。

圖9 不同粗糙度表面外部載荷與接觸面積的關系Fig.9 Relationship between surface loads with different roughness and contact area

Yashima[28]利用特殊模具制得了微凸體隨機分布的橡膠表面，研究了其與光滑剛性透鏡之間的接觸情況，通過對微觸點處的透射光進行成像，測量不同載荷下的真實接觸面積，發現二者呈冪指關系。因為玻璃-橡膠和金屬-橡膠都是典型的剛柔接觸，所以本文用指數關系來對仿真數據進行擬合，即：

其中，待定系數a和b由材料屬性和表面形貌確定。利用Levenberg-Marquardt 算法對圖9 中的數據進行非線性擬合，結果見表1，發現4 種模型的相關系數均大于0.99。

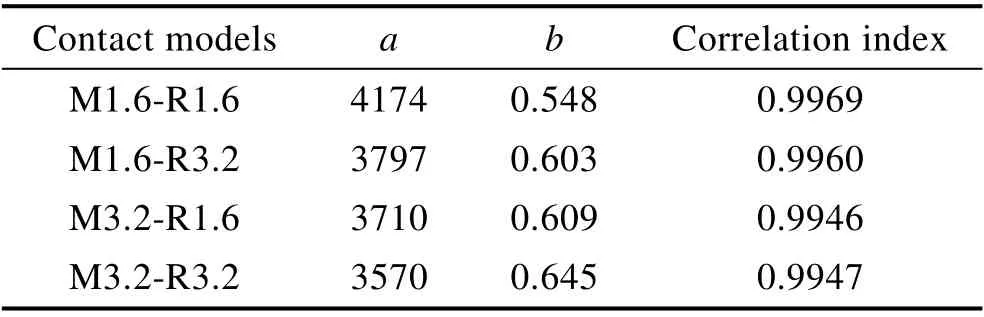
表1 4 種接觸模型的參數Tab.1 Parameters of the four contact models

根據式（9）和表1 中參數a、b的值，得到不同粗糙度表面接觸時接觸面積和外部載荷的關系。從式（10）—（13）可以發現，載荷較低時，接觸面積將隨著表面粗糙度的增加而減小，當載荷足夠大時，接觸面積會隨著表面粗糙度的增加而增加，且其趨勢越來越明顯。通常情況下，理論接觸面積相同時，粗糙度大的表面，其實際面積也更大。假設在某一載荷作用下，產生接觸的微凸體數目不變，若繼續增加載荷，粗糙表面體積較大的微凸體會貢獻更大的接觸面積，使接觸面積隨粗糙度的增加而增大。

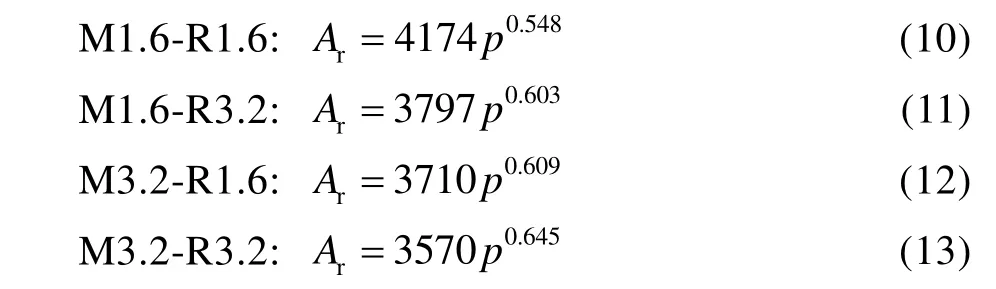
根據上述接觸非線性分析，按接觸面距目標面的距離大小，將接觸分為遠離、近場、粘著、滑移4 種狀態。圖10 為不同載荷下M1.6-R1.6 接觸模型的接觸狀態云圖，紅色表示發生接觸的微凸體面積（粘著狀態），黃色部分則為非接觸面積（近場狀態），藍色邊界則為二者的過渡區域（滑移狀態）。隨著外部載荷和表面粗糙度的改變，界面接觸狀態發生了顯著變化，近場接觸明顯減少，粘著接觸明顯增加。

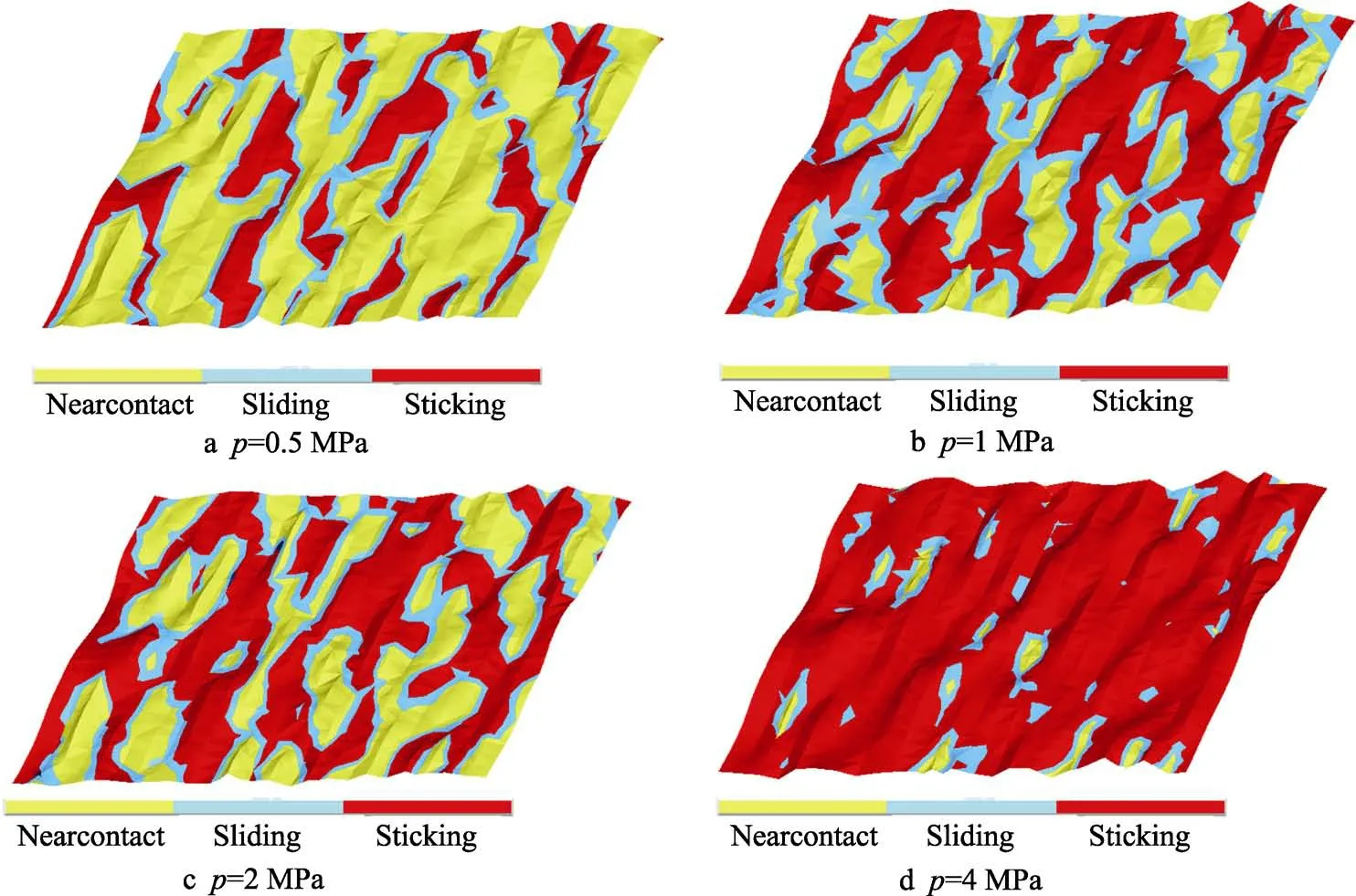
圖10 不同載荷下M1.6-R1.6 模型的接觸狀態Fig.10 Contact state Model M1.6-R1.6 under different loads

圖11 描述了不同載荷下界面接觸狀態的變化趨勢。載荷較小時，接觸狀態以近場接觸為主，占接觸界面的75%以上，滑移和粘著的占比均在10%左右。隨著載荷的增加，近場接觸的占比先呈線性下降，后趨于平緩；粘著接觸的占比變化呈現出與近場接觸完全相反的趨勢；滑移接觸的占比變化趨勢整體比較平緩，在12%左右浮動。分析認為，上述現象的產生源于橡膠的彈性模量較小，微凸體在外加載荷的作用下易發生變形，近場接觸逐漸向下一接觸狀態過渡。隨著外加載荷的持續增加，橡膠微凸體會持續變形，與金屬微凸體發生錯峰滑移，因此滑移接觸占比逐漸增加。由于橡膠材料的超彈特性，最開始產生接觸的橡膠微凸體，完全填充到金屬粗糙表面的凹谷中，并相互嚙合，不再產生相對位移，近場接觸和滑移接觸大部分都過渡成粘著接觸。

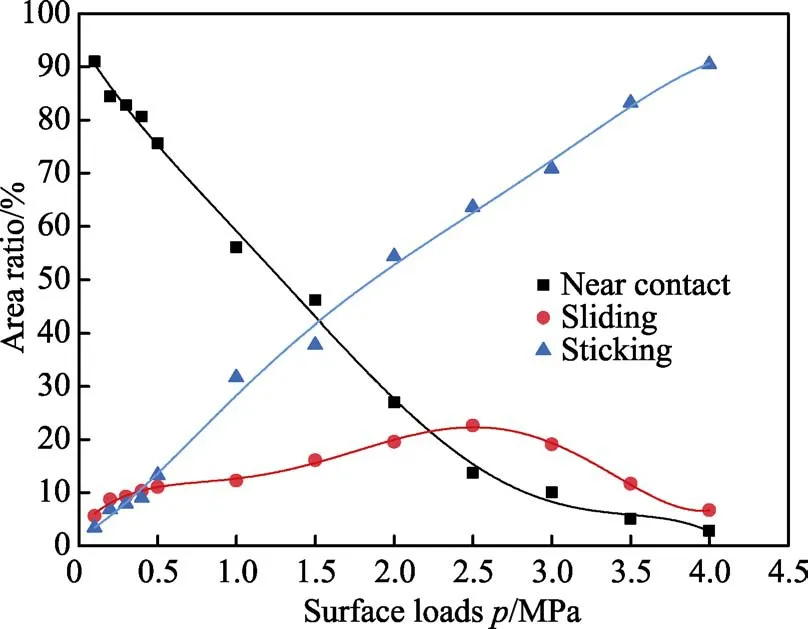
圖11 同一模型接觸狀態隨載荷的變化曲線Fig.11 Curve of contact state with load for the model

圖12 為不同粗糙度表面接觸狀態隨載荷的變化趨勢。實際上，近場接觸對于磨損的影響甚微，這里著重討論滑移接觸和粘著接觸隨粗糙度變化的趨勢。對于粘著接觸，當載荷較小時，接觸中發生粘著的面積占比相差不大；當載荷較大時，接觸界面更加粗糙，發生粘著接觸的占比越低。分析認為，粗糙度越大，微凸體的體積就更大，因此需要消耗更多的能量才能使界面間的接觸狀態從滑移接觸過渡到粘著接觸。對于滑移接觸，表面越粗糙，滑移接觸占比越高。這是因為微凸體的高度差越大，外加載荷作用下，微凸體之間的滑移距離就越大，滑移接觸占比也隨之增加。

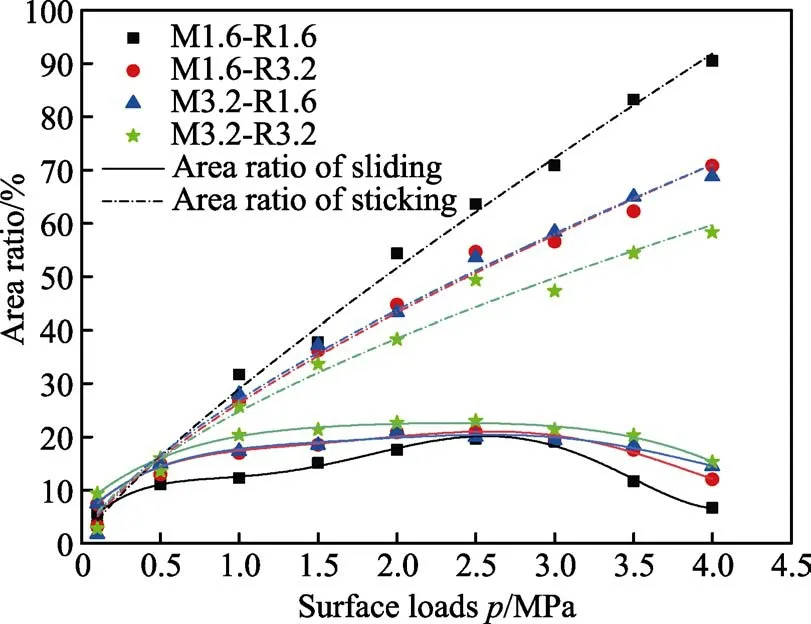
圖12 接觸狀態隨粗糙度的變化曲線Fig.12 Curve of contact state with roughness

載荷為2 MPa 時，模型M1.6-R3.2 中橡膠材料的接觸應力和總變形如圖13 所示。接觸應力集中分布在微凸體的凸起或凹谷中，較大的變形則多發生在凸起的地方。結合粘著接觸狀態可以想象，兩個微凸體在外加載荷作用下相互嚙合，粘結在一起，由于應力集中，較軟一方的微凸體產生大變形而被撕裂，脫落成為磨粒。因此，界面間發生粘著接觸的范圍決定著磨損界面磨粒的分布范圍。

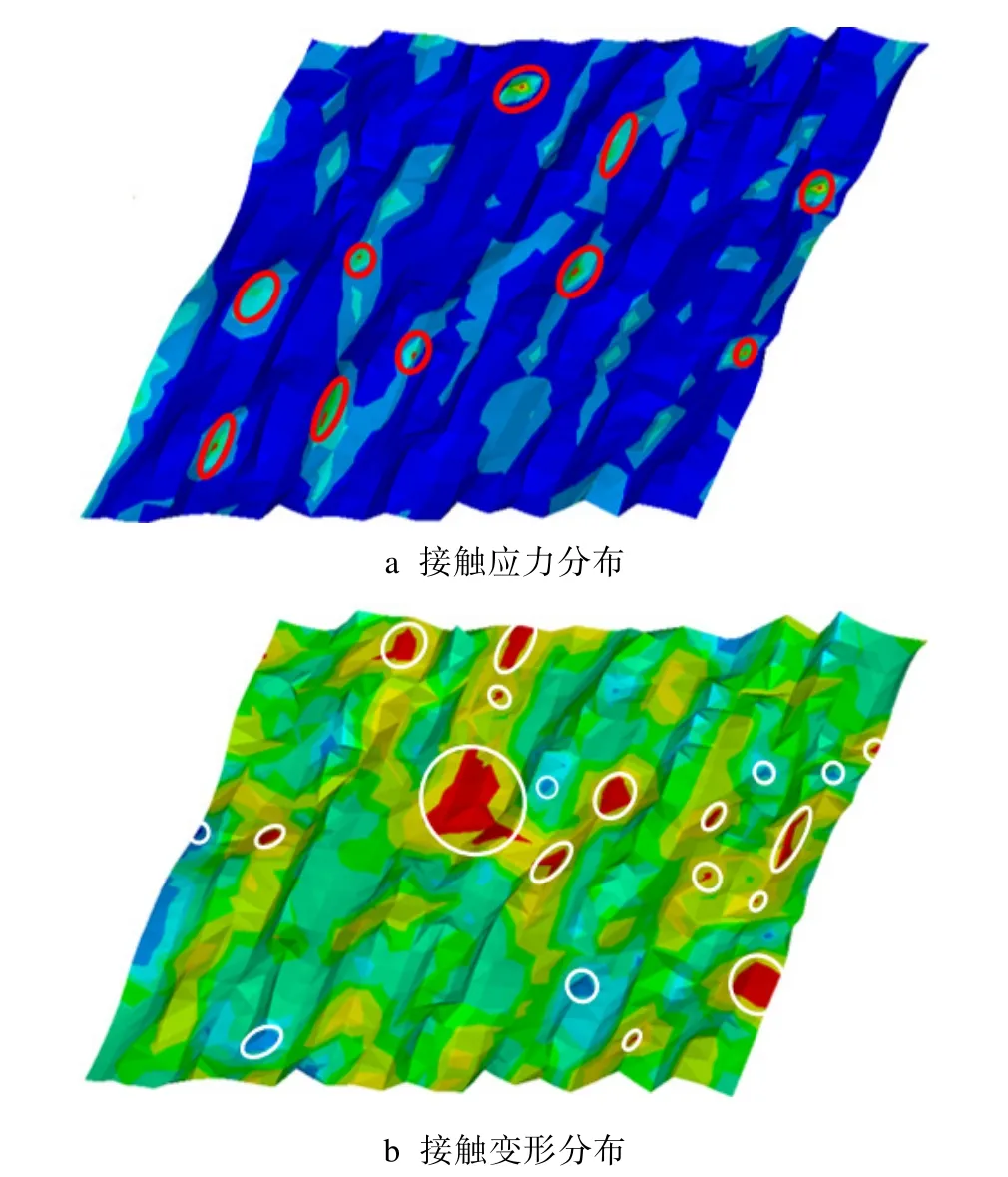
圖13 橡膠的接觸應力和總變形分布Fig.13 Distribution of contact stress and total deformation of rubber: a) distribution of contact stress; b) distribution of large deformation

通過接觸面積確定兩個粗糙面間因分子間相互作用而產生的范德華力的分布范圍，突破了僅考慮高度分布的高斯分布的局限性，進一步解釋了粘著接觸導致界面間磨損粒子大小改變的機理，這對于準確描述載荷傳遞和隨之發生的磨損過程有著重要意義。在外加載荷作用下，產生接觸的微凸體數量增加，兩個粗糙表面發生粘著的微凸體數量隨之增加。在發生錯峰滑移之前，微凸體上的應力遠超其強度極限，在金屬-橡膠接觸中，橡膠的相對硬度很小，橡膠微凸體被撕裂并脫落成磨損顆粒。上述行為再次驗證了磨粒磨損是金屬-橡膠剛柔接觸界面的主要磨損形式。

4 結論

本文針對金屬-橡膠變形接觸問題，從微觀角度出發，提出了橡膠接觸面粗糙峰坐標點云重構的方法，實現了對金屬-橡膠“剛柔”接觸的分析，得出以下結論：

1）隨著外加載荷的增加，界面真實接觸面積呈非線性增加，對不同粗糙度的接觸表面，接觸面積隨載荷的變化趨勢基本一致。在同一載荷下，真實接觸面積隨粗糙度的增加而減小；當載荷足夠大時，接觸面積會隨著表面粗糙度的增加而增加，且增加趨勢顯著。

2）初始接觸時，界面間的接觸狀態以近場接觸為主，隨著外加載荷的增加，近場接觸向粘著接觸轉變，在整個接觸過程中，滑移接觸的占比較為穩定。

3）在金屬-橡膠接觸中，接觸面積和接觸狀態共同決定了接觸界面間產生的磨粒大小及分布范圍，其中，接觸狀態起主要作用。從橡膠的應力分布和變形情況可以看出，橡膠表面的微凸體更容易脫落而形成磨粒，證明磨粒磨損是金屬-橡膠接觸界面的主要磨損形式。