基于模糊卡爾曼濾波車速估算的泊車運動學模型

王 龍，李紅娟

(西安航空學院 a.車輛工程學院；b.汽車檢測工程技術中心， 西安 710077)

未來汽車的主要發展方向之一是智能化，自動泊車系統作為智能汽車的重要組成部分，越來越多地受到來自科研機構和汽車廠家的關注[1]。

目前，科研機構對自動泊車技術的研究主要是在車位智能快捷識別、自動泊車路徑規劃、泊車運動跟蹤及控制等。在車位智能快捷識別的研究中，文獻[1-3]主要通過距離和視覺信息融合對停車位進行智能識別。這些泊車車位智能快捷識別對泊車的運動學因素均有考慮，但并未對泊車運動學模型的建立做深入的研究。

在自動泊車的路徑規劃與運動控制研究中，文獻[4]解決多車泊車路徑規劃問題，文獻[5]提出了一種基于優化狹窄環境下的停車場路徑規劃方法。此外，還有其他文獻的泊車路徑規劃[6-8]，而目前缺乏基于自動泊車自身特點的專用泊車運動學模型。文獻[9]提出了一種基于坐標補償的自動泊車系統無模型自適應控制。文獻[10]提出了一種基于機器視覺和模糊控制的自動泊車系統。其他的文獻還有利用卡爾曼濾波控制、自適應控制以及神經網絡算法和智能算法[11-14]等控制方法來解決泊車運動跟蹤及控制問題。自動泊車的路徑規劃與運動控制研究的前提就是建立泊車的運動學模型，但這些泊車運動學模型主要基于1989年J.P.Laumond and T.Simeon中提出的簡化汽車運動學模型，缺乏基于自動泊車自身特點的專用泊車運動學模型理論及驗證實驗。

自動泊車的運動過程是一種非完整鏈式系統[15]，具有非線性、時變、多變量等特點，很難建立起準確的非完整鏈式自動泊車模型，但可以通過對模型相關因素的分析建立簡化的汽車運動學模型。此外，文獻[16]通過分析沒有主觀知識的最優控制問題，實現了基于時空分解的平行泊車運動優化策略，提供精確、客觀的車輛運動學模型，但其理論深奧，算法復雜，缺乏實車驗證。文獻[17]利用自動泊車的起始坐標位置或起始區域、車速、車身轉角、前輪轉角的實時數據建立簡化的汽車運動學模型，通過對速度誤差和車身轉角誤差的考慮建立模糊邏輯控制器，實現了較好的泊車效果，但對于狹小空間內的多次泊車超低速運動缺乏深入研究和實車驗證。

總之，泊車運動過程中的控制復雜，建立基于自動泊車自身特點的專用運動學模型十分重要。本文通過對相關文獻和實際泊車過程的分析，提出了一種基于模糊卡爾曼濾波車速估算的泊車運動學模型，符合泊車運動過程的要求，同時可以降低泊車運動過程中位移和航向角的計算誤差。

1 汽車簡化的泊車運動學模型

1989年，J.P.Laumond and T.Simeon提出了簡化的汽車運動學模型如圖1所示[18]。

在圖1中，建立全局坐標系xf，選取后軸中心M作為泊車車輛運動學模型的基點，M點坐標為(xf)，以后軸中心M為基準點，車輛低速運動學方程為：

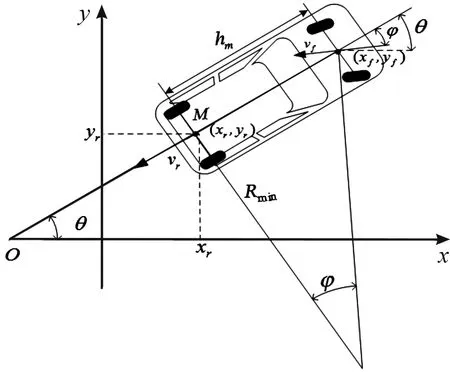
圖1 簡化的車輛運動學模型示意圖

(1)

其中，xf為前軸中心橫坐標；yf為前軸中心縱坐標；xr為后軸中心橫坐標；yr為后軸中心縱坐標；vr為后軸中心速度；vf為前軸中心速度；θ為航向角；φ為前軸中心轉角；hm為前后軸軸距；Rmin為最小轉彎半徑。

以后軸車速vr作為整車車速v，建立車輛運動學數學模型，如圖2所示。

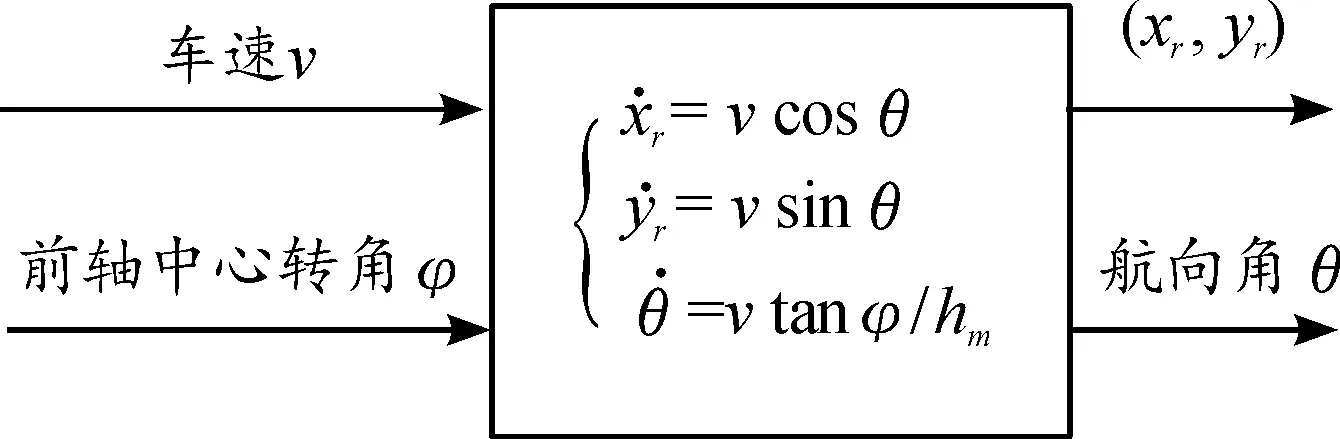
圖2 車輛運動學數學模型示意圖

2 泊車車速分析

通過對自動泊車運動過程的分析，車輛在超低速情況下對車速的測量存在局限性，高精度測量車速存在困難，建立的泊車運動學模型也不能準確反映泊車的過程。在泊車起步階段、中間階段、最后泊車結束階段都存在泊車車速測試偏差現象。在泊車中間階段，車速變化不大，這一過程主要是泊車的方向盤變化較大，引起前輪中心轉角變化增大，最終影響車輛的航向角和位置改變。針對這種情況，準確估算泊車起步階段和泊車結束階段的車速就顯得尤為重要。泊車過程測試的車速變化曲線，如圖3所示。

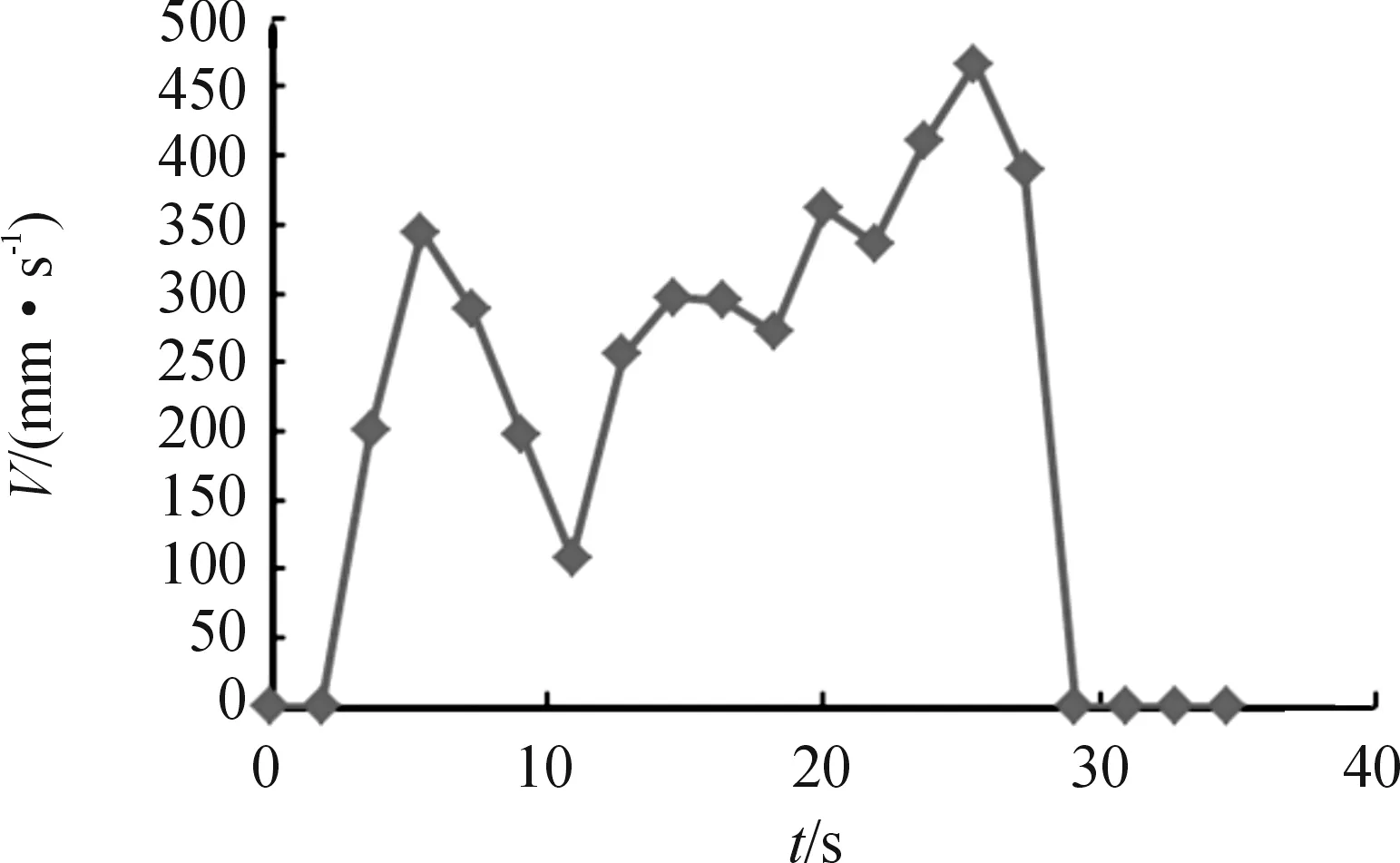
圖3 泊車過程測試的車速變化曲線

在泊車起步階段，車速從0到穩定車速，這一過程，前期是瞬時階段，中期是加速階段，后期車速趨于穩定。車速變化劇烈，時間在2～5 s內。對于具體車速要充分考慮前期的瞬時速度，中期加速階段變化，以及后期車位內調整車速。在泊車結束階段，車速從高速變為0，這一階段車速變化劇烈，時間在4～12 s內，且有一部分車速無法測試出來。對于具體車速的估算要充分考慮泊車過程中超聲波傳感器的工作過程，車速傳感器的精度，以及駕駛員的反應時間等因素。整體上而言，泊車過程考慮因素較多，比較復雜，因此通過車輪轉動速度的測量估算車速不能準確反映泊車運動過程中車速的變化。

3 泊車車速估算的算法原理

3.1 泊車車速測量方法

泊車車速可以通過車輪轉動圈數(車輪滾動距離)及轉動時間的測量，通過簡單計算得到，易于實現，當車輪打滑或輪胎不斷磨損時，會造成測量精度有較大誤差。

泊車車速也可以通過10軸加速度傳感器JY-901B(加速度計，如圖4所示)測量加速度值積分后得到車速。將4個相同的10軸加速度傳感器JY-901B分別安裝在車輛4個車輪中心，通過對相關數據的解析，得到泊車車速，即加速度積分可得到車速。

圖4 加速度傳感器JY-901B實物圖

綜上，車輪轉動速度測得的車速易受車輪側偏和車身慣性的影響(甚至在某些情況下傳感器通訊傳輸丟碼)。車身加速度積分所得車速對于安裝位置較敏感且存在誤差累積。由于單一的算法會造成較大的誤差，本文通過對相關文獻的分析，建立了一種將測量車輪轉動速度與車身加速度積分所得車速進行模糊卡爾曼濾波融合得到泊車不同階段的車速估算值[19]。

3.2 泊車車速估算結構

首先，分別用車輪轉動(取后輪兩車速均值)和加速度的方法(四輪主要取后輪兩加速度均值，也可適量考慮前后軸動力分配來調整四輪加速度加權值)測量車速和加速度值；然后將得到的數據利用卡爾曼濾波算法進行融合，去掉各傳感器帶來的測量噪聲，同時考慮累積誤差[20]；再根據泊車的不同狀況，利用模糊算法確定速度和加速度的權重充分進行濾波處理。圖5所示為泊車車速估算結構。

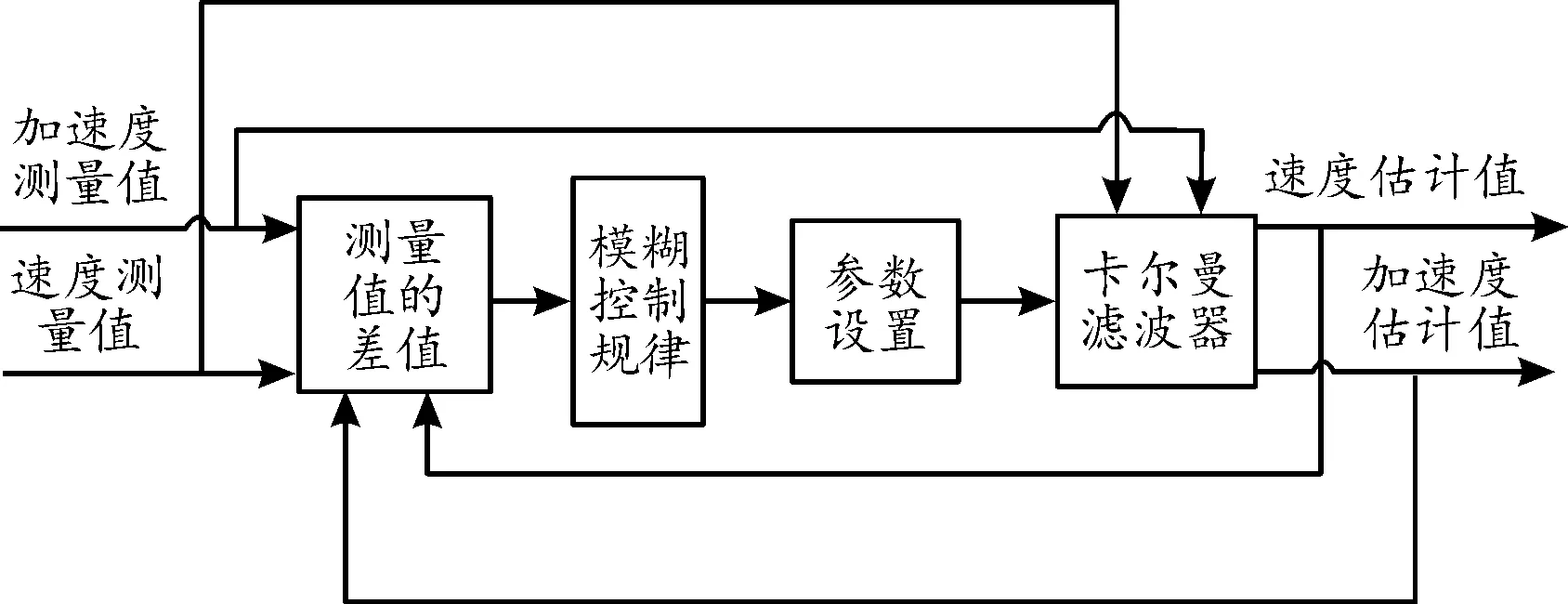
圖5 泊車車速估算結構框圖

3.3 泊車車速估算的算法設計

泊車車輪在啟動和停止過程中的慣性力量、車輪的擠壓形變甚至磨損均會對泊車車速產生影響，那么泊車車速的真實值、測量值、估算值之間會存在一定的函數關系。加速度也有類似關系。

νt=νg(1+α)

(2)

νc=νt+nν

(3)

ac=at+na

(4)

式中：vt為速度的真實值；vg為速度的估算值；vc為速度的測量值；nv為速度測量時的測量噪聲；at為加速度的真實值；ac為加速度的測量值；na為加速度測量時的測量噪聲。

在此假設nv與na為均值為0的高斯白噪聲。同時，定義加速度的變化率wa和速度的變化率wv。

(5)

(6)

偏移量的變化率為

(7)

將其代入卡爾曼濾波的離散化方程為：

X(k+1)=A(k)X(k)+B(K)ω(k)

(8)

Z(k)=CX(k)+N(k)

(9)

式中：參數分別為

(10)

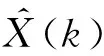
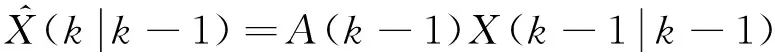
(11)

協方差的上一個狀態方程：

(12)

卡爾曼濾波增益方程：

(13)

卡爾曼濾波估計方程：

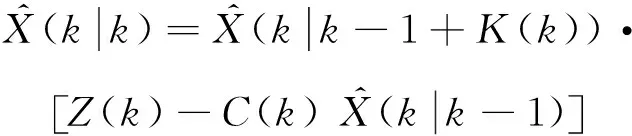
(14)

卡爾曼濾波協方差更新方程：

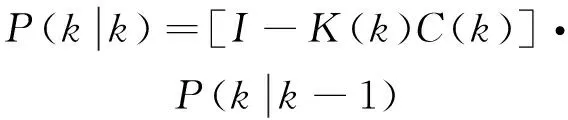
(15)

泊車運動過程中車速的變化幅度較大，固定參數的卡爾曼濾波器可以過濾掉一部分測量誤差，但是估算的車速離真實值有較大偏差，不能很好地反映泊車過程中的真實車速。尤其是泊車起始和結束階段，速度變化值較快，測量的速度值與真實值偏離較大，此時需要根據加速度值的算法估算真實車速。在泊車過程中，速度測量值與真實車速比較接近，所以應加大速度值的權重進行泊車車速估算。

模糊控制器的輸入量分別為估計值與測量值的絕對差值，即：

(16)

模糊控制的輸出量協方差矩陣R=(Rν，Ra)，即噪聲協方差矩陣R由速度和加速度測量的協方差組成。可以通過改變噪聲協方差矩陣R的值改變測量速度與加速度值的權重，從而得到準確的泊車車速估算值。泊車車速v的取值區域為[0，0.5]m/s，泊車加速度a的取值區域為[0，0.6]m/s2，車速協方差Rν的取值區域為[0，0.2]，加速度協方差Ra的取值區域為[0，0.4]，輸入輸出隸屬度函數如圖6～9所示。根據泊車實際實驗建立模糊規則表，如表1、2所示。

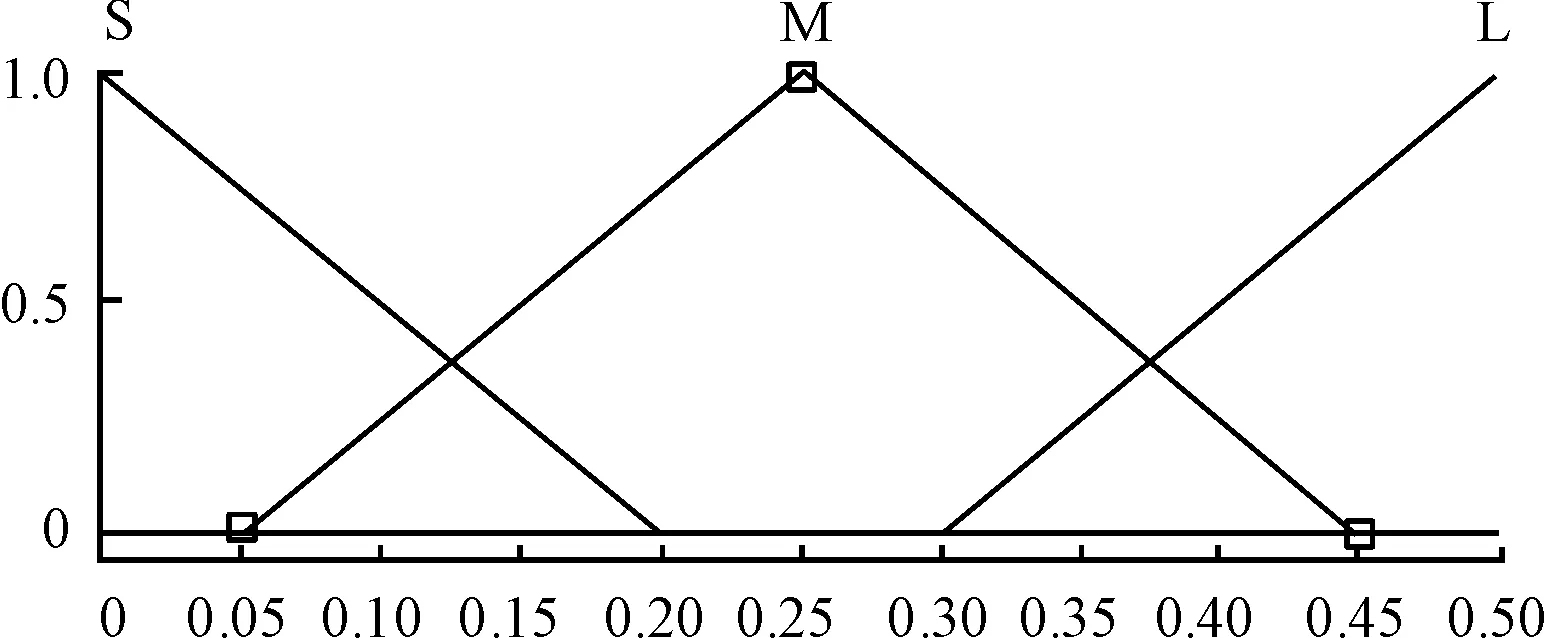
圖6 輸入變量泊車車速v的隸屬度函數曲線

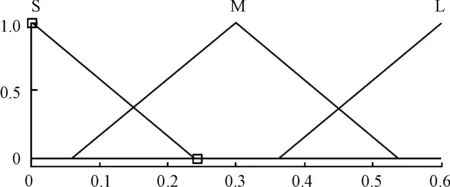
圖7 輸入變量泊車加速度a的隸屬度函數曲線

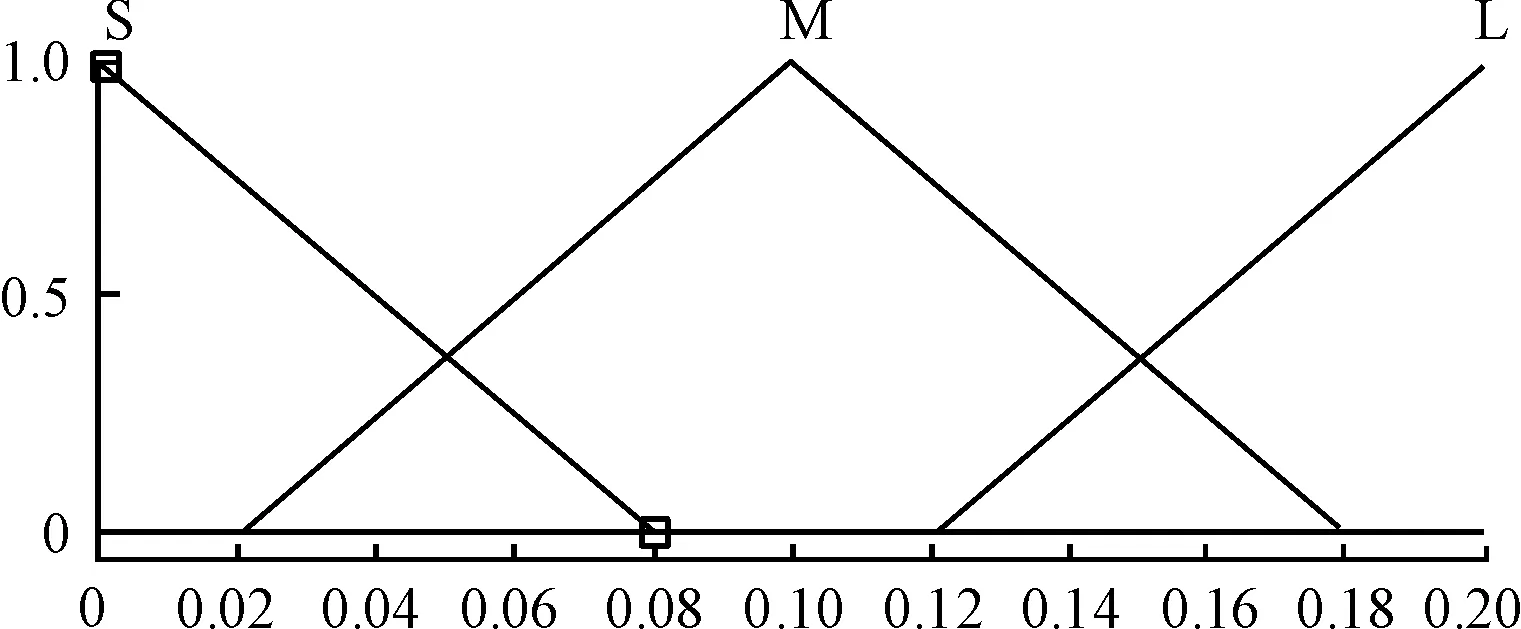
圖8 輸出變量車速協方差Rν的隸屬度函數曲線

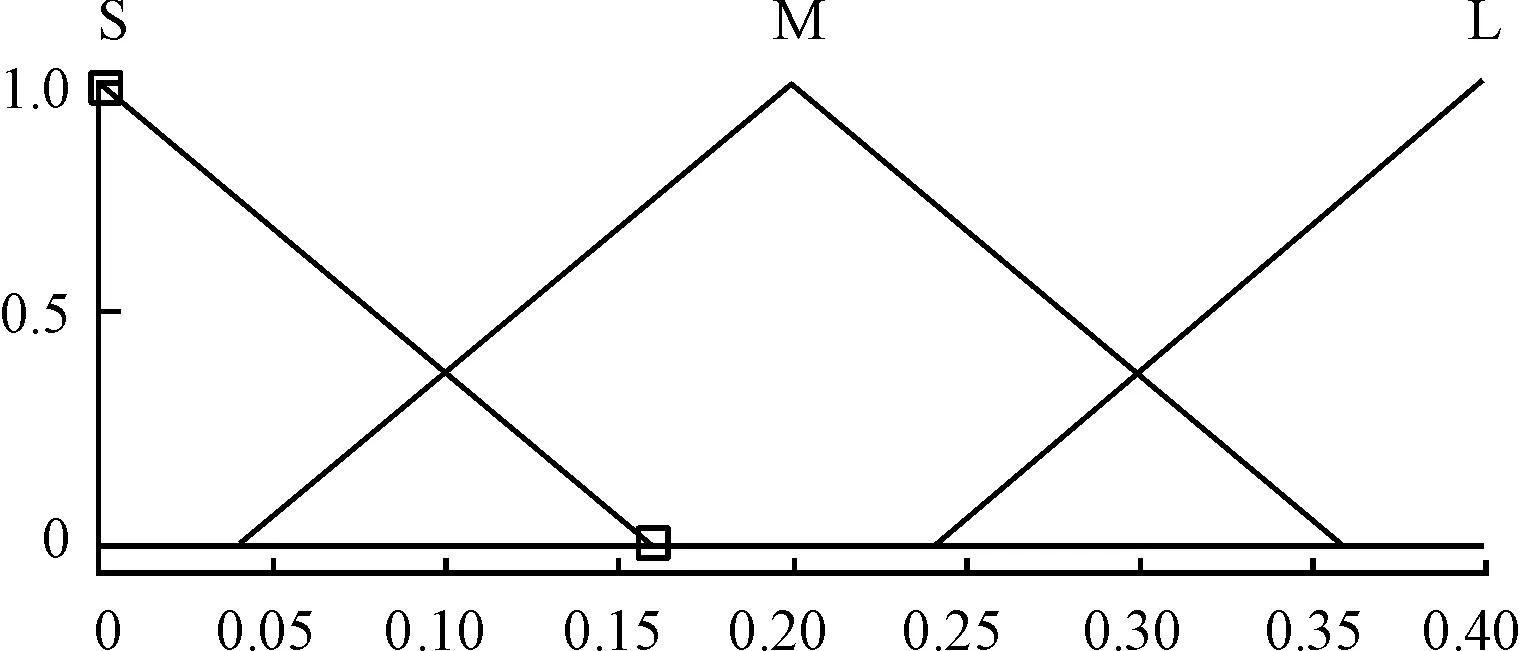
圖9 輸出變量泊車加速度協方差Ra的隸屬度函數曲線

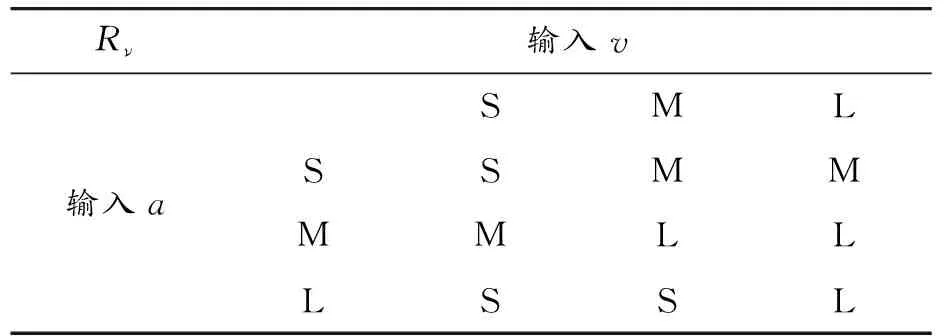
表1 Rν的模糊規則

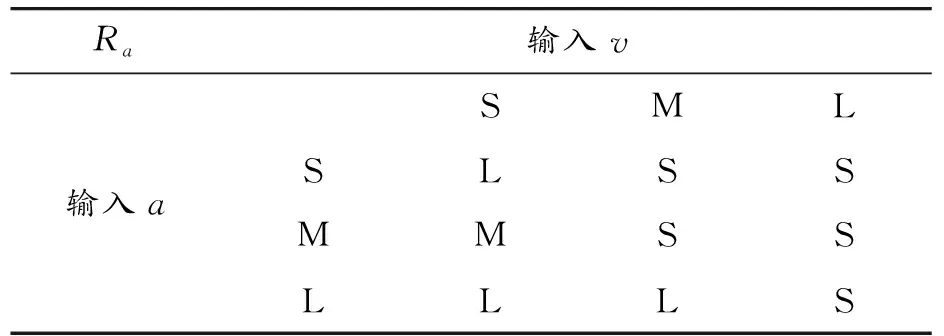
表2 Ra的模糊規則

表中S、M、L分別代表模糊子集的小、中、大，邏輯關系主要代表泊車過程中的運動情況。

1) 在泊車的起始過程中，車輛速度很低，加速度較大，加速度測量誤差較小。由于車身的重量具有一定的慣性，車輪的車速值較小，測量誤差較大。即a= L，v= S，此時應提高加速度測量值的權重，減小速度測量值的權重。

2) 在泊車的中間階段、轉動角度變化不大的過程中，車輛保持低速運動，此時車輪的加速度和車速測量誤差都較小。即a=S，v=S，此時應提高泊車速度測量值的權重，減小加速度測量值的權重。

3) 在泊車的中間階段、轉動角度變化較大的過程中，車輛保持低速運動，此時車輪的加速度和車速測量誤差均較大。即a=L，v=L，此時應提高泊車加速度測量值的權重。

4) 在泊車的中間階段、轉動角度變化適度的過程中，車輛保持低速運動，此時車輪的加速度和車速測量誤差一般大。即a=M，v=M，此時應提高泊車速度測量值的權重。

5) 在泊車的中間階段、換前后擋的過程中，車輛保持低速運動，此時車輪的加速度誤差較大，泊車車速測量誤差一般。即a=L，v=M，此時應提高泊車速度測量值的權重。

6) 在泊車停止階段的過程中，車輛保持超低速運動，泊車車速測量誤差較大。此時a=M，v=L，應增加泊車加速度測量值的權重。

最后，對模糊算法進行反模糊化求解，確定測量噪聲的協方差矩陣R。

3.4 泊車車速估算的仿真

將圖3中的泊車過程數據進行車速估算仿真，根據速度估算值代入式(1)中進行泊車過程的仿真。泊車車速估算的仿真過程如圖10所示。泊車過程車速估算結果如圖11所示。泊車實驗測得前輪轉角如圖12所示。

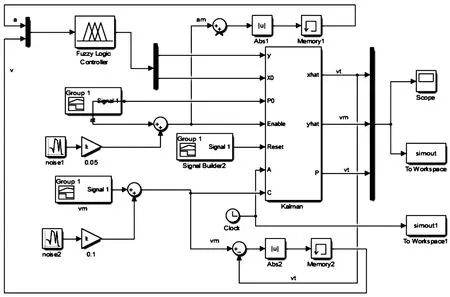
圖10 泊車車速估算仿真過程框圖

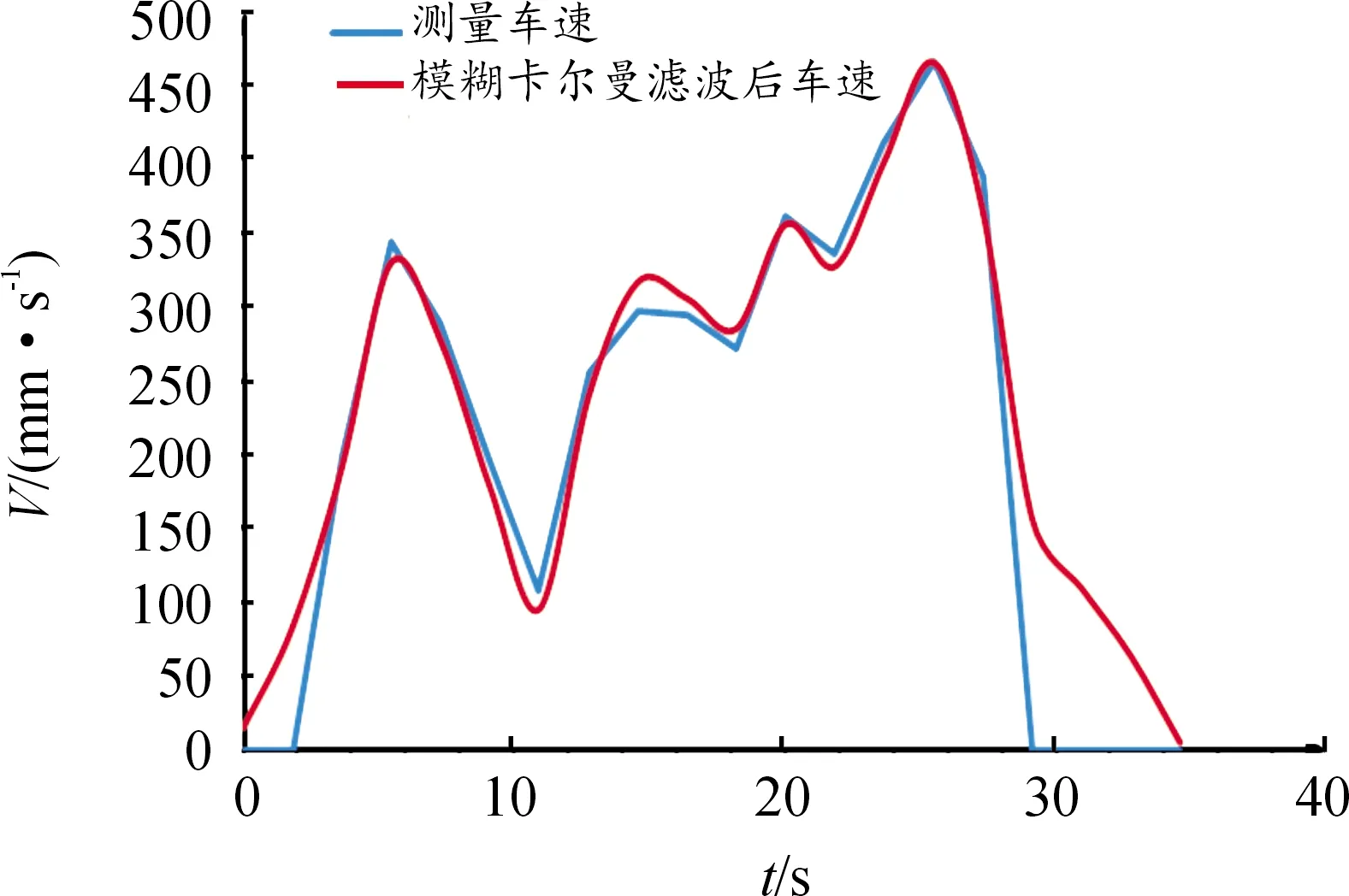
圖11 泊車過程車速估算結果

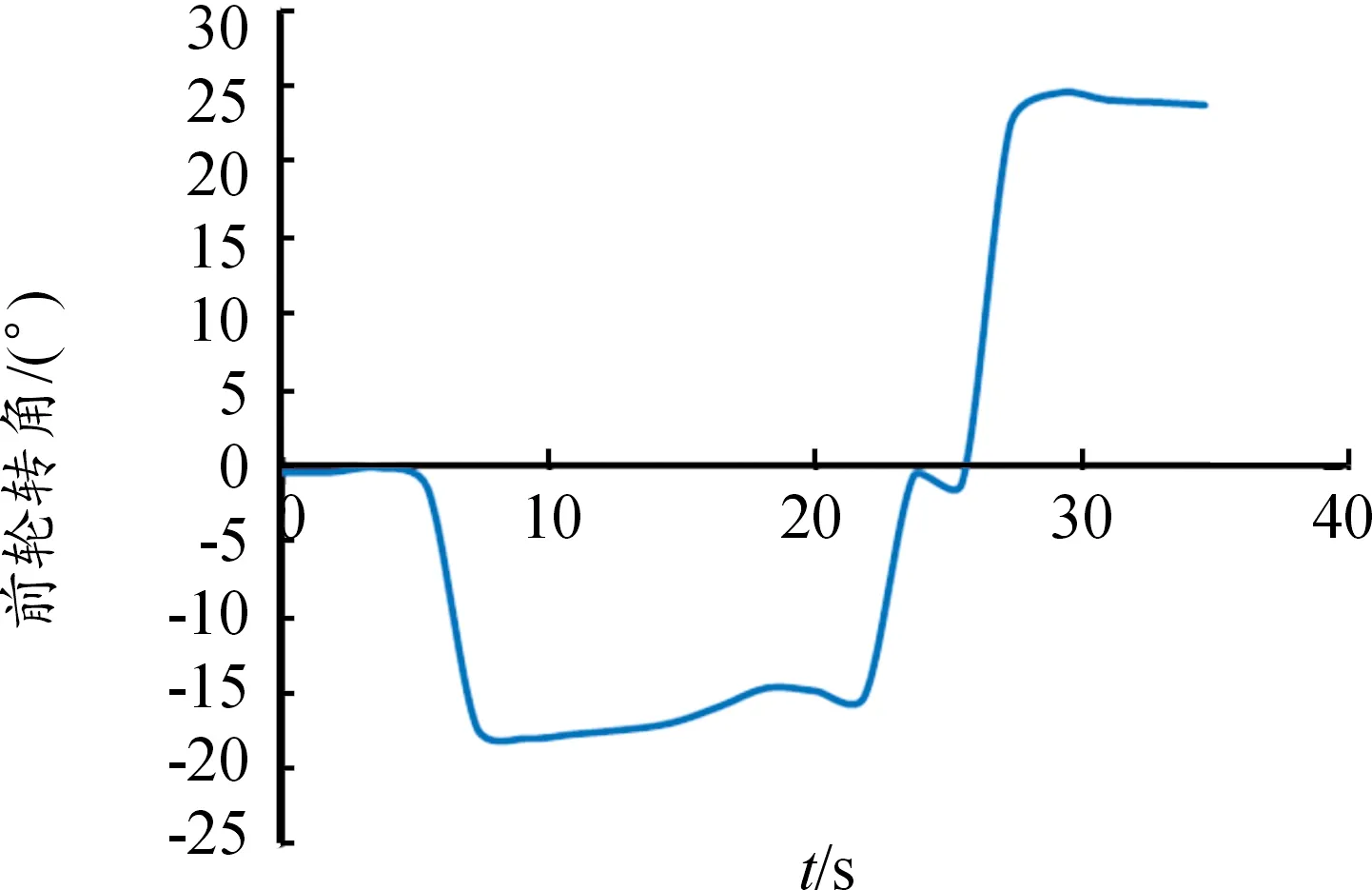
圖12 泊車過程前輪轉角

3.5 泊車運動simulink仿真模型

通過建模式(1)，得到泊車運動仿真時的姿態信息[21]。圖13所示即為Simulink中搭建的泊車車輛運動學模型。

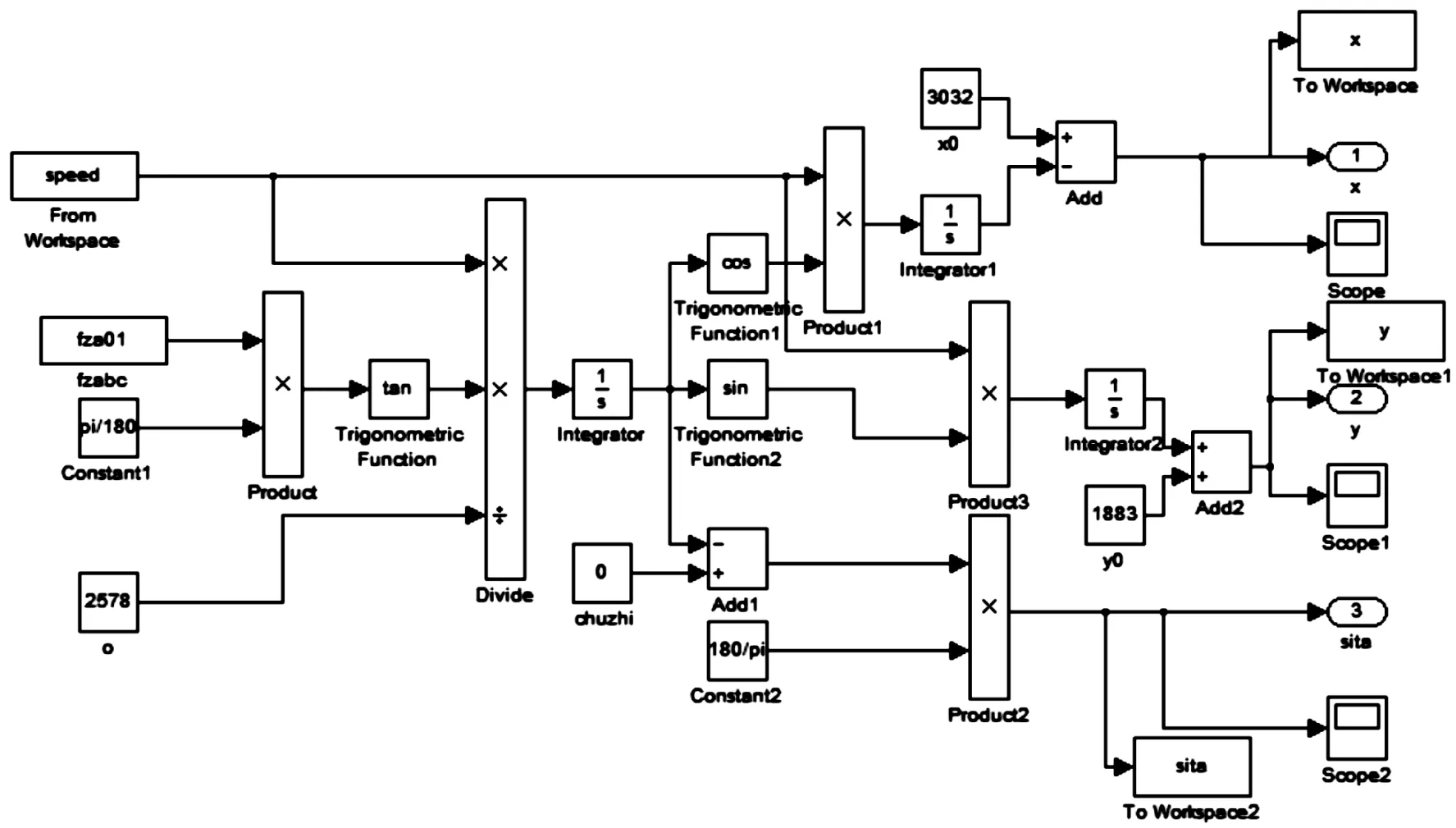
圖13 Simulink搭建泊車車輛運動學模型框圖

3.6 泊車實際坐標與仿真模型的比較分析

通過Matlab的繪圖功能，得到估算車速的泊車模型、原有泊車模型以及實際泊車航向角，如圖14所示。橫坐標X對比，如圖15所示。縱坐標Y對比，如圖16所示。

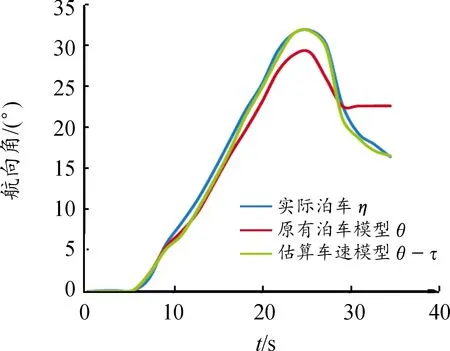
圖14 3種泊車運動學模型航向角

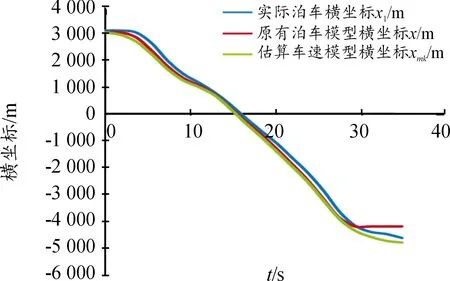
圖15 3種泊車運動學模型橫坐標X

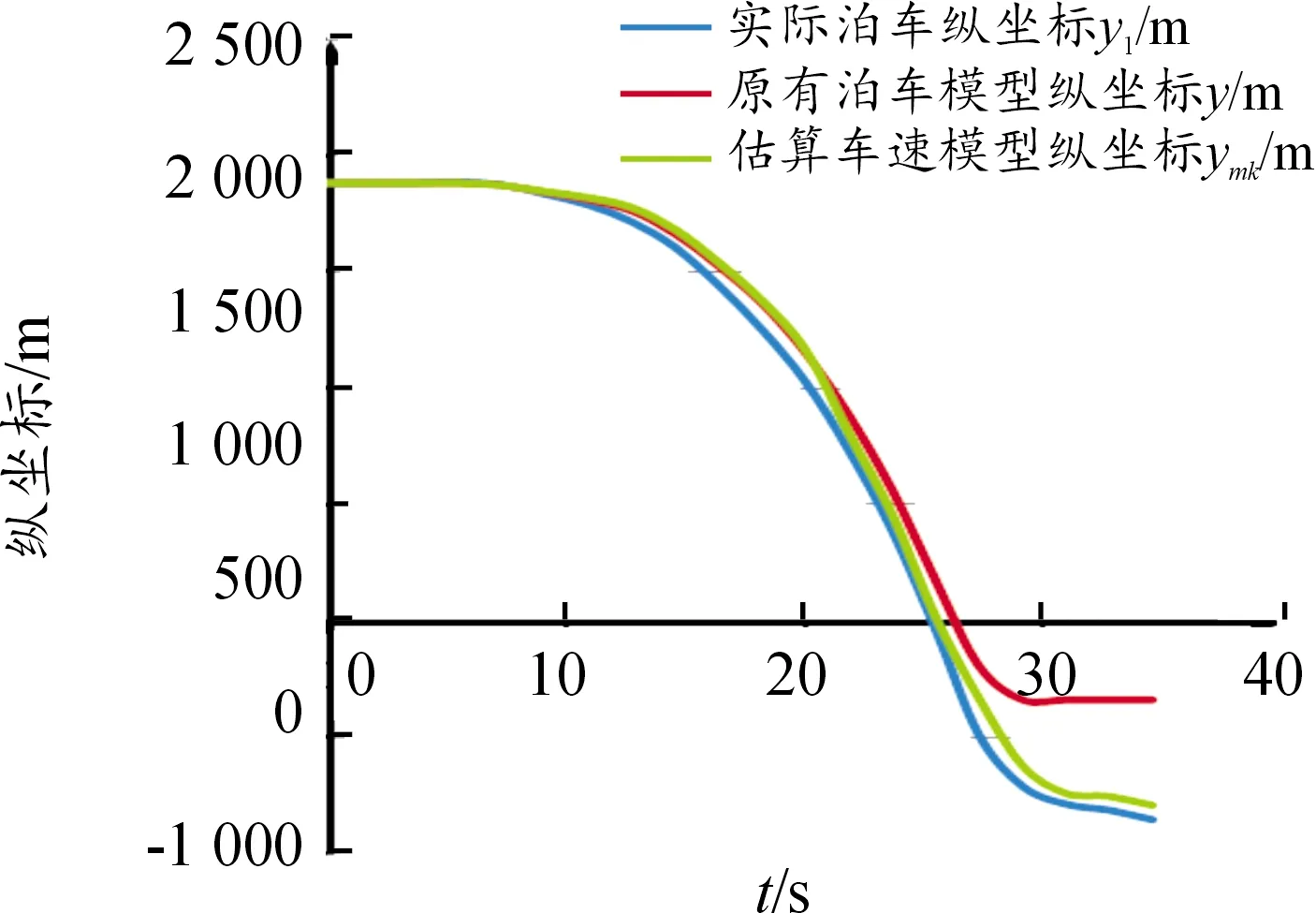
圖16 3種泊車運動學模型縱坐標Y

由圖14可知：在泊車中期和末期，仿真曲線中原有泊車模型的航向角與實際泊車差距較大，主要由于車速測量不準確造成。原有泊車模型航向角的偏差為[-4.2°，6.5°]，最大誤差率為0.39°。車速估算后的車輛航向角偏差為[-3°，0.5°]，最大誤差率為0.09。車速估算使得泊車末期的航向角整體趨勢更接近實際測量值，誤差率降低了30%。

由圖15可知：原有泊車模型與實際泊車位移橫坐標偏差為[-450 mm，50 mm]，最大誤差率為0.09。估算車速的泊車模型與實際泊車橫坐標的最大位移偏差為153 mm，最大誤差率為0.03。誤差率下降了6%。

由圖16可知：泊車前期和泊車中期，估算車速的泊車模型、原有泊車模型與實際泊車縱坐標吻合度較高。通過計算，前期和中期的最大Y位移偏差為[0 mm，490 mm]，最大誤差率為0.05。而后期的誤差率大是由于車速測量不準確引起的，原有泊車模型與實際泊車縱坐標后期的最大位移偏差為490 mm，最大誤差率為0.14。估算車速的泊車模型與實際泊車縱坐標最大位移偏差為48 mm。最大誤差率為0.05，降低了9%。驗證了合理的車速估算可以極大地降低因車速測量不準確導致的仿真誤差。

本文中所設計的模糊卡爾曼濾波能更好地處理實際泊車工況下的車速估計問題，所采用的模糊卡爾曼濾波相較普通卡爾曼濾波在估計車速上優勢明顯，更接近實際泊車情況。模糊卡爾曼估算車速的泊車模型、普通卡爾曼泊車模型以及實際泊車航向角如圖17所示。橫坐標X如圖18所示。縱坐標Y如圖19所示。

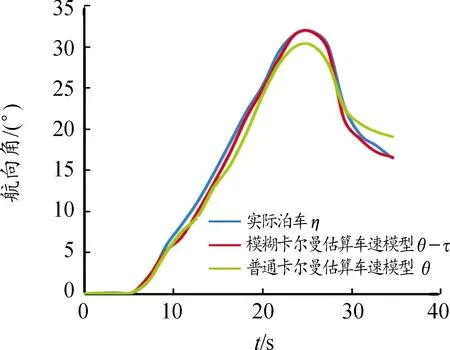
圖17 3種泊車運動學模型航向角

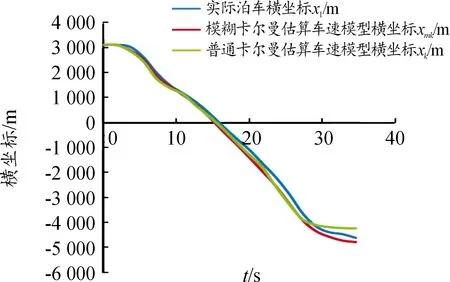
圖18 3種泊車運動學模型橫坐標X

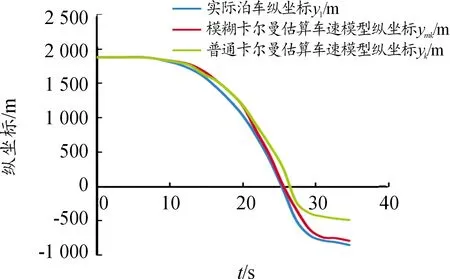
圖19 3種泊車運動學模型縱坐標Y

經Matlab/simulink仿真和泊車實驗的數據對比分析結果表明：建立的基于模糊卡爾曼濾波車速估算的泊車運動學模型與原泊車運動學模型相比在精度上提高了15%，與實際泊車情況偏差3%。

4 結論

針對自動泊車運動過程中的自身特點，提出了一種基于模糊卡爾曼濾波車速估算的泊車運動學模型，符合泊車運動過程的要求。從3種泊車運動學模型實驗分析對比可得模糊卡爾曼濾波估算車速的泊車模型與實際泊車結果基本吻合，誤差值在可接受范圍之內。該估算車速的泊車模型符合車輛低速泊車時的運動規律要求，降低了泊車整個過程的位移和航向角計算誤差，對于進一步研究泊車路徑規劃與控制具有重要意義。