具有三維Keller-Segel趨化模型古典解的存在性

胡 巧 玲

(電子科技大學 數學科學學院， 四川 成都 611731)

0 引言

趨化是生物領域中的常見現象，常見于種群入侵，物種繁殖，癌細胞的發現等.趨化模型主要用于描述細胞聚合現象，即在化學物質的吸引下，細胞會在有限時間內發生聚集或是細胞的數量在某一時刻會趨于穩定.早在20世紀70年代，Keller和Segel就提出細胞遷移的趨化模型，即Keller-Segel模型，他們發現除了細胞的隨機擴散運動，細胞會朝向化學物質濃度高的地方,由此得到如下的趨化模型[1]

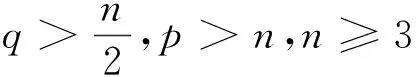
一般地，對于結構更為簡單的有機物也會朝著消耗營養物的方向進行遷徙，故得到如下趨化模型

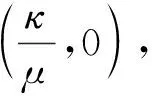
Fuest[9]運用Schauder估計得到了如下帶諾依曼邊值條件趨化模型解的正則性結果以及解的長時間行為

(1)

這里，Ω是一個有界的光滑凸區域，δ>0是一個給定的參數，(u0,v0,w0)是給定的初值并且滿足

(2)

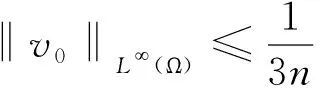
基于以上結果，本文研究在三維情況下帶間接信號消耗的趨化系統(1)的正則化模型

(3)

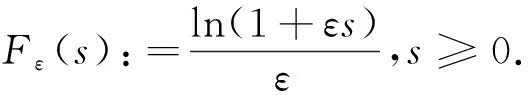
本文的主要結果是利用Banach不動點定理證明了系統(1)古典解的整體存在性以及系統(1)的正則化系統(3)的弱解存在性. 具體表述如下：

定理1若系統(3)的初值(u0,v0,w0)滿足(2)式，則對任意的ε∈(0,1),系統(3)存在唯一的整體古典非負解(uε,vε,wε) ,并且存在序列(εj)j∈Ν?(0,1),εj→0,滿足

uε→u;vε→v;wε→w,

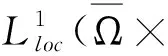
1 預備知識

定義1稱(u,v,w)是系統(1)的弱解是指函數(u,v,w)滿足

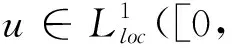
2 主要結果

定理2若系統(3)的初值(u0,v0,w0)滿足(2)式，則對任意的ε∈(0,1),系統(3)存在唯一的整體古典非負解(uε,vε,wε).

證明存在性

取定R>0是一個常數以及T∈(0,1),考慮Banach空間

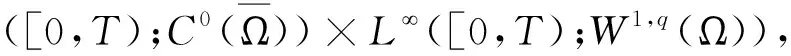
其中q>3.考慮閉集

S:={(uε,vε)∈X|‖uε(·,t)‖L∞(Ω)+‖vε(·,t)‖W1,q(Ω)≤R,t∈(0,T)}

.

令Φ=(Φ1,Φ2)作用在S上，并且定義

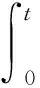
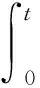
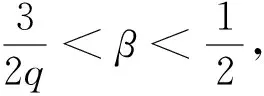
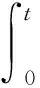
(4)

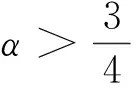
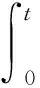
(5)

其中，C4,C5,C6(R),C7(R)都為大于0的常數.結合(4-5)式就可以……