具有收獲率和Holling-Ⅱ型功能反應函數的時滯系統的定性分析
2021-11-05 05:08:22姚佳佳
內江師范學院學報
2021年10期
關鍵詞:系統
沈 維, 姚佳佳
(蘭州交通大學 數學系, 甘肅 蘭州 730070)
0 引言
在生物數學中食餌-捕食模型作為重要的動力系統,近年來引起了許多研究者的廣泛關注.在動力學研究中,穩定性與分支現象一直都是一個熱點問題,從最初模型的建立到后來的廣泛研究,數學家和生物學家致力于更準確地描述捕食者-食餌系統中存在的動態行為.為了體現捕食系統的復雜性與現實性,學者們還將功能反應函數引入系統中去.
2017年,Hu和Li[1]基于捕食模型
(1)
提出了以下具有時滯和Holling-Ⅱ型功能反應函數的捕食系統
(2)
其中變量和參數的實際意義見文獻[1].他們主要研究了τj(j=1,2)的不同取值對正平衡點穩定性的影響.張宏民等[2]研究了以下具有收獲率的Holling-Ⅱ類功能反應系統
(3)
其中F,G分別表示人們對食餌和捕食者的捕撈程度.他們主要對該常微系統進行了平衡點的穩定性分析.
2021年,Wang等[3]討論了具有時滯和Holling-Ⅲ型功能反應的食餌-捕食系統
(4)
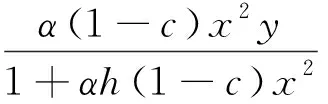
基于系統(2)和(3),本文將研究以下具有收獲率的Holling-Ⅱ型功能反應的時滯食餌-捕食系統
(5)
通過詳細分析系統(5)在正平衡點E*(u*,v*)線性化系統的特征方程來探究系統正平衡點的穩定性與Hopf分支.u,v分別表示食餌與捕食者的種群數量,參量意義參考文獻[1,3].τ表示食餌的生產時滯.
1 無時滯系統的穩定性和Hopf分支
在τ=0時,系統(5)變為
(6)
由文獻[1,4-5]可得以下結論:
引理1系統(6)的所有解都是非負的.
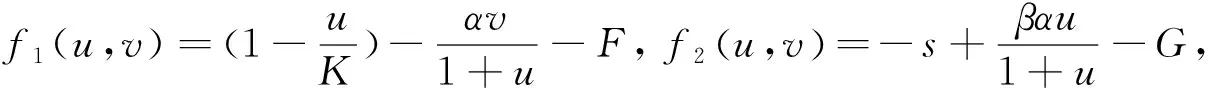
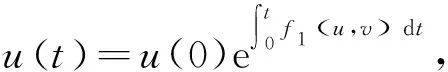
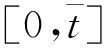
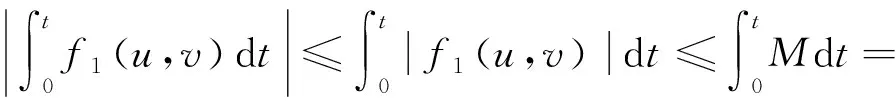
從而有
于是
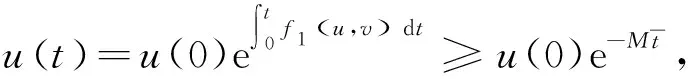
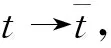
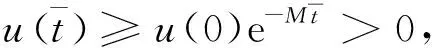
與假設矛盾,因此系統(6)的所有解都是非負的.
假設條件(B)1-F>0,βα>s+G且s+G 下面討論常微系統(6)在平衡點的穩……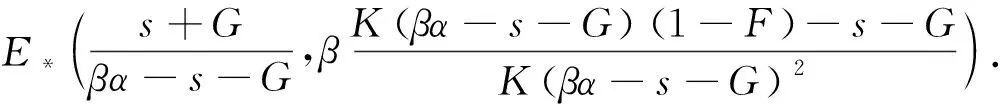 登錄APP查看全文
登錄APP查看全文
猜你喜歡
工業設計(2022年8期)2022-09-09 07:43:20
軍民兩用技術與產品(2021年10期)2021-03-16 06:05:30
北京測繪(2020年12期)2020-12-29 01:33:58
裝備制造技術(2019年12期)2019-12-25 03:06:46
制造技術與機床(2019年10期)2019-10-26 02:47:06
中國洗滌用品工業(2019年4期)2019-05-11 09:27:34
鐵道通信信號(2018年5期)2018-06-28 03:06:24
家庭影院技術(2017年9期)2017-09-26 03:41:45
通信電源技術(2016年6期)2016-04-20 06:21:32
智能系統學報(2015年4期)2015-12-27 09:37:59

