瀝青路面結構的疲勞損傷和壽命估算研究

□□ 王曉峰

(太原市市政公用工程質量安全站(太原市軌道交通建設服務中心)，山西 太原 030024)

引言

隨著科技的進步和經濟的發展，城市交通工具開始大量普及，市政道路工程的建設也大幅增加。市政道路工程具有系統性，瀝青路面鋪設是整個路面施工流程中的重要環節之一，其施工質量將對市政道路整體運行效果具有直接的影響，關乎行車舒適性與安全性。

本文以太原市某市政道路瀝青混凝土路面為例，該雙幅路雙向四車道路全長為7.3 km，路基寬度為6.5 m，路面側帶寬度分別為3.5 m，隔離帶的寬度為3.0 m，設計速度為40 km/h。該瀝青主路面結構層為：180 mm的瀝青面層、5 mm的瀝青封層、350 mm的泥穩碎石基層、200 mm的泥穩碎石底基層、200 mm的碎石墊層組成。面層由上、中、下三個層組成，其中上面層為40 mm橡膠瀝青細粒式混凝土(ARAC-13G)；中面層為60 mm中粒式改性瀝青混凝土(AC-20C)；下面層為80 mm粗粒式瀝青混凝土(AC-25C)，工程需瀝青混合料約18萬t。

1 瀝青路面常見的結構損傷問題

1.1 瀝青路面開裂

瀝青路面開裂是瀝青路面使用過程中較為常見的現象，瀝青路面開裂受多種因素的影響，因而路面開裂問題需根據具體情況分析。一般來說，瀝青路面開裂的原因分成兩個方面：首先是疲勞開裂。在路面受到外界交變載荷的擾動時，如反復溫度變化、反復的路面加載等，當路面承受的交變載荷達到極限，路面會產生疲勞，當疲勞反復疊加，則會產生路面開裂；其次是反射開裂。由于整個路面是由多層材料鋪設而成，而不同路面的結構參數與材料性能各不相同，這就導致路面在界面容易產生反射開裂。當某一層路面的位移產生的拉應力或者壓應力超過瀝青路面的抗拉強度或抗壓強度時，瀝青路面就會開裂，此時路面產生反射開裂。除了以上兩種開裂原因外，如果路面所使用的鋪設材料未達到路面的抗載荷要求，也會導致路面開裂。

1.2 瀝青路面車轍和沉陷

瀝青路面屬于柔性路面，大量車輛常年在路面行走，汽車不斷地對路面施加水平力和垂直力，導致路面形成了不可恢復的變形。同時，汽車輪胎與路面之間摩擦經過長時間的積累容易產生車轍。不可恢復的變形容易造成路面沉陷，這對于汽車的行駛存在極大的安全隱患。此外，造成路面沉陷的原因還有因路基不實而導致的路面蠕變。路基材料不穩定性的根本原因是施工質量未達到相關的技術要求。

1.3 瀝青路面凍脹和水損

對于北方的城市路面，瀝青路面的凍脹問題主要是在冬季。北方城市在入冬前都會有秋雨降臨，當降雨頻繁或者降水量驟增時，會導致大量的雨水不能及時排走，開始向路面下方滲透，這樣路面基層會儲存大量雨水；外界溫度下降時則會導致雨水開始結冰，這樣體積的急劇膨脹會導致路面開裂；到了春季冰的消融又導致路面出現翻漿現象。此外，消融的水經過汽車不斷碾壓會出現泵吸現象，從而加重了路面的破壞，所以路面的排水效率直接影響路面的長時間使用。

2 瀝青路面的線性損傷模型

基于多層彈性體系理論對瀝青路面結構進行損傷估算，在損傷估算前，先給出該線性損傷模型的基本假設，其表述如下：

(1)瀝青路面模型是基于多層彈性體系理論的，假設其在面內尺寸遠大于厚度方向，可認為該瀝青路面模型是基于平面應變假設的。根據平面應變假設的特點，分析截面可以選取車輛荷載中軸線的橫截面。

(2)多層瀝青路面中的各層材料模型可以假設為理想均質、各向同性、黏彈性的材料模型。

(3)假設土基厚度遠遠大于瀝青主路面結構層，瀝青主路面結構層各層的水平方向無限大。

(4)假設有向下的垂直路面均布車輛荷載(P=0.7 MPa)作用于多層瀝青路面。

一般來說，由兩種路面材料組成的路面模型的損傷因子D的取值范圍為[0,1]，但是在工程中，基層和底層的損傷模型不會一直滿足Miner線性疲勞損傷模型。因此，根據工程經驗可知，當路面損傷因子D=0.5時，此時材料已經發生破壞；當D>0.5時，材料已經發生損傷產生失效，后續過程已不再考慮。但不同于兩種路面材料組成的路面模型，瀝青路面屬于多層彈性體結構。基于Miner線性疲勞損傷理論，假設當基層的損傷因子D=0.75時，材料發生破壞，此時損傷因子D在[0，0.7]區間的基層結構可近似等價為彈性模量為400 MPa的級配碎石結構；忽略損傷因子D在[0.75,+∞]區間的損傷行為。

因此，根據Miner線性疲勞損傷模型，當損傷因子D=0.75時，基層中水泥穩定碎石降低為級配碎石(彈性模量為400 MPa)，此時假設瀝青路面的損傷不再繼續擴展。分別取ARAC-13G、AC-20C和AC-25C三種瀝青混凝土進行常應力小梁彎曲疲勞試驗，通過疲勞試驗數據建立每一種材料的應力-疲勞方程。在相同試驗條件下，對不同類型瀝青混凝土的應力-疲勞試驗數據進行線性回歸處理，得到了ARAC-13G、AC-20C和AC-25C三種瀝青混凝土的疲勞方程。

ARAC-13G瀝青混凝土的N-σ和N-σ/σmax的疲勞方程分別為：

lgNf=23.005-5.824lgσ

(1a)

lgNf=6.986-5.807(σ/σmax)

(1b)

AC-20C瀝青混凝土的N-σ和N-σ/σmax的疲勞方程分別為：

lgNf=22.854-5.889lgσ

(2a)

lgNf=7.115-6.979(σ/σmax)

(2b)

AC-25C瀝青混凝土的N-σ和N-σ/σmax的疲勞方程分別為：

lgNf=14.611-3.334lgσ

(3a)

lgNf=5.917-4.405(σ/σmax)

(3b)

ARAC-13G、AC-20C和AC-25C瀝青混凝土的N-σ和N-σ/σmax的疲勞方程如圖1和圖2所示。由圖1和圖2可知，ARAC-13G、AC-20C和AC-25C瀝青混凝土的應變-疲勞曲線均表現出較好的線性關系。應力水平對疲勞壽命有明顯的影響，隨著應力水平的升高，瀝青混凝土的疲勞壽命是逐漸降低的。圖1中三種瀝青混凝土疲勞曲線的斜率變化范圍較大，方程lgN=η-λlgσ中的λ取值范圍為3.34～5.12，η的取值范圍為14.62～20.20。圖2中三種瀝青混凝土疲勞曲線的斜率變化范圍較大，方程中lgN=η-λ(σ/σmax)中的λ取值范圍為4.41～6.98，λ值表明三種瀝青混凝土的疲勞性能對所施加應力的敏感程度有較大差別；η的取值范圍為5.92～7.12，這表明三種瀝青混凝土中AC-25C的抗疲勞性能最差，ARAC-13G的抗疲勞性能最好。

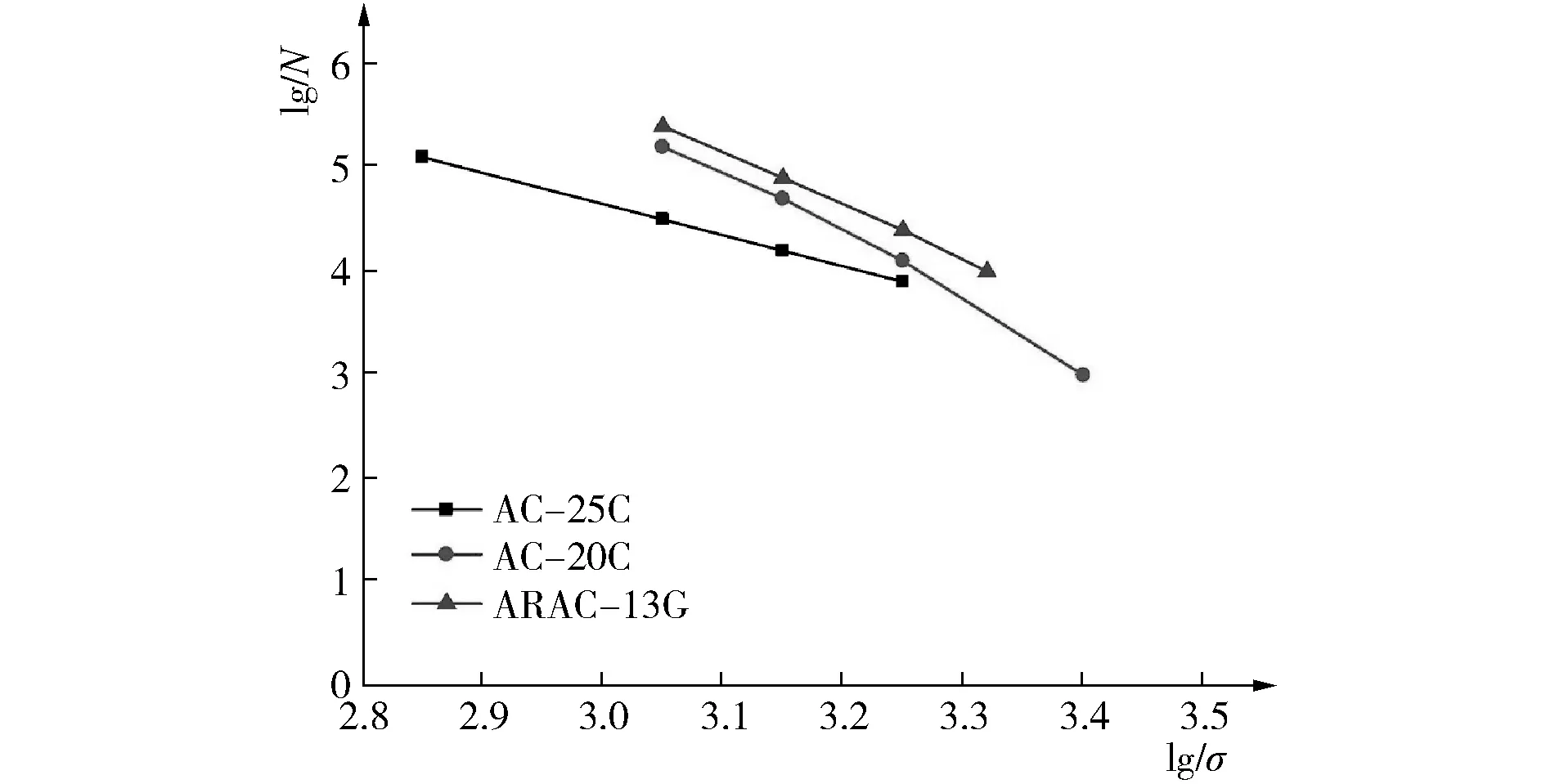
圖1 三種瀝青混凝土的N-σ疲勞方程

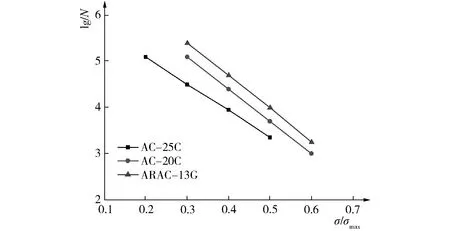
圖2 三種瀝青混凝土的N-σ/σmax疲勞方程

3 瀝青路面的結構損傷分析

該市政道路設計的路面結構層為ARAC-13G(40 mm)、AC-20C(60 mm)、AC-25C(80 mm)，基層為泥穩碎石基層(350 mm)、泥穩碎石底基層(200 mm)、碎石墊層(200 mm)，其結構合理，特別是面層采用先進的瀝青混合料結構。在厚度設計時，設計彎沉為22(1/100 mm)，即該市政道路的累計標準軸次為19 058 475次，按設計使用年限內交通量年平均增長率7%計算可知：使用初期雙向的日平均標準軸次為6 254.8次。計算得到土基模量為50 MPa。該路面在使用過程中需要校核路面結構的損傷。路面損傷一般包括疲勞開裂和永久變形兩方面。疲勞開裂的破壞極限可表示為：

Nf=f1(εf)-f2(Ef)-f3

(4)

式中：Nf——路面疲勞開裂前允許荷載重復次數；

εf——瀝青層底部的拉應變；

Ef——瀝青層的彈性模量；

f1，f2和f3——疲勞試驗得到的常數，本文中取值為f1=0.0636、f2=3.391和f3=0.854。

永久變形的破壞極限可表示為：

Nd=f4(εd)-f5

(5)

式中：Nd——路面產生永久變形前允許通過的荷載重復次數；

εd——土基表面的壓應變；

f4，f5——道路試驗得到，本文中取值為f4=1.365×10-9和f5=4.477。

對瀝青層底面拉應變和路基頂面壓應變進行的損傷分析。在分析過程中，假設瀝青層的材料為黏彈性材料，考慮路面的彈性模量隨四季變化，把一年分成四個季節進行分析。每個季節具有不同的彈性模量和蠕變柔量。防止疲勞開裂允許的荷載重復次數可以根據式(4)得到；防止永久變形允許的荷載重復次數可以根據式(5)得到。式(4)中的瀝青層(黏彈性材料)的彈性模量方程可表示為：

(6a)

或者

(6b)

式中:σ1，σ2和σ3——分別為三個主應力，滿足σ1>σ2>σ3；ε1為最小主應變，ε3為最大主應變。

不同時期每組荷載的損傷率可以通過預期的和允許的荷載重復次數之比得到，計算公式可表示為：

(7)

式中：Dr——年末的損傷率；

ni,j——i時期對應的預期重復次數j；

Ni,j——根據式(4)和(5)得到的允許荷載重復次數；

p——時期數；

m——荷載組數。

在瀝青路面的結構損傷分析過程中，需要分別計算疲勞開裂和永久變形兩種情況下的損傷設計壽命1/Dr，以壽命短的一項作為最終控制參數。

根據式(7)計算得知，該市政瀝青路面結構在一年內的拉應變損傷率為0.043 641，壓應變的損傷率為0.006 804 3，該路面面層結構為拉應變損傷控制，設計年限為23.11年。從損傷分析的結果可以得到，設計后路面結構的壽命比設計前增加了6年，并且設計后的壓應變比設計前降低了10倍，這表明設計后的瀝青路面有效地改善了路基的受力狀態。

4 結語

本文以太原市某瀝青路面工程為例，結合瀝青路面攤鋪過程出現的結構損傷問題，通過建立ARAC-13G、AC-20C和AC-25C瀝青混凝土的應力-疲勞方程，得出結論如下：

(1)對三種類型瀝青混凝土的疲勞試驗數據的線性回歸，得到了不同瀝青混凝土的疲勞方程。

(2)對該瀝青路面的結構損傷進行分析，得知設計后路面結構的壽命比設計前增加6年，且設計后的壓應變比設計前降低了10倍。