基于低維流形模型的圖拉普拉斯正則化的點云去噪算法

梁 宏

(江西理工大學 土木與測繪工程學院, 江西 贛州 341000)

三維激光掃描技術是獲取物體空間點云數據信息的重要手段之一,并在多個領域發揮著重要的作用[1-3]。但是受儀器測量誤差、物體反射、遮擋、光照以及環境變化等因素的影響,掃描獲取的初始點云數據模型中往往含有大量的噪聲點，這些噪聲點的數量越多，密度越大，對點云的影響也越大，因此需要采取合適的去噪算法將其去除。

近年來，國內外學者對點云去噪算法進行了較為深入的研究。Rosman等提出了一種通過斑塊協同頻譜分析對點云去噪的新方法[4]，該方法可以處理高水平的噪聲，同時保留清晰的表面特征；Mattei等提出了移動魯棒主成分分析算法[5]，該方法通過加權最小化保留銳利特征；Sun等提出了L0范數最小化的各向異性化點云去噪方法[6]，該方法可以在大量噪聲時恢復清晰的特征；Polat等提出一種LiDAR數據去噪算法[7]，該算法性能可以根據地區地形特征的變化而變化,可以有效濾除非地面點,是一種有效的點云去噪算法。Ma提出一種基于曲面擬合的去噪算法[8]，具有較好的去噪效果和較低的時間復雜度；Wang 等提出一種基于 Laplace 分布的去噪算法[9]，可以有效保留原始數據中有用細節信息；Cruz 等提出一種基于非局域增強卷積神經網絡的去噪算法[10]，通過結合卷積神經網絡和非局部濾波器實現了圖像的有效去噪；Centin 等提出一種幾何保真的 Signoroni 網格去噪算法[11]，對目標應用領域具有挑戰性的情況去噪效果良好；Zheng 等提出一種基于銳利特征骨架的點云去噪算法[12]，可以有效保持尖銳區域內的幾何特征；郭進等[13]提出了一種基于噪聲分類算法，可以去除小片噪聲；戴士杰等[14]提出了一種各向異性去噪算法，解決了去噪時模型失真問題；蘇本躍等[15]基于K-means聚類對點云進行去噪；馮東恒等[16]提出用共面法向量特征去除離群面的RANSAC 算法；許龍等[17]提出了基于模糊C均值和均值濾波的點云去噪算法；林洪彬等[18]提出基于參數自適應各向異性高斯核的散亂點云保特征去噪算法。

為了有效保留點云顯著的特征結構信息，進一步提高點云去噪的精度，本文提出了一種基于低維流形模型的圖拉普拉斯正則化的點云去噪算法， 通過采用低維流形模型，利用表面斑塊的自相似特性，同時對相似的斑塊進行去噪，以便更好地保留清晰特征；對流形的大小的計算是通過離散圖拉普拉斯正則化器來進行近似的，這大大降低了計算復雜度；針對離散的斑塊，設計了一種有效的相似性度量，用于噪聲的圖形構造。另外本文的圖拉普拉斯正則化器具有較好的穩定性。

1 基于低維流形的圖拉普拉斯正則化去噪算法

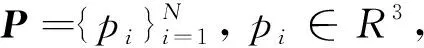
P=U+E

(1)

式中：U,E∈RN×3；U為點云的真實位置；E為噪聲(在本文實驗中假設為高斯噪聲)。為了消除噪聲，構建圖拉普拉斯低維流形來表示物體在空間域上的幾何結構，并提出基于流形的圖拉普拉斯正則化下的點云去噪模型。

1.1 低維流形表示

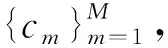
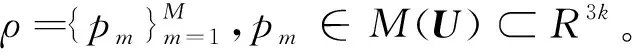
wmn=(ρmρn)-1/γφ(dmn)

(2)

式中，φ(dmn)為高斯核函數，即

(3)

式中，dmn為斑塊pm和pn之間的歐氏距離，即

(4)

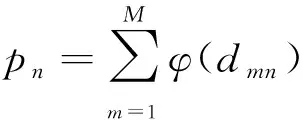
1.2 圖拉普拉斯正則化

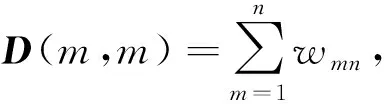
αi(p)=pi, ?p=[p1,…,p3k]T∈M

(5)

根據文獻[13]，流形λ在p點維度計算公式為

(6)

式中,?αi(p)表示函數αi在流行M上p點的梯度，所以得出

(7)

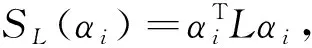
(8)

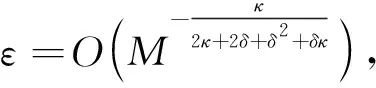
(9)

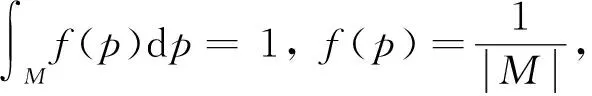
(10)

這樣得到了一個逐點收斂的正則化函數，相比較于對整個流形收斂來說，這樣更容易收斂。

(11)

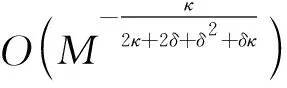
(12)

從式(12)可以看出拉普拉斯正則化可以不需要αi函數，因此繞過了對斑塊進行排序的問題。根據式(2)可知wmn也是距離dmn的函數，所以最后問題簡化成了求解斑塊之間的距離。

1.3 計算距離

為了計算第m和第n個斑塊的距離，在理想情況下可以把兩個斑塊內差到兩個連續的曲面上，那么斑塊的距離就是曲面函數局部區域上的積分。為了方便計算，定義一個參考平面，該平面與斑塊的中心相切并且與該點法線垂直。由于不同斑塊的法線方向不一樣，為了精確計算，在兩個斑塊上各自計算一次距離，它們的平均值即為所求。

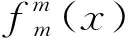
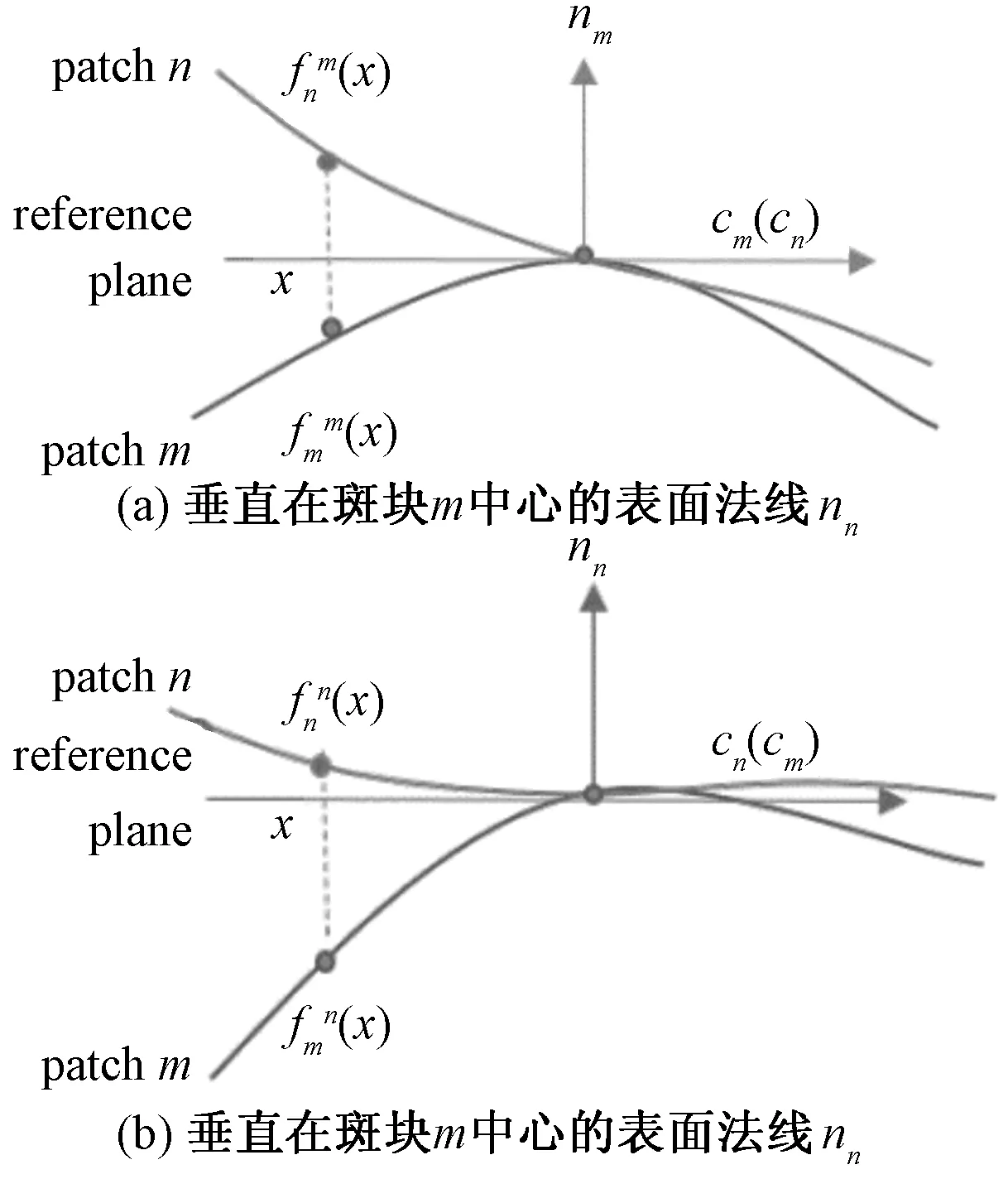
圖1 連續表面距離的測量

(13)

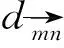
(14)

得到距離為

(15)

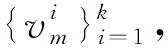
(16)

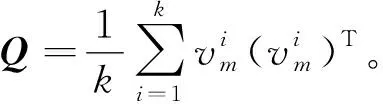
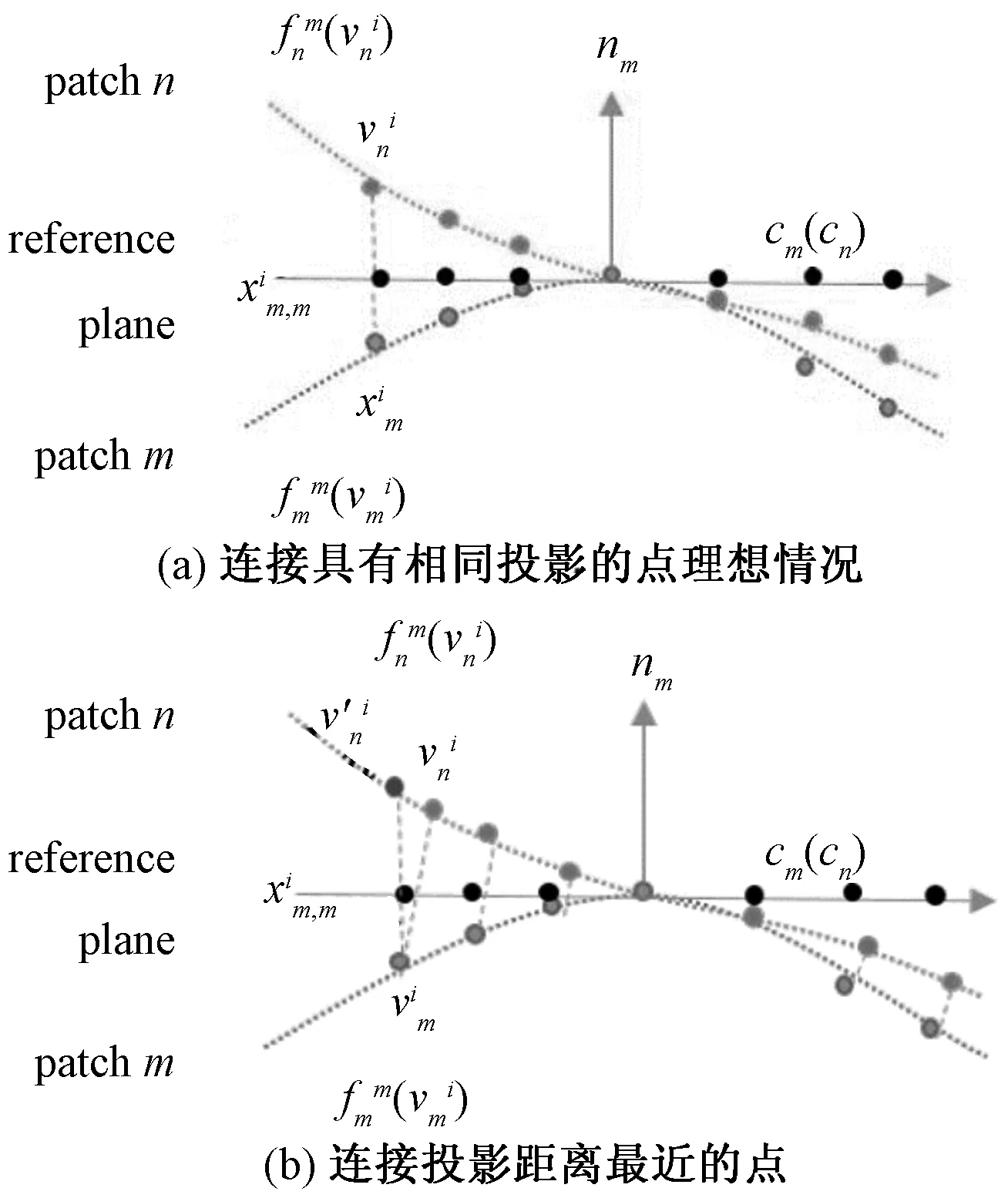
圖2 離散斑塊的距離測量

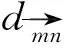
(17)

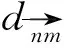
(18)

但有時，在該點附近找不到最近鄰點，這時為了找到與投影點對應的點，采用平面插值方法。對于點v，在另一個斑塊上找其對應的插值，找到3個投影距離最近的點形成一個平面，并找出點v沿法線方向在平面上的投影v′，此時計算距離就變得比較容易了。使用投影來找對應關系而不是通過點位置，是因為投影對噪聲具有良好的魯棒性。例如在圖3中，兩個斑塊的表面都是平面，通過投影計算的是垂直的直線距離，如果直接根據點位置計算距離就是水平的連線距離，這樣計算會導致去燥效果不佳。

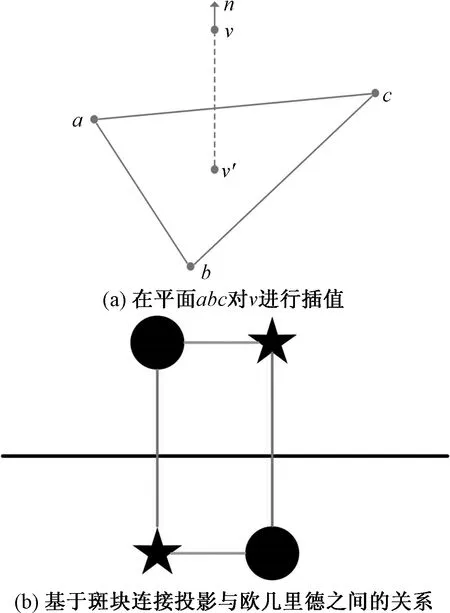
圖3 平面插值法

基于上面的斑塊測量方法，在不涉及插值時，第m和第n個斑塊連接取決于它們在參考平面上的投影，通過求出最小距離的方式找出了兩個斑塊的最近鄰點，但在邊上是加權無向的。

涉及插值后，v和a的權重wva定義為

(19)

式中：v為斑塊m上的點；點a、b、c為斑塊n上的點；dva為點v到a的距離；同理dvb、dvc也是v到點b、c的距離。

為了簡化實現過程，設置一個以k為最近鄰的窗口，計算出k最近鄰斑塊之間的距離，而不是直接計算點云中所有斑塊的距離。計算完成之后，構造出了一個點域圖，給出了圖拉普拉斯算子Lp∈RkM×kM，kM為所有斑塊的總點數。因此優化可以寫為

(20)

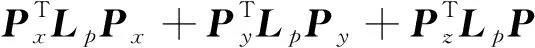
(21)

由于拉普拉斯算子依賴于斑塊坐標，采用交替優化的方法，在每次迭代中，修復Lp并求解U，然后在給定U的情況下更新Lp，然后重復進行直到收斂。在每一次迭代中，都可以根據之前的方法更新Lp，為了固定Lp優化U，每個點坐標(x,y,z)由下式給出：

(STLpS+μIq)Uq=μVq+STLpCq

(22)

式中：q∈{x,y,z}為坐標索引；Iq為與Lp大小相同的單位矩陣。迭代化求解，直到結果收斂。

2 實驗結果與分析

為了驗證本文點云去噪算法的有效性，對Anchor、Gargoyle、Lordquas、Dc、Daratech等模型進行測試。采用MATLAB程序編寫算法，在meshlab程序上的poisson重建算法對模型進行三維重建，驗證了本文算法有助于對邊緣特征的保留，不會導致過度平滑。為了加快實現速度，將50%的點當作斑塊中心，并使用最遠的點采樣來確保空間中的均勻采樣。將搜索窗口設置為16，將斑塊大小設置為30。在圖4中使用Anchor模型顯示迭代結果，標準偏差為0.01的高斯噪聲被添加到點云中。前3次迭代中的結果的表面重建如圖4(c)和(d)所示。迭代3次之后的結果收斂，因此只顯示前面3次迭代。參數μ=25exp(iteration)-1隨迭代增加。與其他方法的比較在圖5和圖6中，圖5中APSS的結果和RIMLS的結果在折疊區域和拐角處過度平滑。另外為了保證本文方法的準確性，對更多的模型進行了測試，將標準差為0.02、0.03、0.04的高斯噪聲添加到測試點云中，數值結果顯示在表1～表3中，其中本文算法具有最低的MSE。這些模型的參數μ=25exp(iteration/r)-1，其中對于σ=0.02、0.03、0.04的高斯噪聲，r=4、7、12。

圖4 Anchor模型在σ=0.01的去噪后表面重建結果

圖5 Anchor模型在σ=0.02的去噪后表面重建結果

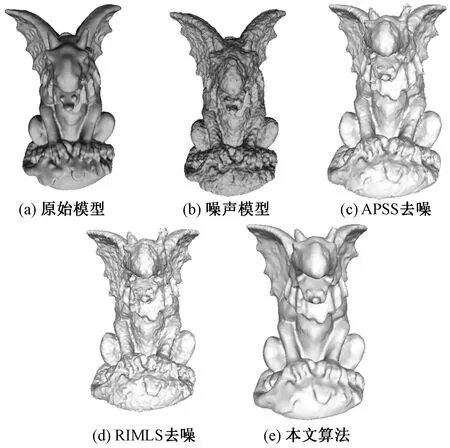
圖6 Gargoyle模型在σ=0.03的去噪后表面重建結果

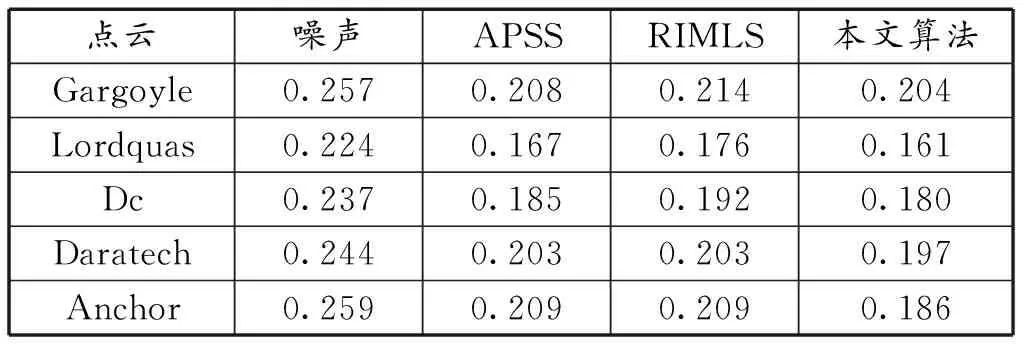
表1 具有高斯噪聲不同模型下的MSE(σ=0.02)

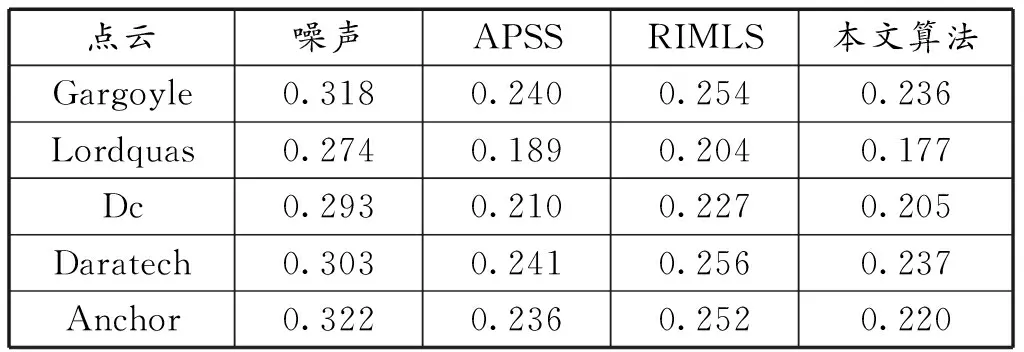
表2 具有高斯噪聲不同模型下的MSE(σ=0.03)

3 結論

提出了一種基于圖拉普拉斯正則化的3D點云去噪算法。得出以下結論：

1)提出的算法能普遍適用于有顯著幾何特征的噪聲點云，因為該方法針對的不是具體的形狀的點云，而是具有這個空間結構的所有的點云。

2)本文算法對比其他算法，在確保去噪精度的同時，能夠把物體的邊緣特征和顯著特征清晰地保留下來，同時不會在表面產生過度平滑。