基于常態挖掘路徑的液壓挖掘機軌跡規劃方法

馮明豪，任志貴,2，魏萬行，孫浩然，李佳豪

1陜西理工大學機械工程學院 陜西漢中 723000

2陜西省工業自動化重點實驗室 陜西漢中 723000

液壓挖掘機器人可以獨立工作，也可以遠程控制，已成未來挖掘機發展的重要方向之一[1]。軌跡規劃在挖掘機器人的控制中有非常重要的作用，直接影響挖掘機器人作業的運動平穩性和準確性[2]。挖掘機器人的操作過程就是通過軌跡規劃，將挖掘機的作業任務變成期望的運動和力，由底層控制環節生成相應的信號，產生相應的控制，使挖掘機器人輸出實際的運動和力，從而完成預期的作業任務[3]。一般來說，如果在沒有任何約束條件下，挖掘機器人的鏟斗齒尖作業起始點到終止點的軌跡有無數條，根據是否采用最優化方法進行最優軌跡尋找，可將軌跡規劃分為一般軌跡規劃和最優軌跡規劃[4]。李海虹等人[5]分別采用n次多項式法、傅里葉級數擬合法、分段多項式插值法對一條 T 型路徑進行一般軌跡規劃，對規劃前后的動力學特性進行對比評價，得出函數擬合法的軌跡規劃結果更平穩連續、振動強度更低的結論。潘雙夏等人[6]采用最優軌跡規劃方法優化了速度梯度和液壓缸的總移動距離，使得挖掘機的規劃軌跡更加穩定和節能，但軌跡規劃只應用在挖掘機修整平面作業的路徑上，其路徑實際上是一條直線。目前，對液壓挖掘機器人軌跡規劃的研究多數停留在簡單路徑，如直線、圓弧等[7]，未考慮應用在復雜路徑上，且挖掘工況主要集中在各液壓缸單獨挖掘的作業形式，復合挖掘的作業形式較少[8]。

筆者以減少液壓缸長度變化量作為優化目標，運用粒子群優化算法對一條真實復合挖掘路徑進行軌跡規劃，更符合挖掘機真實作業情況，同時達到減少挖掘機器人能耗的目的。

1 液壓挖掘機軌跡規劃流程

根據液壓挖掘機器人的結構，工作裝置可以簡要描述為位姿空間 [x，y，z，ξ]T、關節空間 [θ0，θ1，θ2，θ3]T和驅動空間 [θ0，λ1，λ2，λ3]T[9]。工作裝置連桿坐標系如圖 1 所示，ξ為姿態角，是水平方向與鏟斗齒尖和鏟斗鉸點連線之間的夾角[10]。

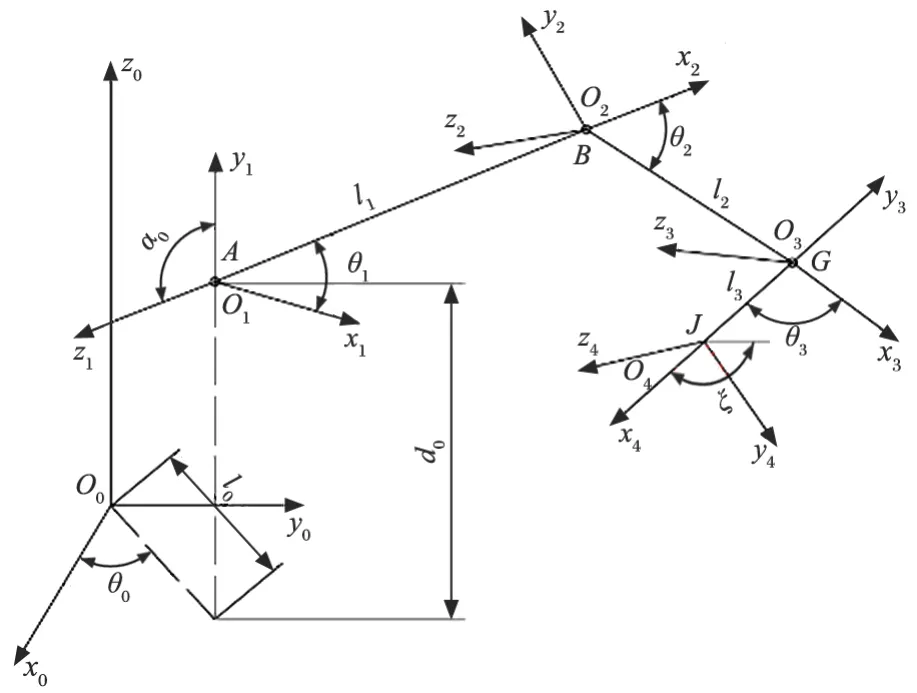
圖1 工作裝置連桿坐標系Fig.1 Coordinate system of linkage of working unit

基于機器人學，常用的液壓挖掘機軌跡規劃流程先規劃關節轉角，然后進行關節空間變量和位姿空間變量的相互轉換，使鏟斗齒尖達到預定的運動。而挖掘機在實際作業時，由于和工業機械手的作業對象不同，對姿態角的限制更為嚴格[11]。因此，筆者將以姿態角ξ作為控制變量，通過優化方法計算姿態角ξ，減少 2 個相鄰位姿之間的液壓缸長度變化量。

在確定預設路徑之后，對路徑上的點進行等步長分割離散化，確定每個離散點的 [x，y，z]T值。通過優化方法計算各離散點對應的姿態角ξ，確定位姿空間離散點坐標的 [x，y，z，ξ]T值后，由式 (1) 解出各離散點的關節空間坐標：

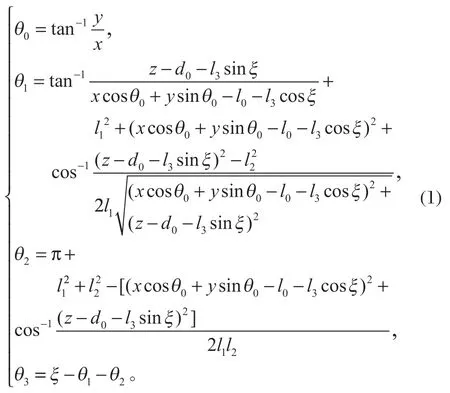
式中：θ1為zi-1軸從xi-1軸到xi軸的旋轉角度，規定逆時針方向為正；αi為xi軸從zi-1軸到zi軸的轉角，規定逆時針方向為正；li為連桿i的長度；di為xi-1軸與xi軸沿zi-1軸的垂直距離；i為連桿數量。

液壓挖掘機工作裝置機構簡圖如圖 2 所示。根據得到的各離散點關節空間坐標 [θ0，θ1，θ2，θ3]T值設定作業時間后，可以通過多項式插值方法完成軌跡規劃。基于各離散點的關節空間坐標值，還可以根據挖掘機的幾何結構，由式 (2)[12]計算出各離散點的驅動空間坐標 [θ0，λ1，λ2，λ3]T值：

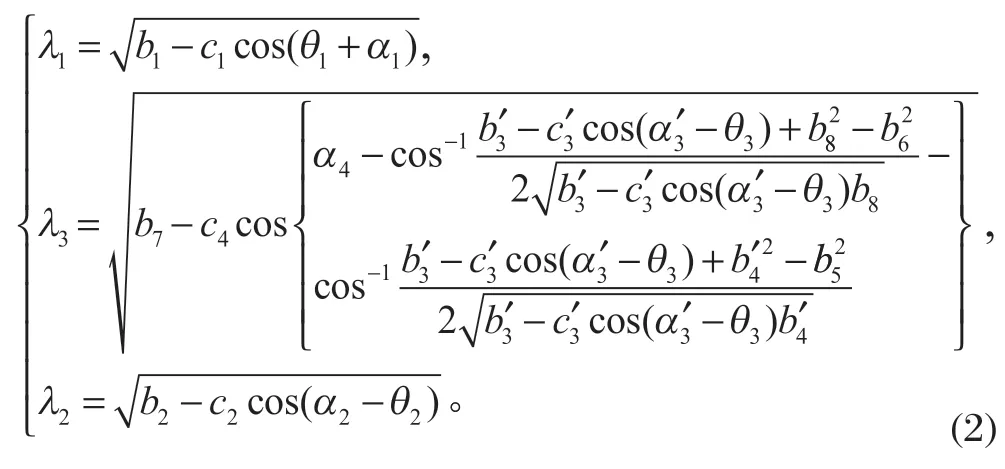
其中α1=∠BAC+∠FAx1，b1=AC2+AF2，c1=2AC·AF，如圖 2(a) 所示；

α2=π -∠GBH+∠ABD，b2=BD2+BH2，c2=2BD·BH，如圖 2(b) 所示；

α3′=π -∠JGL+∠BGN，b3′=GN2+GL2，α4=∠GNE，b4′=NG，b5=GL，如圖 2(c) 所示。

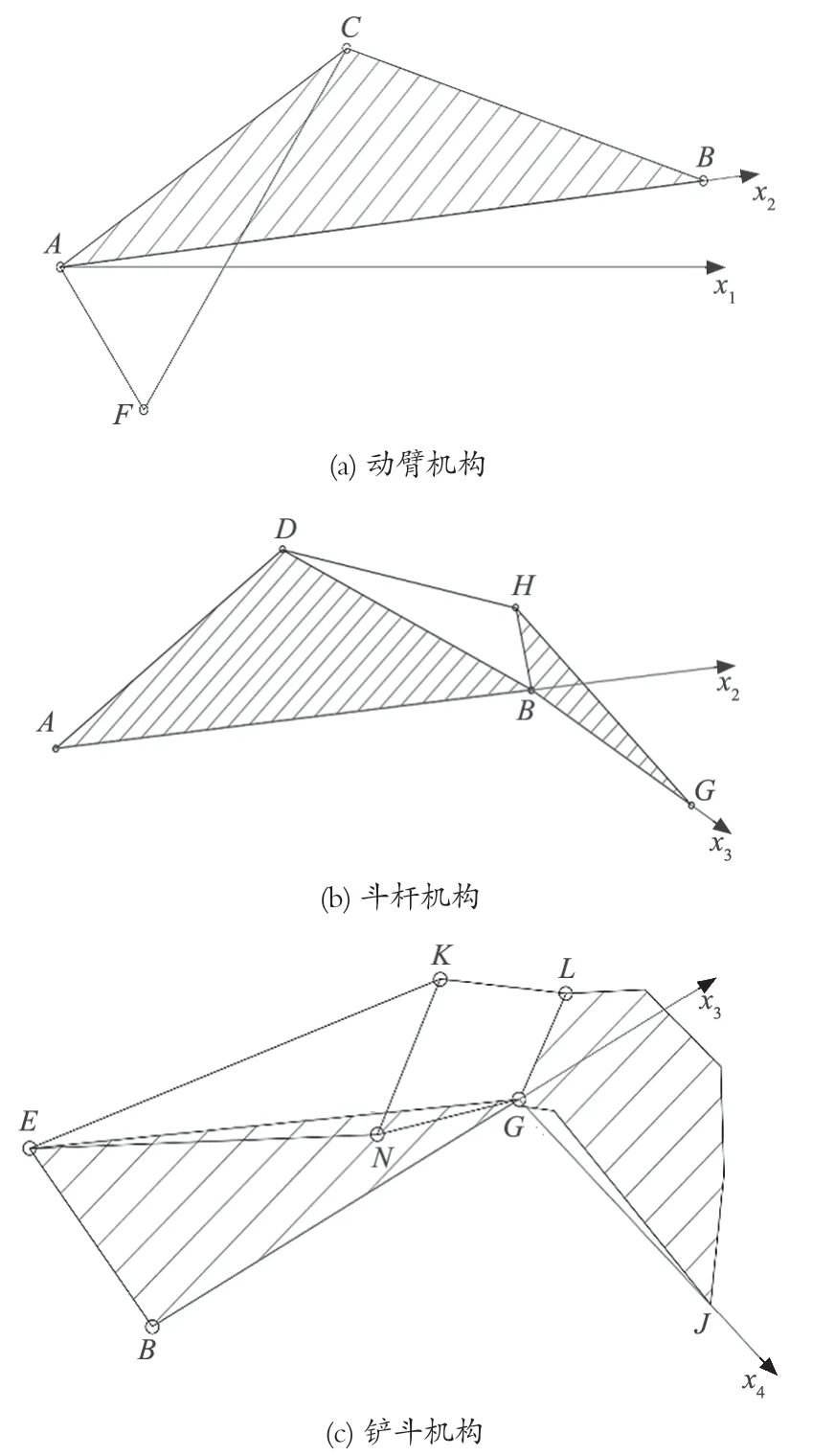
圖2 液壓挖掘機工作裝置機構簡圖Fig.2 Mechanism sketch of working unit of hydraulic excavator

2 軌跡規劃數學模型

2.1 目標函數

為了提高液壓挖掘機作業平穩性，降低能耗，將動臂機構、斗桿機構和鏟斗機構的相鄰位姿之間液壓缸長度變化量最小化作為優化目標。子目標函數如下：

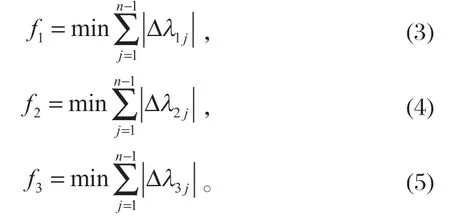
式中：n為軌跡曲線取點的數量。

根據挖掘機各工作裝置液壓缸長度變化范圍對挖掘機所有液壓缸長度之和的影響，經過無量綱處理后采用權系數法，對各子目標加上η1、η2和η3作為權重因子，滿足η1+η2+η3=1，將 3 個子目標函數集合為一個通用目標函數：

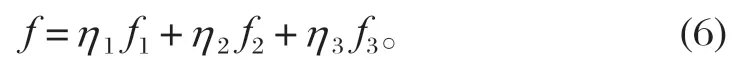
2.2 設計變量

將每一個離散點所對應的姿態角ξi(i=1～n) 作為優化的設計變量。

2.3 約束條件

(1) 關節轉角約束 動臂、斗桿、鏟斗關節轉角不應超過各部分轉角限制。

(2) 液壓缸長度約束 動臂、斗桿、鏟斗液壓缸長度不應超過各部分液壓缸長度限制。

(3) 姿態角約束 在挖掘機工作范圍內，當鏟斗齒尖的空間位置確定時，其姿態角不可能為 360°范圍內的任意角，那么鏟斗齒尖所在的位置相對于其不能實現的姿態角范圍是盲位，這一不能實現的姿態成為該位置的盲角。由于盲位與盲角的存在，導致挖掘機鏟斗位于某個位置時，往往不能實現特定的姿態；反之，當鏟斗處于某種姿態時不能到達所要求的位置，這意味著挖掘機在作業過程中，可能不能同時完成任意位置和姿態的要求。在某一點位姿空間坐標 [x，y，z]T值給定的情況下，姿態角允許的范圍為 (ξ0，ξf)，任意點姿態角范圍的計算[13]如下：當θ1=θ1max，或θ2=θ2min、θ3=θ3max時，會出現ξ0；當θ1=θ1min、θ2=θ2max，或θ3=θ3min時，會出現ξf。

3 不同規劃方法的對比分析

由于在真實復合挖掘路徑上驗證各方法的節能效果比較困難，而 T 型路徑由D1～D6這 6 個點連成的直線組成，計算相對簡單，遂選用 T 型路徑進行驗證。以某 8.5 t 挖掘機在一條 T 型路徑 (見圖 3) 上作業為例，對 3 種規劃方法進行對比分析，再選擇節能效果最好的方法對真實復合挖掘路徑進行軌跡規劃。

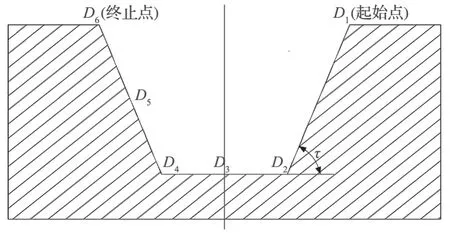
圖3 T 型路徑Fig.3 T-shaped path

3.1 經驗法

在挖掘機軌跡規劃的經驗法中[14]，將切削后角β設為定值，當后角出現盲角時，調整后角消盲。通過下式計算出每一點的姿態角：

式中：τ為路徑上某一點與x軸正方向的夾角，如圖4 所示。

再依據已知的 T 型路徑上各點的 [x，y，z]T值，根據第 1 節中的軌跡規劃流程得出液壓缸長度變化的計算結果，如圖 4 所示。

圖4 采用經驗法得到的液壓缸長度變化曲線Fig.4 Variation curves of length of hydraulic cylinders obtained with empirical method

3.2 MATLAB 優化工具箱

將第 2 節所提到的目標函數、設計變量和約束條件輸入 MATLAB 優化工具箱，采用其中的 fmincon函數，以經驗法的各離散點的姿態角值作為初始值，得出優化后各離散點的姿態角值，并根據第 1 節中的軌跡規劃流程得出液壓缸長度變化的計算結果，如圖5 中的 3 條實線曲線 (O 組曲線) 所示。相比于圖 4 中經驗法的規劃效果，采用 MATLAB 優化工具箱后的液壓缸變向點明顯減少，即由于液壓缸閥門頻繁換向所產生的振動有所減小。

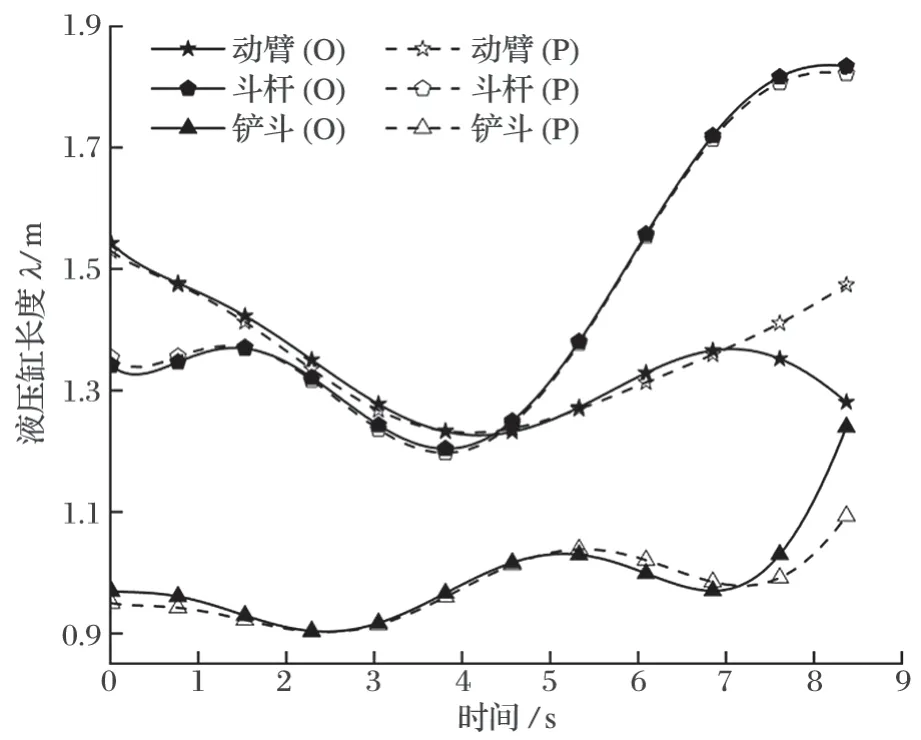
圖5 采用 MATLAB 優化工具箱和粒子群優化算法得出的液壓缸長度變化對比Fig.5 Comparison of length variation of hydraulic cylinders obtained with MATLAB optimization toolbox and PSO algorithm

3.3 粒子群優化算法

采用粒子群優化算法進行軌跡規劃，設置粒子群數量為 1 500 個，粒子維數為每段直線離散點數量，最大迭代數為 200，慣性權重為 0.5，學習因子c1、c2均為 2，得到優化后的各離散點的姿態角值，同樣根據第 1 節中的軌跡規劃流程得出液壓缸長度變化的計算結果，如圖 5 中 3 條虛線曲線 (P 組曲線) 所示。相比于圖 4 中經驗法的規劃效果，采用粒子群優化算法得到的液壓缸變向點數量明顯減少，且相較于采用MATLAB 優化工具箱的變向點數量更少，因而粒子群優化算法比 MATLAB 優化工具箱法的規劃效果更好。在接近時間末端時，采用粒子群優化算法得到的液壓缸長度變化曲線更平滑，突變更小。采用 2 種優化方法相對于經驗法的改進效率如表 1 所列 (其中x為第2.1 節中目標函數的計算結果，即液壓缸最小長度變化量，表 3 同)。從表 1 可以看出，采用粒子群優化算法得到的總液壓缸長度變化量更少，能耗更低，優化效果更好。

表1 采用 MATLAB 優化工具箱和粒子群優化算法相對于經驗法的改進效果對比Tab.1 Improvement effects of MATLBA optimization toolbox and PSO algorithm compared with expirical method

4 基于常態挖掘路徑的軌跡規劃

4.1 常態挖掘路徑選取

測試機型為某 36 t 的反鏟液壓挖掘機，基本參數如表 2 所列。測試地點為湖州某試驗場，挖掘對象為混有石塊的Ⅲ級土壤，作業現場如圖 6 所示。采用傾角傳感器對挖掘機各關節角位移進行測量[15]，取停機面最大半徑挖掘工況作為本次軌跡規劃路徑。由于受到客觀條件的限制，直接對此路徑進行連續軌跡規劃比較困難，取路徑擬合結果所得路徑方程進行軌跡規劃，結果如圖 7 所示。

圖6 作業現場Fig.6 Operation scene

表2 測試機型基本參數Tab.2 Basic parameters of test excavator

4.2 停機面最大半徑挖掘路徑軌跡規劃

選擇粒子群優化算法按照第 1 節中的軌跡規劃流程進行軌跡規劃，結果如圖 8 中 A 組 3 條虛線曲線所示。將其與試驗得到的液壓缸長度變化曲線 (B 組 3條實線曲線) 進行對比可知，兩者除動臂液壓缸長度變化接近外，采用粒子群優化算法得到的液壓缸變向點數量減少，液壓缸長度變化時過渡更加平滑。采用粒子群優化算法相對于試驗結果的改進效果如表 3 所列。

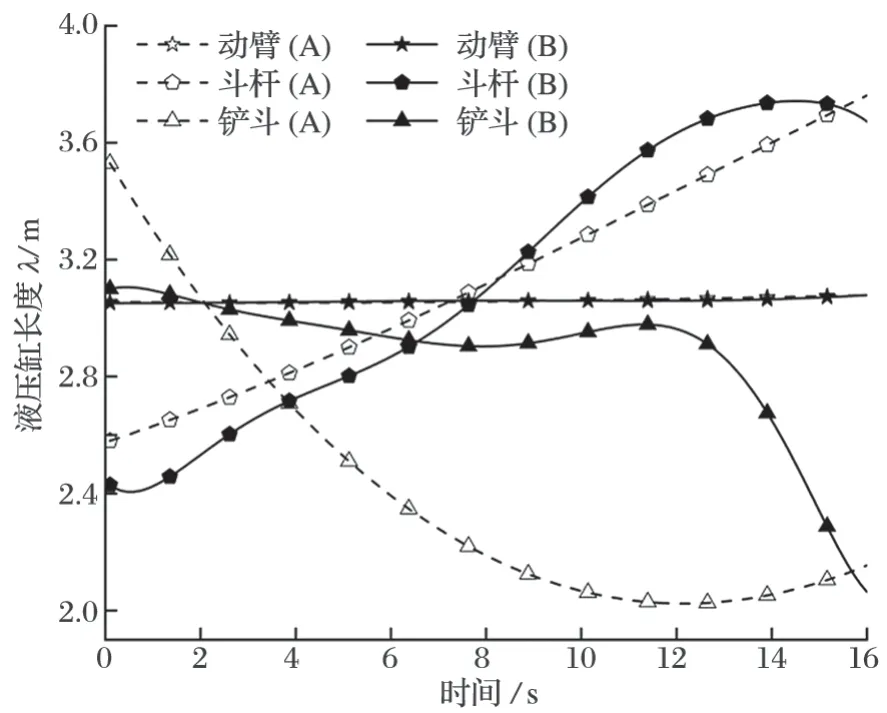
圖8 采用粒子群優化算法與試驗得到的液壓缸長度變化對比Fig.8 Comparison of length variation of hydraulic cylinders obtained with PSO algorithm and test

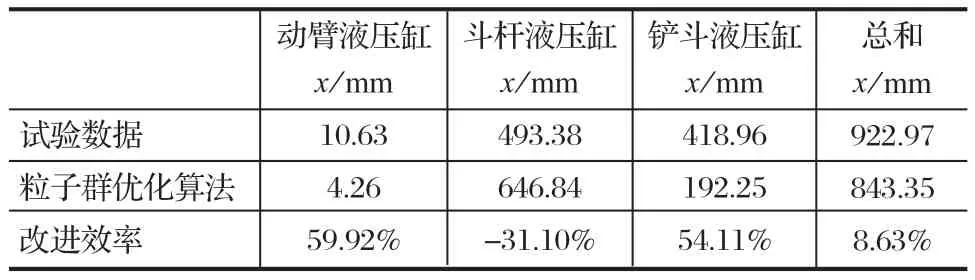
表3 采用粒子群優化算法相對于試驗結果的改進效果Tab.3 Improvement effects of PSO algorithm compared with test data

由于對各關節在中間點時的速度有約束，所以采用 4-3-3-……-3-3-4 多項式插值方法[16]得到的軌跡規劃結果如圖 9～ 11 所示。由圖 9～ 11 可知：各關節角位移、角速度變化曲線平滑連續，角加速度變化曲線連續，保證了各關節角變化平穩連續；起始點、終止點速度、加速度均為零，能夠完成連續路徑下的全過程工作，滿足挖掘機挖掘過程中的性能要求。

圖9 角位移變化曲線Fig.9 Variation curves of angular displacement

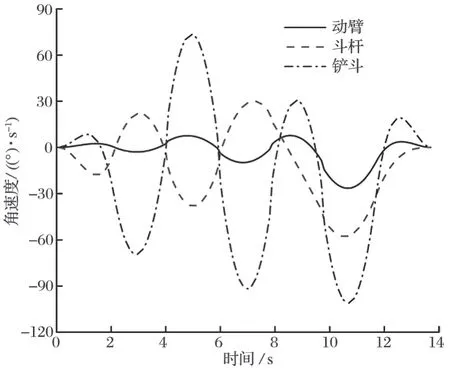
圖10 角速度變化曲線Fig.10 Variation curves of angular velocity

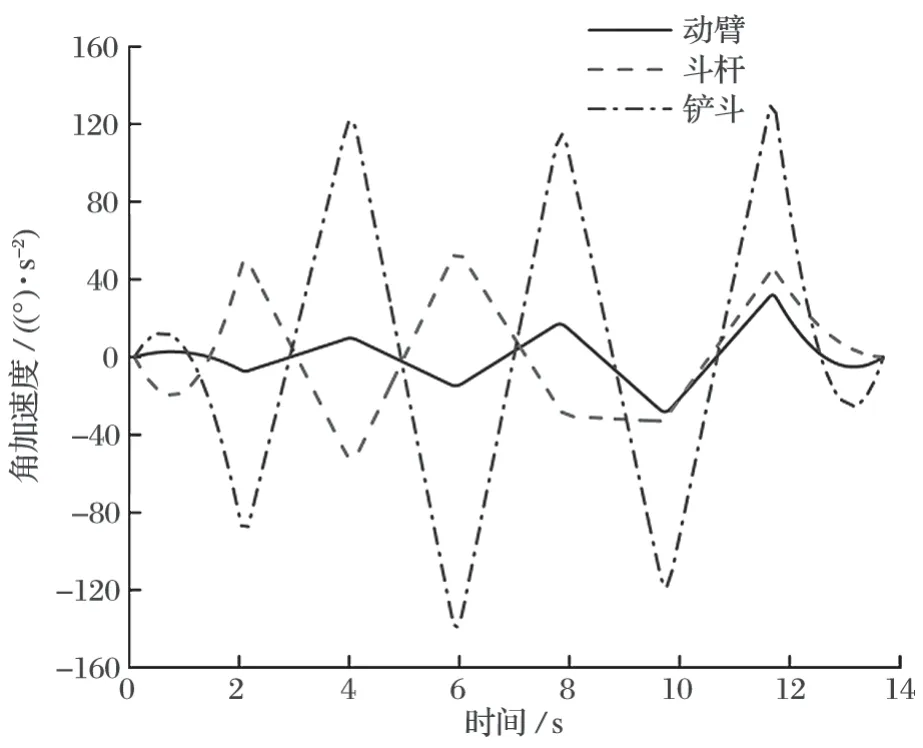
圖11 角加速度變化曲線Fig.11 Variation curves of angular acceleration

5 結語

在分析液壓挖掘機工作機理及運動學建模基礎上，通過對 3 種方法的比較，以挖掘機器人工作平穩性和節能作為重點，選擇采用粒子群優化算法對挖掘機器人運動軌跡進行規劃，在一條實際復合挖掘路徑上加以驗證，并與試驗數據進行對比，得出該方法效果良好的結論。對于復合挖掘來說，筆者對挖掘機器人動力學部分涉及不夠，針對這點，會在后續研究中進一步深入。