區域與空間視角下中國城市規模分布與增長

摘 要：檢驗齊普夫定律和吉布拉定律在中國城市規模分布和增長中的適用性，有利于分析中國城市體系的演變趨勢和合理化特征。研究表明：中國城市規模分布基本服從齊普夫定律，但存在明顯的分化特征和趨勢;中部地區城市規模分布呈現扁平化特征，而其他區域均存在明顯的分化特征和趨勢，這與其內部城市規模的差異相關;全國和區域層面城市規模增長基本服從吉布拉定律，這與小城市和大城市人口增長較快，而中等城市人口增長較慢相關。因此國家需要調整未來城鎮化發展的重點，在中部地區應當注重發展大城市，而其他地區應當注重大中小城市協調發展;另外還需要加大對中等城市的政策傾斜和增強大城市的空間溢出效應，以促進中等城市人口增長。

關鍵詞：人口城鎮化;城市規模;齊普夫定律;吉布拉定律

中圖分類號：F291.1

文獻標識碼：A

文章編號：1000-4149（2021）05-0081-14

DOI：10.3969/j.issn.1000-4149.2021.00.041

收稿日期：2021-02-01

;修訂日期：2021-06-08

基金項目：國家社會科學基金項目“戶籍管制下城市差異化公共服務供給與人口空間集聚優化研究”（18BRK017）;國家社會科學基金項目“城市群戰略下中心城市人口集聚的時空演變與空間效應研究”（20BRK019）;中南財經政法大學中央高校基本科研業務費項目“中國城市人口集聚的區域差異與分布動態演進”（2722020JCG011）。

作者簡介：楊曉軍，經濟學博士，中南財經政法大學經濟學院副教授。

The Distribution and Growth of Chinas City Size from Regional

and Spatial Perspective

YANG? Xiaojun

（School of Economics， Zhongnan University of Economics and Law，

Wuhan 430073， China）

Abstract：Testing the applicability of Zipfs law and Gibrats law in the distribution and growth of Chinas city size is helpful to analyze the evolution trend and rationalization characteristics of Chinas urban system. The results show that Chinas city size distribution generally obeys Zipfs law， but there are obvious divergence features and trends. The distribution of city size presents a flat feature in the central region， while other regions have obvious divergence features and trends， which are related to their inter-region difference. The growth of city size at the national and regional levels basically obeys Gibrats law， which is related to the rapid population growth of small and big cities， while the slower growth of population in medium-sized cities. Therefore， the focus of future urbanization development needs to be adjusted， and the central region should focus on the development of big cities， while other regions should focus on the coordinated development of big， medium and small cities. It is also necessary to increase policy inclination for medium-sized cities and enhance the spatial spillover effect of big cities to ensure population growth in medium-sized cities.

Keywords：urbanization; city size;Zipfs law;Gibrats law

一、引言

中國城鎮化的路徑選擇存在以大城市為主的集中式和以小城鎮為主的分散式兩種觀點，其爭論焦點在于城市體系合理化。一個國家城市體系的合理化有利于高效優化要素資源分配和充分發揮集聚（或擴散）效益優勢，這就需要不同規模的城市相互依存、共同發展，既要充分發揮大城市的集聚與輻射效應，又要注重增強中小城市和小城鎮的容納與吸收作用，從而實現大中小城市和小城鎮的協調發展。關于合理城市體系的研究既有

基于人口或經濟規模等單一指標的分析，也有基于經濟、社會、生態等綜合指標的分析，本文的討論主要是基于城市人口規模指標。現有文獻主要通過齊普夫（Zipf）定律和吉布拉（Gibrat）定律來檢驗城市體系是否合理化。因此，利用最新數據來檢驗齊普夫定律和吉布拉定律在中國城市規模分布和增長中的應用，以揭示城市規模的空間分布動態特征，有助于更好地促進城市規模分布格局的優化與調整，對推動新型城鎮化進程和實現城市體系合理化具有重要的現實意義和理論價值。

齊普夫研究表明城市規模分布不僅服從帕累托分布，而且帕累托指數為1[1]，這就是所謂的“齊普夫定律”或“位序—規模法則”，它通常作為一種檢驗城市體系合理的標準，以此來判斷城市規模分布是否合理化。

吉布拉認為城市規模的增長率與其初始規模無關，即不同規模城市的人口增長率沒有顯著差別，都保持在自然增長率水平，這被學者們稱之為“吉布拉定律”[2]。

隨后國外學者們運用不同國家或地區的實證數據來驗證其有效性，研究結果存在差異：一是認為城市規模分布遵循齊普夫定律[3-5];二是認為城市規模服從帕累托分布，但帕累托指數大于或小于1[6-9];三是認為城市規模上尾部分的分布遵循齊普夫定律[10-11];四是認為城市規模分布服從對數正態分布，且城市規模與其增長率無關，滿足吉布拉定律[12-15];五是認為城市規模分布服從雙帕累托對數正態分布[16]。中國正處于城鎮化快速發展階段，其城市規模分布和增長也隨之不斷變化和調整，國內外學者運用上述方法對中國城市人口規模分布和增長進行了驗證。有的學者認為其服從帕累托分布，存在明顯的區域特征[17]，且基本服從齊普夫定律[18]，人口在不同規模城市間的分布逐漸趨于合理[19];但也有學者認為其并不服從齊普夫定律[20-21]，而是呈現出典型的扁平化特征，表現為大城市和小城市、小城鎮相對較少，中等城市分布密度較高，特大型城市相對合理[22]，這也與小城市高速增長及中等規模城市增長相對停滯密切相關[23];還有學者認為其符合雙帕累托對數正態分布，且擁有對數正態分布的中間主體，上下尾部更接近冪律分布，這與處于上尾的大中城市數量和人口規模增長迅速，處于下尾的中小城市數量多但人口規模增長動力相對不足有關[24]，且總體上不滿足吉布拉定律，這與城鎮化發展階段密切相關[25]。

上述研究為本文提供了很好的經驗借鑒，但也存在進一步探討的問題，如現有文獻所使用的數據多為不同時點的截面數據，且衡量城市規模指標存在爭議;時間范圍上主要在2010年以前，需要更新數據分析其最新特征;研究范圍主要是全國總體為主，較少涉及區域層面;未考慮城市規模分布與增長的空間依賴性。因此，本文根據2006—2017年中國縣級及以上城市面板數據，構建衡量城市規模的指標，基于全國、區域和空間視角檢驗齊普夫定律和吉布拉定律在中國城市規模分布和增長中的適用性，分析中國城市體系的演變特征和合理化趨勢，并據此提出相應的政策建議。

二、數據與典型化事實

1. 數據

現有研究中衡量城市規模的指標主要有兩類：一是來自美國國防氣象衛星計劃/線性掃描系統（DMSP/OLS）的夜間燈光數據[23，26-29]，它是一個較好的替代衡量指標，但不能精確衡量城市人口數;二是基于人口統計數據指標，包括《中國城市統計年鑒》中的市轄區戶籍人口指標[17，30]、《中國城市建設統計年鑒》中的城區常住人口指標[19]、全國人口普查數據中的城鎮常住人口指標[22，25，31-32]和聯合國人口司編撰的《世界城市化展望》中的市域城鎮人口指標[24，33]。上述指標涉及城鎮、市轄區和城區三個范圍，具體來看，城鎮包括設市建制的城市市區和建制鎮的鎮區，市轄區包括城區和郊區人口，而城區主要是城市市政設施建設和經濟發展的核心區，因而相對于城鎮和市轄區而言，城區能夠更準確地反映城市的范圍。此外，2014年國務院印發的《關于調整城市規模劃分標準的通知》中也將城區常住人口作為衡量城市規模的依據。基于此，本文采用城區常住人口指標衡量城市規模。

由于《中國城市建設統計年鑒》中準確衡量城區常住人口數據起始于2006年，因此本文將時間范圍限定在2006—2017年。在樣本數據期，由于撤縣設區和新設縣級市等行政區劃調整引起城市數量發生變化，為保持每個年度城市數量一致以便于比較分析，本文將考察期內27個撤縣設區的縣級市在撤銷前的人口數據并入相應的地級市，并刪除32個新設縣級市，最終數據處理后共獲得628個城市數據。關于城市規模的劃分標準，根據2014年11月國務院印發的《關于調整城市規模劃分標準的通知》（國發〔2014〕51號），以城區常住人口為統計口徑，其中城區常住人口50萬以下的城市為小城市，城區常住人口50萬以上100萬以下的城市為中等城市，城區常住人口100萬以上500萬以下的城市為大城市，城區常住人口500萬以上1000萬以下的城市為特大城市，城區常住人口1000萬以上的城市為超大城市。

2. 典型化事實

中國城市規模具有明顯的空間非均衡性態勢，這已經成為城鎮化進程中的客觀存在。因此需要考察區域層面城市規模的差異性。關于區域劃分標準，本文依據國家統計局2011年6月公布的《東西中部和東北地區劃分方法》，將我國的經濟區域劃分為東部、中部、西部和東北部四大地區，其中東部地區包括北京、天津、河北、上海、江蘇、浙江、福建、山東、廣東和海南10個省和直轄市;中部地區包括山西、安徽、江西、河南、湖北和湖南6個省;西部地區包括內蒙古、廣西、重慶、四川、貴州、云南、西藏、陜西、甘肅、寧夏、青海和新疆12個省、自治區和直轄市;東北地區包括遼寧、吉林、黑龍江3個省。最終樣本中，東部、中部、西部和東北地區分別選擇210、167、165和86個城市。

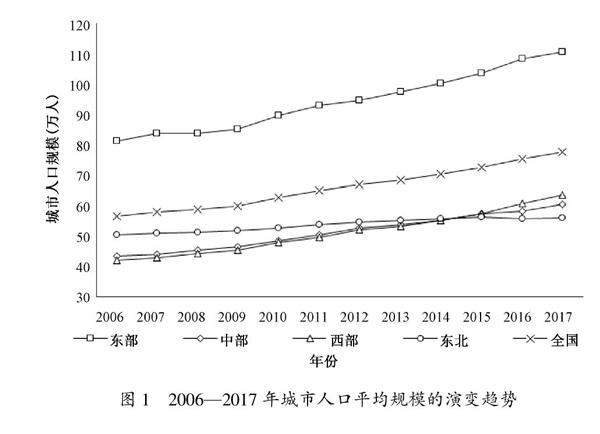
為了揭示考察期內城市規模的演變趨勢，本文對全國及各區域城市人口規模進行均值處理，具體如圖1所示。從演變趨勢來看，考察期內全國及各區域城市人口平均規模均呈現出明顯的上升趨勢。在增長數量方面，東部城市人口平均規模的增長數量最高，年均增長量為2.69萬人;其次是西部城市，年均增長量為1.95萬人;再次是中部城市，年均增長量為1.57萬人;最后是東北部城市，年均增長量僅為0.51萬人。在增長速度方面，西部城市人口平均規模的增長速度最快，年均增長率為3.81%;其次是中部城市，年均增長率為3.08%;再次是東部城市，年均增長率為2.86%;最后是東北部城市，年均增長率僅為0.96%。在差異程度方面，考察期內區域間城市人口平均規模的絕對差異明顯，極差呈現出不斷擴大的趨勢，從2006年的39.24萬人擴大到2017年的54.83萬人。具體來看，東部城市人口平均規模一直處于最高水平，平均值為94.51萬人，遠高于全國城市平均水平;其他三個區域的城市平均人口規模均低于全國平均水平，且差異不明顯。

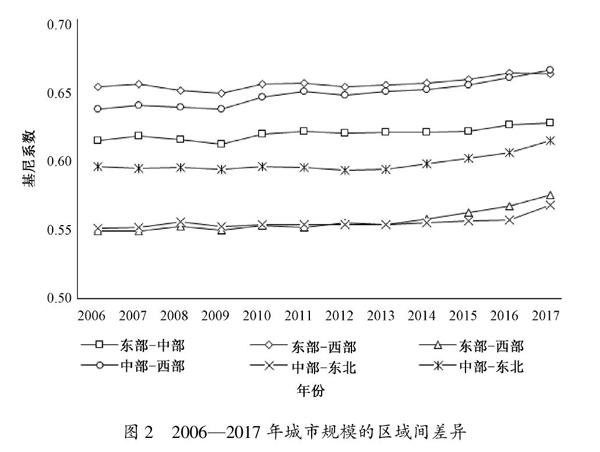
為了詳細反映中國城市規模的區域間差異，本文利用達古姆（Dagum）基尼系數[34]進行測算，結果如圖2所示。總體來看，四大區域間城市規模存在較大差異且呈現擴大化趨勢。從數值來看，東部與西部、中部與西部的區域間城市人口規模差異最大，其基尼系數的均值分別為0.67和0.65;東部與中部、西部與東北的區域間差異較大，其基尼系數的均值分別為0.62和0.60;東部和東北、中部和東北的區域間差異較小，其基尼系數的均值分別為0.56和0.56。從演變趨勢來看，各區域間城市人口規模差異總體上呈現小幅上升趨勢，但其增長速度存在差異，如東部與東北區域間差異的增長速度最快，其基尼系數的年均增長率為0.42%，而東部與西部區域間差異的增長速度最慢，其基尼系數的年均增長率僅為0.13%。由此可見，中國城市規模存在較高的區域間差異，因此區域層面分析有助于更好地了解其特征。

三、城市規模分布：齊普夫定律檢驗

1. 經驗估計

大量文獻采用帕累托指數研究城市規模分布狀況，具體公式為：

R=A·P-a（1）

其中，R為城市位序，即一個城市的規模在全國或區域內的排列次序，P為城市規模，a為描述城市規模分布形狀的參數（即帕累托指數），且a>0，A為參數。現有實證研究通常估計帕累托指數是否為1以及其隨時間變化的趨勢。如果a等于1，說明城市規模分布滿足齊普夫定律，即中國城市體系比較合理;而a不等于1則意味著城市規模分布不滿足齊普夫定律。如果a值越大，說明城市規模越均勻，反之城市規模越集中;a值逐漸增加，說明城市規模分布呈現扁平化趨勢，反之城市規模分布呈現分化趨勢。

本文利用極大似然估計對樣本數據是否符合帕累托分布進行檢驗，由于篇幅受限，其結果備索。結果表明不同樣本城市規模分布均在1%的顯著性水平上通過了帕累托檢驗，說明中國城市規模分布服從帕累托分布。因此建立實證模型來估計帕累托指數：

lnR=c-alnP+ε（2）

其中，c為常數，ε為誤差項。

加貝克斯（Gabaix）和伊布拉吉莫夫（Ibragimov）研究表明，式（2）的OLS回歸結果可能存在偏差，需要對模型中的城市位序進行修正[35]，具體模型如下：

ln（R-1/2）=c-alnP+ε（3）

表1報告了中國城市規模分布的Gabaix-Ibragimov回歸結果。結果表明，總體樣本中，帕累托指數位于0.951—0.991之間且通過1%的顯著性水平，說明中國城市規模總體分布近似滿足齊普夫定律，中國的城市體系比較合理。隨著城市樣本選取量的增加，帕累托指數逐漸減少，即隨著中小城市數量增加，中國城市規模分布呈現分化趨勢，人口向大城市集聚的現象尤為突出;隨著時間推移，各城市樣本的帕累托指數也呈現出減少趨勢，尤其是2011年以后各城市樣本的下降趨勢非常明顯

，說明中國城市體系從2011年開始出現不合理的態勢，這與城市化進程中重點發展大城市，忽視中小城市發展密切相關。此外，我們注意到截點城市的選擇與齊普夫定律是否成立存在極大關系，因此通過編撰計算程序測算出帕累托指數最接近1時所對應的城市數量，即最優截點城市數量。結果顯示，最優截點城市數量其范圍在611—626之間，非常接近本文選取的城市樣本量，這也進一步說明齊普夫定律在中國城市規模分布中有較好的適用性和合理性。

下面進一步檢驗區域層面城市規模分布是否與全國樣本存在顯著差異。表2報告了區域層面城市規模分布的Gabaix-Ibragimov回歸結果。結果表明，各區域城市規模總體分布也近似滿足齊普夫定律，但也存在差異性。其中，中部地區的帕累托指數大于1而其他地區均小于1，說明中部地區城市規模分布存在扁平化特征，而其他地區存在分化特征。隨著時間推移，各區域城市樣本的帕累托指數均呈現下降趨勢，即城市規模分布的分化趨勢逐漸明顯。綜合來看，中部地區城市規模分布比較均勻，而其他地區存在明顯的集聚現象。

2. 空間距離約束

由于人口在城市間可以自由流動，一個城市與鄰近城市的人口之間存在密切聯系，即城市規模分布存在空間依賴性 [36]。因此，本文通過基于距離的城市地理樣本選擇，引入空間變量分析城市規模分布隨地理距離變化的規律。第一步是確定鄰近城市的地理樣本，根據空間地理距離考慮半徑500公里范圍內城市的所有可能性組合，其中城市間地理距離數據來源于國家基礎地理信息系統1∶400萬中國地形數據庫，并利用ArcGIS軟件進行測算。以一個城市為中心，從城市間最短距離10公里開始，選擇每增加10公里的城市樣本，最終形成了49個距離樣本和20904個城市樣本數據。

在這些樣本數據中，所有規模的城市均被考慮在內。由于在不同城市的相同距離樣本中會包括完全相同的城市，在此刪除重復值。第二步是利用極大似然估計對每個距離樣本數據進行帕累托分布檢驗，結果表明2006—2017年49個距離樣本數據均服從帕累托分布。第三步是采用Gabaix-Ibragimov回歸模型估計每個距離樣本城市規模分布的帕累托指數，最終每年可以獲得49個不同的估計值。第四步是使用局部多項式平滑對地理距離和估計的帕累托指數之間的關系進行非參數估計。本文僅列示了部分年份的非參數估計結果，如圖3所示，圖中虛線部分為95%的置信區間。結果表明，隨著地理距離增加，帕累托指數總體呈現下降趨勢，且在100公里范圍內的下降趨勢非常明顯，在100—500公里范圍內，帕累托指數呈現出波動趨勢，且近似等于1。從時間趨勢來看，在不同地理距離上，2006年帕累托指數主要大于1，而2017年卻小于1，這說明隨著時間推移，城市規模分布的分化趨勢逐漸明顯，這與上述分析相一致。綜合來看，考慮到空間因素后，中國城市規模分布也近似滿足齊普夫定律，且分化趨勢日趨明顯。

四、城市規模增長：吉布拉定律檢驗

1. 線性模型估計

吉布拉定律主要用來考察城市規模增長率與初始規模的關系，本文建立如下回歸模型：

gi=α+βlnPi+εi（4）

其中，g為城市規模的標準化增長率，即增長率減均值再除以標準差;α為常數，β為回歸系數;i為某個城市，ε為誤差項。如果β為零或者不顯著，則表明城市增長率與其初始規模無關，即城市規模增長滿足吉布拉定律，反之則表明吉布拉定律假設不成立，即城市規模體系沒有達到最優狀態。

考慮到城市規模增長率與間隔時間密切相關，本文對其取值范圍限定在1—11年，以盡可能了解城市規模增長率的準確變化趨勢，進而增強模型檢驗的有效性。表3報告了中國城市初始規模對不同時間間隔增長率的回歸結果。從結果可以看出，城市初始規模對增長率的影響存在較大差異。具體來看，2006年城市規模與其2—8年增長率，2007年城市規模與其1—7年增長率，2008年城市規模與其1—5年增長率均呈現顯著的負相關，這說明初始規模較大的城市往往具有較低的增長率，即表明吉布拉定律假設不成立。2009年和2010年城市規模對不同增長率的影響均不顯著，則表明吉布拉定律假設成立。從2011年開始，城市規模對增長率的影響開始呈現顯著正相關，說明吉布拉定律假設不成立。綜上所述，從年份來看，2009—2010年中國城市規模增長滿足吉布拉定律;從時間跨度來看，9年及以上城市規模增長滿足吉布拉定律，這說明短期內城市規模增長可能不服從吉布拉定律，但從長期來看卻服從吉布拉定律。

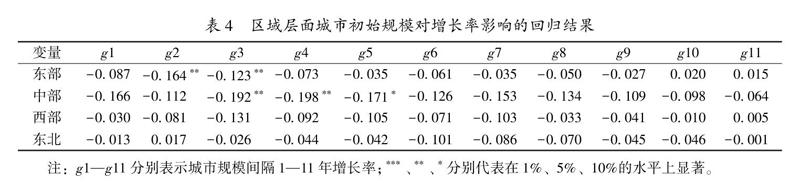
下面進一步分析區域層面城市初始規模對增長率的影響。表4報告了區域層面城市初始規模（2006年）對不同時間間隔增長率的回歸結果，其他年份城市的回歸結果備索。結果表明，東部、中部和西部地區少數年份的城市初始規模與增長率呈現顯著負相關或正相關，且這些增長率的時間間隔均在5年及以下，5年以上城市規模增長率與初始規模均不存在顯著性相關，這說明雖然短期內存在城市初始規模與增長率相關的事實，但是長期內城市規模增長與初始規模不存在相關性;東北地區城市初始規模與增長率均不存在顯著性相關。綜合來看，區域層面城市規模增長基本服從吉布拉定律。

2. 非線性模型估計

本文參考現有研究的做法[11-12，37]

建立非參數估計模型。

gi=m（pi）+εi（5）

其中，p為城市規模的自然對數，即p=lnP;m（pi）為利用pi估計所有p的回歸曲線，其估計值為m^（p），是圍繞p點的局部平均值，并使用對稱、加權和連續的核密度（如圍繞p對稱的連續加權函數）圍繞p進行平滑處理。基于哈德爾（Hrdle）提出的納達拉亞-沃森（Nadaraya-Watson）估計方法[38]，計算其條件均值：

m^（p）=n-1∑ni=1Kh（p-pi）gin-1∑ni=1Kh（p-pi）（6）

其中，K為核函數，本文采用埃帕內奇尼科夫（Epanechnikov）核函數[39];h為帶寬。

基于全國和區域層面城市規模與增長率的數據，采用500個樣本的自主法（bootstrap）和95%的置信區間進行非參數局部線性核回歸，其結果與表3和表4線性估計結果基本一致。由于篇幅受限，本文不再列出相應的回歸估計值，其結果備索。下面主要利用模型給出的城市增長率條件均值來分析其與城市初始規模的非線性關系，本文僅列出部分年份的非線性估計結果，如圖4所示，圖中虛線部分為95%的置信區間，該置信區間非常小，幾乎和模型曲線重合，但在圖4 2006—2017年圖中可以看出一點。

結果表明，2006—2010年城市規模增長率與2006年城市規模呈現“U”型關系，即隨著城市規模增加，增長率呈現出先下降后上升趨勢;30萬—1000萬人口城市的增長率為負值，且最小值在400萬人口城市左右。這說明對小城市而言，規模越小越有利于人口增長;中等城市和大城市規模越大越不利于人口增長;特大城市規模與其增長率雖呈現負相關，但卻呈現出逐漸減少的趨勢;超大城市規模與增長率呈現正相關，這與其人口集聚優勢密切相關。2010—2014年城市規模增長率與2010年城市規模呈現負相關，且40萬人口以上城市的人口增長率均為負值，但其人口增長率的下降幅度較小。這說明該期間內中等及以上規模城市的人口增長率呈現出微弱的下降趨勢。2014—2017年城市規模增長率與2014年城市規模呈現先上升后下降的倒“U”型態勢。具體來說，小城市規模增長率基本為零，中等城市和大城市的增長率與其規模呈現顯著正相關，而特大城市和超大城市具有顯著負相關，且超大城市具有負的人口增長率。這說明該時期內中等城市和大城市具有較高的人口增長率。從總體時間樣本2006—2017年來看，城市規模增長率與其初始規模呈現倒“N”型態勢，且10萬以下和200萬—1000萬人口的城市增長率為正值，40萬—200萬人口的城市增長率為負值。這說明考察期內小城市、大城市和特大城市具有較高的人口增長率，而中等城市和規模較小的大城市陷入人口增長停滯期。綜合來看，城市規模增長率與其初始規模并不存在明顯相關性，即服從吉布拉定律，這與上述分析基本一致。

3. 空間模型估計

如果城市規模存在不同程度的空間依賴性，采用上述估計方法也可能會存在偏誤。本文采用全局莫蘭指數考察城市規模及其增長率是否存在空間相關性，其中空間權重矩陣的元素取值為城市間地理距離的倒數。通常采用標準化統計量Z值來檢驗莫蘭指數的顯著性水平。結果表明：城市規模的莫蘭指數值在0.035—0.049之間且在統計上滿足1%的顯著性水平，這表明城市人口規模存在明顯的空間正相關，但空間關聯性不強;除城市規模間隔1年或2年增長率在個別年份不存在空間相關性外，其余城市規模增長率的莫蘭指數值在0.024—0.142之間且在統計上顯著，這表明城市增長率也存在一定的空間相關性。從時間維度來看，城市規模及其增長率的莫蘭指數值均呈現出上升趨勢，這充分說明城市規模的空間依賴性呈現增強態勢。基于此，本文構建空間計量模型如下：

gi=α+βpi+ρwijgi+εi（7）

其中，ρ代表空間回歸系數，w代表空間權重矩陣。

基于全國和區域層面城市規模與增長率的數據，采用空間計量模型考察城市初始規模對增長率的影響，其結果與線性回歸估計結果基本一致。由于篇幅受限，本文不再列出相應的回歸估計值，其結果備索。

上述分析均是基于截面數據的分析結果，而城市規模增長是一個連續過程，需要利用面板數據進一步考察。因此，本文構建衡量城市初始規模對其增長率影響的空間面板計量模型：

gi，t=βpi，t+ρ∑nj=1wijgi，t+θ∑nj=1wijpi，t+μi+ηt+εi，t，εi，t=λ∑nj=1wijεi，t+σi，t（8）

其中，λ代表空間誤差系數，θ代表基期城市規模的空間影響，μ代表個體效應，η代表時間效應。現有常用空間計量模型主要包括空間滯后模型（SAR）、空間誤差模型（SEM）和空間杜賓模型（SDM）三種形式，本文使用LR檢驗確定SAR模型、SEM模型或SDM模型類型，使用豪斯曼（Hausman）檢驗判斷固定效應或隨機效應。

表5報告了中國城市初始規模對不同時間間隔增長率的面板回歸結果。模型選擇中，LR檢驗結果表明所有模型均應選擇SDM模型;豪斯曼檢驗結果表明所有模型均應使用固定效應模型。回歸結果表明，除10年增長率模型外，各模型中空間回歸系數ρ均大于零且在統計上顯著，說明全國城市規模存在顯著為正的空間相關性，同時城市規模的空間項θ為正值且在統計上滿足1%的顯著性水平，說明周邊城市規模增加對本地城市規模增長速度具有顯著的促進作用，即空間外溢是促進城市規模快速增長的一個重要因素。所有模型中城市規模的回歸系數β均小于零且在統計上顯著，說明中國城市人口規模的增長率與初始規模呈現負相關，即城市規模較小的城市擁有較大的增長率，而城市規模較大的城市擁有較小的增長率。從時間趨勢來看，城市初始規模對其增長率的影響會隨著時間推移呈現出先上升后下降的趨勢，且對4年增長率的影響最大。綜合來看，中國城市規模存在顯著為正的空間相關性和空間外溢性，且與其增長率呈現顯著負相關。

五、結論與建議

本文基于2006—2017年中國628個城市規模數據，采用齊普夫定律和吉布拉定律分別檢驗城市規模分布和增長狀況，得出如下研究結論：中國城市規模分布基本服從齊普夫定律，這表明中國城市體系合理性較高;但存在明顯的分化特征和趨勢;中部地區城市規模分布呈現扁平化特征，而其他區域均存在明顯的分化特征和趨勢，這與中部地區城市規模差異較小有關;全國和區域層面城市規模增長基本服從吉布拉定律，這與小城市和大城市人口增長較快，而中等城市人口增長較慢相關;考慮到空間因素后，中國城市規模增長率與其初始規模呈現顯著負相關。

基于上述研究結論，得出如下政策建議：第一，科學認識城市規模的分布規律。中國城市規模體系比較合理，針對其日益明顯的分化趨勢，需要調整未來城鎮化戰略發展的重點，不僅要一如既往地重視大城市（尤其是特大和超大城市）發展，也應該重新重視中小城市發展，最終實現大中小城市協調發展。在現有資源配置不均衡情況下，人口向大城市集聚是用腳投票的結果，這就要求政府部門在制定政策時應該在充分考慮其資源稟賦和區位優勢的基礎上，明確其在國家和地區發展中的角色及定位功能，制定差異化措施保障實現城市發展，如中部地區應該注重大城市發展，通過加快承接東部地區制造業轉移等不斷增加大城市人口規模，以改變其城市體系扁平化特征;而其他地區要注重控制大城市規模，注重大中小城市協調發展。第二，充分重視城市人口規模的增長態勢。由于中等城市人口規模增長緩慢是導致中國城市體系不夠均衡的重要原因，這就要求政府在制定城市人口規模協調發展政策時一方面要加大對中等城市的政策傾斜，通過采取某些制度性措施保障中等城市實現人口快速增長，這不能僅僅依靠城市自身的經濟發展水平和質量的提升，也要注重吸引人口的優惠政策出臺或高質量的市政公用設施水平，以全面促進這些城市經濟健康發展;另一方面也要注重大城市的空間溢出效應，增強大城市的空間溢出能力，這既可以一定程度上緩解某些城市由于人口過度集聚所產生的城市病問題，又可以強化其對周圍城市的輻射力，實現區域人口協同發展和構建合理化城市體系。

參考文獻：

[1]ZIPF G K. Human behavior and the principle of least effort[M]. Cambridge， MA： Addison-Wesley， 1949：364-376.

[2]GONZLEZ-VAL R， LANASPA L， SANZ-GRACIA F. Gibrats law for cities， growth regressions and sample size [J]. Economics Letters， 2013，18（2）： 367-369.

[3]KRUGMAN P. Confronting the mystery of urban hierarchy[J]. Journal of the Japanese and International Economics， 1996， 10（23）： 399-418.

[4]ROZENFELD H D， RYBSKI D， GABAIX X， MAKSE H A. The area and population of cities： new insights from a different perspective on cities[J]. American Economic Review， 2011， 101（5）： 2205-2225.

[5]BERRY B J L， OKULICZ-KOZARYN A. The city size distribution debate： resolution for US urban regions and megalopolitan areas[J]. Cities， 2012， 29（1）： 17-23.

[6]ROSEN K T， RESNICK M. The size distribution of cities： an examination of the Pareto law and primacy[J]. Journal of Urban Economics， 1980， 8（2）： 165-186.

[7]BLACK D， HENDERSON J V. Urban evolution in the USA[J]. Journal of Economic Geography， 2003， 3（4）： 343-372.

[8]NITSCH V. Zipf zipped[J]. Journal of Urban Economics， 2005， 57（1）： 86-100.

[9]SOO K T. Zipfs law for cities： a cross-country investigation[J]. Regional Science and Urban Economics， 2005， 35（3）： 239-263.

[10]GABAIX X. Zipfs law for cities： an explanation[J]. Quarterly Journal of Economics， 1999， 114（3）：739-767.

[11]IOANNIDES Y， OVERMAN H. Zipfs law for cities： an empirical examination[J]. Regional Science and Urban Economics， 2003， 33（2）： 127-137.

[12]EECKHOUT J. Gibrats law for （all） cities[J]. American Economic Review， 2004， 94（5）： 1429-1451.

[13]LEVY M. Gibrats law for （all） cities： comment[J]. American Economic Review， 2009， 99（4）： 1672-1675.

[14]IOANNIDES Y， SKOURAS S. US city size distribution： robustly Pareto， but only in the tail[J]. Journal of Urban Economics， 2013， 73（1）： 18-29.

[15]GONZLEZ-VAL R， LANASPA L， SANZ-GRACIA F. New evidence on Gibrats law for cities[J]. Urban Studies， 2014， 51（1）： 93-115.

[16]GIESEN K， ZIMMERMANN A， SUEDEKUM J. The size distribution across all cities： double Pareto lognormal strikes[J]. Journal of Urban Economics， 2010， 68（2）： 129-137.

[17]高鴻鷹，武康平. 我國城市規模分布Pareto指數測算及影響因素分析[J]. 數量經濟技術經濟研究，2007（4）：43-52.

[18]GANGOPADHYAY K， BASU B. City size distributions for India and China[J]. Physica A： Statistical Mechanics and Its Applications， 2009， 388（13）： 2682-2688.

[19]張車偉，蔡翼飛. 中國城鎮化格局變動與人口合理分布[J]. 中國人口科學，2012（6）：44-57.

[20]ANDERSON G， GE Y. The size distribution of Chinese cities[J]. Regional Science and Urban Economics， 2005， 35（6）： 756-776.

[21]LUCKSTEAD J， DEVADOSS S. A comparison of city size distributions for China and India from 1950 to 2010[J]. Economics Letters， 2014， 124（2）： 290-295.

[22]梁琦，陳強遠，王如玉. 戶籍改革、勞動力流動與城市層級體系優化[J]. 中國社會科學， 2013（12）：36-59.

[23]李松林，劉修巖. 中國城市體系規模分布扁平化：多維區域驗證與經濟解釋[J]. 世界經濟，2017（11）：146-171.

[24]鄧智團，樊豪斌. 中國城市人口規模分布規律研究[J]. 中國人口科學，2016（4）：48-60.

[25]魏守華，孫寧，姜悅. Zipf定律與Gibrat定律在中國城市規模分布中的適用性[J]. 世界經濟，2018（9）：98-122.

[26]ZENG C， ZHOU Y， WANG S， et al. Population spatialization in China based on night-time imagery and land use data[J]. International Journal of Remote Sensing， 2011， 32（24）： 9599-9620.

[27]吳健生，劉浩，彭建，馬琳. 中國城市體系等級結構及其空間格局——基于DMSP/OLS夜間燈光數據的實證[J]. 地理學報，2014（6）：759-770.

[28]HUANG Q X， HE C Y， GAO B， et al. Detecting the 20 year city-size dynamics in China with a rank clock approach and DMSP/OLS nighttime data[J]. Landscape and Urban Planning， 2015， 137（1）： 138-148.

[29]JIANG B， YIN J， LIU Q. Zipfs law for all the natural cities around the world[J]. International Journal of Geographical Information Science， 2015， 29（3）： 498-522.

[30]魏守華，周山人，千慧雄. 中國城市規模偏差研究[J]. 中國工業經濟，2015（4）：5-17.

[31]陸銘，高虹，佐藤宏. 城市規模與包容性就業[J]. 中國社會科學，2012（10）：47-66.

[32]唐為. 中國城市規模分布體系過于扁平化嗎？ [J]. 世界經濟文匯，2016（1）：36-51.

[33]孫斌棟，金曉溪，林杰. 走向大中小城市協調發展的中國新型城鎮化格局——1952年以來中國城市規模分布演化與影響因素[J]. 地理研究，2019（1）：75-84.

[34]DAGUM C. A new approach to the decomposition of the Gini income inequality ratio[J]. Empirical Economics， 1997， 22（4）： 515-531.

[35]GABAIX X， IBRAGIMOV R. Rank-1/2： a simple way to improve the OLS estimation of tail exponents[J]. Journal of Business and Economic Statistics， 2011， 29（1）： 24-39.

[36]GONZLEZ-VAL R. US city size distribution and space[J]. Spatial Economic Analysis， 2019， 14（3）： 283-300.

[37]GONZLEZ-VAL R. The evolution of U.S. city size distribution from a long-term perspective （1900-2000） [J]. Journal of Regional Science， 2010， 50（5）： 952-972.

[38]HRDLE W. Applied nonparametric regression[M]. Cambridge， New York and Melbourne： Cambridge University Press， 1990： 32-33.

[39]EPANECHNIKOV V A. Nonparametric estimations of a multivariate probability density [J]. Theory of Probability & Its Applications， 1969，14（1）： 153-158.

[責任編輯 武 玉]