偏正態數據下眾數混合專家回歸模型的參數估計
王格格,魯鈺,吳劉倉
(昆明理工大學理學院,云南昆明650504)
1.引言
在我們的現實生活中收集到的數據大多數都不具有嚴格的對稱性,而是具有一定的偏斜,如果我們繼續用對稱分布比如:正態分布、t分布、Laplace分布等進行統計推斷可能會得到不合理甚至錯誤的結論.因此,對偏態數據的統計推斷成為統計學研究的一個熱點問題.在偏態數據中,眾數比均值、中位數應用更為廣泛,在總體中,眾數標志著出現次數最多,它刻畫了總體數據集中趨勢的大多數水平.為了更好地擬合偏態數據,捕捉到更全面、更準確、更及時有效的信息,本文針對偏正態分布建立了眾數回歸模型,進一步拓展了偏正態分布下眾數混合專家回歸模型.
偏正態分布作為正態分布的推廣,不僅具有正態分布的良好統計特性,同時也有具有偏態分布的特征,適用性更廣泛,所以國內外許多學者研究了偏正態分布問題.Azzalini[1]首先研究了偏正態分布及其累積分布函數和概率密度函數的性質;萬文等[2]研究了偏正態分布下聯合位置與尺度模型的統計診斷;馬婷等[3]研究了基于偏正態分布聯合位置,尺度與偏度模型的極大似然估計;朱志娥等[4]在未對混合比例建模的情況下,研究了偏t正態數據下混合線性聯合位置與尺度模型的參數估計;Lachos等[5]在多元偏正態回歸模型上,基于EM算法構建多元偏正態回歸模型的極大似然估計;在變量選擇方面,吳劉倉等[6]基于偏正態分布研究了聯合位置與尺度模型的變量選擇問題;LI和WU等[7?8]分別基于SN、StN分布,對聯合位置、尺度和偏度模型的參數估計和變量選擇做了研究.但上述研究僅對偏正態分布或偏正態分布的位置和尺度進行建模,沒有考慮數據來自異質性群體.
在經濟金融、環境工程、生物醫學等領域的實際問題中,經常遇到異質總體數據.數據越來越復雜對統計建模有更高要求,傳統的單一模型難以對異質總體數據得到較好的擬合效果,因此發展了混合回歸模型.在異質總體中,混合專家回歸模型是最重要的統計分析工具之一,用來對異質總體數據進行分類及回歸分析,在統計機器學習方面應用廣泛.混合專家回歸模型首先由Jacobs等[9]提出,對部分密度函數建模的同時,還對混合比例進行建模;隨后,Yuksel[10]對混合專家模型及其性質進行了詳細的描述;最近,Chamroukhi等[11]針對混合回歸專家模型提出了一種基于t分布的穩健模型;吳劉倉等[12]研究了基于偏正態分布下聯合位置與尺度混合專家回歸模型的參數估計.
目前,基于偏態數據和混合專家回歸模型的研究現狀可以發現,雖然偏正態分布和混合專家回歸模型都已經有了很多的研究成果,但在混合專家回歸模型的框架下對偏態數據下眾數建模涉及較少.考慮到混合專家回歸模型在實際問題應用中的重要性,本文建立了偏正態分布下眾數混合專家回歸模型,并對該模型進行參數估計,通過隨機模擬和實例結果表明本文提出的模型是具有可行之處的.
本文的組織結構安排如下:第二部分分別介紹了偏正態分布、偏正態分布下眾數回歸模型及其混合專家回歸模型;第三部利用MM算法和基于梯度下降法的EM算法分別對各個模型的參數進行估計;第四部分通過MonteCarlo模擬證實本文提出方法的有效性;第五部分使用了澳大利亞身體質量指數(BMI)數據中的一個實際例子來說明本文提出的模型和方法的效果;最后是本文的小結部分.
2.偏正態分布下眾數混合專家回歸模型



圖1.混合數目為2的混合專家回歸模型


3.參數估計





III 確定混合數目
在上面的討論中,我們假設m是已知的,處理方法要么是基于先驗信息,要么是對數據進行預分析.可逆跳躍馬爾科夫鏈蒙特卡羅(RJMCMC)(見文[20])是一種可行的算法,由于增加了偏度使算法變得復雜,我們沒有繼續使用RJMCMC.此外,貝葉斯推斷混合建模中評估的成分后驗概率可以用作一種軟聚類方案.另外,可以使用對數似然估計和兩個基于信息的準則,AIC[21]和BIC[22]來確定混合數目.眾所周知,模型選擇標準方面已經取得了一些成功,但為混合模型選擇正確的混合數目是有一定困難的.
為了提高本文選擇混合數目的效率,采用了一種通過眾數識別的生產性聚類方法[23].這種方法在高維空間和數據的分布偏離高斯分布的情況下是穩健的.具體來說,這些樣本點上升到密度函數的同一局部最大值形成一個聚類,并利用兩個聚類密度凸點之間的脊線定義了聚類的兩兩可分性測度.在此過程中,采用模態EM(MEM)算法和脊線EM(REM)算法.水平5時集群數量依次為37、10、4、2、1.我們在第5節中演示了水平2和水平4時的聚類結果.
4.Monte Carlo模擬


表1.模擬估計結果
從表1可以得出結論,隨著樣本量n增大,參數估計值均越來越接近真值,且估計的均方誤差MSE均逐漸減小,說明樣本量越大估計效果越好.
5.實例分析
現實生活中,我們通常要根據研究對象的特征對其進行聚類分析,如果只是對樣本進行總體上的分析,得到的結果可能是不準確的,如果能將總體分成具有相似特征的若干個子聚類,對每個子聚類進行分析,得到的結果可能比僅對總體分析更接近實際.在本節中,我們利用澳大利亞體育研究所收集的100名女性和102名男性運動員的體質指數(BMI)數據來說明本文提出模型和方法的實際應用.
人體體質指數由身高和體重計算得到的,但跟身體其它機能有密切關系,該數據包含一個響應變量Y ?體質指數(BMI)和四個解釋變量:X1?白細胞計數;X2?血漿鐵蛋白濃度;X3?皮膚褶皺總和;X4?體脂百分比.總數據的BMI直方圖(見圖2)是右偏的,如果我們用正態分布來擬合,會有一些樣本點被視為異常值,因此,我們使用本文所提出的模型和方法進行深入分析.我們通過3.3節的方法來確定混合的數目,結果如圖3所示.當處于水平2時,形成了10個集群,如圖3(a)所示.圖3(b)和(d)為水平2時的10個集群在水平3時合并為4個集群.與水平4時相比,水平3的第1類和第2類中排除了兩個有影響的觀察結果.這里,水平2時的10個集群其對應的大小(包含的點的數量)分別是95、48、33、18、3、1、1、1、1、1.為簡單起見,我們考慮以下模型:
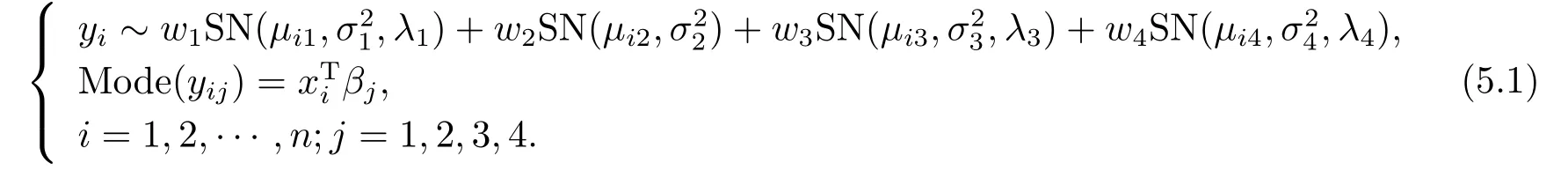
其中,μij由(2.7)定義.xi是一個4×1 向量,由所有4個潛在變量組成.
我們采用本文介紹的梯度下降法輔助的EM算法得到參數估計的最大值,結果見表2.顯然,含四個成分的模型的對數似然估計最大,AIC和BIC值最小,所以這個模型是最優的.模型在水平2時,體脂百分比(x4)在第2組和第4組中更易獲得較高的BMI指數,血漿鐵蛋白濃度(x2)只在第1組中有助于達到較高的BMI指數.
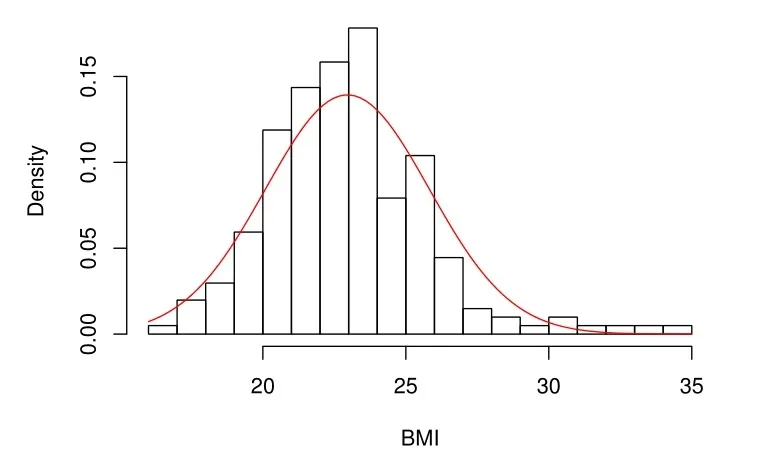
圖2.總體數據的BMI直方圖

圖3.對獲得的BMI數據聚類;(a)為水平2時聚成10類;(b)為從水平2到水平3時的上升路徑;(c)為水平3時聚成5類;(d)為水平3到水平4時的上升路徑;(e)為水平4時聚成2類;(f)為水平4到水平5時的上升路徑
6.結論
本文建立偏正態分布下眾數混合專家回歸模型,目的是估計異質總體的不同回歸參數,而不是對總體參數的單一估計.并且對混合比例建模,對影響混合比例的解釋變量有一定了解,在實例中有很好的體現.
Monte Carlo模擬表明本文提出的MM算法和梯度下降法輔助的EM算法對偏正態分布下眾數混合專家回歸模型未知參數進行了較好的估計.與現有的模型和估計方法相比較,提出模型有較好的靈活性,不僅把各異質總體所占比例估計出來,同時也能估計異質總體的回歸參數.此外,為確定混合數目,我們采用文[23]提出的方法來聚類,取得了良好的性能.表明,本文提出的模型和方法是有效可行的.
- 應用數學的其它文章
- Global Boundedness and Asymptotic Behavior in a Chemotaxis Model with Indirect Signal Absorption and Generalized Logistic Source
- 一類基于梯度下降的高效分布式計算方法的應用研究
- 通脹風險和最低保障約束下基于二次效用函數的DC型養老金最優投資策略
- 三維不可壓磁微極流的投影統計解及其退化正則性
- Dynamic Feedback Stabilization for Timoshenko Beam with Locally Input Controls and Input Distributed Delay
- 一類奇異拋物方程淬火解的數值分析

