工程擾動下礦山高陡邊坡力學響應規律研究

賈新昆 盧邦飛

（天津華北地質勘查局，天津300170）

隨著現代露天采礦工藝技術與安全科學的發展，越來越多的礦床能夠滿足新環境下的露天開采條件。然而，隨之產生了大量的高陡邊坡與凹陷露天深坑，受區域環境影響，加上開采過程中各種生產擾動，使得邊坡構造發生變化，在開采工作區周圍出現一系列力學現象或巖層內部損傷，進而可能導致崩塌、滑坡、地面塌陷、泥石流及不穩定斜坡等地質災害［1］。如何在保證礦石開采的同時，兼顧邊坡與露天坑整體穩定性，有效防止自然與人為因素對邊坡穩定性的破壞，是露天采場安全高效生產的重中之重。近年來，我國金屬非金屬礦山露天開采深度增長明顯，一方面由于露天開采本身存在諸多安全高效的優點，另一方面我國露天開采技術也在逐步成熟與進步，機械化和深孔穿鑿爆破工藝技術等方面均有長足的發展［2］。同時，隨著土地復墾與露天礦二次開發的廣泛推行，我國礦業未來將以實現“綠色采礦，無廢開采”［3］為目標。然而，隨著露天采礦逐步向深部發展，高陡邊坡與深凹露天坑的增加，造成了大量的安全隱患。我國安全環保管控力度正逐步加大，工程擾動下的露天礦邊坡穩定性研究也逐步成為重要的科研課題［4］。

從國內現有成果來看，對邊坡穩定性研究所采用的方法主要有彈性理論、承壓理論，現行的相關理論也重點圍繞這些方法來展開應用研究。安全系數是邊坡穩定性分析與評價的關鍵指標，其來源主要是依據邊坡體的強度與本構特性。相似模型模擬、有限元、離散元、邊界元等數值分析模擬方法理論以及現場實測分析等方法，是當前邊坡穩定性分析的常用方法。其中，劉暢［5］提出了“轉動滑坡”、“結構面控制”、“空洞的影響”及“差異沉降”這4種構想；劉殿柱［6］利用Matlab軟件對有代表性的數據進行頻域分析及回歸分析處理，總結了高陡邊坡的爆破振動特點及爆破振動衰減規律；董英健等［7］以露天礦開采為例，對露天邊坡爆破開采的危險源進行了分析，并提出了露天礦山爆破安全的預防和治理措施；嚴鵬等［8］通過回歸分析建立了不同爆心距處質點峰值振動速度與損傷深度的關系；胡英國等［9］針對預裂爆破等兩種不同方式，應用LS-DYNA軟件平臺進行二次開發，成功模擬仿真出損傷時變效果，得出巖石高陡邊坡在2種開挖方式下最終保留巖體的損傷分布特征；楊天鴻等［10］基于國內外邊坡穩定性研究成果，結合“邊坡巖體漸進損傷破壞是邊坡巖體失穩前兆本質特征”這一思路，提出了露天礦邊坡巖體強度參數識別表征方法和動態穩定性評價方法。然而，隨著開采深度逐年增加，傳統分析方法難以解決高陡邊坡的復雜問題，針對應力、位移和塑性區的穩定性分析方法比較簡單，且大多側重考慮單方面因素對邊坡穩定性的影響，缺乏多方面的分析，因而存在一定的不合理性。

針對某露天礦山高陡邊坡復雜多因素影響導致滑坡、泥石流以及大范圍崩塌的工程實際［11］，在研究高陡邊坡穩定性分析相關理論的基礎上，結合相關邊坡優化理論，綜合考慮區域地質條件，建立邊坡穩定性分析的三維數值模型，并從應力遷移與動力擾動相結合的角度進行分析，以安全生產與環境保護為目標，開展露天礦山高陡邊坡穩定性優化研究。

1 高陡邊坡工程技術條件

露天采場平面呈橢圓形，長軸寬度與短軸寬度分別為646 m和601 m。巖性以似斑狀二長花崗巖為主，剝離后露天采場邊坡角為55°，隨著開采的推進，在區域內形成了高陡邊坡。本研究所選計算區域為礦區1號采坑，根據境界圈定原則和邊坡參數，確定+315 m以上為山坡露天開采，+315 m以下為凹陷露天開采。露天采場規劃布置采用螺旋形坑線，布置在各采坑邊幫上，形成環形固定坑線，如圖1所示。原采坑按順時針方向下降展線，至坑底+60 m標高平臺。1號采坑按逆時針方向下降展線，至坑底+35 m標高平臺。采坑預計最終深度將到達300 m，為礦山最突出的高陡邊坡露天采坑，因此針對這一區域展開研究具有代表性。通過圈定露天境界，獲得開采境界尺寸數據為臺階高度15 m，坡面角65°，邊坡角43°～47°。1號采坑邊坡角為45°～46°

數值模型以1號采坑境界圈定為依據，其尺寸為：上部長1 167 m，寬894 m，底部長338 m，寬254 m，頂部標高+375 m，當前底部標高+190 m。采坑內部使用穿孔作業，每日3班，干孔采用乳化粉狀炸藥，水孔采用漿裝乳化炸藥，鉆孔采用“Ⅴ”形布置，采用非電導爆管排間微差起爆的松動爆破方式。礦山一次爆破作業量見表1。

爆破動力數值模擬選取的深凹高陡邊坡研究區域如圖1所示，其邊坡輪廓線與滲流分析模型一致，均為高陡邊坡。

2 顯式—隱式分析模型聯合構建

2.1 顯式—隱式算法轉換

顯—隱結合的計算模型需要借助ANSYS與LSDYNA仿真軟件平臺。ANSYS軟件靜力學隱式分析的主要原理是通過迭代法解方程組，這種方程組是非線性的，對變形比較小的問題求解效果較好；但對于大變形的求解精度將會降低很多，且收斂性一般。其求解方法的優點在于，時間步長可調范圍大，計算精度與整體計算過程并行，迭代次數越多，精度也越高。一般來說，數值模擬的計算時間成本大多與自由度數目緊密相關。LS-DYNA軟件以顯式分析見長，屬于非線性計算軟件，但還具有隱式分析功能。顯式分析的特點是需要考慮時間，即計算過程中需要對時間進行差分，因此不存在多次迭代后不收斂的問題，其最小時間步長受最小單元尺寸控制。

為了在高陡邊坡動力穩定性分析中考慮地應力的影響，如果在LS-DYNA軟件中施加載荷則該變量具備時變性，因此計算過程中荷載會隨時間一直持續下去，與現實情況不符。故通過ANSYS軟件計算地應力時，待地應力收斂后，將地應力數據文件導入LS-DYNA軟件中進行爆破動力計算［12-13］。顯式—隱式分析的主要步驟如圖2所示。

首先根據礦山實測邊坡剖面建立邊坡坡體數值模型，劃分網格并賦予材料參數，求解獲得地應力分布結果；然后清理邊坡體上部覆蓋的巖土體，即進行開挖，獲得土體剝離后的高陡邊坡應力分布結果。靜力學計算結束之后更改工作名，再保存文件。如果沒有此項操作，在完成顯式求解后，隱式結果文件會被覆蓋。隱式分析與顯式分析單元類型有所不同，隱式分析時采用的是3D solidf185單元，在進行爆破動力分析時一般采用3D solid164顯式單元。工作名更改完成后選取“隱式—顯式轉換”模式并確認，即完成單元類型轉換。在隱式求解設置過程中，邊界條件設置與顯式邊界條件有很大區別。故轉換到顯式設置界面后需將多余的邊界條件去除，再添加顯式動力求解所需的邊界條件。此步驟是顯隱轉換的關鍵，顯式設置界面通過讀取該文件進行顯隱計算關聯。

Drelax文件中的位移和轉動被賦值于顯式分析結構中，并且考慮了計算前期收斂的地應力預荷載。“Dynamic relax”命令指示LS-DYNA軟件求解器使用動力松弛進行應力初始化。靜態分析在虛擬時程上進行，在時間步內，所有動能由阻尼消除。在進行顯式分析時，需要定義時間相關變量，設置完后生成K文件，修改巖石及炸藥材料參數保存為最終K文件。調用LS-DYNA Solver，遞交K文件進行求解。

2.2 材料參數及模型構建

將邊坡模型導入ANSYS軟件中，顯式動力學計算時由于施加了爆破載荷，在模型相應邊界需施加無反射邊界條件來模擬無限大區域，消除應力波反射作用對分析結果的影響。對于無反射邊界條件的施加，三維單元較二維單元更為方便快捷，僅需選擇邊界節點建立節點組，通過命令施加即可。考慮到二維與三維模型各自優點，建立了準二維數值模型，即在Z方向僅取一個單位長度20 cm，并且在Z方向施加位移約束，有利于選取邊界節點建立節點組施加無反射邊界條件。

材料模型采用MAT_PLASTIC_KINEMATIC材料模型［14-15］，該模型考慮了彈塑性力學特征。在應力未到達屈服應力前，應力與應變之間通過楊氏模量系數E進行關聯，應力超過屈服點后，應力—應變關系通過小于楊氏模量的切線模量系數Et進行關聯，其本構模型如圖3所示，圖中l0與l表示試件單軸壓縮時的未變形及變形后的長度。

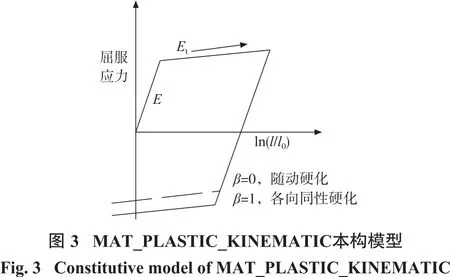
圖3中所示硬化參數β在[0 ,1]區間內取值，對應的材料特性為：隨動硬化模型β=0，混合硬化模型0＜β＜1，各向同性硬化模型β=1。等向強化模型假定材料在塑性變形后，仍保持各向同性性質，忽略了由于塑性變形引起的各向異性的影響，模擬中將巖石視為隨動硬化模型（β=0）。巖石材料本構模型為

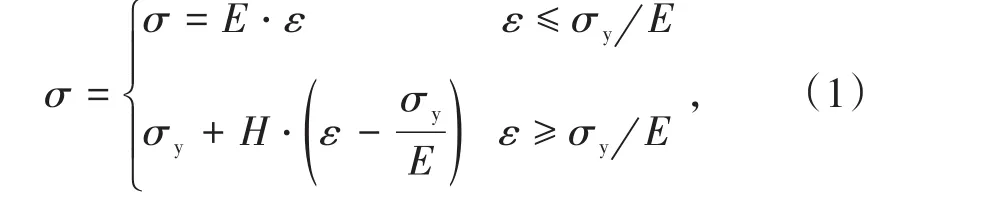
式中，σ為應力，GPa；ε為應變；E為彈性模量，GPa；σy為屈服應力，GPa；H為應變硬化指數，Et為切線模量。

巖石物理力學參數取值見表2。

模型一般采用高爆材料模型與JWL狀態方程來定義［16-17］。ANSYS軟件中并無該材料模型，需采用其它材料定義，在K文件中手動添加相關關鍵字來賦值材料參數。LEE于1965年在JONES和WILKINS工作的基礎上提出了JWL方程［18］：

式中，P為爆轟壓力，MPa，V為相對體積；Ev為單位體積內能，J/m3；ω，A，B，R1，R2為材料參數。巖石炸藥材料參數取值見表3。

注：LS-DYNA單位制采用cm-g-μs。

在邊界條件方面，顯式與隱式分析的邊界條件有所不同。模型靜力分析的邊界條件采用定向位移約束，坡面邊界忽略地表起伏，設定為自由面。轉換為動力分析界面后，邊坡上覆巖體已經剝離，左右邊界及下邊界增加溢出邊界條件，藥包模型布置在邊坡最低臺階位置。

3 模型運算及工程應用

3.1 動靜耦合力學分析

3.1.1 靜力狀態

在開挖前，初始應力采用自重應力加載和單元清除的方式生成，水平應力均勻設置，且應力值隨深度增加而增加。初始應力計算過程中采用線彈性材料，故無塑性區形成［19］。模型選取的高陡邊坡區域長210 m，高180 m，清除單元總數為13 329個。初始應力計算結果如圖4和圖5所示。

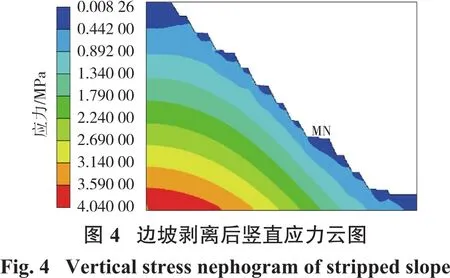
邊坡上部單元剝離后產生卸荷力學作用，由于上層巖體約束被解除，邊坡面形成了部分回彈效應，坡面應力值驟減。模型下邊界應力值逐級減小，也是由于失去上覆壓力造成的。高應力區主要集中在邊坡體原點位置，低應力區主要分布在坡面。當受到劇烈爆破振動影響時，坡面會率先發生動力響應，且極易發生破壞。因為在這一階段，邊坡面已形成自由面，爆破波傳來時有足夠的自由震蕩空間，當邊坡坡面振動速度超過巖體承載臨界值時即發生破壞。

3.1.2 動靜耦合穩定性分析

目前深孔臺階爆破法已經成為露天礦生產爆破的主要方法。邊坡體自由面較大，在動力擾動下振動波在坡面極易產生反射。邊坡上覆巖體剝離之后形成高陡邊坡體，形成的臨空面越高其危險系數也越大。隨著生產裝藥量不斷增加，邊坡體承受的動力擾動強度也隨之增大，其穩定性面臨嚴峻挑戰，故有必要對動靜耦合作用下的邊坡體動力響應規律進行研究。為了考慮整個邊坡體的應力場影響，動力分析時需要建立完整模型。如果爆破載荷依據實際的炮孔尺寸進行施加，則炮孔尺寸與邊坡尺寸相差較大，不利于模型構建以及網格劃分，因此需要將單孔裝藥等效為裸露藥包模型。由于邊坡上方生產工作已經結束，上部邊坡即為最終邊坡，根據模型設定將裸露藥包置于露天坑最底部。本次分析的藥包尺寸為100 cm×100 cm×20 cm（長×寬×高），等效藥量為250 kg。由于動力穩定性分析過程中爆破載荷要與邊坡體地應力耦合，故列出應力云圖進行對比分析。將隱式分析結果導入LS-DYNA軟件后的應力云圖存在細微差異，主要原因是因為計算原理不同，但邊坡體整體應力分布保持了較好的一致性，故在爆破動力分析中通過顯式—隱式轉換導入地應力的方法是可行的。

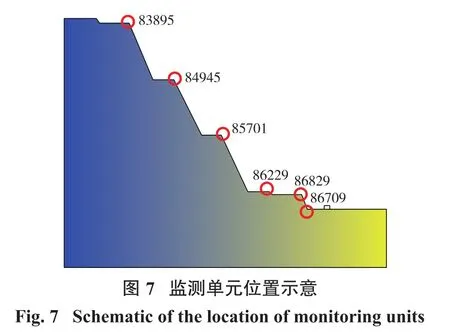
藥包起爆時刻設定為0時刻，起爆后能量以波的形式向巖體內傳播（圖6）。由于藥包附近巖體表面較為平整，故爆破應力波以同心圓弧的形式向下傳播。當應力波遇到下邊界及右邊界時，受無反射邊界條件影響，應力波在此界面發生透射。另一側應力波沿介質傳遞，藥包近區巖體處于高應力加載狀態。另一方面，邊坡體坡頂、平臺與坡面均為自由面，應力波傳播到上述位置將發生分散并疊加，故后續應力云圖出現不規則波動。隨著應力波繼續傳遞，能量逐漸耗散。為定量研究邊坡體受爆破載荷的影響，對臺階邊界單元的應力時程響應結果進行了監測，單元位置如圖7所示，各監測單元標高自上而下依次為+205、+135、+60、+50、+35 m。

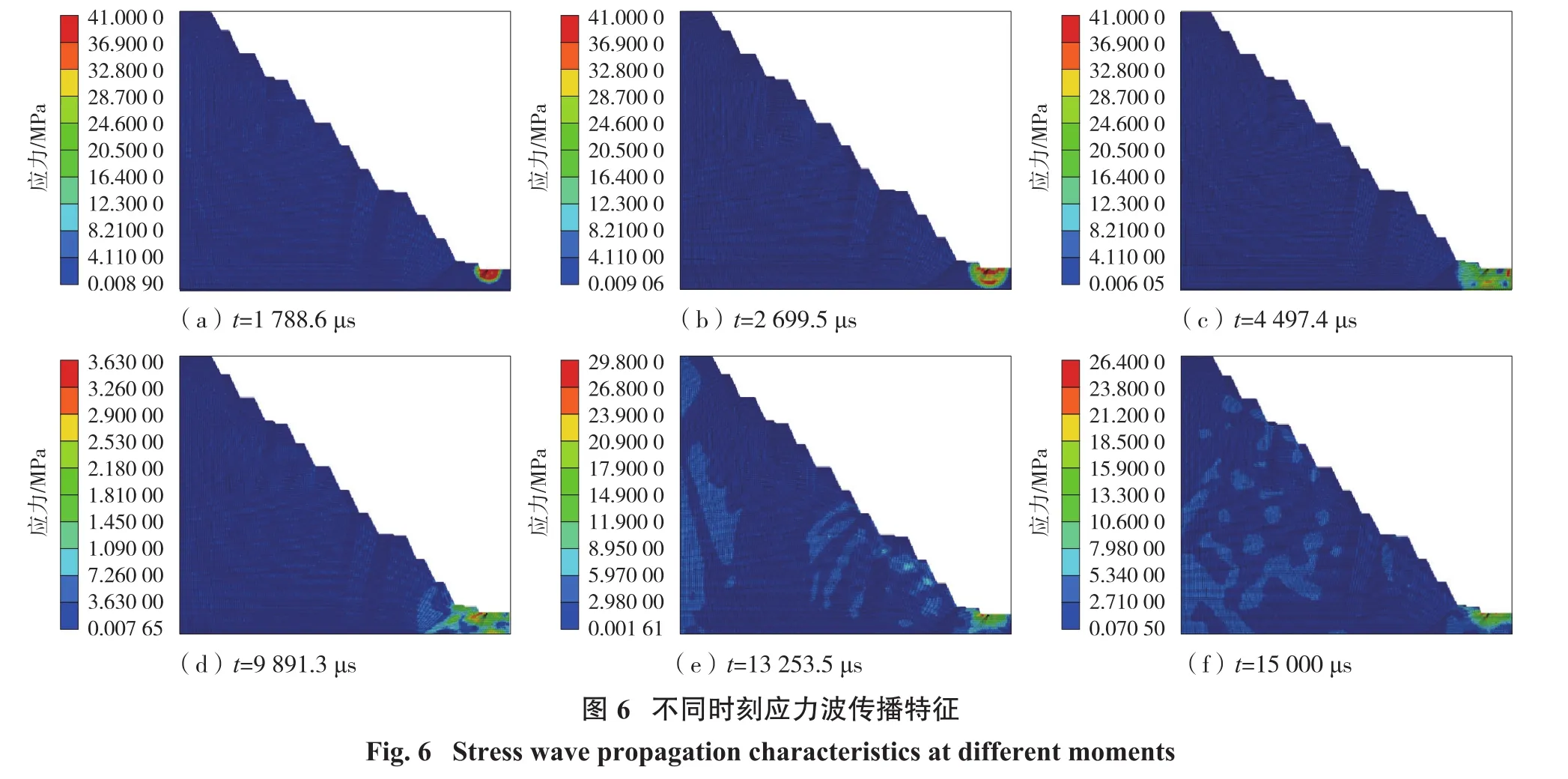
各單元應力—時程曲線如圖8所示。分析圖8可知：距離藥包最近的86709單元率先發生響應，其應力值比其它4個單元高。86709單元動力響應不同于其他單元，故需進行單獨監測。隨著卸荷狀態起步，86709單元初始應力為0.938 MPa，受到爆破應力波作用后應力迅速下降，直至應力方向改變為Y反向。此后應力值發生波動，在7 190 μs時刻應力絕對值達到峰值40.8 MPa，此后應力波不斷震蕩并衰減。所有單元都是在初始應力影響下發生動力響應，在爆破應力波影響下呈現卸荷狀態。各監測單元的應力極值如表4所示。

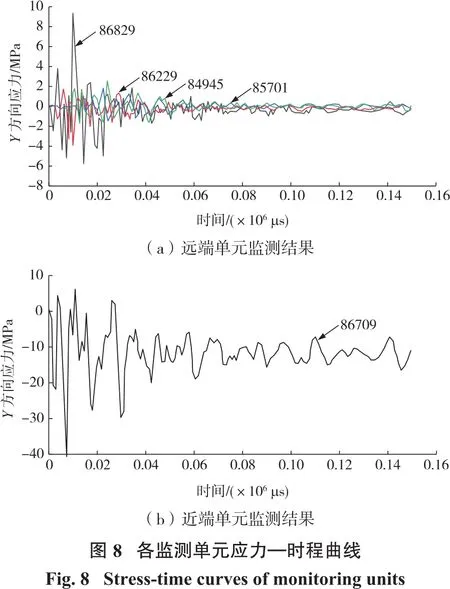
結合表4分析可知：最遠兩個單元相距50 m，應力極值隨著影響距離的增加而減小，最遠的84945單元的應力極值僅為1.9 MPa。從響應程度分析，爆破對邊坡的影響主要集中在86829單元所在臺階。由于藥包是裸露安放，因此初始爆破能積蓄較小。

對邊坡體響應分析的依據，除了有效應力監測結果外，也可采用質點振動速度來衡量。坡面及臺階均為自由面，故振動比較明顯，本研究主要從質點振動速度變化來分析，對5個關鍵節點的振動速度進行監測，監測點位置如圖9所示。

各測點的最大振動速度監測結果如表5所示。由表5可知：該當量藥量測點振動速度極大值均高于安全規程規定范圍。測點上邊界及右邊界均為自由面，屬于典型的卸荷自由面。應力釋放后該位置應力值較小，質點具有相對自由的響應空間。測點振動速度較高，其原因除了炸藥量較高外，監測點位于邊坡頂部自由面，應力波反射作用較強也是關鍵因素。實際生產中，邊坡開挖過程經歷長時間卸荷作用，特別是坡頂位置巖土體處于松散狀態，當受到爆破振動影響時，邊坡坡面經常有砂石滾落。

根據應力以及測點振動速度綜合分析可知，邊坡體總體穩定性較好，受爆破動力影響，坡頂位置質點振動速度較大，生產中易掉落碎石，需重點防范。隨著節點位置變化，爆心距也在增加，若在完整巖體中，距離爆源位置越遠，爆破能量逐漸衰減，質點振動速度隨之下降。在工程實踐中，爆破引起的質點振動速度會隨著測點與爆心高程差的增加而增大，這一現象稱之為高程放大效應。這種效應受多方面因素控制，比如巖土體完整性、不良地質構造、爆破規模等。正常情況下，質點振動速度與爆心距、高程、開挖深度呈反比關系。高程放大效應也具有一定范圍，超過這個范圍就會消失，恢復正常狀態。X方向振動速度監測結果顯示，28592點位小于28576點位，對于Y方向振動速度，28599點位小于28592點位，這就是典型的高程放大效應，說明本研究仿真分析結果具有可靠性。通過動靜耦合分析可知，爆破振動效應與坡度大小緊密相關，在過爆心的坡面、邊坡、坡面角平分線圍成的區域內較為明顯。如果坡度大于1∶2，高程放大效應才會出現，坡面的自由反射作用也會影響坡體的振動頻率。

3.2 邊坡動力響應規律

上述分析僅對固定藥量作用下的邊坡體動力響應規律進行了分析，在實際生產中每次爆破量均不相等，故有必要對不同藥量爆破作用下的邊坡體動力響應規律進行研究。采用的計算方法仍為考慮地應力作用的顯式—隱式轉換法，共設定4組模型，如表6所示。圖10所示為不同藥量下的邊坡塑性變形情況，隨著藥包藥量增加，塑性區范圍不斷增大，不同方案對應的塑性區尺寸見表7。

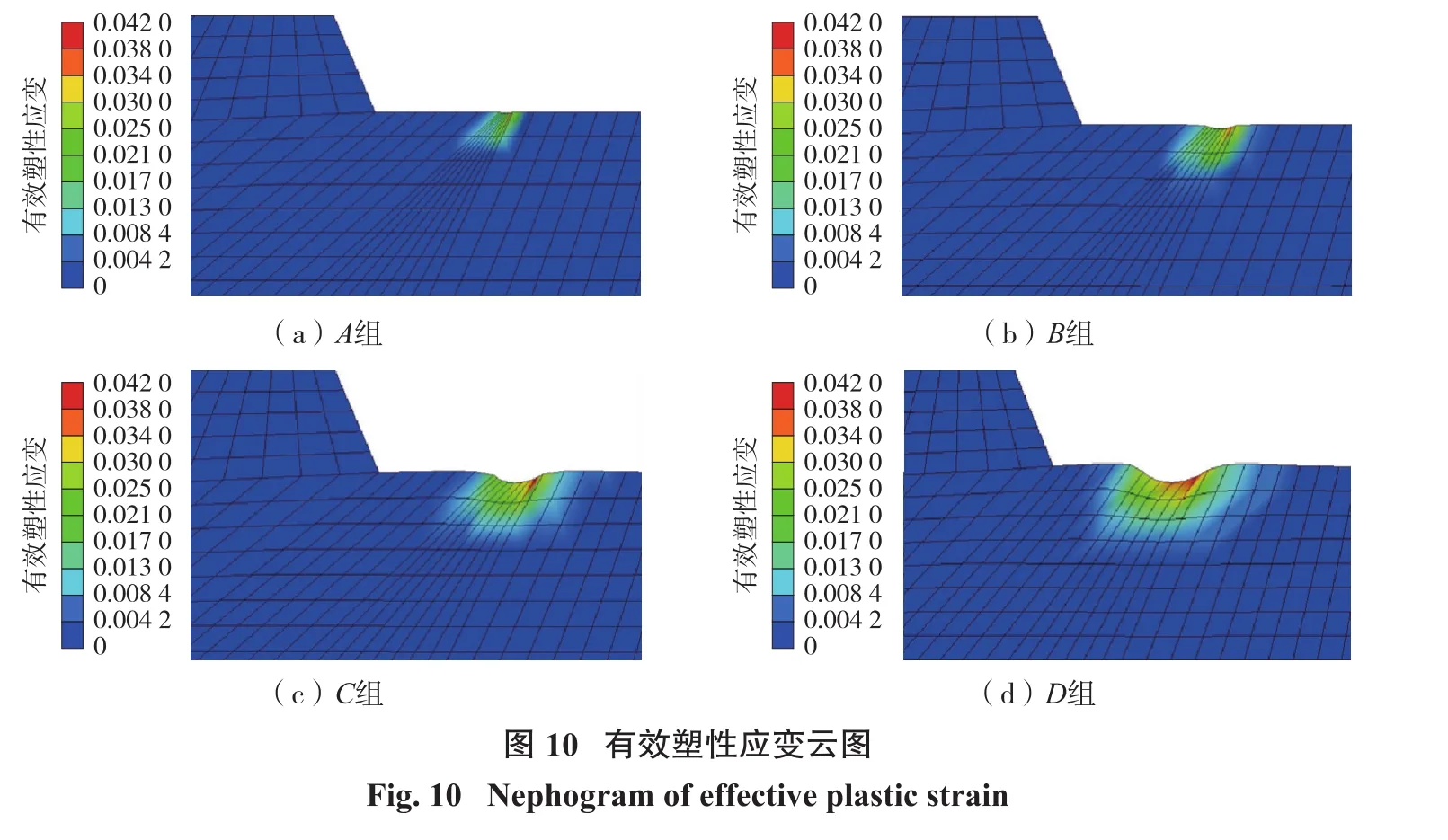
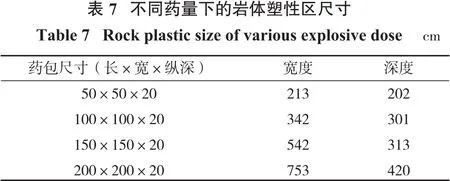
塑性區范圍對應于實際生產中的爆破漏斗，由于上部為自由面，爆破漏斗呈現出的水平尺寸大于豎直尺寸的特征。隨著裝藥量增加，水平方向塑性區增幅遠大于豎直方向。根據網格變形幅度也可以看出，后兩組模型呈現出明顯的“凹坑”，且“凹坑”兩側受到擠壓有輕微凸起，說明起爆藥量控制著爆源附近的巖石破碎范圍。4組模型監測同一位置單元的位移—時程曲線如圖11所示。

由圖11可知：單元變形發生在初始應力作用的基礎上，當爆破應力波傳至單元后，單元迅速產生較大形變，曲線第1個上升階段對應爆破動力主導下的變形階段。由于巖石材料是彈塑性材料，上述單元變形量大部分超過彈性形變的極值，呈現出一定的塑性變化。而大藥量爆破動力加載過后的單元位移維持在一個特定水平發生波動，這一階段的變形是衰減后的爆破動力與地應力共同作用的結果。對于藥量最小的A組模型，距離爆源較遠單元的初始動力響應表現為小范圍變形，隨后變形量才產生大幅度波動，說明小藥量藥包對遠處單元影響較小，主要是提供擾動后作用。

不同藥量方案單元位移結果如圖12所示。由圖12可知：隨著監測單元與藥包距離增加，位移呈減小趨勢。起爆藥量越大，該趨勢愈加明顯，說明單元位移受藥量影響較大，這與上述分析一致。同一單元的位移也會隨著起爆藥量增加而增加。當爆心距持續增加，不同藥量方案的單元位移差距越來越小。因此，單次起爆藥量是影響邊坡穩定性的主要因素之一，最佳的起爆藥量不僅能保證起爆時的邊坡穩定性，又能確保礦山采剝生產高效進行。藥包破碎范圍主要為藥包下方半圓形區域，距離坡底25 m。隨著起爆藥量增加，藥包近區單元位移不斷上升。藥包截面尺寸為150 cm×150 cm時（藥量562.5 kg），爆源近區單元位移約為藥包截面尺寸為200 cm×200 cm（藥量1 000 kg）下的1 /2。藥包藥量增大則破碎范圍增大，隨之而來的爆震危害也更明顯。藥量過大也會造成爆源附近的碎石飛散，不利于裝運。

為減輕爆震危害，應當盡可能維持最優藥量爆破，且炸藥選型應選取爆速較低、威力較小的炸藥。當炸藥量較大時，盡可能分散布置到多個炮孔中，采用分段微差起爆方式。爆破作業時，應注意邊坡上部滾落碎石。當起爆點附近有重要構筑物時可采用預裂爆破形成預裂縫，削弱爆破振動對構筑物的影響。

4 結 論

本研究運用AUTO CAD與ANSYS聯合建模技術建立高陡邊坡動靜耦合分析數值模型，采用ANSYS靜力隱式計算方法得到邊坡剝離后的地應力分布規律，將其導入LS-DYNA軟件中進行顯式動力分析，有效還原了地應力遷移環境下的爆震傳播效果，實現了顯式—隱式轉換下的高陡邊坡動靜力學耦合分析，得出如下結論：

（1）動靜耦合的計算模式有效還原了高陡邊坡的初始應力，上覆巖層剝離后邊坡體坡面及臺階位置發生卸荷力學行為，單元變形產生小范圍回彈，使爆破應力波作用均在應力重分布的基礎上開始響應。在這一計算模式下，邊坡面成為了應力波傳播的自由震蕩空間，當振動速度超過其臨界值時即發生破壞，實際生產中坡頂易發生碎石滾落，需重點防范。

（2）對顯式—隱式聯合計算結果進行塑性變化分析發現，炸藥量越大，塑性范圍隨之呈正比增長關系；爆心距較小的單元動力響應過程始于爆破引發的大變形加載階段，隨后在爆破動力與地應力耦合作用下持續震蕩直至平穩。通過對不同起爆藥量下的質點振動速度及單元位移分析，確定藥包尺寸為150 cm×150 cm×20 cm為安全高效生產的最優裝藥參數。

（3）根據不同藥量爆破動力強度分析，提出了減震降災措施：當炸藥量較大時，盡可能分散到多個炮孔中，采用分段微差起爆方式；有爆破生產時，應注意邊坡上部滾落碎石。當起爆點附近有重要構筑物時可采用預裂爆破形成預裂縫，削弱爆破振動對構筑物的影響。顯隱轉換分析方法有效實現了地應力影響下的爆震傳播規律研究，但分析中對邊坡坡體內的不良地質體考慮有限，在今后研究中通過融合節理的精細化建模方法，能夠更好地實現仿真效果。