風廓線雷達數據誤差分析評估

王大鵬，孫 強，劉 俊，繆明榕，周紅根

(1.江蘇省氣象探測中心，南京 210008；2.鹽城市氣象局，鹽城 224001；3.泰州市氣象局，泰州 225300；4.南通市氣象局，南通 226007)

0 引言

風廓線雷達是一種以晴空大氣為主要探測對象的遙感設備，其作用原理是利用大氣湍流對電磁波的散射作用，提供以風場為主的多種數據產品。根據多普勒效應可以獲取不同波束方向的徑向速度。在一定風場條件下，利用處在同一高度面上幾個點的徑向速度計算水平風。風廓線雷達的探測方式為連續的無人值守的定點遙感方式，其觀測資料具有很高的時間和空間分辨率。時間分辨率一般為6 min，空間高度分辨率一般為幾十米到一百米左右，這是其他探測手段很難達到的高時空分辨率。這種探測優勢和資料特點為日常監測預警預報以及數值模式預報帶來了極大方便；因此，風廓線雷達風場數據的質量是氣象部門十分關心的問題。隨著風廓線雷達布網的不斷深入，如何使用風廓線雷達的數據也成為急需解決的問題。

中國風廓線雷達網的建設實現了高時空分辨率風廓線雷達數據的實時獲取。吳志根[1-3]、翟亮[4-6]等開展邊界層風廓線雷達與二次雷達測風數據的對比分析研究；鄧闖[7，8]呂博[9，10]等評估了風廓線雷達的測風準確度。文章利用南京站風廓線雷達與探空站同址，對每日4次的探空觀測數據與風廓線雷達風場數據進行直接對比檢驗，分別利用探空觀測數據和模式再分析的風場數據與其進行對比分析，實現對南京風廓線雷達的數據質量的系統定量評估。

1 風廓線與L波段探空觀測數據對比檢驗

南京站(58238)風廓線雷達與探空站在地理位置上重合，因此可將探空觀測數據與風場數據進行直接對比檢驗。探空觀測的原理是利用測風雷達跟蹤自由上升氣球，根據一段時間內氣球飄移的距離計算水平風，每次觀測需要60～70 min，每組數據是取樣時間點前后幾分鐘的平均值。在用無線電探空儀測風時，因為氣球的平飄，獲取的廓線并不是嚴格的局地垂直廓線。從嚴格意義上來說，由于風廓線雷達風場和探空風場的觀測方式不同，兩者在比較時，是建立在時間和空間近似一致的假設之上的。

1.1 風廓線雷達風場誤差的統計檢驗

風廓線雷達所提供的水平風場產品，有6 min資料、0.5 h和1 h的平均資料。為了分析和檢驗這3種資料的準確度，將南京站的L波段秒級探空資料分別與這3種形式的風廓線雷達資料進行匹配和比較，選取時段為2014年，每天4個時次。

首先，取6 min資料進行對比檢驗。以南京站探空風速作為參考值，從2014年的風速誤差散點分布可以看出，25，422個樣本中，風速平均偏差為-0.35 m/s，均方根誤差為1.60 m/s，相關系數0.91。若定義風速誤差小于3 m/s時為有效數據，則風廓線風速資料的數據獲取率為86.08%(有效數據樣本占總體數據樣本的百分比)。從風向誤差的散點分布可以看出，在25，422個樣本中可以看出，風向的平均偏差為4.53°，均方根誤差為17.99°，相關系數0.96。若定義風向誤差小于20°時為有效數據，則風廓線風向資料的數據獲取率為74.64%。從風廓線6 min風場資料和探空觀測數據的整體對比來看，風速基本無偏差且誤差較小，但個別時次的樣本存在風廓線風速偏大的情況。此外，當風速較大時，風廓線資料風速值相比探空觀測數據偏小；對于風向誤差，整體偏大，但誤差在合理范圍內。通過風廓線數據與探空資料的匹配數據對的風速和風向偏差的頻率分布，能夠看出風速偏差滿足正態分布。

其次，取0.5 h平均資料進行對比檢驗。通過分析2014年的風速誤差散點分布可以得出25，729個樣本中，風速平均偏差為0.31 m/s，均方根誤差為1.59 m/s，相關系數0.91，風速的數據獲取率為86.02%。從風向誤差的散點分布可以得出，風向的平均偏差為6.02°，均方根誤差為18.30°，相關系數0.96，風向的數據獲取率為74.20%。從風廓線0.5 h的平均風場資料和探空觀測數據的對比分析來看，風速基本無偏差且誤差較小；風向偏差較大，但誤差在合理的范圍之內。

最后，取1 h平均資料進行對比檢驗。圖1(a)給出了2014年的風速對比散點分布。25，972個樣本中，風速平均偏差為0.39 m/s，均方根誤差為1.52 m/s，相關系數為0.92，風速的數據獲取率為87.25%。圖1(b)給出了風向誤差的散點分布，風向的平均偏差為5.41°，均方根誤差為16.93°，相關系數0.96，風向的數據獲取率為76.47%。從風廓線1 h平均的風場資料和探空觀測數據的對比分析來看，其大致的誤差特征與瞬時資料和0.5 h平均資料類似，不過值得注意的是，在風速誤差方面，1 h平均資料中并無風速值異常偏大的樣本(圖1a)；在風向誤差方面，其統計特征與瞬時資料較為相似(圖1c，d)。

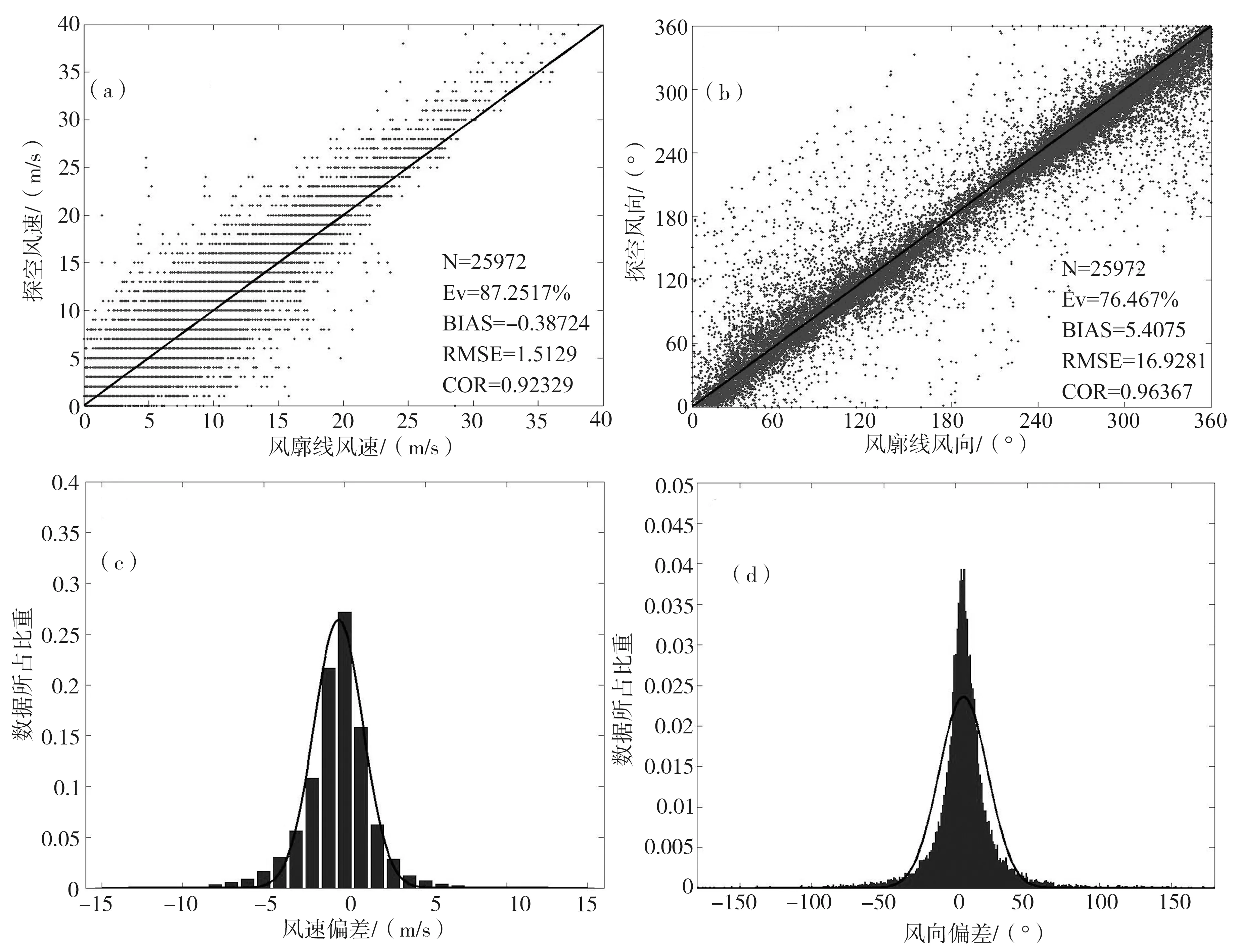
圖1 2014年1 h平均風廓線資料與探空觀測的匹配數據對的散點分布和要素偏差的頻率分布：(a)風速誤差散點分布；(b)風向誤差散點分布；(c)風速偏差頻率分布；(d)風向偏差頻率分布

1.2 風廓線風場資料誤差的分布特征

為了深入分析風廓線風場資料的誤差分布特征，以1 h平均的風廓線資料為例，給出了其2014年的風場誤差隨高度變化的統計特征。在低層，風速均方根誤差接近2 m/s，風向均方根誤差超過20°；隨著高度增加，風速和風向的均方根誤差減小，風速誤差穩定在1.5 m/s左右，風向誤差大約為17°，當超過3000～4000 m高度時，風速均方根誤差略有增大，風向均方根誤差略有減小，整體而言，風速和風向的均方根誤差隨高度變化不大。對于偏差特征，在低層，風廓線風速偏大，當隨高度增加時，整體上風速偏小；而風向一直存在微小的正偏差[11]。

圖2給出風廓線資料風速及風向的均方根誤差隨風速觀測值自身大小的變化。從圖中可以看出，與探空觀測相比，風速測量的均方根誤差隨風速測量值增長；同時，風向的均方根誤差隨風速值顯著下降。由于高空風速較大，相比低層，其風速均方根誤差較大，風向均方根誤差較小。

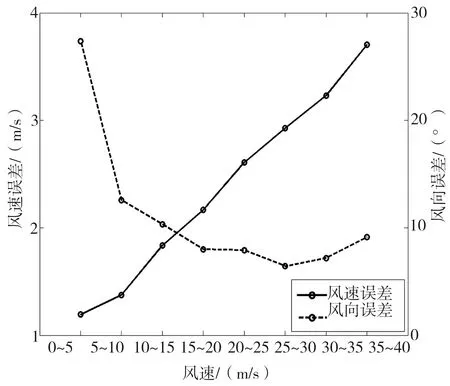
圖2 風速及風向的均方根誤差隨風速的變化

為進一步揭示風廓線風場資料隨時間的變化特征，文章分別計算每個月的風場偏差和均方根誤差，并統計其變化。得出結論，從單一的南京站風廓線雷達分析來看，無論風速還是風向，其誤差隨時間的變化均不明顯，即不存在明顯的季節變化特征。

2 風廓線與FNL再分析數據的對比檢驗

借助NCEP全球模式的FNL再分析數據對南京風廓線雷達的風場資料進行對比檢驗。為了使風廓線雷達與1°×1°再分析資料的匹配數據對在空間上具有一致性，在經度、緯度和海拔高度3 個方向上分別對FNL再分析資料做插值處理，將其投影到風廓線雷達數據的坐標位置，從而進行直接對比。

利用2014年全年的FNL數據和風廓線數據建立匹配數據對，以FNL再分析資料作為參考值，統計風廓線資料的風場誤差。表1和表2給出了南京雷達2014年全年的統計誤差。為了更細致地分析風廓線數據質量，統計分析包括了6 min、0.5 h平均和1 h平均3種資料。3種資料的風速和風向的統計誤差都十分接近，這與探空觀測數據的對比分析結果相似。從風速誤差(表1)來看，風速均方根誤差大約為1.98 m/s，誤差較小，且相關系數較高，表明南京站風廓線的風速資料可信。對于風向誤差(表2)，南京站均方根誤差大約在23°左右，其偏差約為6°。

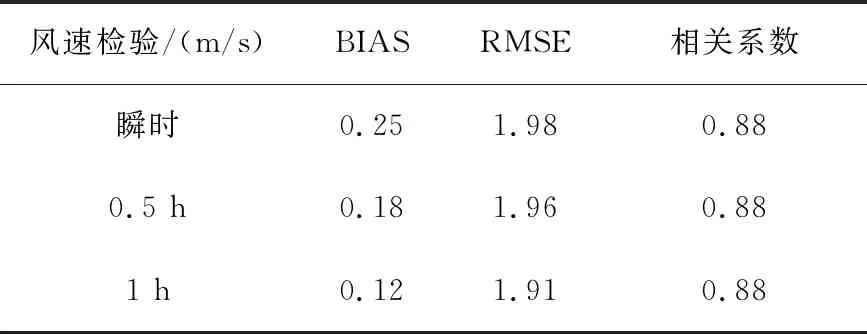
表1 2014年南京風廓線雷達的風速誤差統計

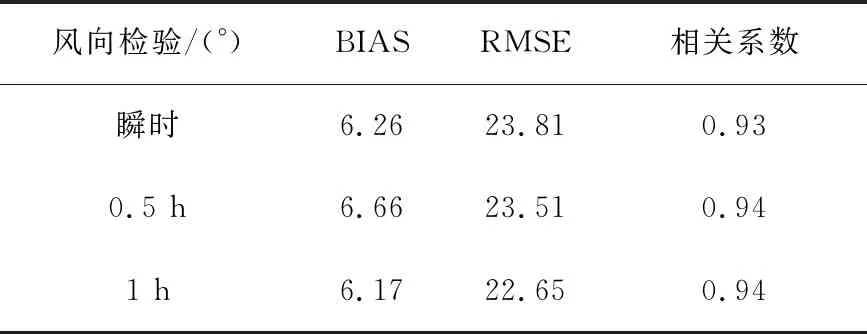
表2 2014年南京風廓線雷達的風向誤差統計

文章分析了南京站風廓線的風場誤差隨高度的變化特征。采用FNL再分析數據作為真值與采用探空觀測數據作為真值的對比結果類似，風速呈現出低層正偏差、高層負偏差的特征，均方根誤差低層較小，高層較大；風向隨高度變化呈現出一致的正偏差，但偏差不明顯；同時，也分析了南京站風廓線風速和風向誤差的逐月變化。與采用探空觀測數據作為真值的對比結果類似，無論風速還是風向，其誤差隨時間的變化不明顯，不存在明顯的季節變化特征。

以FNL再分析資料的風場數據作為真值對2014年南京風廓線雷達的風場數據進行檢驗評估，風速誤差約1.9 m/s，風向誤差23°。從誤差分布特征來看，與探空觀測數據進行對比所得到的結論一致。

3 結束語

文章詳細分析了2014年的南京站風廓線資料與探空觀測數據的對比誤差特征，分別利用探空觀測數據和模式再分析的風場數據與其進行對比分析，實現了對南京風廓線雷達的數據質量的系統定量評估。

利用探空觀測數據進行對比，對于6 min資料、0.5 h平均資料和1 h平均資料3種風廓線風場產品，其風速和風向的誤差統計結果較為相似。風速偏差約-0.3 m/s，均方根誤差約1.5 m/s；風向偏差約5°，均方根誤差約17°。相比之下，6 min資料存在個別樣本風速偏大的情況，而經過時間平均后，1 h平均資料不存在風速奇異值的問題。從風場誤差的垂直分布看，在低層，由于風速較小，所以風速誤差較小，但風向誤差較大；而在高層，由于風速較大，風速誤差整體較大，風向誤差較小。從風場誤差的時間變化來看，不存在明顯的季節特征，風廓線資料誤差的逐月變化較小。

以FNL再分析資料的風場數據作為真值對2014年南京站風廓線雷達的風場數據進行檢驗評估，南京站風廓線風速誤差約1.9 m/s，風向誤差23°。從誤差分布特征來看，與探空觀測數據進行對比所得到的結論一致。