《鐘面角——已知角度求時間》學(xué)思案與教學(xué)反思

陳鈺玨

學(xué)習(xí)主題

《鐘面角——已知角度求時間》

學(xué)習(xí)目標(biāo)

了解時針、分針的轉(zhuǎn)速，認(rèn)識鐘面角;

掌握運用角的和差來解決鐘面角問題;

3、在實例的分析、思考、總結(jié)中，感悟解決鐘面角問題的一般方法。

學(xué)習(xí)過程

【問題1】

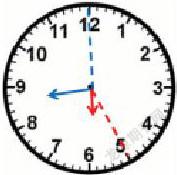
已知：趙老師是早上五點半到六點之間起床的，當(dāng)時表上時針和分針的夾角為90°。

請問：趙老師是幾點起床的？

思考：

時針的速度：_____°/分;分針的速度：_____°/分;

（2）作出大致圖象，圖中有哪些已知角度的角？

設(shè)趙老師是五點x分起床的，時針轉(zhuǎn)過的角度是_______度，分針轉(zhuǎn)過的角度是______度;

（3）圖中這幾個角之間可以找到怎樣的等量關(guān)系？________________________

（4）在解決這個問題時的步驟？

【問題2】

已知：趙老師在早上六點多到學(xué)校，當(dāng)時表上時針和分針剛好重合。

請問：趙老師是幾點到校的？

思考：

作出圖象，找出已知角度的角;

設(shè)趙老師是六點x分到校的，時針轉(zhuǎn)過的角度是_______度，分針轉(zhuǎn)過的角度是______度;

（3）可找到的數(shù)量關(guān)系：______________________

【問題3】

已知：趙老師在早上八點多與家長進(jìn)行了交流。開始交流時表上時針和分針成120°角，交流結(jié)束時，時針和分針成60°角，且交流時間不超過一小時。

請問：趙老師與家長交流了多少時間？

思考：

作出圖像，找到時針和分針的起始位置及終止位置;

（提醒：在這里，時針和分針的終止位置會出現(xiàn)幾種情況？）

找出已知角度的角、時針、分針轉(zhuǎn)過的角度;

找出數(shù)量關(guān)系，列出方程。

【小結(jié)】

1、時針、分針的速度________________________

2、已知角度求時間的關(guān)鍵點：

3、涉及到哪些數(shù)學(xué)思想？

問題參考

問題1：

（把五點看成時時針和分針的起始位置，此時它們的夾角為150°;把趙老師起床時間看成是時針和分針的終止位置，此時它們的夾角是90°）

（3）6x-0.5x=90+150

（4）①找出時針、分針的起始位置、終止位置;

②找出已知角度的角，時針、分針轉(zhuǎn)過的角度;

③根據(jù)角度之間的數(shù)量關(guān)系列方程

問題2：

（1）

起始位置六點時時針和分針的夾角180°;終止位置時針和分針重合時夾角為0°

（2）0.5x;6x

（3）6x-0.5x=180

進(jìn)一步明確解題步驟：

①找出時針、分針的起始位置、終止位置;

②找出已知角度的角，時針、分針轉(zhuǎn)過的角度;

③根據(jù)角度之間的數(shù)量關(guān)系列方程。

問題3：

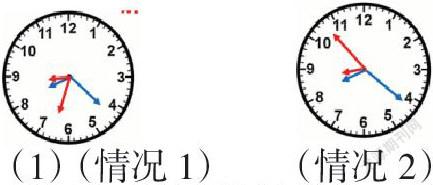
（1）（情況1）? ? ? （情況2）

（注意：通過實際操作，可以發(fā)現(xiàn)在該問題背景下，時針和分針的終止位置會出現(xiàn)兩種情況，因此需要分類討論））

（2）設(shè)趙老師與家長交流了x分鐘，

已知角度的角：起始位置角度：120°;終止位置角度：60°

時針轉(zhuǎn)過的角度：（0.5x）°;分針轉(zhuǎn)過的角度：（6x）°

（3）情況1：6x-0.5x=120-60

情況2：6x-0.5x=120+60

（注意：在解決此類問題時，需結(jié)合圖形，分類討論。）

小結(jié)

1、時針的轉(zhuǎn)速0.5°/分，分針的轉(zhuǎn)速6°/分

2、①找出時針、分針的起始位置、終止位置;

②找出已知角度的角，時針、分針轉(zhuǎn)過的角度;

根據(jù)角度之間的數(shù)量關(guān)系列方程。

3、方程思想、分類討論思想、數(shù)形結(jié)合思想

反思與評價

數(shù)學(xué)與生活實際有著密切的聯(lián)系，哪里有生活，哪里就有數(shù)學(xué)，生活中處處洋溢著數(shù)學(xué)的氣息。如果離開了生活單純地去探討數(shù)學(xué)那肯定是枯燥、乏味的，學(xué)生也只是被動的去接受知識，那與現(xiàn)在的課程改革也是相背而行的。因此在本節(jié)課的設(shè)置中，用一段關(guān)于趙老師現(xiàn)實生活的采訪，串聯(lián)四個問題，以實際問題為切入點引入主題，讓學(xué)生體會到數(shù)學(xué)就在身邊，增加課堂的趣味性。

問題1中，學(xué)生通過動手操作，可以找出題目背景下的90°角，并作出相應(yīng)圖象，在此告知學(xué)生把這個時刻的時針分針的夾角看成是它們的終止位置，那么可以找出它們的起始位置嗎？有學(xué)生提出可以把五點三十分看成起始位置，此時提問“能馬上說出五點三十分時時針分針的夾角嗎？”，從而讓學(xué)生發(fā)現(xiàn)把五點三十分作為起始位置并不合適，從而來尋找更合適的起始位置。所以把五點時時針分針的位置看成起始位置，并且說出起始位置的夾角。在解決了問題1后，讓學(xué)生根據(jù)解題過程來概括解題步驟，這里充分發(fā)揮學(xué)生主體意識，培養(yǎng)學(xué)生語言概括能力。

問題2是在問題1的基礎(chǔ)上，知識現(xiàn)用。由于學(xué)生對于該類題型解題還不夠熟練，所以需要給予一定的耐心，同時作出適當(dāng)?shù)囊龑?dǎo)。這里要注意時針、分針的終止位置夾角為0°。

問題3是在前兩個問題的基礎(chǔ)上，又加入分類討論的過程。經(jīng)過前兩個問題的訓(xùn)練，學(xué)生已基本掌握解題步驟，可以較快地找到所需角從而列出方程來而求解。但絕大部分學(xué)生在求解過程中只考慮了一種情況，所以在實際教學(xué)中，我分別展示了考慮了不同情況的兩個學(xué)生的答案，學(xué)生看完就會恍然大悟，意識到在此需要分類討論。對于這個問題中的兩種情況，很多學(xué)生不是不會做，而是缺乏解題經(jīng)驗，思維局限，這就需要教師的多引導(dǎo)與提醒，注重積累。

實際教學(xué)中教師必須要注意引導(dǎo)學(xué)生認(rèn)識到數(shù)學(xué)理論和生活實際的相互作用 ，然后聯(lián)系學(xué)習(xí)目標(biāo)結(jié)合學(xué)生的生活經(jīng)驗以及認(rèn)知規(guī)律 ，努力創(chuàng)設(shè)豐富多彩 、生動活潑、富有生活氣息的教學(xué)情境和練習(xí)實踐活動，讓學(xué)生掌握從數(shù)學(xué)的角度觀察事物、發(fā)現(xiàn)問題 ，并且能解決問題。