基于線性規劃的房地產開發業態優化

周 洪

(四川省濱水城鄉發展有限責任公司，四川 成都 610000)

在房地產開發過程中，經常涉及在滿足容積率要求的情況下，多種業態，如商業、別墅、花園洋房和高層住房等在業態上的分配問題。一般情況下，基于行業經驗，能夠得到一個相對理想的分配方案，但通常這種分配是基于行業經驗，在某些情況下可能不是滿足目標的最優方案。筆者設想將這個問題抽象為一個線性規劃模型。在一定的目標要求情況下，把容積率、總面積要求等抽象為約束條件，通過求解線性規劃模型得到使得目標函數最優的各類建筑的最優建筑面積。

1 研究樣地的選擇及初始業態規劃

文中選取了某縣級城市新城區25.27hm2土地，打造以別墅、花園洋房、小高層為主的高端生態居住區。其中要求商業比例不超過10%，容積率不超過1.5。按照某知名規劃設計院對本項目的概念設計方案，項目計容總建筑面積約37.92萬m2，商業建筑面積約36 500m2，約9.6%。住宅建筑面積約34.27萬m2，約90.4%，其中別墅：48 878m2、花園洋房72 400m2、小高層：160 760m2。

根據市場調研分析，各業態的市場售價為：商業1.8萬元/m2，別墅1.0萬元/m2，花園洋房0.6萬元/m2，小高層0.45萬元/m2。則項目初始總收益為：

R初始=36 500×1.8+48 878×1.0+72 400×0.6+160 760×0.45=230 360萬元

2 問題描述及線性規劃模型

現有一塊面積為S的土地，要在這塊土地上規劃商業、別墅、花園洋房和高層住房4種建筑。商業面積占總建筑面積的最大百分比為λ，即商業面積不超過總建筑面積的百分比為λ。每種建筑有自己的單價和容積率要求，在滿足容積率和總土地面積的情況下，如何規劃這4種建筑的面積數使得總利潤最大。各個參數的含義描述，如表1所示。

根據以上假設，所建立的線性模型如下：

R=max(c1x1+c2x2+c3x3+c4x4)

(1)

(2)

x1+x2+x3+x4≤αS

(3)

x1≤λ×αS

(4)

x1≥0,x2≥0,x3≥0,x4≥0

(5)

(1)式為目標函數，最大化開發商的收益；(2)式為對各類建筑占用總土地面積的約束，即各類建筑的占用的總土地面積不得超過規劃的總的土地面積；(3)式為對各類建筑的總建筑面積的約束，即各類建筑的總建筑面積不得超過滿足容積率要求下的最大的建筑面積；(4)式為對商業面積的限制，即整個規劃中，要求商業面積不超過總建筑面積的百分比。

3 算例

根據以上建立的模型和選擇的研究樣地，各參數的取值如表1和表2所示。

表2 單位建筑面積售價和容積率參數要求

表3 這塊土地的總面積及總容積率要求參數

商業面積占總建筑面積的最大百分比為λ=10%，目標函數及約束條件如公式(6)～(10)所示。

R=max(1.8x1+1.0x2+0.6x3+0.45x4)

(6)

(7)

x1+x2+x3+x4≤380 100

(8)

x1≤38 010

(9)

x1≥0,x2≥0,x3≥0,x4≥0

(10)

將以上參數代入模型，應用專業的求解整數規劃的ILOGOPL編程語言編程進行求解，得到的最優解及最大收益如表4所示。

表4 最優解及最大收益 單位：m2

即，商業的建筑面積為38 010m2，別墅建筑面積為0，花園洋房的建筑面積為24 760m2，高層住房的建筑面積為95 020m2。

項目可實現的總收益：R最優=259 420萬元。該最優收益比初始總收益高出29 060萬元。

4 單位售價的敏感性分析

4.1 商業部分單位售價變化對最優解的敏感性

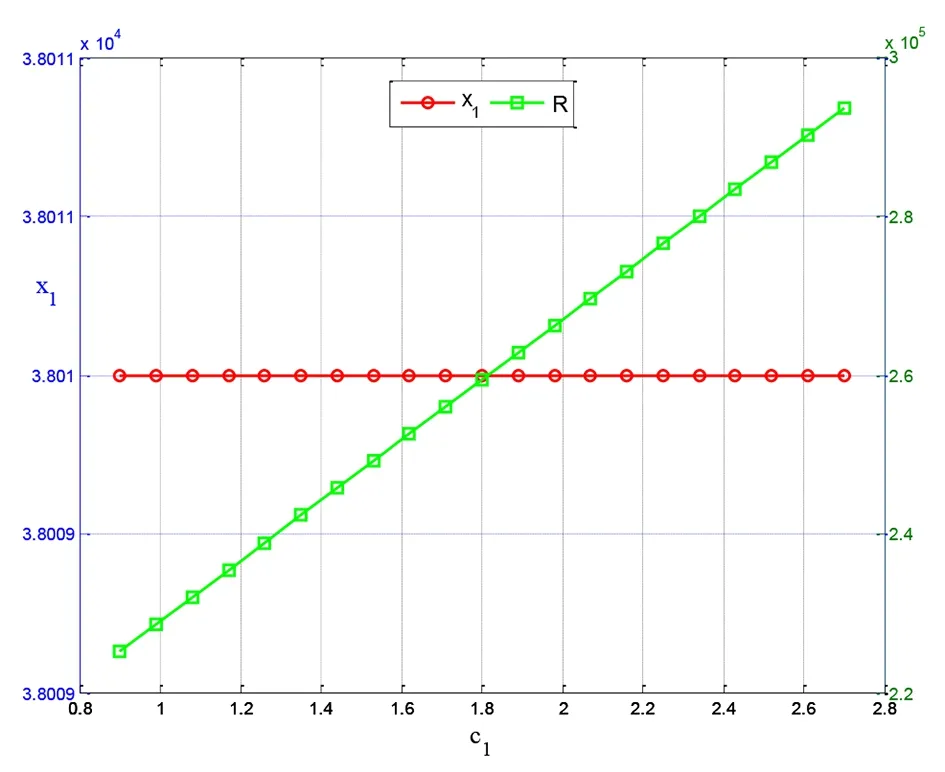
圖1 商業部分單位售價變化對最優解的敏感性

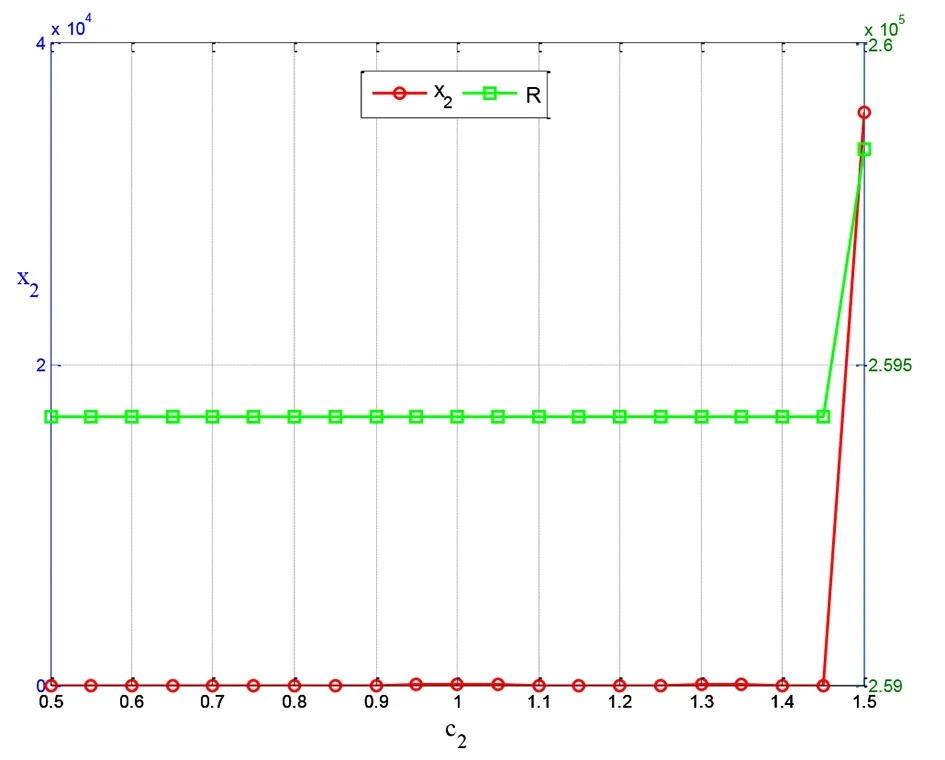
圖2 別墅部分單位售價變化對最優解的敏感性

從圖1可以看出，商業部分單位售價在-50%～50%(0.9萬元～2.7萬元)之間波動時，最優解不發生變化。

4.2 別墅部分單位售價變化對最優解的敏感性

從圖2可以看出，別墅部分單位售價在-50%～50%(0.5萬元～1.5萬元)之間波動時，其中，在0.5萬元≤別墅售價≤1.45萬元時，最優解不發生變化，當1.45萬元≤別墅售價≤1.5萬元時，最優解發生顯著變化，別墅面積持續提高。

4.3 花園洋房部分單位售價變化對最優解的敏感性

圖3 花園洋房部分單位售價變化對最優解的敏感性

從圖3可以看出，花園洋房部分單位售價在-50%～50%(0.3萬元～0.9萬元)之間波動時，其中，當0.3萬元≤花園洋房售價≤0.51萬元時，最優解不發生變化，此時花園洋房最優面積為0；當0.51萬元≤花園洋房售價≤0.52萬元時，最優解發生變化，此時花園洋房持續增加；當0.52萬元≤花園洋房售價≤0.81萬元時，最優解不發生變化；當0.81萬元≤花園洋房售價≤0.84萬元時，此時最優解發生變化，花園洋房面積在原有基礎上持續提高，當0.84萬元≤花園洋房售價≤0.9萬元時，此時花園洋房面積在新的位置上保持平衡。

4.4 高層部分單位售價變化對最優解的敏感性

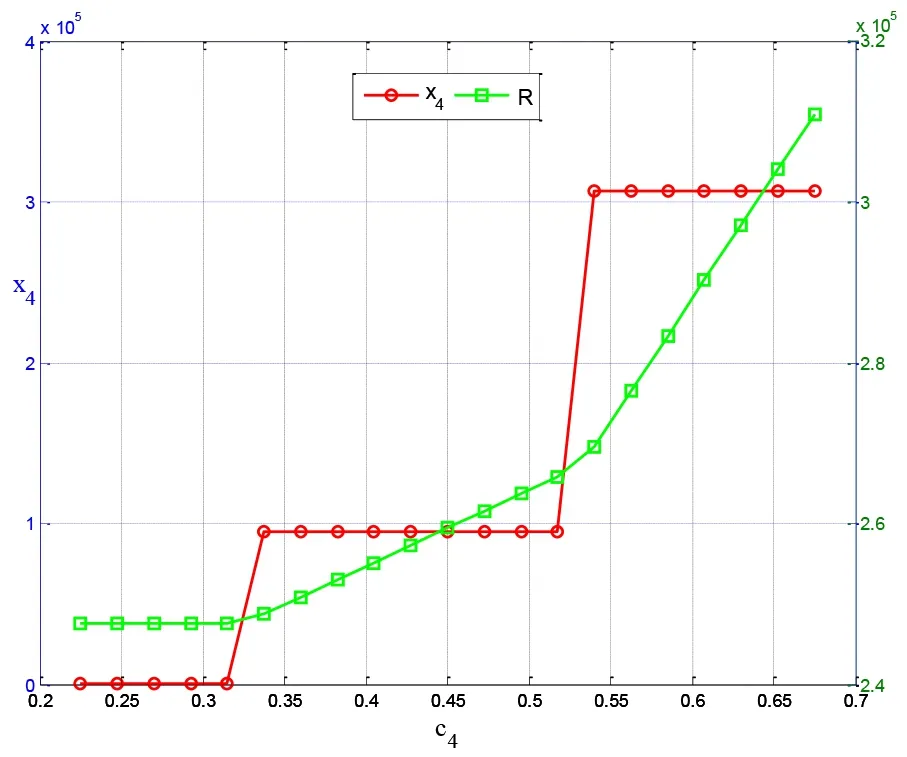
圖4 高層部分單位售價變化對最優解的敏感性

從圖4可以看出，高層部分單位售價在-50%～50%(0.225萬元～0.675萬元)之間波動時，其中，當0.225萬元≤高層售價≤0.32萬元時，最優解發生變化，高層面積為0，當0.32萬元≤高層售價≤0.34萬元時，此時最優解發生變化，高層面積在原有基礎上持續提高，當0.34萬元≤高層售價≤0.52萬元時，此時最優解不發生變化。當0.52萬元≤高層售價≤0.54萬元時，此時最優解發生變化，高層面積在原有基礎上面積持續提高。當0.54萬元≤高層售價≤0.675萬元時，此時高層面積在提高后保持新的平衡。

5 結束語

用定量的思想，將房地產開發中的業態的配比問題抽象成線性規劃模型，并用專業的求解線性規劃軟件IBM ILOG CPLEX12.51，用ILOG OPL編程語言編程進行求解，得到了最優的分配方案。這種應用優化模型來實現最優化的房地產開發方案的思想可以在房地產開發過程中得到很好的應用。在模型的復雜度不高的情況下，IBM ILOG CPLEX12.51求解最優解的時間非常短，而且可以得到模型的最優解，而人工經驗值往往不是最優解。正如本文中列舉的案例所述，根據經驗取得初始目標值為R初始=230 360萬元，而利用該模型優化求解后得到的目標值為R最優=259 420萬元。該最優收益比初始總收益高出29 060萬元，實現了商業價值最大化。同時，筆者考慮價格因素變化對最優解的影響，根據價格的變化方向分析出最優解的變化趨勢。