基于擴(kuò)展卡爾曼濾波的三軸氣浮臺(tái)質(zhì)心位置測(cè)算方法

胡奇飛，李 穩(wěn)

(中聯(lián)恒通機(jī)械有限公司，湖南 長(zhǎng)沙 410073)

0 引言

三軸氣浮臺(tái)通過(guò)氣浮球軸承實(shí)現(xiàn)近似無(wú)摩擦的系統(tǒng)來(lái)模擬太空失重環(huán)境，需要通過(guò)調(diào)平衡裝置將質(zhì)心調(diào)節(jié)到轉(zhuǎn)動(dòng)中心的位置以消除重力帶來(lái)的干擾力矩。因此，調(diào)平衡技術(shù)是實(shí)現(xiàn)高精度氣浮臺(tái)的關(guān)鍵技術(shù)。一般而言，自動(dòng)調(diào)平衡技術(shù)較人工調(diào)平技術(shù)效率高、精度高，是當(dāng)前研究的熱點(diǎn)。

為實(shí)現(xiàn)精確調(diào)平衡，必須先測(cè)算出質(zhì)心的精確位置。通過(guò)Pro/E軟件建立氣浮臺(tái)的三維模型，可以初步計(jì)算氣浮臺(tái)的質(zhì)心位置，但由于電線(xiàn)、焊接點(diǎn)等零部件建模存在困難，這一方法無(wú)法精確計(jì)算出質(zhì)心的位置。起初，研究人員通過(guò)測(cè)量氣浮臺(tái)的擺動(dòng)周期來(lái)測(cè)算質(zhì)心位置的偏移，進(jìn)而進(jìn)行配平。這種方法將氣浮臺(tái)等效為3D復(fù)擺[1]，但這一方法需要反復(fù)測(cè)量氣浮臺(tái)的擺動(dòng)周期，所需調(diào)節(jié)時(shí)間較長(zhǎng)。隨后，人們提出基于氣浮臺(tái)的剛體動(dòng)力學(xué)方程來(lái)控制執(zhí)行機(jī)構(gòu)，調(diào)節(jié)質(zhì)心位置，文獻(xiàn)[2]給出了通過(guò)2個(gè)傾角傳感器實(shí)現(xiàn)水平方向自動(dòng)配平的方法，文獻(xiàn)[3]和文獻(xiàn)[4]提出了在已知轉(zhuǎn)動(dòng)慣量的情況下計(jì)算質(zhì)心的方法。

本文通過(guò)建立三軸氣浮臺(tái)的動(dòng)力學(xué)模型，采用基于最小二乘法和擴(kuò)展卡爾曼濾波處理姿態(tài)信息、計(jì)算質(zhì)心位置，求解配重滑塊位置，實(shí)現(xiàn)氣浮臺(tái)自動(dòng)調(diào)平衡，并與周期反饋算法進(jìn)行比較。

1 三軸氣浮臺(tái)動(dòng)力學(xué)模型建立與數(shù)值仿真

1.1 三軸氣浮臺(tái)全物理仿真設(shè)備

三軸氣浮臺(tái)由支撐座、氣浮球軸承和轉(zhuǎn)動(dòng)臺(tái)體三部分組成。氣浮球軸承通過(guò)球窩上布置的噴嘴噴出高壓氣體，在球窩與球頭間形成一層極薄的氣膜，實(shí)現(xiàn)三軸近似無(wú)摩擦轉(zhuǎn)動(dòng)。氣浮臺(tái)采用傘形結(jié)構(gòu)，其三維模型如圖1所示。

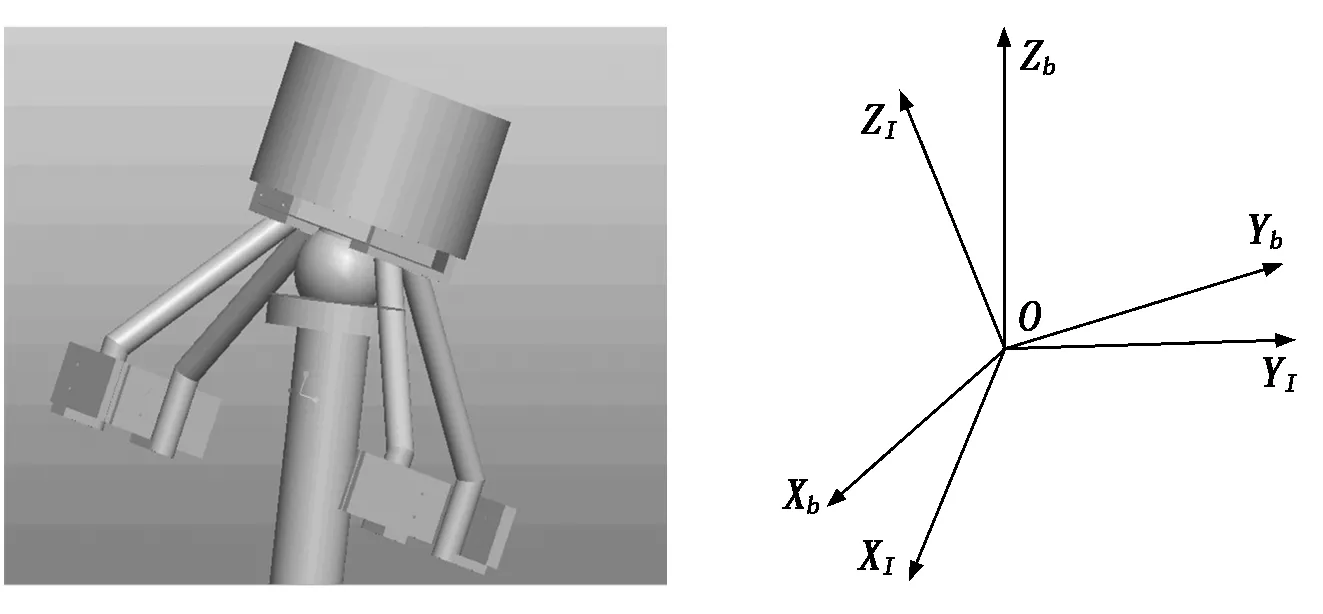
圖1 氣浮臺(tái)三維模型 圖2 慣性坐標(biāo)系和隨體坐標(biāo)系

通過(guò)Pro/E建立的三維模型計(jì)算得到氣浮臺(tái)的質(zhì)量m=136.953 22 kg，其質(zhì)心位置偏移r=[0,0,-1.851 949 3×10-3] m，氣浮臺(tái)相對(duì)于轉(zhuǎn)動(dòng)中心(球頭球心)的轉(zhuǎn)動(dòng)慣量為：

(1)

其中：Ixx、Iyy、Izz分別為氣浮臺(tái)相對(duì)于X、Y、Z的轉(zhuǎn)動(dòng)慣量；Ixy、Ixz、Iyx、Iyz、Izx和Izy均為慣量積。

臺(tái)體上布置一個(gè)兩軸傾角儀，輸出頻率為100 Hz，精度為0.002°，測(cè)量臺(tái)體角度信息，通過(guò)數(shù)據(jù)處理可測(cè)得臺(tái)體的擺動(dòng)周期。

1.2 三軸氣浮臺(tái)動(dòng)力學(xué)模型

以三軸氣浮臺(tái)的轉(zhuǎn)動(dòng)中心作為原點(diǎn)建立隨體坐標(biāo)系O-XbYbZb和慣性坐標(biāo)系O-XIYIZI，如圖2所示。

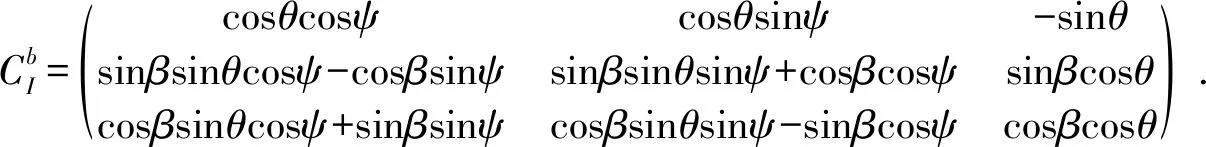
(2)

其中：ψ為偏航角；θ為俯仰角；β為滾轉(zhuǎn)角。

對(duì)于歐拉角速度方程，有：

(3)

又有動(dòng)量矩定理：

(4)

其中：M0為作用于氣浮臺(tái)的外力矩矢量和；L0為氣浮臺(tái)質(zhì)心的動(dòng)量矩。

由于氣浮臺(tái)旋轉(zhuǎn)中心與質(zhì)心不重合，所以又有：

(5)

其中：r為質(zhì)心偏移量；Lc為氣浮臺(tái)相對(duì)于質(zhì)心的角動(dòng)量；ω為氣浮臺(tái)相對(duì)于慣性坐標(biāo)系的角速度。

Lc的計(jì)算公式為：

(6)

將式(5)和式(6)代入式(4),可得：

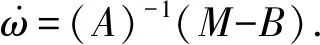
其中：A為角動(dòng)量運(yùn)算矩陣；B為軸向偏移分量；M為重力干擾力矩(這里不考慮重力以外的其他干擾力矩)，其計(jì)算公式為：

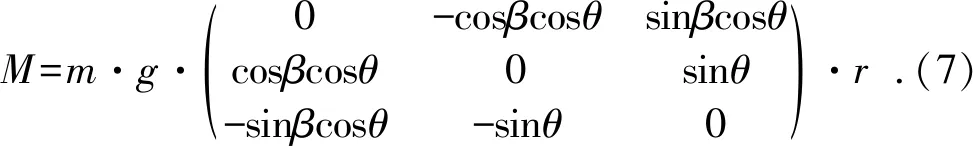
考慮到臺(tái)體轉(zhuǎn)速較慢，ω、r均為小量，只考慮主慣量情況下簡(jiǎn)化得：

(8)

其中：rx、ry、rz分別為質(zhì)心在x、y、z軸的偏移量。

2 基于復(fù)擺模型的質(zhì)心位置測(cè)算方法

當(dāng)氣浮臺(tái)小角度擺動(dòng)時(shí)，可以將臺(tái)體近似作為復(fù)擺處理。將氣浮臺(tái)的運(yùn)動(dòng)分解，假設(shè)只繞X軸運(yùn)動(dòng)，復(fù)擺周期為：

(9)

其中：I為轉(zhuǎn)動(dòng)慣量。

則由式(9)可求解得到質(zhì)心在豎直方向的偏移為：

(10)

水平方向質(zhì)心偏移為：

(11)

其中：α為X軸傾角；χ為臺(tái)體轉(zhuǎn)動(dòng)180°后的傾角。

通過(guò)電機(jī)上移4個(gè)外伸臂的滑塊，氣浮臺(tái)擺動(dòng)周期增大，通過(guò)式(10)換算得出氣浮臺(tái)質(zhì)心，如圖3所示。

圖3(a)可以看出，氣浮臺(tái)擺動(dòng)周期從22 s調(diào)整到160 s耗時(shí)15 min左右，通過(guò)式(10)和式(7)可求得垂直方向質(zhì)心偏移量約為2.78×10-5m，此時(shí)系統(tǒng)干擾力矩約為0.82×10-2Nm。由圖3(b)可以看出，水平方向質(zhì)心偏移量在加大，氣浮臺(tái)平衡性變差。

圖3 周期反饋算法氣浮臺(tái)質(zhì)心調(diào)試效果

3 基于動(dòng)力學(xué)反演的質(zhì)心位置測(cè)算方法

3.1 基于最小二乘法的質(zhì)心位置測(cè)算方法

設(shè)第1個(gè)測(cè)量時(shí)間為t1，第2個(gè)測(cè)量時(shí)間為t2,Δt=t2-t1,基于式(8)，變形可求解質(zhì)心位置：

(12)

將式(12)寫(xiě)為：

ΔΩ=Φr.

(13)

其中：ΔΩ為角速度增量數(shù)組；Φ為3×3矩陣。

則求廣義逆矩陣，質(zhì)心的偏差可通過(guò)最小二乘法求得為：

r=(ΦTΦ)-1ΦTΔΩ.

(14)

通過(guò)最小二乘法，計(jì)算得到質(zhì)心的位置如圖4所示，質(zhì)心測(cè)算速度比周期反饋算法快，但始終存在一定的水平質(zhì)心偏移量。

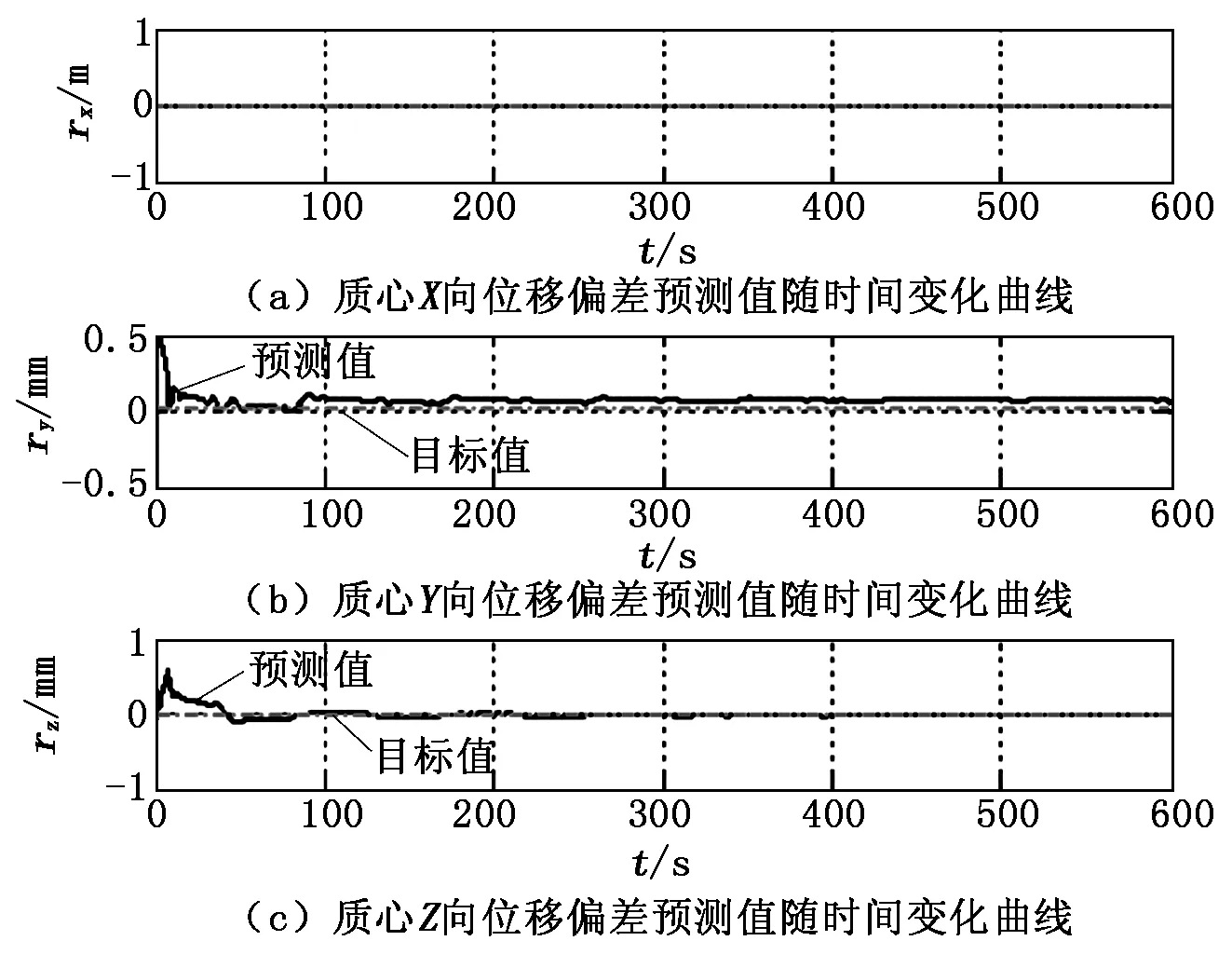
圖4 基于最小二乘法的質(zhì)心位置測(cè)算結(jié)果

3.2 基于擴(kuò)展卡爾曼濾波(EKF)的質(zhì)心位置測(cè)算方法

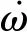
(15)

(16)

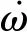
狀態(tài)轉(zhuǎn)移矩陣為:

(17)

(18)

觀測(cè)矩陣為:

(19)

預(yù)測(cè)狀態(tài)的協(xié)方差矩陣Rk與濾波增益矩陣Kk分別為：

(21)

(22)

狀態(tài)值和協(xié)方差矩陣更新為：

(23)

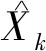
由圖5可知，EKF濾波對(duì)于質(zhì)心位置的測(cè)算收斂速度與最小二乘法相差不大，都優(yōu)于周期反饋算法；但EKF濾波偏差較最小二乘法小，能更精確地測(cè)量質(zhì)心位置。

圖5 基于EKF濾波的質(zhì)心位置測(cè)算結(jié)果

4 實(shí)驗(yàn)結(jié)果與分析

在三軸氣浮臺(tái)上，以氣浮臺(tái)擺動(dòng)周期大于160 s為目標(biāo)，此時(shí)系統(tǒng)的干擾力矩小于10-2N·m，分別采用周期反饋算法、基于最小二乘法的質(zhì)心算法和基于EKF的質(zhì)心算法進(jìn)行調(diào)試。三種算法各取3次調(diào)試結(jié)果，如表1所示。

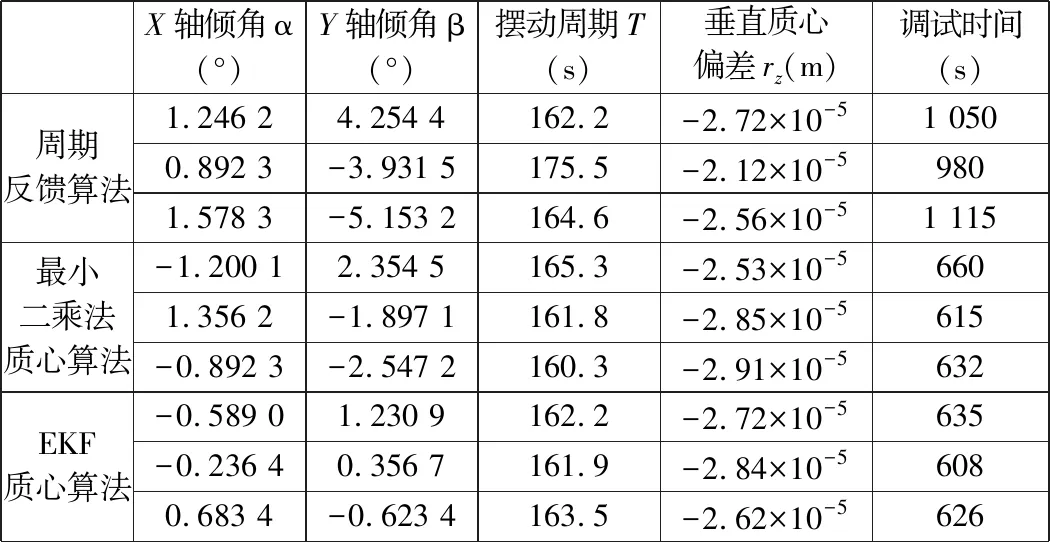
表1 三種不同算法的氣浮臺(tái)周期與質(zhì)心調(diào)試效果對(duì)比

由表1可以看出，氣浮臺(tái)擺動(dòng)周期調(diào)整到160 s，周期反饋算法耗時(shí)最多，需要1 050 s左右；最小二乘法和EKF質(zhì)心算法耗時(shí)相近，為630 s左右；調(diào)整結(jié)束后，Y軸偏擺角度周期反饋算法最大，為4°～5°，EKF算法最小，為1°左右，質(zhì)心位置測(cè)算最精準(zhǔn)。

5 結(jié)論

本文建立三軸氣浮臺(tái)的動(dòng)力學(xué)模型，通過(guò)數(shù)值計(jì)算，仿真其運(yùn)動(dòng)過(guò)程中的角度和角速度變化。其次通過(guò)實(shí)驗(yàn)測(cè)量的角度變化，計(jì)算氣浮臺(tái)的擺動(dòng)周期，從而測(cè)算質(zhì)心的位置。再次，通過(guò)動(dòng)力學(xué)反演的方法，采用最小二乘法和EKF處理姿態(tài)信息，并分析質(zhì)心位置的計(jì)算速度與精度。最后在氣浮臺(tái)上分別采用上述三種算法進(jìn)行調(diào)試，從實(shí)驗(yàn)結(jié)果分析得出，基于EKF算法的調(diào)試時(shí)間最短，質(zhì)心位置精度最高。