研磨子磨耗增粘過程的仿真分析*

張正橋，曾 京

(西南交通大學 牽引動力國家重點實驗室，四川 成都 610031)

0 引言

伴隨著1964年世界上第一條高速鐵路的通車運營，研磨子應運而生，并在隨后的半個多世紀內廣泛應用于高速列車和城軌車輛的制動系統中，起到了良好的輪軌增粘和踏面修型效果[1]。我國也在動車組和城軌列車中大量應用研磨子，通過大量現場及跟蹤試驗數據發現：研磨子可以清除幅值較小的車輪多邊形并持續抑制其發展[2]；另外，研磨子可以減緩踏面等效錐度的增長并起到一定的修型作用，維持較好的車輛橫向穩定性。

鑒于研磨子的材料和作用過程較為復雜，國內的相關研究還停留在表面的試驗現象分析階段。本文以高速列車上配備的研磨子為對象，從基本磨耗機理出發，通過試驗分析和有限元仿真，探討研磨子磨耗增粘過程的變化和性質，明確關鍵工作參數對磨耗過程的影響，以期為研磨子的作用機理研究和作用策略優化提供參考。

1 磨耗原理及過程分析

1.1 粘著磨耗

兩個金屬摩擦副在一定載荷下接觸時表面微凸體相互碰撞并發生塑性變形，接觸面形成粘著結點，當兩固體受力產生相對滑動時微凸體發生剪切斷裂，材料可能脫落成磨屑或遷移到另一方材料表面，這類磨耗叫做粘著磨耗[3]。粘著磨耗初期兩方材料摩擦劇烈，隨著磨耗的進行，材料相互磨合，微粒接觸逐漸緊密，接觸應力減小，磨耗量和磨耗速率逐漸降低[4]。

1.2 磨粒磨耗

硬質磨粒在外加載荷的作用下壓入軟質材料并進行刮擦和切削，從而引發較軟材料機械損耗的過程稱為磨粒磨耗，當比磨耗量(磨耗率與載荷之比)小于10-9mm2/N時發生定常磨耗，即磨耗率隨時間變化基本穩定不變，否則發生嚴重磨耗[5]。磨粒磨耗按照磨粒形狀又分為圓錐磨耗、球形磨耗等，Rabinowicz等[6]首先以圓錐磨粒建立了經典的磨粒磨耗理論模型，如圖1所示，假定單顆圓錐體磨粒半頂角為θ，在載荷P的作用下壓入較軟材料中，壓入深度為h，壓入部分的半徑為r，壓入圓截面面積為A=πr2。

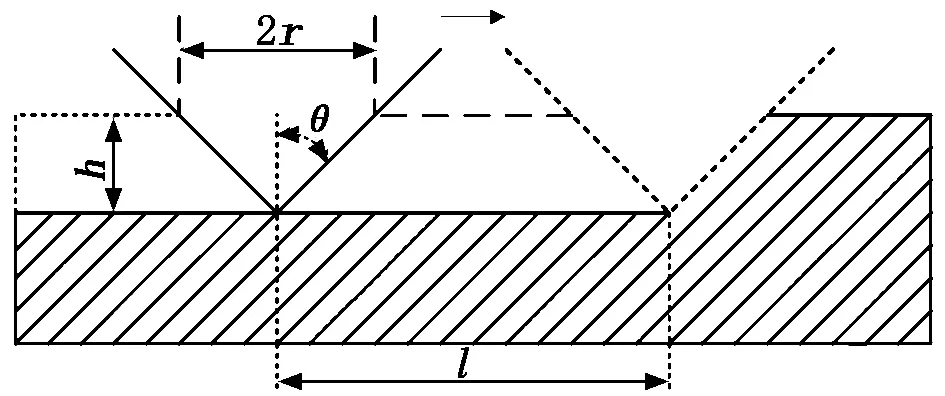
圖1 圓錐磨粒磨耗模型

由布氏硬度的定義可知，被磨金屬材料的硬度H等于載荷P與壓入面積A之比。圓錐形磨粒沿材料表面滑移l形成的溝槽體積即為該單磨粒造成的磨耗體積，通過補形得到該磨耗體為一個三棱柱，體積為：

(1)

整理可得圓錐磨粒磨耗模型磨耗率為：

(2)

同理，建立如圖2所示的球形磨粒磨耗模型。假設球形磨粒壓入深度為h，球體的半徑為R，球體壓入截面半徑為r，總磨耗率可以表示為：

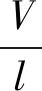
(3)

圖2中灰色直角三角形區域滿足幾何關系：

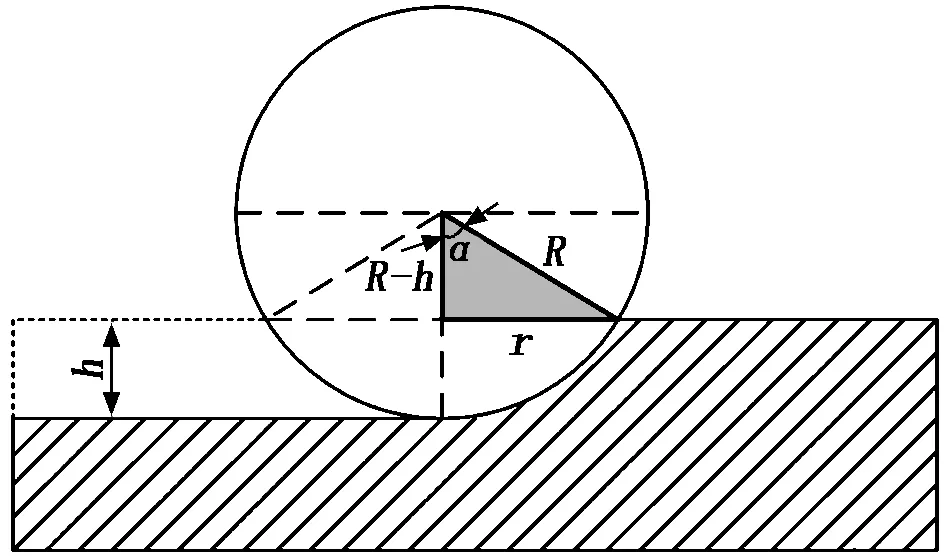
圖2 球形磨粒磨耗模型

(4)

將式(3)和式(4)整理后可得磨耗率為：

(5)

1.3 研磨子與車輪的磨耗試驗

日本鐵道綜合技術研究所[7]利用輪軌高速接觸疲勞試驗臺進行了4組磨耗試驗，試驗工況及目的見表1。試驗③、試驗④中磨耗體積分為研磨子分和除去分，分別代表研磨子造成的踏面磨耗和純輪軌接觸磨耗。

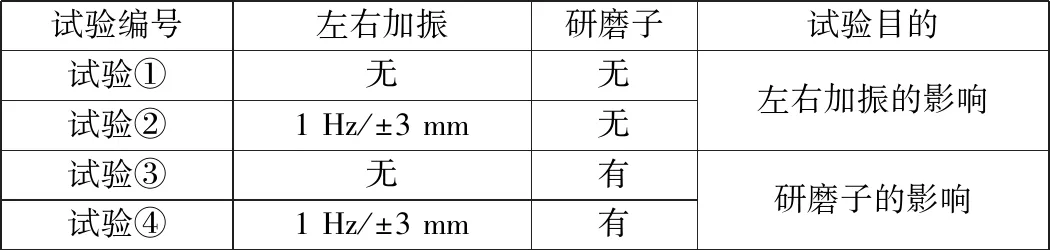
表1 磨耗試驗工況及目的

踏面磨耗速率隨走行距離的變化關系如圖3所示。圖3中：A區域對比了無加振條件下有、無研磨子對踏面磨耗率的影響；B區域顯示研磨子造成的踏面磨耗率；C區域對比了加振條件下有、無研磨子對踏面磨耗速率的影響。

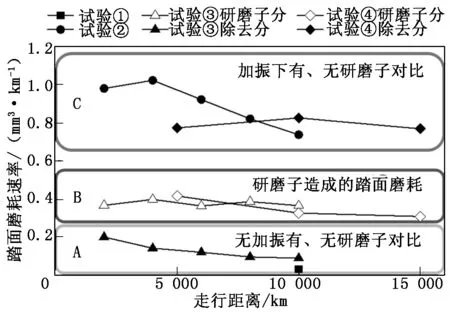
圖3 4組試驗的踏面磨耗速率曲線

A、C兩區域磨耗率差距明顯，可得出左、右激振是影響踏面凹坑磨耗的主要因素。

B區域中研磨子造成的踏面磨耗速率始終保持在0.4 mm3/km左右，沒有出現較大波動。該試驗中車輪載荷約為4 kN，按式(6)計算研磨子與車輪的比磨耗量為10-10mm2/N，故判斷出該試驗中研磨子與踏面的磨耗過程屬于定常磨粒磨耗，研磨子造成的磨耗體積與走行距離成正比關系。

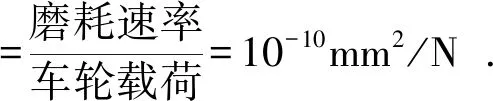
(6)

C區域中試驗②走行中后期磨耗速率發生大幅度降低，符合粘著磨耗率的變化特征；試驗④的磨耗曲線顯示踏面磨耗率始終在0.8 mm3/km附近小幅波動，未出現明顯降低趨勢，可以證明研磨子的加入影響了輪軌接觸向穩定磨耗階段的轉換，改變了輪軌磨耗的性質。

C區域中輪軌磨耗初期試驗④的磨耗速率比試驗②小得多，這是由于相比于輪軌前期磨耗率較大的磨合階段，研磨子在初期通過與車輪踏面的磨粒磨耗使得踏面上附著了大量研磨顆粒，阻止了踏面金屬材料與鋼軌之間的一部分粘著磨耗作用；隨著磨耗持續進行，踏面表面粗糙度不斷增加，輪軌粘著系數變大，磨耗速率相應緩慢增加，但隨著走行距離增加，踏面凹坑深度增加，研磨子表面和車輪凹坑內部材料接觸減少，故磨耗速率緩慢減小。

2 磨粒磨耗模型建立

輪軌潮濕時，研磨子在一定壓力作用下壓在車輪踏面上，可以在磨粒磨耗的作用下增加踏面表面微凸體的數量，提升踏面粗糙度；另外，研磨子摩擦過程中不斷脫落硬質顆粒并附著在輪軌接觸表面上，隨著車輪的轉動嵌入車輪和鋼軌之間，這些固體顆粒可以突破介于輪軌間的水膜，分擔一部分垂向載荷并提供縱向粘著力，提高粘著性能，研磨子的增粘功能通過與車輪的磨耗作用得以實現。基于上文對兩者磨耗類型的確定，在ABAQUS軟件中建立球形和圓錐形二維單磨粒磨耗有限元模型。

在研磨子的磨耗過程中車輪在強載荷下處于高壓和高應變率的狀態，故應用Johnson-Cook本構模型來近似模擬車輪材料的塑性變形行為，其表達式如下：

(7)

其中：σy為流動應力；εp為等效塑性應變；εr為應變率；εr0為準靜態應變率；T為當前溫度；Tr為室溫；Tm為熔點；A、B、C、m、n為應力應變參數，具體數值由實驗確定。表2為車輪鋼的力學性能和Johnson-Cook磨耗模型參數[8]。

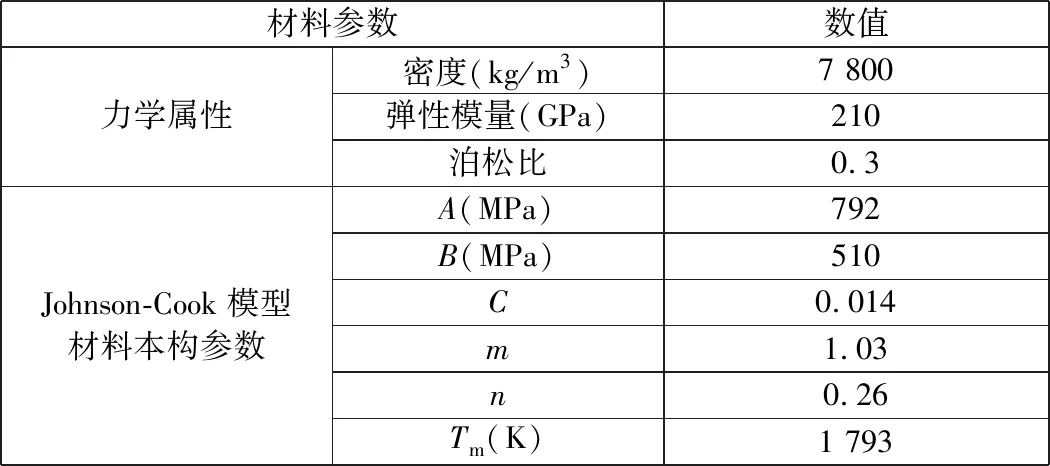
表2 車輪鋼的力學性能和Johnson-Cook磨耗模型參數

設置被磨材料長20 μm、高10 μm，剛性硬質磨粒的最大滑動距離為10 μm；相互作用選擇通用接觸，切向行為選取罰函數形式，法向行為選取硬接觸形式；除初始分析步外添加三個分析步，分別代表磨粒壓入材料、橫移劃擦和卸載過程。

對模型進行仿真后得到磨耗過程的應力應變云圖，如圖4～圖6所示。由圖4和圖5可以觀察到：球形磨粒在劃擦階段前方及下方材料的塑性應變應力相比于壓入階段較為嚴重，表面材料受到接觸應力的擠壓作用后沿橫向劃擦方向發生了明顯的塑性流動，這部分材料已發生嚴重的塑性變形，很容易在下次劃擦作用中被磨去；磨粒卸載后材料表面可以發現存在殘余應力以及顯著的塑性變形。

圖4 球形磨粒磨耗過程材料等效塑性應變云圖

圖5 球形磨粒磨耗過程材料等效應力云圖

由圖6可觀察到：圓錐形磨粒使材料表面形成隆起，前期并未出現材料流失現象，即處于犁耕階段；中后期磨粒繼續推動前方材料產生堆積現象，部分材料受到的應力超過其屈服極限后發生嚴重塑性變形，在明顯的顯微切削作用下產生切屑。

圖6 圓錐磨粒磨耗過程材料等效應力云圖

3 研磨子磨耗增粘過程的關鍵參數

磨粒磨耗過程中劃擦法向力和切向力決定了研磨子的磨耗增粘效果，依次改變模型參數觀察劃擦切向力的變化。

3.1 研磨速度

設置磨粒壓入深度為1 μm，摩擦因數為0.4，磨粒研磨速度分別為50 m/s、100 m/s、150 m/s、200 m/s，得到的研磨速度對磨粒磨耗的影響如圖7所示。由圖7可知：不同速度下劃擦法向力及切向力的最值和變化規律基本一致，但研磨速度較低時可以在較長時間內維持穩定的磨耗效果，而研磨速度較高時劃擦力變化幅度較大，更容易產生非均勻磨耗。研磨子更適合在盤式制動過程中同步作用于車輪踏面以降低磨耗量并起到協同制動的作用。

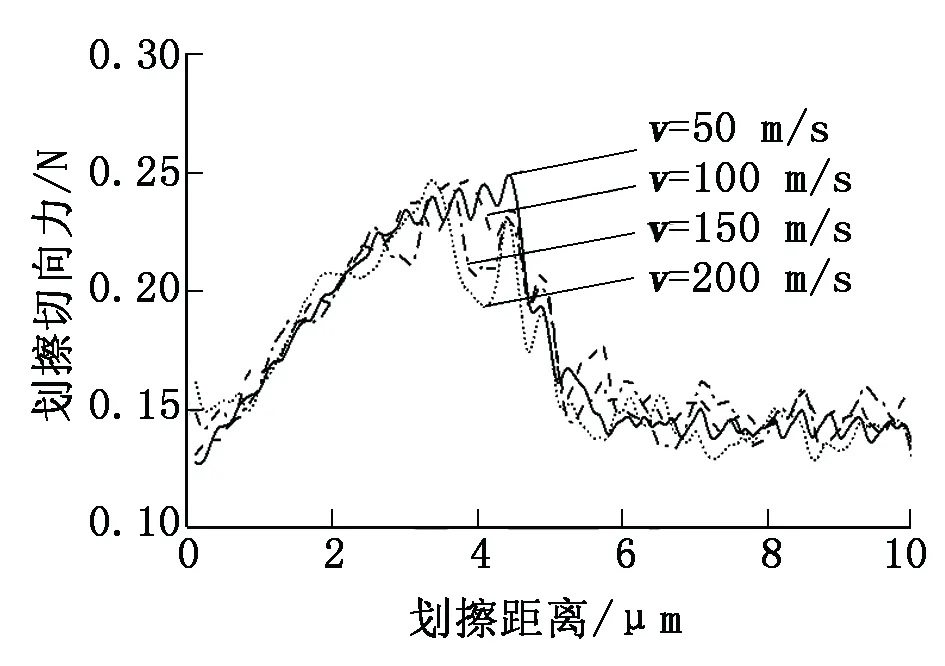
圖7 研磨速度v對磨粒磨耗的影響

3.2 壓入深度

設置磨粒研磨速度為50 m/s，摩擦因數為0.4，磨粒壓入深度分別為0.5 μm、1 μm、2 μm、3 μm、4 μm，得到的壓入深度對磨粒磨耗的影響如圖8所示。由圖8可知:隨著壓入深度的增加，磨粒與被磨材料的接觸面積增大，兩者之間的摩擦擠壓作用力也相應增大;壓入深度越小，磨耗就越先進入到穩定階段，即劃擦力與材料內部應力相互平衡的階段;此外，h=3μm和h=4 μm兩種工況的劃擦力的變化趨勢基本相同，此時對于半徑為5 μm的磨粒來說壓入載荷及深度過大，材料堆積和應力集中現象嚴重，劃擦力呈異常上升趨勢，車輪表面會形成明顯的塑性流變層從而加重塑性變形，出現異常磨耗。實際應用中應注意在研磨子可以實現功能的前提下施加適當的作用壓力。

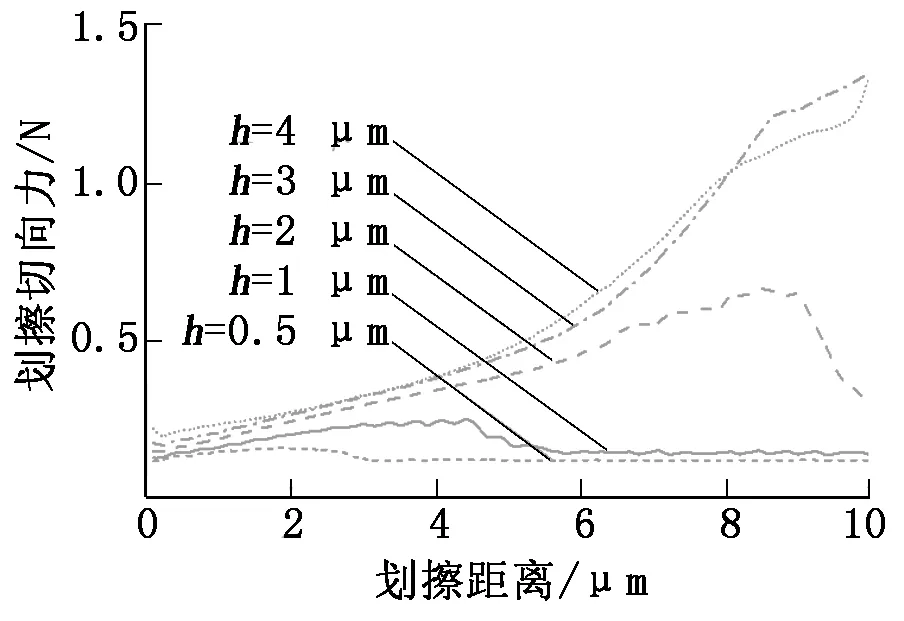
圖8 壓入深度h對磨粒磨耗的影響

3.3 摩擦因數

設置磨粒研磨速度為50 m/s，壓入深度為1 μm，磨粒與被磨材料間的摩擦因數分別為0.3、0.4、0.5,得到的摩擦因素對磨粒磨耗的影響如圖9所示。由圖9可以看出：隨著摩擦因數增大，被磨材料表面微凸體增多，作用于材料的劃擦力按一定比例增大，更容易產生殘余應力進而產生磨屑。

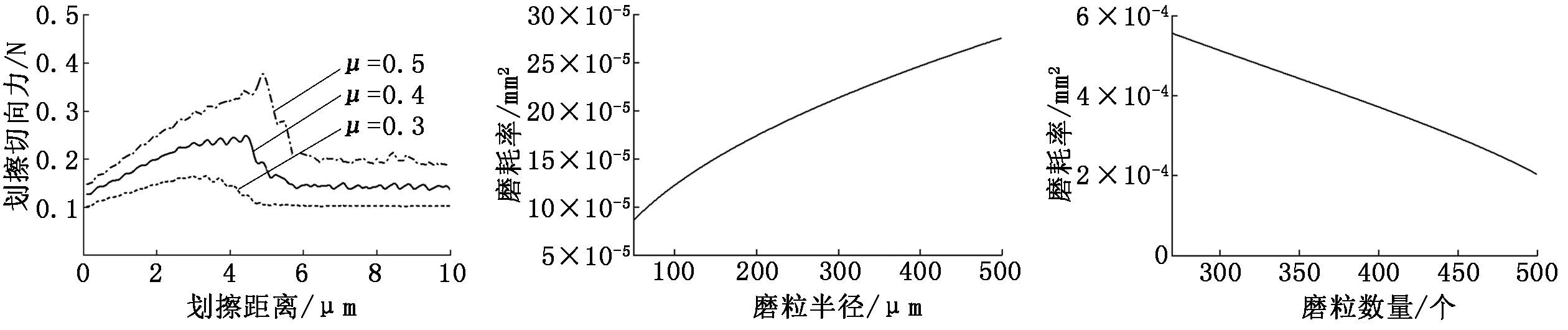
圖9 摩擦因數μ對磨粒磨耗的影響 圖10 磨粒半徑對磨粒磨耗的影響 圖11 磨粒數量對磨粒磨耗的影響

3.4 磨粒半徑及數量

Roylance等[9]通過試驗得到了磨粒數量N和磨粒半徑R的關系式N=555e-0.36R。根據前述磨耗率公式(5)畫出球形磨耗過程中磨粒半徑和磨粒數量對磨耗率的影響曲線，如圖10和圖11所示。從圖10和圖11可以看出：磨粒磨耗率隨著磨粒半徑的增大而增大，增速逐漸減緩；而隨著磨粒數量的增加而減小。這是因為在磨粒總體積不變的情況下磨粒數量增多后磨粒尺寸減小，單個磨粒的作用力減小；同時磨粒與被磨材料接觸不充分，起到了固體潤滑劑的作用。可以推測：在保證磨粒尺寸不變的情況下，初始階段磨耗率隨著磨粒數量的增多而增大，但后期磨耗率基本維持定值。

4 結論

(1)基于對研磨子與車輪踏面磨粒磨耗過程的判定，利用ABAQUS軟件分別建立了球形及圓錐磨粒磨耗模型，對比分析了研磨子磨耗增粘過程中車輪材料的應力應變的變化過程。

(2)分析了研磨過程中關鍵參數研磨速度、壓入深度、摩擦因數、磨粒半徑及數量對磨耗過程的影響規律，為研磨子作用參數的優化和控制策略的制定提供了依據。