基于剩余強度退化的FPSO系泊系統疲勞時變可靠性評估

趙 巖，余建星，2，余 楊，王華昆，王福程

（1.天津大學a.水利工程仿真與安全國家重點實驗室；b.天津市港口與海洋工程重點實驗室，天津 300072；2.北部灣大學機械與船舶海洋工程學院，廣西 欽州 535011）

0 引 言

浮式生產儲油卸油裝置（FPSO）通過系泊系統定位于某一特定海域，服役時間往往長達幾十年，屬于永久系泊范疇，對于永久系泊的海上結構物，因系泊鏈長期受到外部環境條件變化引起的循環載荷作用，將引起疲勞損傷，因此有必要對其進行疲勞壽命分析。

可靠性是評價構件的重要設計指標，尤其適合不確定性較強的海洋工程結構設計。Wirsching等[1]綜述了一些疲勞可靠性研究成果，研究了海洋結構物設計中疲勞可靠性方法的應用，該類基于SN曲線與線性疲勞累積準則的傳統方法被廣泛應用于海洋工程結構疲勞可靠性研究[2]，但此類方法尚未考慮可靠性的時變性。而在實際中，由于強度和載荷的不確定性、強度的退化等，強度和載荷的相對關系在不斷地發生變化，零部件和系統的可靠度和失效率顯然應隨載荷的作用次數或使用時間而變化，時變性是構件強度的典型特征。

在海洋工程領域，時變可靠性指標為構件的設計提供可靠依據，且有助于制定針對性的檢修方案，具有良好的工程實用價值[3]。當前時變可靠性模型的建立大多考慮了腐蝕的影響[4-6]。而在疲勞時變可靠性方面，余建星等[7]基于設計壽命可靠性理論對張力腿平臺建立了時變可靠性評估模型；劉勇等[8]基于首次超越失效準則計算了老齡導管架平臺，建立了時變可靠性模型，兩者均基于Miner線性累積損傷理論的破壞準則。目前對基于剩余強度退化機理的疲勞時變可靠性研究較少，且集中于機械構件的結構可靠性[9]。如王正等[10]基于一種構件抗力衰減模型、載荷強度干涉理論，考慮載荷與初始構件抗力不確定性，建立了機械構件疲勞時變可靠性模型；方永鋒等[11]在該模型基礎上建立了多次隨機載荷作用下的結構時變可靠性預測的概率密度演化方法。

本文在以上研究的基礎上，首次將剩余強度退化的時變可靠性模型與海洋工程疲勞計算結合，以內轉塔式FPSO系泊系統為例，給出一種多工況、風浪流聯合作用下的FPSO系泊系統時變可靠性評估方法。

1 疲勞時變可靠性分析方法

1.1 剩余強度退化理論

在循環疲勞載荷作用下，構件材料內部的損傷不斷累積，疲勞損傷的發展必然會引起材料內部微觀結構的變化，使材料的靜態力學性能退化。迄今不少學者已基于試驗研究提出了多種剩余強度退化理論[12]，本文選用文獻[13]提出的對數退化模型：

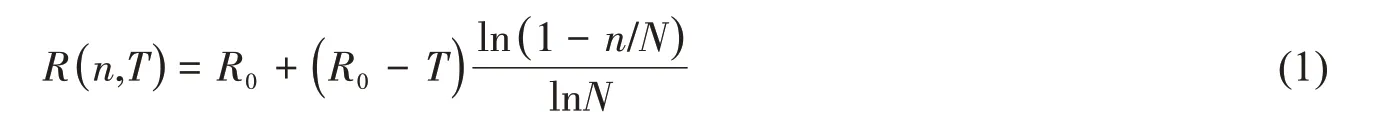
式中，R()n,T為拉力變程T的循環載荷下加載n次后的剩余強度；R0為初始強度；N為在拉力變程T的常幅循環載荷作用下的疲勞壽命，對于系泊鏈，該值可以在T-N曲線上獲取：

式中，K、M為T-N曲線參數。

對于變幅載荷，文獻[14]建立了多級載荷作用下剩余強度的等損傷比估計方法模型，將變幅載荷作用等效為恒幅載荷，本文參考其方法，獲得了任意兩級載荷等效公式：

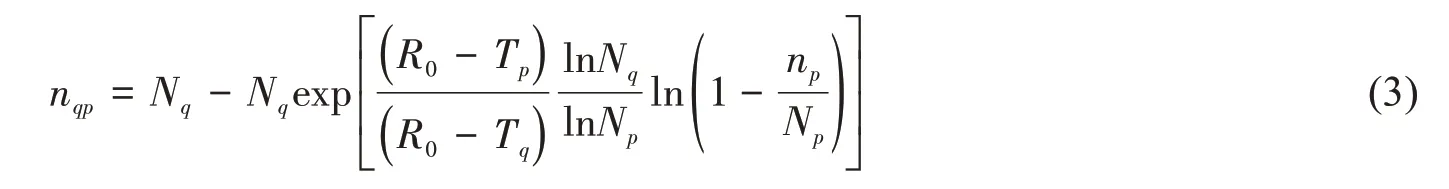
式中，p和q為任意載荷級數，即在載荷Tp作用下經歷了np次循環，其造成的損傷若換算成載荷Tq作用時，載荷Tq需經歷nqp次循環才能達到同樣的損傷。

考慮海洋工程載荷的強隨機性，通過雨流計數法進行計數的海洋工程載荷，各級載荷變程范圍較大。本文引入基準載荷以簡化計算，可得到多級循環載荷作用后的剩余強度為

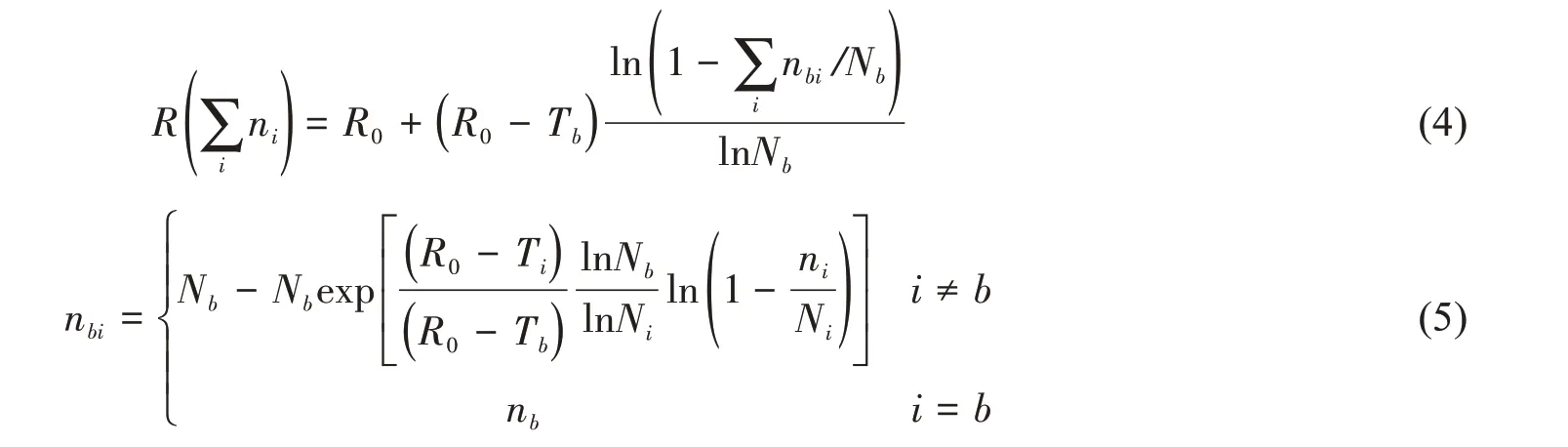
式中，ni為第i級載荷的循環數，b為基準載荷級數。

海洋結構物工況的長期狀態通常看成是由許多短期工況的序列所組成，則在多種工況下的單位時長的疲勞等效循環數為

式中，nequk為k工況下單位時長疲勞等效循環數，pk為短期海況出現頻率。

不考慮海洋環境的變化與每一單位時長內的構件抗力衰減，可以得到第ω單位時長內的構件強度為

1.2 載荷分布估計模型

在單位時間內，載荷的最大值超過構件剩余強度即認為構件失效。為確定載荷最大值的概率分布，提取每種工況研究時段的所有極大值點并統計各級載荷出現頻率，多工況加權后可得到長期載荷極大值的頻率分布，可認為其近似符合正態分布，獲取其分布參數。

而單一研究時段的最大值即為所有極大值中的最大值，文獻[15]認為多個相同正態分布變量的最大值符合極值I型分布（Gumbel分布），其分布函數為

式中，a為尺度參數，b為位置參數。

式中，μ為正態分布均值，σ為正態分布標準差，n為正態分布變量數。

1.3 以研究時段為壽命度量指標的構件時變可靠性

文獻[16]推導了以載荷次數為壽命度量指標的構件時變可靠性公式，但海洋工程中計算時長較長，以載荷次數計算過于消耗計算力。本文將總計算時段分散為多個研究時段，每個研究時段時長為一個單位時間，假設在每一研究時段內，構件的性能不發生退化。

定義ω單位時間的時變可靠性為經過ω單位時間，構件未發生失效的概率，參考文獻[16]中的方法，其可由式（11）得出：

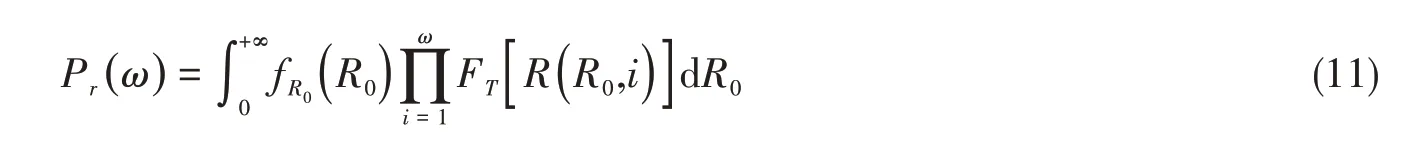
從ω1單位時間至ω2單位時間未發生失效的概率即為

2 計算模型與討論

2.1 計算模型參數

時域耦合分析采用由DNV開發的、內置Simo-Riflex計算模塊的Sima軟件進行。以內轉塔式FPSO為例，平臺總重為148 200 t，船長為300 m，船寬為60 m，吃水為18.75 m。系泊鏈采用R3級無檔錨鏈，分布形式采用對等分布，其布置如圖1所示，系泊鏈參數見表1。

圖1 系泊系統布置Fig.1 Sketch of the mooring system

表1 系泊系統主要參數Tab.1 Main particulars of mooring systems

根據Qian[17]的研究，構件的初始強度符合對數正態分布，其概率密度函數如下：

其分布參數可通過試驗獲得，本文取μ=15.063，σ=0.01。

風浪流環境如下：計算水深為320 m，風譜采用NPD風譜，平均風速為11.4 m/s，表層海流速度為0.5 m/s，風浪流方向均為180°。波浪采用Jonswap雙波峰譜，為了數值模擬的需要，將南海某海域波浪散布圖[7]根據平均波高、周期分為24種海況，如表2所示。

表2 24個短期海況Tab.2 24 short-term conditions

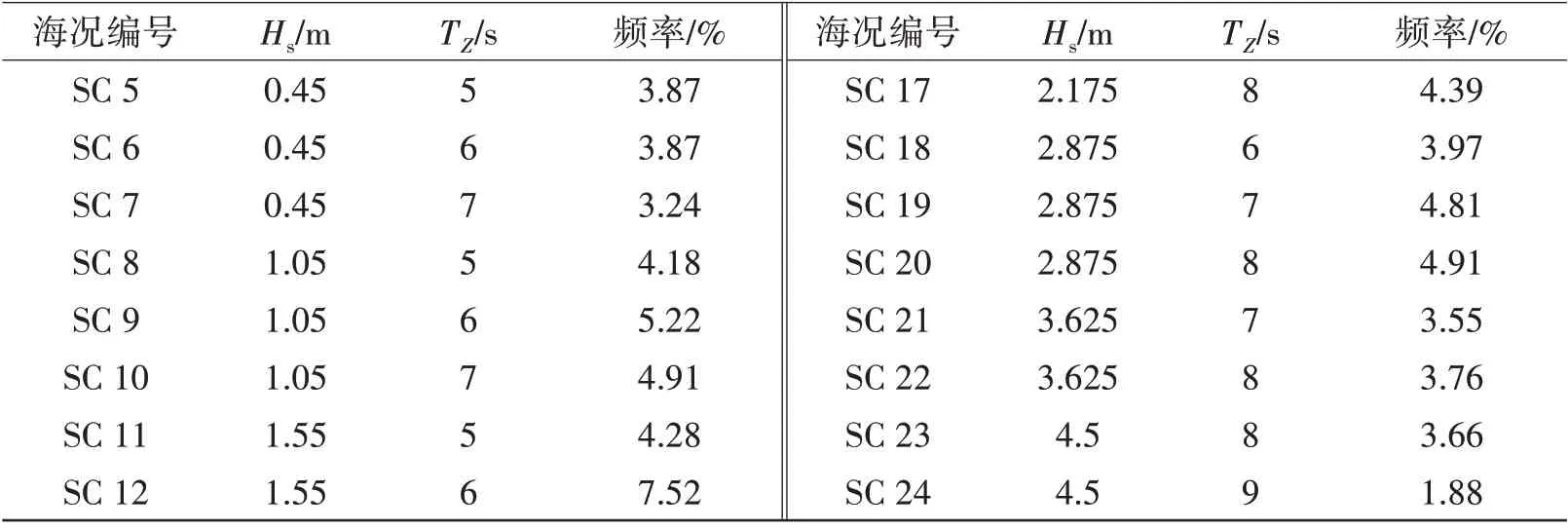
續表2

2.2 時變可靠性計算與討論

提取水動力計算結果，取系泊鏈頂端節點作為關鍵節點，其受力時程曲線如圖2所示，數值模擬計算時段時長選為10 800 s，并作為可靠性計算的單位時長。

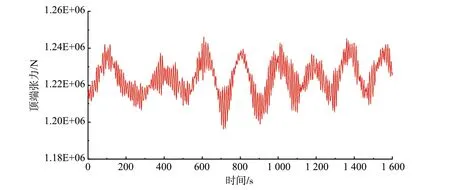
圖2 系泊鏈頂端張力曲線Fig.2 Time history of mooring chain top tensile force

應用雨流計數法對圖2時程曲線進行計數，應用1.2節方法獲取載荷的概率分布函數，初始強度的概率密度函數如式（13），不考慮檢修和測試的影響由式（11）算得各系泊鏈頂點疲勞時變可靠性,如表3所示，以可靠性指標β表示。

表3 各時間段的可靠性指標Tab.3 Reliability index during each period

2.3 早期測試對疲勞可靠性的影響

由表3可見，各系泊鏈疲勞可靠性有清晰的下降趨勢，但其各時段可靠性指標極低，主要是因為未考慮平臺服役前的多種測試，該結果無法被接受。而考慮到平臺在正式測試進入工作狀態前，通常需要在近海進行測試，則不考慮前6個月測試期內失效獲得的結果更具有實際意義，各系泊鏈頂點疲勞時變可靠性指標如表4所示。

表4 考慮早期測試的各時間段的可靠性指標Tab.4 Reliability index during each period with early test

定義第i年可靠性為第i-1年未發生失效的前提下，在第i年也未發生失效的概率。選取典型的系泊鏈1、4、7和11，以可靠性指標β表示的時變可靠性、年可靠性變動如圖3和圖4所示。

圖3 時變可靠性曲線Fig.3 Time-dependent reliability curves

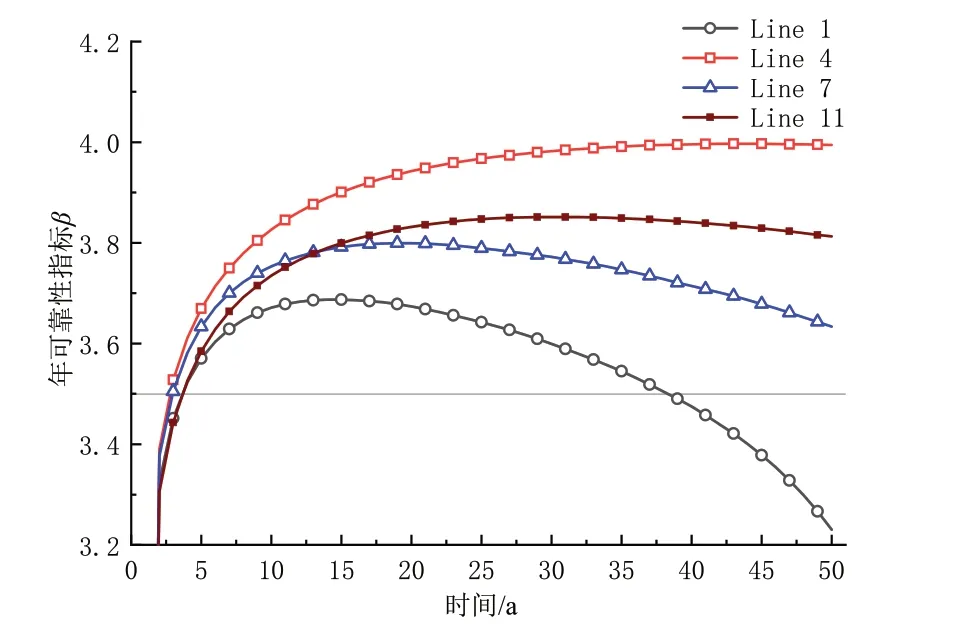
圖4 年可靠性變動曲線Fig.4 The ith-year reliability change curves

根據時變可靠性下降速率可將研究時段分為三個時期：早期（約1～3年），由于構件強度和載荷的不確定性較強，系泊鏈疲勞時變可靠性快速下降，此階段需要對構件進行監控、更換不合格構件，通常為試驗期；中期（約4～39年），構件強度經過早期的驗證，不確定性降低，可靠性下降速率趨于平穩，此階段運行相對安全，檢修成本也較低；后期（約40年后），由于疲勞累積導致構件的剩余強度下降效果開始明顯，可靠性下降速率增大，部分系泊鏈在短時間內疲勞可靠性快速下降，面臨較大失效風險，此階段平臺趨于老齡、安全性下降，需要加強檢修。文獻[18]將這三種時期稱為“早期失效期”、“偶然失效期”和“耗損失效期”。

另外，由于不同節點的應力時程曲線不同，導致疲勞累積的速率不同，不同系泊鏈的時變可靠性曲線有相交，即表示在不同時期系泊鏈危險程序排序有變化。

2.4 早期測試時長的影響

2.3節給出了測試期為6個月的可靠性結果，為研究測試期時長對可靠性的影響，以其設計壽命20年的可靠性為標準，獲取不同測試時長下的20年可靠性指標，如表5所示。

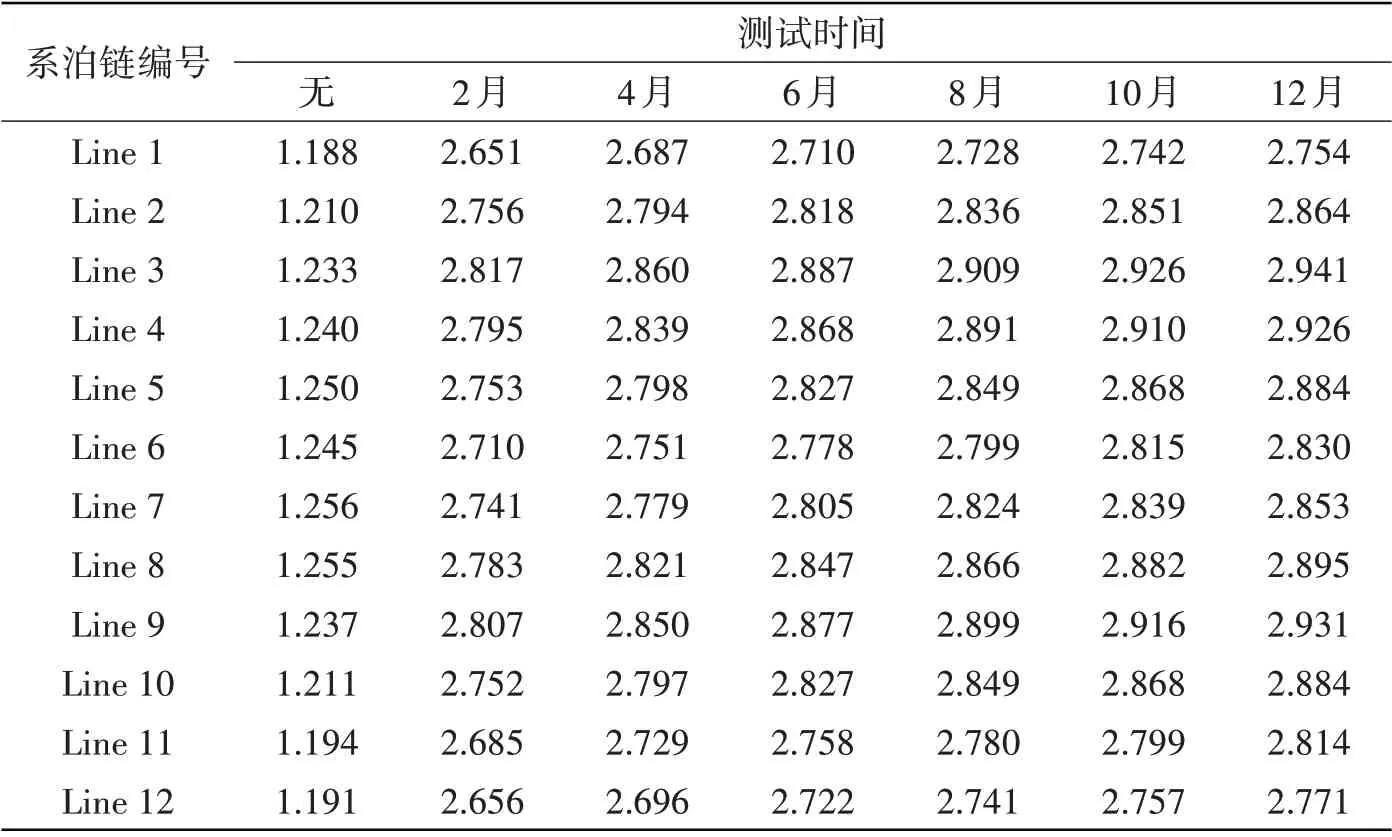
表5 不同測試時長下的20年可靠性指標Tab.5 20-year reliability under different testing times

與表3、表4中20年可靠性數據對比，可見早期的測試可以顯著提升其可靠性，同時單位增量測試時間內的提升效果隨著測試時間的增大而減小，考慮測試的經濟性可獲取最佳測試時長。

3 結 論

本文針對海洋工程構件疲勞可靠性問題，利用Sima軟件獲取其在復雜海況下的動力響應，考慮構件初始強度的不確定性、載荷的不確定性、構件強度的時變性，進行了海洋工程結構疲勞時變可靠性分析，通過分析認為：

（1）海洋工程疲勞可靠性具有顯著的時變性，不考慮檢修的情況下，構件可靠性指標呈現下降趨勢，且可靠性下降速率、系泊鏈危險程序排序在不同時間均有變化；

（2）根據疲勞時變可靠性下降速率可將服役期大致分為三個時期，各時期內的主要失效原因不盡相同，應針對每個時期建立不同的維護策略；

（3）早期測試可以顯著增加構件設計壽命內的疲勞可靠性，但隨著測試時長的增加，單位增量測試時長的提升效果減少。