內肋骨長艙段塑性總體穩定性計算方法研究

邱昌賢，黃進浩，秦 天，王 琨

（中國船舶科學研究中心，江蘇 無錫 214082）

0 引 言

由各國潛艇結構的現狀與發展趨勢可見，基于大分艙思想的單殼體長艙段結構形式是一種成功的設計方案，可顯著減少輕外殼、舷間結構及內部艙壁的重量和裝配、焊接施工量，并為大型設備、模塊化平臺的縱向進艙提供了極大便利，艙壁的減少也有利于線纜、管路的總體布置。單殼體圓柱殼艙段通常采用內肋骨形式，與外肋骨相比，避免了肋骨受海水雙面腐蝕的不利狀況，其翼緣應力有所增大，但結構總體穩定性理論上會比外肋更好，長艙段的長徑比（耐壓殼長度/直徑）往往比小分艙艙段大一倍以上，為保證總體穩定性，常設置一根或多根特大肋骨（heavy frame）進行加強，因此耐壓結構設計需要解決普通肋骨內置且帶特大肋骨的單殼體長艙段結構的總體穩定性計算問題。

20世紀中葉起，英國的Kendrick博士[1]曾基于薄殼穩定性理論研究了帶中部強肋骨的環肋圓柱殼外壓屈曲問題。美國Taylor水池進行過大分艙環肋圓柱殼的精車模型試驗研究[2]，采用14道工序將中部特大肋骨切削為不同的截面形狀，分別進行無破壞試驗（避免材料進入塑性），以檢驗具有不同扭轉、彎曲剛度的強肋骨的加強效果，試驗中基于彈性應變測量數據用Southwell法推算臨界壓力，該值與實際破壞壓力的誤差在4%以內[3]，驗證了強肋骨能代替重量大得多的內部艙壁對長艙段起到支撐作用。Baruch和Singer[4-5]研究了肋骨偏心對端部簡支圓柱殼彈性失穩壓力的影響，認為與外肋相比，內肋能將臨界壓力提高10%～15%。以上研究工作均局限于彈性穩定性范疇，雖然取得了很有價值的學術成果但工程實用性不強。

近年來，國內一些研究者基于規范方法和有限元分析，也得到了一些有意義的結論。丁海旭[6]對若干精車模型進行了彈性穩定性計算，給出了大肋骨與普通肋骨慣性矩之比與艙段總體穩定性的關系；何福志[7]對Taylor水池的長艙段模型進行了有限元分析，根據總體失穩壓力—框架肋骨慣性矩關系曲線搜索大肋骨最優結構參數；宋世偉[8]采用Abaqus分析了環肋圓柱殼長艙段的穩定性規律，研究了現行規范在不同參數范圍內的求解適用性；邱昌賢[9]基于矩形截面壓桿的雙模量理論和高強度鋼的材料彈塑性本構關系，建立了環肋圓柱殼結構總體穩定性塑性修正曲線及修正方法。

參照國內外文獻及研究經驗，針對現有方法的局限性，作者在結構上考慮肋骨偏心的影響，在材料上考慮高強度鋼的彈塑性本構關系，利用Ritz法對環肋內置且含特大肋骨的單殼體長艙段結構在靜水外壓下的彈塑性穩定性計算方法進行理論研究，分別基于J2流動理論和形變理論建立了結構小撓度彈塑性失穩壓力的迭代計算方法，編制了運算程序，針對長徑比為1.5～3.1的高強度鋼模型進行了理論計算和有限元數值仿真分析工作，獲得了塑性階段的模型總體失穩破壞壓力。本文方法給出的結構總體穩定性計算值與有限元結果符合較好，可使耐壓結構的尺寸和重量設計更為優化。本文的計算方法經初步驗證是合理和可行的，所得研究成果和相關結論可為單殼體長艙段結構的穩定性機理剖析提供技術支撐和參考建議，也為現行規范方法的修改完善及在設計中確定合理的尺寸參數和安全儲備打下了基礎。

1 圓柱殼長艙段結構彈塑性穩定性計算方法

1.1 彈塑性失穩系數

經典的材料塑性理論將單向拉伸曲線推廣到復雜的三維應力狀態，目前對塑性屈曲問題采用的本構關系主要有2種：塑性等向強化的J2流動理論（塑性增量理論）和J2形變理論（塑性全量理論）。增量理論建立應力增量和應變增量之間的關系，全量理論認為應力和應變存在一一對應的函數關系，二者均可通過引入彈塑性失穩系數[aij]來建立統一的廣義應力、應變關系[10-11]：

材料應變由彈性和塑性部分組成，其中彈性應變可由廣義Hooke定律得到：

獲得彈性應變增量的表達式后，再根據J2流動理論推導材料進入塑性后的應力應變增量關系，即可得到彈塑性應力—應變增量之間的關系式[10]：

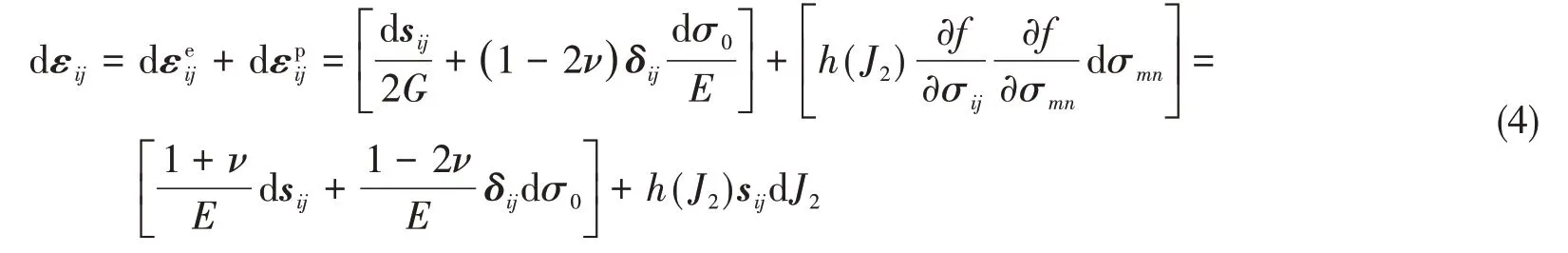
式中，h(J2)可由順x軸的單向拉伸試驗確定，σij在除x軸以外的方向為0，σ0=σx/3。

將εij（i，j=1，2，3）分別按式（4）展開可得6個方程，再代入式（3）～（4）等表達式進行變量代換，整理后可得對稱的彈塑性失穩系數矩陣[aij]（i，j=1，2，3，4，5，6）。

根據J2形變理論，材料應力、應變之間的彈塑性關系為

同理，將εij（i，j=1，2，3）展開后可得對稱的系數矩陣[aij]（i，j=1，2，3，4，5，6）。

全量、增量理論的彈塑性失穩系數矩陣[aij]形式相似，對潛艇耐壓圓柱殼結構，可忽略法向應力σz，則廣義三維應力狀態退化為平面應力狀態，再根據Kirchoff直法線假設，剪應力τzy、τzx為0，從而使[aij]的形式大為簡化。

為方便計算，假定失穩前耐壓圓柱殼處于無矩狀態，橫向剪應力τxy為0，計算周向應力時將肋骨截面積平均分配到殼板上，經推導可得具體形式進一步簡化的失穩系數[aij]，再用[bij]將應力-應變關系改寫為

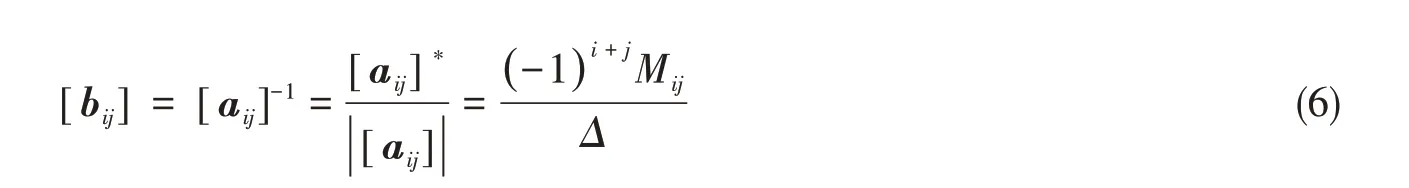
1.2 考慮肋骨偏心的塑性穩定性計算方法

塑性穩定性計算時取坐標原點在圓柱殼端部中曲面上，設x、y、z分別為縱向、周向和徑向坐標，u、v、w分別為縱向、周向和徑向位移，徑向坐標和徑向撓度均以指向圓心為正，圓柱殼失穩時滿足簡支邊界條件的形函數[10-14]取為

利用1.1節推得的彈塑性系數[bij]，結構按平面應力狀態并僅考慮小撓度，分別計算耐壓殼板的彎曲及中面應變能V1、V2的應變能：

普通肋骨及特大肋骨均可簡化為單向應力狀態，其位移函數與圓柱殼體相同。為考慮截面偏心影響，肋骨橫截面上任一點的周向應變值根據該點的徑向坐標來確定：

經推導，對距離坐標原點x=il處的第i根肋骨，其結構應變能為

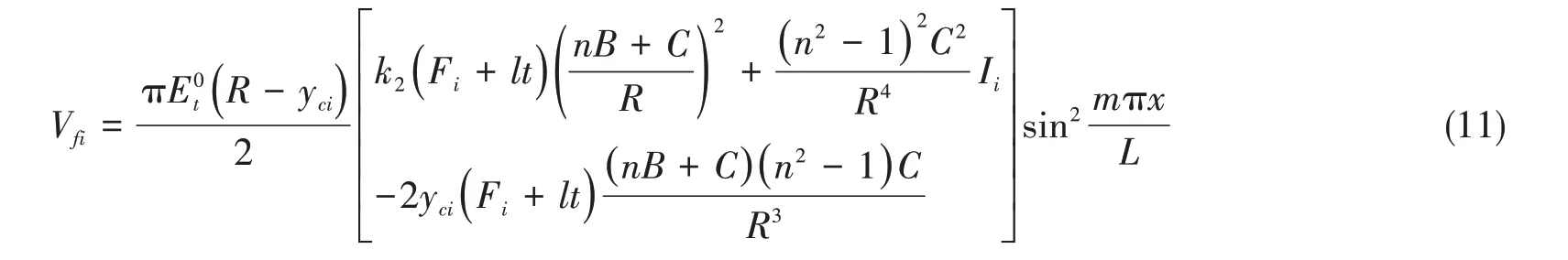
式中，yci為第i根環肋計及帶板寬度為l（特大肋骨取為與規范相同的2l）的組合截面形心的徑向坐標，Rfi為截面形心半徑，Ii為截面慣性矩，I0i為第i根環肋自身慣性矩，Fi為肋骨橫剖面面積，y0i為肋骨中和軸到殼板表面的距離，y0i+0.5t=efi，t為板厚。式中引入系數k2=1或0以分析肋骨壓縮應變能的影響。根據相關理論研究，肋骨截面的扭轉、翹曲和面外彎曲的應變能對環肋圓柱殼彈性失穩壓力的影響很小[2]，計算中予以忽略。

求得結構各部分能量后再計算水壓做功，從而可建立能量平衡方程。根據能量原理，結構總能量П取極小值的條件是П對A、B、C的偏微分為0，由此得到如下齊次線性方程組：

此方程組存在非零解的充要條件是系數行列式為0，這個矩陣是對稱的，cij=cji。

利用能量法計算單殼體長艙段結構的彈塑性失穩壓力時，首先將割線模量Es和切線模量Et取為彈性值，則[bij]退化為彈性失穩系數，求得與彈性臨界壓力對應的等效應力強度，若高于材料比例極限，則在附近選定一個應力強度計算相應的Es和Et（Es和Et可根據高強度材料單向拉伸試驗的彈塑性本構關系確定），再通過迭代求解塑性失穩壓力。

帶特大肋骨的單殼體長艙段結構的彈塑性總體失穩形式既可能表現為含大肋骨的艙段失穩（一般周向整波數n=2），也會發生在大肋骨之間的艙段上（一般周向整波數n=3）。本文的計算方法對以上二者均可適用，并可方便地推廣至含多根大肋骨艙段的穩定性計算，或退化為無大肋骨艙段的狀態。

2 模型計算結果對比分析

為了驗證理論方法，對內肋骨長艙段模型進行了有限元建模和數值計算，其結構形式為T型內環肋圓柱殼，舯部采用內置T型特大肋骨加強，大肋骨根部耐壓殼板進行了局部加厚，材料為高強度鋼。所計算模型的主要結構參數為：艙段長徑比L/D=3.14，特大肋骨與普通肋骨慣性矩比Ihf/If=41.42，圓柱殼半徑與厚度之比R/t=106.75。

本文利用所建立的方法和程序對圓柱殼長艙段模型的結構塑性總體穩定性進行了計算，迭代算法收斂速度很快且結果精度較高，如圖1所示。

圖1 長艙段結構塑性穩定性迭代計算中各子步誤差Fig.1 Error value in every substep of the buckling calculation

為評估理論計算方法的合理性，本文還采用了形式較為簡潔的規范公式、修正曲線和ANSYS有限元程序進行計算，并展開結果對比，如圖2和表1所示。

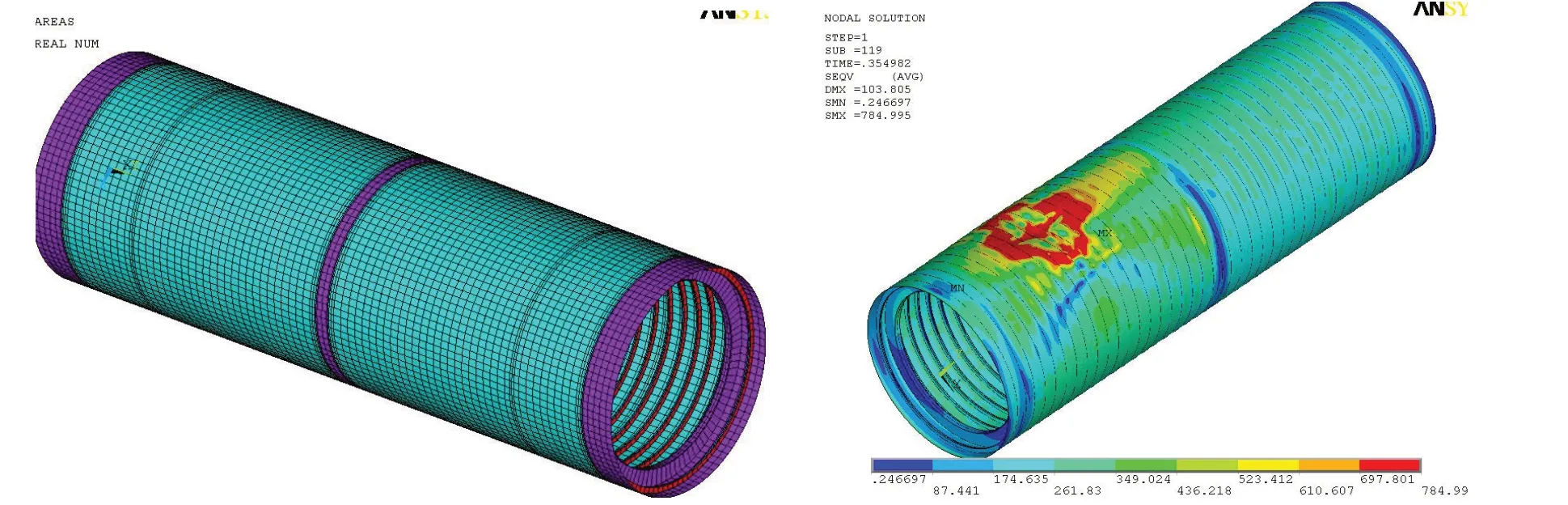
圖2 單殼體長艙段結構有限元模型及塑性總體失穩數值計算結果Fig.2 FE shell model and numerically-analyzed results for general instability

表1 模型塑性總體失穩壓力計算結果（MPa）Tab.1 Models’calculated critical pressure of plastic general stability(MPa)

對于大肋骨之間的艙段塑性總體穩定性，與有限元結果相比，規范計算值偏保守一些，本文理論方法的計算值接近且略高于有限元分析結果，初步驗證了方法是合理、可用的，4個算例的結果表明，流動理論與形變理論的計算結果有所不同，但差別不大。

對于包含舯部特大肋骨在內的模型結構塑性總體穩定性，與有限元解相比，失穩臨界壓力的規范解（8.37 MPa）略偏保守，導致為了滿足總體失穩壓力的控制標準，需額外提高特大肋骨的剛度，由此產生的冗余重量和尺寸將不利于結構優化和設備布置。本文理論方法的計算值相對合理，若能保證其可靠性，則可使耐壓結構的尺寸和重量設計更為優化，但該方法尚需得到更多試驗結果的驗證和支撐。

3 結 語

本文參照國內外研究經驗，針對現有方法的局限性，在結構上考慮肋骨偏心的影響，在材料上考慮高強度鋼的彈塑性本構關系，利用Ritz法對環肋內置且含特大肋骨的圓柱殼長艙段結構在靜水外壓下的彈塑性穩定性計算方法進行了理論研究；基于流動理論和形變理論建立了結構小撓度彈塑性失穩壓力的迭代計算方法，計算結果精度較好，工程實用性較強；同時針對長徑比為1.5～3.1的高強度鋼模型進行了有限元數值仿真分析，計算和對比了塑性階段的模型總體失穩破壞壓力，本文方法給出的結構總體穩定性計算值與有限元結果符合較好。

本文理論計算方法經初步驗證是合理和可行的，給出的總體失穩壓力計算值比規范方法更符合高強度鋼模型有限元計算結果。方法的通用性較好，既可方便地推廣至含多根大肋骨艙段的穩定性計算，也能退化為無大肋骨艙段的狀態。圓柱殼長艙段結構的總體失穩形式無論是包含大肋骨的艙段失穩，還是在大肋骨之間的艙段失穩，規范方法給出的計算結果都比較保守，從而導致結構增加冗余重量和尺寸。本方法可使耐壓結構的設計更為優化，但方法的可靠性尚需得到更多試驗結果的驗證和支撐。

按單向應力狀態計算肋骨應變能的方法在肋骨腹板增高后或存在適應性問題，特大肋骨自身的側向穩定性機理尚待研究，內、外肋骨圓柱殼總體穩定性的差異需要模型試驗的充分驗證。關于幾何非線性對結構彈塑性穩定性的影響，本文沿用了規范的修正方法，建議在此領域開展深入探討。結構大撓度的影響也需進一步研究。