全橋LC-LC 串并聯諧振逆變器小信號建模及閉環設計

張 彬，羅全明

（1.重慶航天職業技術學院電子工程系，重慶 400021；2.重慶大學電氣工程學院，重慶 400044）

LED 作為新一代綠色照明光源，已在道路照明、景觀照明、LCD 背光等大功率LED 照明領域得到了廣泛的應用[1-6]。在大功率LED 照明領域，LED 驅動電源至少須實現功率因數校正、輸入輸出隔離和多路恒流輸出三大功能[7-8]。兩級多路恒流輸出LED 驅動電源具有結構簡單、元器件少、效率高等優點，是目前LED 驅動電源領域研究的重點之一，主要由前級功率因數校正器和后級隔離型多路LED 恒流驅動器構成。

文獻[9]提出的隔離型多路LED 恒流驅動器由高頻DC/AC 逆變模塊和高頻AC/DC 整流模塊通過高頻交流母線組合而成，實現輸入輸出電氣隔離及多路恒流輸出兩大功能。高頻DC/AC 逆變模塊采用恒頻移相控制全橋LC-LC 串并聯諧振逆變器，將直流輸入電壓（即功率因數校正器的輸出）變換為高頻交流電壓并通過一個兩繞組變壓器實現輸入輸出隔離。高頻AC/DC 整流模塊采用無源諧振恒流網絡，內部僅包括電感、電容、二極管等無源器件，在頻率與幅值一定的高頻交流電壓驅動下可以實現單位功率因數及恒流輸出，通過多個無源高頻AC/DC 整流模塊實現多路恒流輸出。本文主要研究高頻DC/AC 逆變模塊，由于其采用的恒頻移相控制全橋LC-LC 串并聯諧振逆變器性能分析及優化設計在文獻[10-11]中已有詳細的闡述，所以不再贅述，只主要分析其動態性能，并對其進行建模分析和閉環設計。

變換器的大信號模型反映了其穩態特性，并為其在穩態工作時的分析和主電路參數設計提供依據，而小信號模型則反映了其在穩態工作點附近受到小信號擾動（如控制信號變化、負載擾動、輸入電壓波動等）時，電路中各變量的變化規律，變換器的小信號模型是控制系統設計的基礎。對于一般變換器而言，如脈沖寬度調制PWM（pulse width modulation）變換器，狀態空間平均法[12]得到了廣泛的應用，該方法利用系統狀態變量時間連續的概念，在開關頻率足夠高時，忽略一個開關周期中輸入信號的變化，以開關平均的概念將變換器用一個線性時不變的狀態方程來近似，然后利用解析方法對其進行建模。通過狀態空間平均法，PWM 變換器的小信號特性可以方便地推導出來。然而，對于諧振變換器而言，其開關頻率非常接近諧振網絡的自然諧振頻率，并且其狀態變量中主要包含開關頻率諧波，而不是PWM 變換器中的低頻分量。當系統開關頻率與諧振網絡的自然諧振頻率接近時，狀態空間平均法便無法應用。諧振型變換器可通過離散采樣數據來獲得小信號模型[13-14]，由于該方法得到的離散模型必須進行數值求解，結果不夠直觀，而且當諧振元件數量增加時，分析變得非常復雜，因此很難得到廣泛應用。離散時域仿真法[15]利用狀態空間法列出非線性系統的分段線性方程，找出狀態轉移規律，得出非線性差分方程，用計算機進行求解，該方法可以得到較精確的模型，但是這種仿真法得不到解析形式的數學方程，必須完全依靠計算機的數值計算分析，物理概念不清晰。

針對上述小信號建模方法的不足，本文采用相量建模法PDM（phasor-domain modeling）[16-18]對恒頻移相控制全橋LC-LC 串并聯諧振逆變器的小信號模型進行分析，通過將時域量變換到相量域，可以得到諧振逆變器的相量域大信號模型，再加入小信號擾動后即可得到相量域的小信號模型。由于諧振逆變器的相量域模型與其時域模型具有緊密相關性，因此保持了其狀態變量的物理特性。利用相量建模法得到高頻諧振逆變器的小信號模型物理概念清晰、模型準確、簡單方便。最后通過仿真及實驗驗證模型的正確性，實驗結果表明，經過閉環控制，諧振逆變器具有良好的抗輸入電壓和負載變化擾動的能力，能夠達到預期的效果。

1 工作原理

全橋LC-LC 串并聯諧振逆變器主電路如圖1所示，包括由開關管S1—S4構成的全橋開關網絡、由Ls、Cs、Lp、Cp構成的LC-LC 串并聯諧振網絡以及高頻變壓器T。

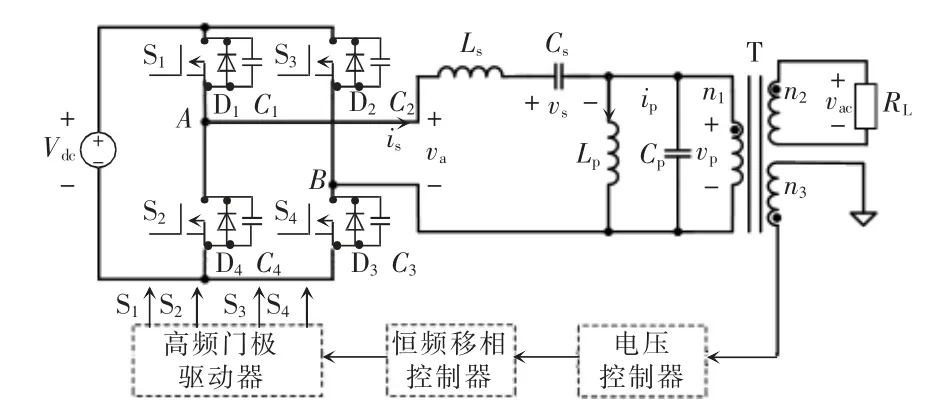
圖1 全橋LC-LC 串并聯諧振逆變器主電路Fig.1 Main circuit of full-bridge LC-LC series-parallel resonant inverter

LC-LC 串并聯諧振網絡具有良好的濾波性能，可確保輸出高頻交流電壓的總諧波含量THD（total harmonic distortion）低于5%，此外，如果其自然諧振頻率略低于開關管的開關頻率，可在寬輸入輸出范圍實現開關管的零電壓開通，因此，可以工作在高頻狀態，進而提高功率密度。同時，通過恒頻移相控制，可確保其輸出高頻交流電壓頻率及幅值恒定。高頻變壓器不但可以實現輸入輸出電氣隔離，而且也可以使開關管在輸入電壓寬范圍變化時的零電壓開通更容易實現。由于本文高頻DC/AC 逆變模塊的后級無源高頻AC/DC 整流模塊在頻率與幅值一定的交流電壓驅動下可以實現單位功率因數校正功能以及恒流輸出功能[9]，因此，在對全橋LC-LC串并聯諧振逆變器進行分析與設計時，可以將其所接的無源高頻AC/DC 變換模塊用電阻RL替代。

為了得到頻率與幅值恒定的高頻交流電壓，須采用恒頻移相控制PSM（phase shift modulation）。所謂PSM 是指在保證頻率恒定的前提下，通過對稱開關橋臂相位的移動來調節開關網絡輸出電壓va的脈寬，進而實現對高頻交流輸出電壓vac幅值的調節。在穩定工作時，恒頻移相控制全橋LC-LC 串并聯諧振逆變器中每個開關管的占空比小于50%，其中上下橋臂的開關管互補導通，通過調節2 個橋臂中的下開關管相位即可調節開關網絡輸出電壓va的基波分量，進而控制輸出高頻交流電壓vac的幅值，而輸出電壓的頻率即為開關頻率。

圖2 為實現恒頻移相控制功能主要部分的模擬電路，由圖2 即可以推導得出恒頻移相控制的波形，如圖3 所示。

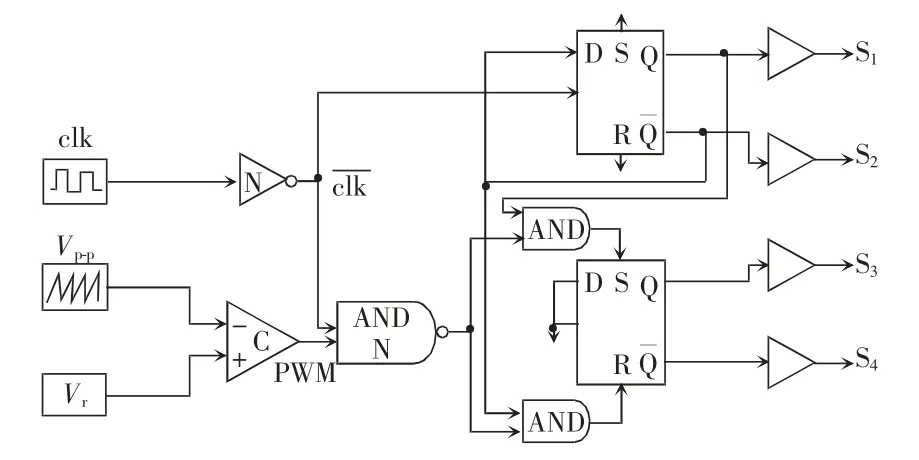
圖2 恒頻移相控制電路Fig.2 Constant-frequency phase shift modulation circuit

圖3 恒頻移相控制實現波形Fig.3 Operation waveforms under constant-frequency phase shift modulation

由圖3 可以看出，當載波信號頻率與幅值一定時，輸出參考電壓的波動即可使得開關管的驅動脈沖發生相位移動，進而實現開關網絡輸出電壓脈寬的變化。其調節方式與傳統的變占空比調節的變換器的控制思想一致，即通過在恒頻移相驅動前加入PI 或者PID 等調節器，即可以實現高頻交流電壓的穩定輸出。

在采用相量建模法進行分析之前，需要將時域量變換到相量域，根據文獻[16-18]，對于電感L 來說，加在其兩端的正弦交流電壓VL和通過其內部的正弦交流電流IL在相量域中的關系可以表示為

同理，對于電容C，加在其兩端的正弦交流電壓VC和通過其內部的正弦交流電流IC在相量域中的關系可以表示為

同理，對于電阻R，加在其兩端的正弦交流電壓VR和通過其內部的正弦交流IR電流在相量域中的關系可以表示為

對于相量域的電壓和電流來說，其是由有功分量和無功分量組成。因此，對于電感在相量域的電流和電壓可以表示為

將式（4）與式（5）代入式（1）中，可以得到

同理，對于電容和電阻，可以得到

2 全橋LC-LC 諧振逆變器相量域大信號模型

為了更好地研究其小信號模型，首先對其大信號模型進行研究與分析。選擇諧振網絡中的電感Ls、Lp的電流is、iLp，電容Cs、Cp的電壓vCs、vp為狀態變量。假設在此設計中各個元器件均為理想元件，不考慮其寄生參數，由圖1 電路可得

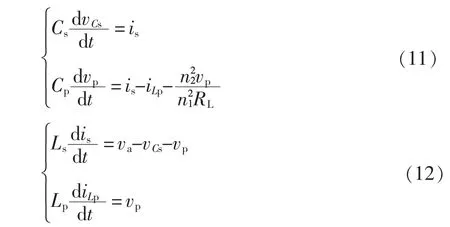
由式（11）和式（12）可得狀態方程

圖1 的LC-LC 串并聯諧振逆變器電路在任何角頻率下，其時域的狀態空間變量都可以分解成相量域中直流量的實部與虛部兩部分。由于LC-LC 諧振逆變器濾波效果非常好，可以將其大部分諧波濾除掉，所以這里只考慮基波分量。采用第1 節分析得到由時域向相量域轉化的公式，可以得到實部與虛部分開的量相量域狀態方程，即

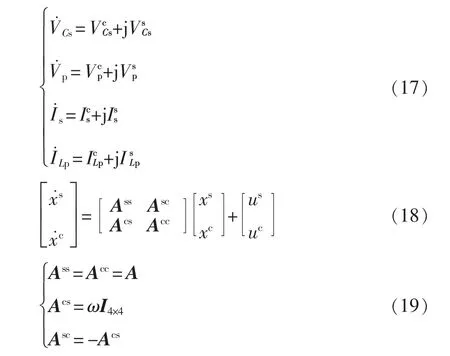
通過時域-相量域的轉化，可以將時域中的時間變量轉化到相量域中，且其實部與虛部均為直流量，因此可以將其線性化。因為變換器的輸入量相比于其開關工作頻率非常低，將式（19）中的微分量置0，用其狀態空間平均模型來表示，即可得到DC/AC 諧振逆變器的各個量在相量域中的穩態解。

全橋LC-LC 串并聯諧振逆變器的相量域大信號模型如圖4 所示，圖中各受控源定義為

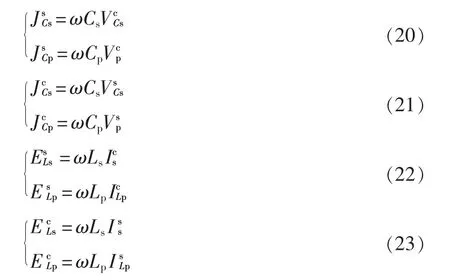
由圖4 可以看出，其結構與圖1 中諧振逆變器的結構相似，只不過每個儲能元件多加入了一個受控源。另外，相量域大信號模型的輸入電壓按照以下方式獲得。令LC-LC 串并聯諧振逆變器的斬波電壓的基波分量va1初始相位為0，由于其初相為0，所以在相量域中，其只含有實部或者虛部中的一個。因此，可以得到逆變橋電壓的基波分量為

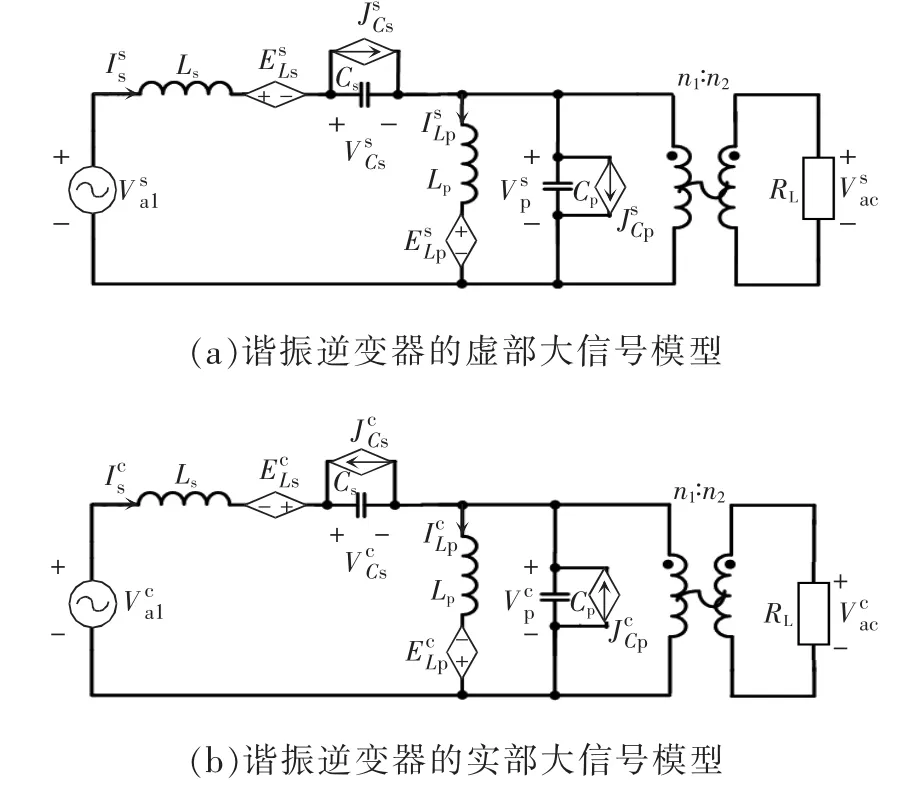
圖4 諧振逆變器大信號模型Fig.4 Large signal model of resonant inverter

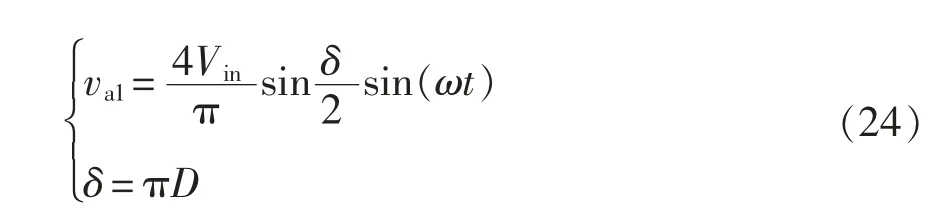
式中：δ 為電壓脈寬；D 為占空比。式（24）在相量域中表示為

因此，可以得出

另外，相量域的電流與電壓分別為

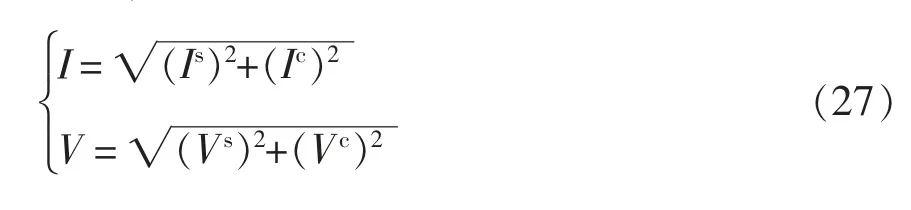
3 全橋LC-LC 諧振逆變器相量域小信號模型

在上述獲得的相量域狀態方程中加入小信號擾動，即可以得到小信號擾動的狀態方程。在本設計中的主要擾動有以下3 種：輸入直流電壓Vdc的擾動、全橋輸出斬波電壓脈寬δ 的擾動、交流母線輸出端高頻交流電流的擾動，其中，交流母線輸出電流擾動又包括幅值擾動和相角擾動。由于本設計采用恒頻移相控制，開關管的驅動角頻率是恒定的，只通過占空比的控制即可實現高頻交流電壓穩定的輸出，所以角頻率ω 為一常數。則擾動量表示為

式中，θ 為輸出高頻電流相對于輸入基波電壓的相位角。

設狀態變量、擾動量和系統的輸出量為

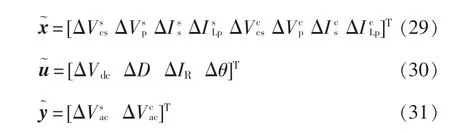
則逆變橋電壓的基波分量實部與虛部分別為

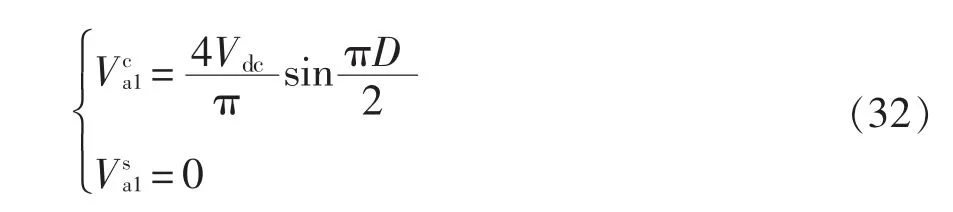
在式（32）中加入小信號擾動，可以得到

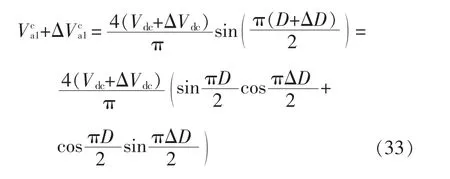
由于擾動信號非常小，通過近似處理可以得到

同時，忽略式（33）中的穩態值和高次項，可以得出

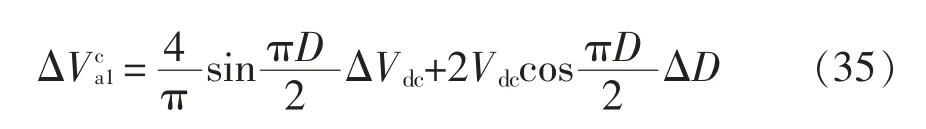
已設θ 后，可得相量域中諧振網絡輸出的電壓為

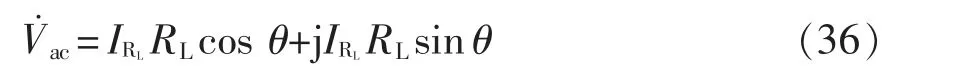
式（36）加入小信號擾動（電流大小和相角擾動），并做一定近似后，可以得到

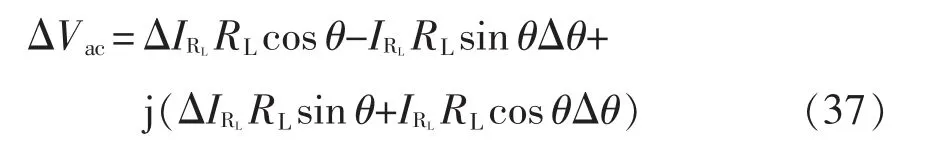
將小信號擾動代入到式（18）中，并忽略等式兩邊的穩態值，即可得到諧振逆變器的小信號模型，則小信號模型的狀態空間關系為

依據式（18）—式（23）可以得出諧振逆變器加入小信號擾動后的等效電路，如圖5 所示。

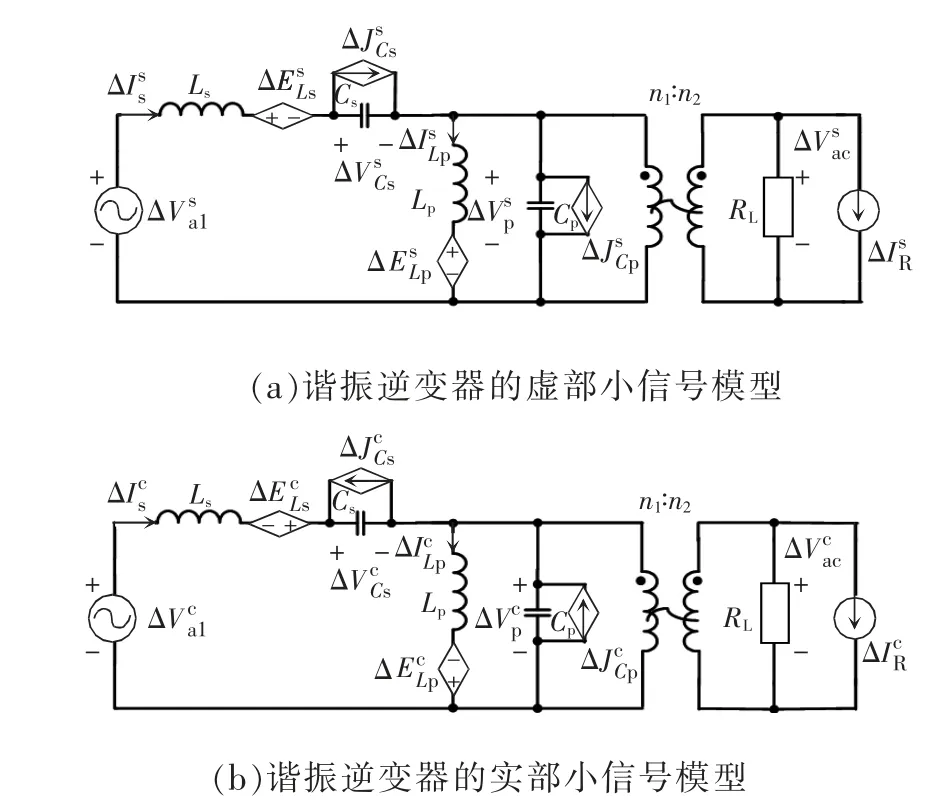
圖5 諧振逆變器的小信號模型Fig.5 Small signal model of resonant inverter

圖5 中，小信號模型的受控源分別定義為

以上對諧振逆變器加入小信號擾動后進行了分析，得出了小信號狀態空間關系式，并得到了諧振逆變器的小信號模型。

將式（38）轉為S 域，即可得到

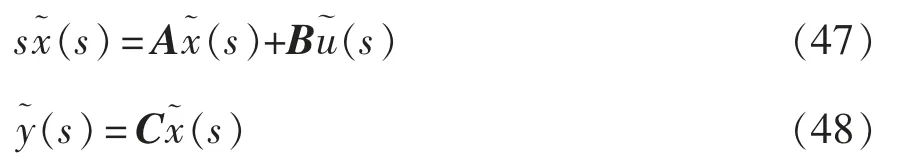
在已知諧振逆變器的各元件參數后，可得逆變器輸出電壓vac相量域小信號模型的傳遞函數為

第1 節對諧振逆變器進行了詳細的分析，由圖2 與圖3 可以得出占空比D 的計算公式為

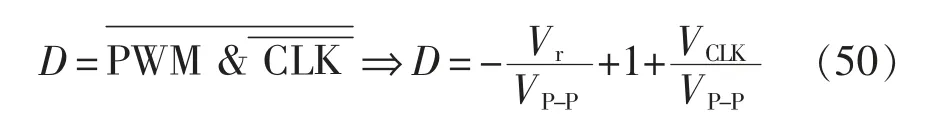
結合已經得出的數據，利用Matlab 軟件可分別計算出相量域中實部與虛部的小信號傳遞函數（s）與（s）。XS、XC是大信號的穩態解，因此從控制端到輸出電壓的小信號傳遞函數可以表示為

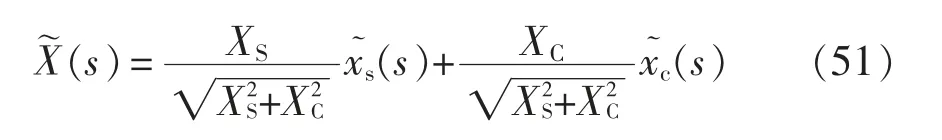
其中，大信號的穩態解XS、XC分別為

4 閉環分析與設計

由圖1 可以看出，如果要實現全橋LC-LC 串并聯諧振逆變器輸出頻率與幅值穩定的高頻交流電壓，必須對其進行閉環控制。閉環反饋控制回路如圖6 所示，其主要包括輸出電壓采集變壓器繞組、二極管全橋整流電路、低通濾波器、直流參考電壓、回路補償器、恒頻移相控制驅動器等。

圖6 閉環反饋控制回路Fig.6 Closed-loop feedback control loop

全橋LC-LC 串并聯諧振逆變器的輸出電壓為高頻交流電壓，通過二極管整流橋整流后可以得到脈動的2 倍于交流電壓頻率的直流電壓，再次經過低通濾波器后即可得到穩定的直流電壓，低通濾波后的直流電壓與給定的直流參考電壓比較后再通過環路補償即可實現逆變器的閉環控制。由于逆變器的濾波網絡包含4 個無源元件，其濾波效果非常好，即非常接近正弦交流電壓，因此，通過整流、低通濾波后得到的直流電壓能很好地反映逆變器輸出高頻交流電壓幅值的變化情況。

本節主要針對閉環回路中的低通濾波器以及系統補償器進行分析與設計。給定參數為：輸入電壓Vdc=（400±28）V，額定輸出功率P=200 W，輸出高頻交流電壓vac頻率f=200 kHz，峰值為Vacm=130 V。串聯電感Ls為590.5 μH，串聯電容Cs為1.189 nF，并聯電感Lp為122 μH，并聯電容Cp為3.608 nF，變壓器T 原邊n1為28 匝，變壓器T 副邊n2為10 匝。

4.1 低通濾波器的設計

由圖1 所示，隔離變壓器共有3 個繞組，其中，原邊繞組n1與副邊繞組n2傳遞能量，繞組n3進行高頻交流電壓的采集。由上述可知，變壓器原邊繞組n1與副邊繞組n2的匝數比為28∶10，本設計中將變壓器原邊n1與副邊n3之比定為28∶1。低通濾波器采用LC 低通濾波器，如圖7 所示，其中忽略了無源元器件的寄生參數。

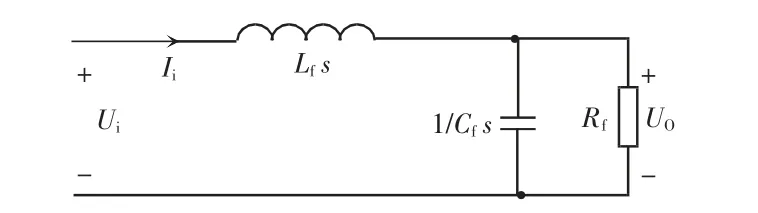
圖7 LC 低通濾波器Fig.7 LC low pass filter

輸出電壓的傳遞函數為

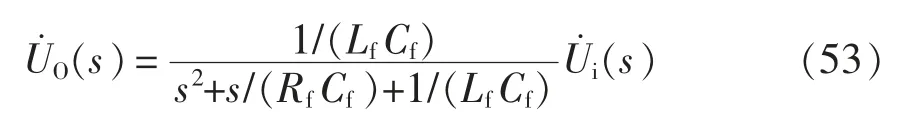
令截止角頻率

阻尼系數

由式（53）可以得出

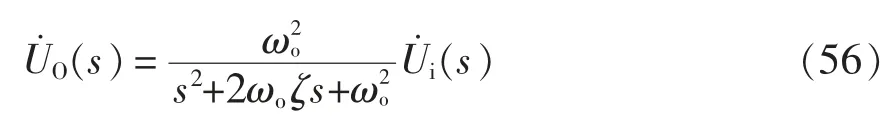
利用Matlab 軟件對LC 低通濾波器在不同截止頻率與阻尼系數下的增益進行分析。圖8 為LC 濾波器在不同截止頻率與不同阻尼系數時不同輸入頻率電壓的增益。由上述已知，二極管整流橋輸出的電壓為2 倍于高頻交流輸出電壓的脈動直流電壓，所以其脈動頻率fD=400 kHz。通過傅里葉分解，除去直流分量，其一次諧波分量的頻率與其脈動頻率相等，因此只須使LC 濾波器濾除輸入電壓一次以及以上的高次諧波即可。

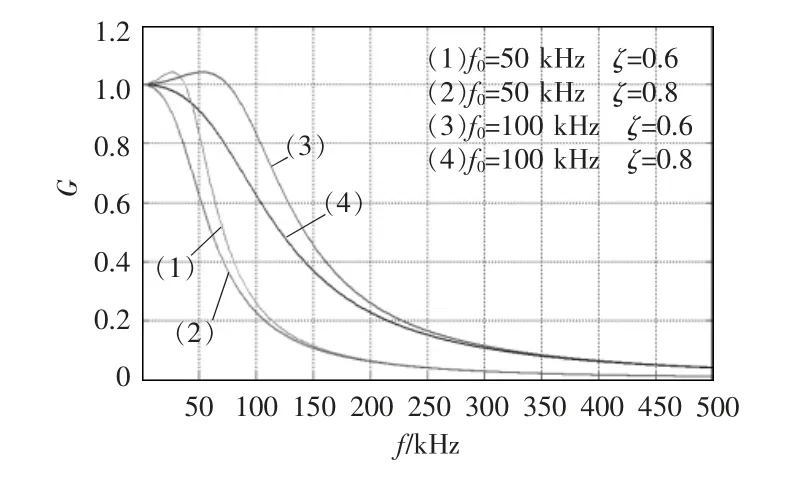
圖8 變壓器原邊電壓增益Fig.8 Voltage gain of the transformer on primary side

由圖8 可以看出，當LC 濾波器截止頻率為f0=100 kHz，阻尼系數為ζ=0.6 時，輸入脈動直流電壓在頻率f=400 kHz 處的增益已經很小，即此時脈動直流電壓中400 kHz 及以上頻率的諧波近似被濾除掉，因此，滿足濾波要求。由此可以計算出濾波器中各個元件的參數，分別為Lf=1.91 mH，Cf=1.5 nF，Rf=1 kΩ。

以上計算出了LC 濾波器的各個元件參數，由于LC 濾波器的輸出電壓為其輸入直流脈動電壓的平均值，所以通過以上已經給定的參數可以計算出LC 濾波器輸出的直流電壓值，即可以反映出高頻交流電壓幅值的大小。通過大電阻分壓，即可以與參考電壓相比較，進而通過補償器與驅動器實現對開關管的移相控制。

4.2 系統補償器的設計

圖9 為加入補償環節的系統原理。利用計算機仿真軟件得出諧振逆變器的小信號傳遞函數后，再加入補償環節即可得到整個系統的傳遞函數（雖然由式（50）給出的占空比D 不是直接利用參考電壓與鋸齒波電壓相比得到的，但其為線性方程，斜率的絕對值不變，所以，為了便于分析，在小信號傳遞模型中用1/VP-P替代）。

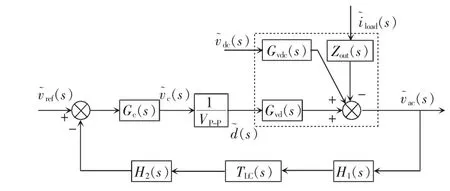
圖9 系統小信號傳遞模型Fig.9 Small signal transfer model of the system

由上述已知，LC-LC 串并聯諧振逆變器中隔離變壓器T 的第二個副邊與第三個副邊之比為n2/n3=10/1，所以，可以得出第一個比例環節為

由第4.1 節可以得出LC 濾波器的傳遞函數為

閉環回路中，設計直流參考電壓Vref=2.5 V，所以在LC 低通濾波器的輸出端還要加入2 個大電阻進行分壓，分壓比為

由諧振逆變器的小信號傳遞模型，可以得到其輸出電壓變量為

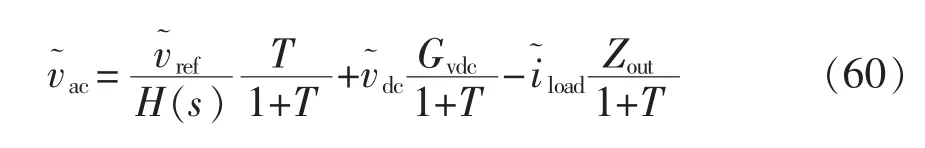
其中，環路增益為

當系統未進行補償時，其補償環節Gc（s）=1，因此可得未補償時的環路增益為

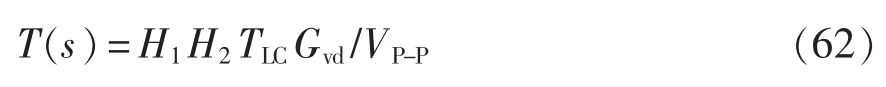
由于諧振逆變器的環路增益與相角裕量會因為諧振逆變器所接的負載不同而發生變化，所以在為諧振逆變器設計補償環路時，要考慮在其最壞情況下進行設計，即應當在諧振變換器處于輸入電壓最大而所接負載為輕載狀態時，對其環路進行補償設計。在本設計中，選擇輸入電壓為最大電壓，即Vdc-max=428 V，選擇負載為50%額定負載，即所接等效負載為RL=84.5 Ω。利用Matlab 仿真軟件可以得出未加補償時傳遞函數的Bode 圖，如圖10 所示。

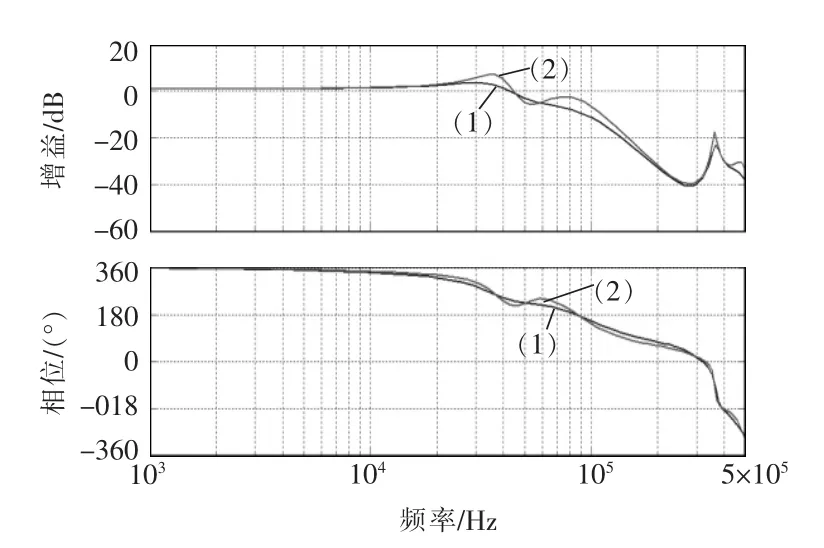
圖10 未加補償時的系統環路Bode 圖Fig.10 Bode diagram of system loop without compensation

由圖10 可以看出，在諧振逆變器輸出端所接為額定負載（1）與50%負載（2）情況下的無補償環路傳遞函數Bode 圖，隨著負載的減小其環路越難穩定，在進行環路補償時只要保證輕載時的系統穩定即可實現整個系統的穩定。所以，以下只針對負載為50%情況下的環路傳遞函數進行補償設計。

本設計將選用傳統的閉環控制方法，至于其他更優的控制閉環控制方式[19-20]在此不再涉及。在反饋系統中，系統傳遞函數的截止頻率越大，則系統抵抗低頻干擾的能力就越強，動態響應越快，系統傳遞函數的截止頻率越大，則抑制高頻干擾的能力就越差，因此一般設計穿越頻率為開關頻率的10%左右。但是，由圖10 所示，由于在頻率f=40 kHz 附近時，系統會出現振蕩現象，振蕩后在頻率40 kHz左右處穿過零點，因此，選擇穿越頻率時應盡量遠離振蕩處。本設計選擇穿越頻率fc=15 kHz，通過觀察圖10 可知，系統的相角裕量比較充足，而低頻增益明顯不夠，所以，本設計利用先加入比例積分，然后再加入實部極點的補償方式對系統進行補償。

比例積分環節的設計方式為，首先選擇比較大的轉折頻率，然后觀察得到的補償后的系統Bode 圖，再設計其增益大小，使其滿足穿越頻率fc=15 kHz。選擇零點轉折頻率fL=40 kHz，可得

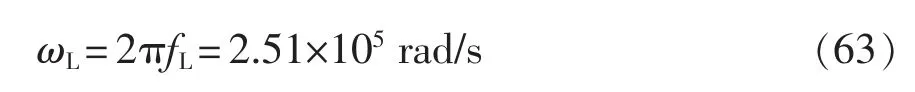
觀察加入積分補償環節后得到的系統Bode圖，若使其穿越零值頻率為fc=15 kHz，則需要加入-10.5 dB 的增益，即需要加入的比例為ki=0.3。

選擇極點頻率fP=18 kHz，可得

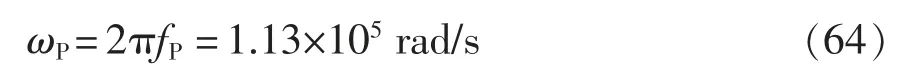
觀察加入極點補償環節后得到的系統Bode圖，在fc=15 kHz 處的增益為-2.24 dB，因此還應加入2.24 dB 的增益，即需要加入的比例為kp=1.3。

由上可以得出所需補償環節的傳遞函數為

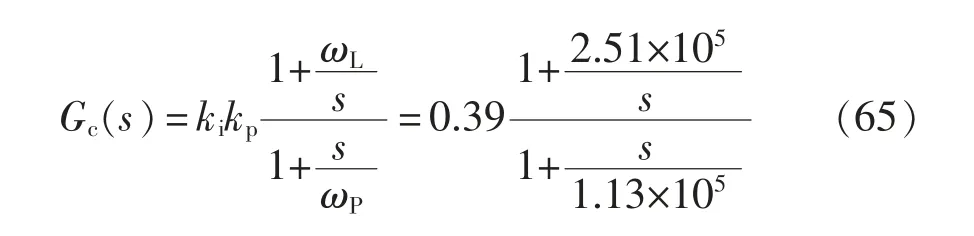
加入補償環節后，可以得出補償后的系統傳遞函數Bode 圖，如圖11 所示。

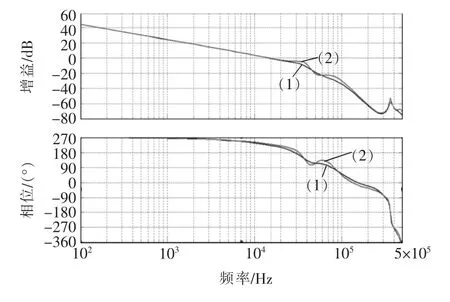
圖11 加入補償環節后系統環路Bode 圖Fig.11 Bode diagram of system loop after adding compensation link

觀察加入補償環節后的全橋LC-LC 串并聯諧振逆變器小信號的Bode 圖，在系統滿載情況下如圖11 中曲線（1）所示，可以看出其在100 Hz 處增益為44 dB，穿越頻率為15 kHz，穿越頻率處的相位裕量為45.3°。在系統帶載50%的情況下，如圖11 中曲線（2）所示，其在100 Hz 處增益為44 dB，穿越頻率為15 kHz，穿越頻率處的相位裕量為52°，因此，系統補償合理。

5 仿真及實驗驗證

5.1 仿真驗證

主電路各個元件的參數與第4 節給出的元件參數相同，為了證明第3 節中全橋LC-LC 串并聯諧振逆變器相量域大信號模型的正確性，利用Matlab軟件進行仿真，可以得出諧振逆變器的開環時域與開環相量域動態仿真對比波形，如圖12 所示。

圖12 逆變器開環時域與相量域動態的仿真對比波形Fig.12 Comparison between time-domain and phasor-domain dynamic simulation waveforms with inverter open-loop

圖12 中，LC-LC 串并聯諧振逆變器在開環最大脈寬狀態下，其直流輸入電壓從0 V 升至200 V 再升至400 V，然后再降至100 V 時的時域與相量域的動態波形。由仿真波形圖可以看出，無論是起始階段，還是在輸入電壓跳變或是穩態階段，相量域的動態仿真波形與時域仿真波形的邊緣非常吻合，也就是說相量域的波形能夠準確地反映出時域電壓與電流幅值的變化，因此，仿真結果證明了采用上述相量建模法建立的全橋LC-LC 串并聯諧振逆變器相量域大信號模型的正確性。

5.2 實驗驗證

為了驗證對全橋LC-LC 串并聯諧振逆變器的小信號建模以及環路補償的正確性，搭建了一臺輸出功率為200 W 的實驗樣機進行測試。實驗樣機的關鍵參數如表1 所示。樣機反饋回路的參數設計依照第4 節中給出的參數進行選取，恒頻移相控制選用UCC3895 芯片，開關管選用電壓自舉芯片IR2110 進行驅動。

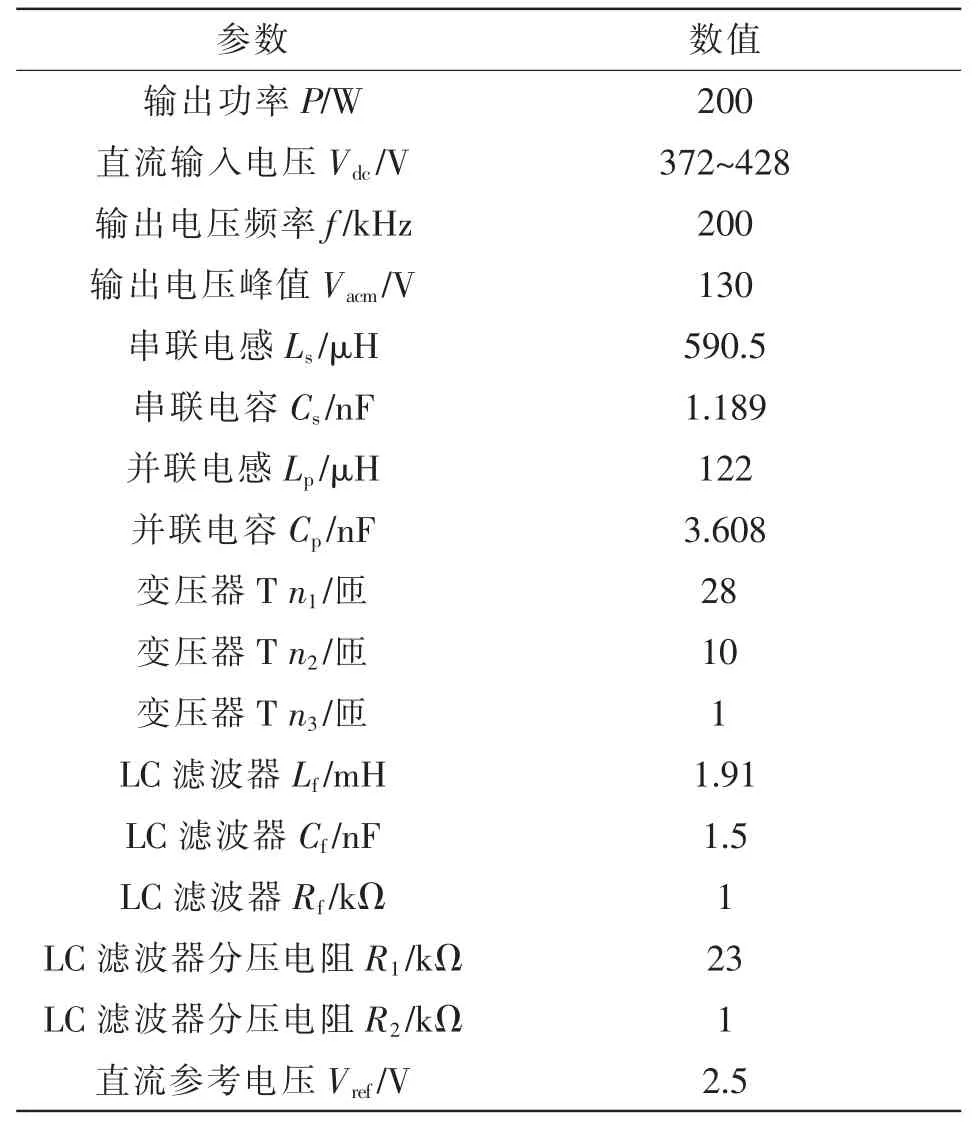
表1 實驗樣機的關鍵參數Tab.1 Key parameters of experimental prototype

圖13 為諧振逆變器開關網絡電壓va、LC-LC 諧振網絡輸入電流is以及逆變器輸出電壓vac的波形，其中輸入直流電壓為400 V。由圖可以看出，諧振網絡的輸入電流is滯后于斬波電壓va，即實現了開關管的軟開通和關斷。而且，輸出高頻交流電壓vac為正弦電壓，其諧波含量非常低，符合規定要求。

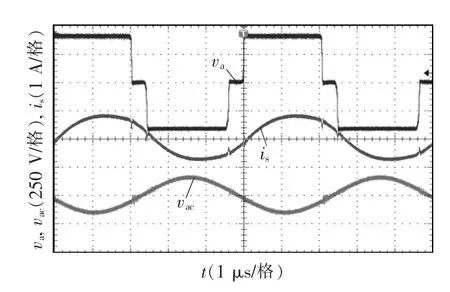
圖13 開關網絡輸出電壓、諧振網絡輸入電流以及逆變器輸出電壓波形Fig.13 Waveforms of output voltage of switch network,input current of resonant network,and output voltage of inverter

圖14 為LC-LC 串并聯諧振逆變器的直流輸入電壓發生變化時，其輸出的高頻交流電壓波形圖。由圖可見，當直流輸入電壓Vdc由360 V 跳變到400 V 與由400 V 跳至360 V 時，輸出電壓vac在短時間內能恢復到原來狀態，由此可見，經過環路補償后，LC-LC 串并聯諧振逆變器能夠很好地抵御電壓波動帶來的影響。

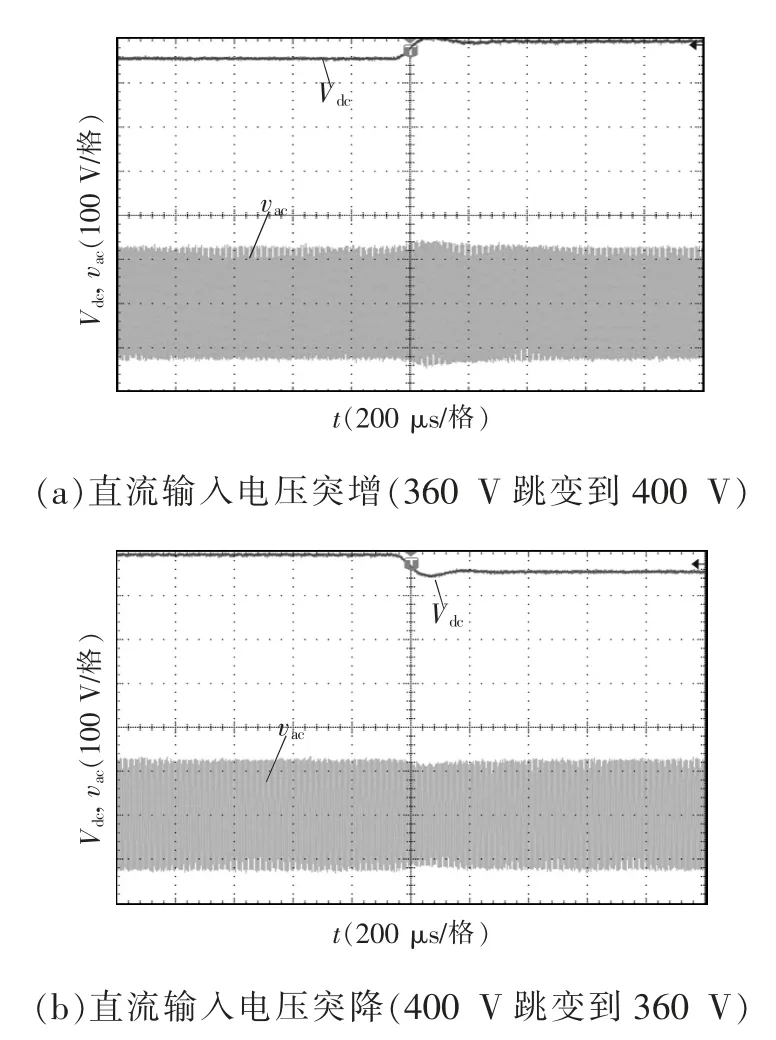
圖14 直流輸入電壓跳變時諧振逆變器的輸出電壓波形Fig.14 Output voltage waveforms of resonant inverter when DC input voltage changes

圖15 為所接負載發生突變時，LC-LC 串并聯諧振逆變器輸出電壓波形圖。由圖可見，當所接負載由滿載跳變到50%負載與由50%負載跳變至滿載時，經過反饋控制的調節，LC-LC 串并聯諧振逆變器的輸出電壓也能夠在短時間內恢復到原來的狀態。經過實驗驗證，諧振逆變器具備了比較好的動態性能，實驗結果很好地驗證了理論分析的正確性。

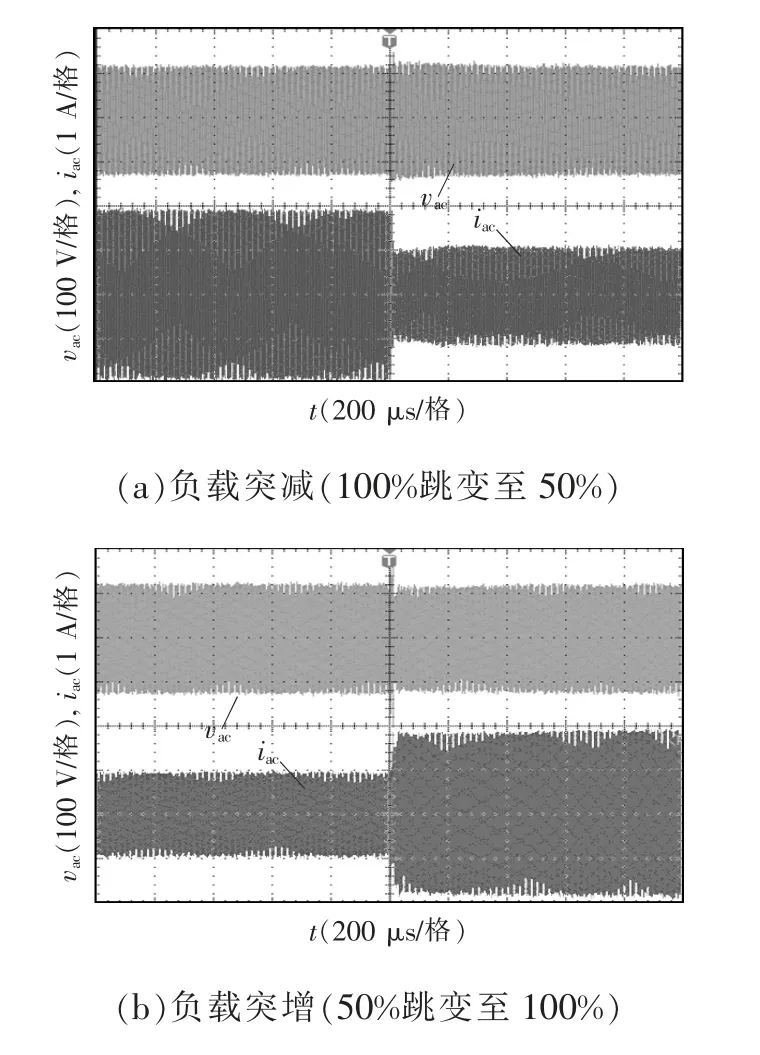
圖15 負載發生突變時諧振逆變器輸出電壓波形Fig.15 Output voltage waveforms of resonant inverter when load changes

6 結語

本文采用相量建模法建立其相量域的大信號模型，進而建立其小信號模型，根據所建立的恒頻移相控制全橋LC-LC 串并聯諧振逆變器小信號模型，進行了環路補償設計。最后，搭建了功率為200 W 的實驗樣機，進行了相關實驗驗證，仿真結果表明了采用上述相量建模法建立的全橋LC-LC串并聯諧振逆變器相量域大信號模型的正確性。同時，實驗結果表明，經過閉環控制，諧振逆變器具有良好的抗輸入電壓和負載變化擾動的能力，達到了預期的效果。