基于磁通量法索力測量模型參數的調適研究*

劉小鋒，馮志敏，胡海剛，馮少玉，徐俊峰

(寧波大學海運學院，浙江 寧波 315832)

橋梁作為海洋工程中一項基礎設施，對促進我國經濟發展、便利人們生活方面發揮著十分積極的作用。拉索橋是當前較為常見的橋型，其中，拉索作為其主要承載構件，索力直接控制著整橋內力分布與線形。在橋梁長期運營過程中，重復變化的動載荷又將使拉索產生疲勞損傷，極大地威脅著橋梁的安全性與穩定性[1-3]，因此精確測量索力可為橋梁運營維護管理提供有力的參考依據。

目前，索力測量的方法主要有油壓表法、壓力傳感器法、振動頻率法和磁通量法等，相比于其他幾種方法，磁通量法具有精度高、動態性好、壽命長、可實現全天候測量等諸多優點[4-7]，現已得到廣泛地應用和研究。龍躍[8]、鄧年春[9]、Zhao Y[10]、何利[11]、殷鵬雷[12]、Cho S[13]等分別利用磁通量傳感器對天津永和大橋、湛江海灣大橋、香港昂船洲大橋、宜賓長江大橋、臺州椒江二橋、韓國Hwamyung大橋進行索力監測，測量精度平均在3%左右。磁通量傳感器在使用前需預先標定，以獲得索力與感應電壓間的模型關系。標定時，通常只對拉索進行單次逐級加載，以得到標定樣本。然而，拉索卸載后，再次對其逐級張拉，獲得的標定樣本會與第1次標定樣本間存有差異[14]，故單次標定模型精度穩定性較低。為此，徐聰[15]、任亮[16]、Cappello C[17]對試件進行3次循環加載，并取標定樣本均值擬合模型，在一定程度上提高了模型精度的穩定性。雖然平均標定法運算簡單，但卻不能充分利用每組標定樣本信息，造成了一定的信息資源浪費；此外，平均標定法的模型參數在實際索力測量時保持固定不變，故難以保證標定模型對每次隨機測量均能達到較高精度。因此，對拉索進行多次加載標定，并充分挖掘每組標定樣本信息，使模型參數隨每次測量能夠被適應性地調整，將對進一步提高索力測量精度及穩定性具有重要意義。

本文提出模型參數調適方法，分別對各組標定樣本線性擬合，基于交叉測試和最近距離分配方法，使得實測感應電壓可自適應地選擇模型參數計算索力，每組標定樣本信息都得到了充分利用。室溫18℃時，在試驗機上對15.2 mm鋼絞線多次加載，并利用磁通量傳感器測量對應感應電壓，共獲得4組標定樣本和15個隨機測試樣本。基于獲得的實驗數據，對單次標定、平均標定和模型參數調適法進行測試、對比和分析，驗證了模型參數調適法具有更高的測量精度及穩定性。

1 磁通量法索力測量原理

當鐵磁材料在受到外力作用時，內部磁特性(如磁導率)將發生改變，此稱為鐵磁材料的磁彈效應[18]。拉索一般是由多根預應力鋼絞線組成，屬于鐵磁材質，磁通量法正是基于拉索的磁彈效應利用磁通量傳感器來測量索力。安裝于拉索上的磁通量傳感器一般為套筒式，其主要由勵磁線圈、感應線圈、對應線圈骨架、外殼等組成，結構如圖1所示。

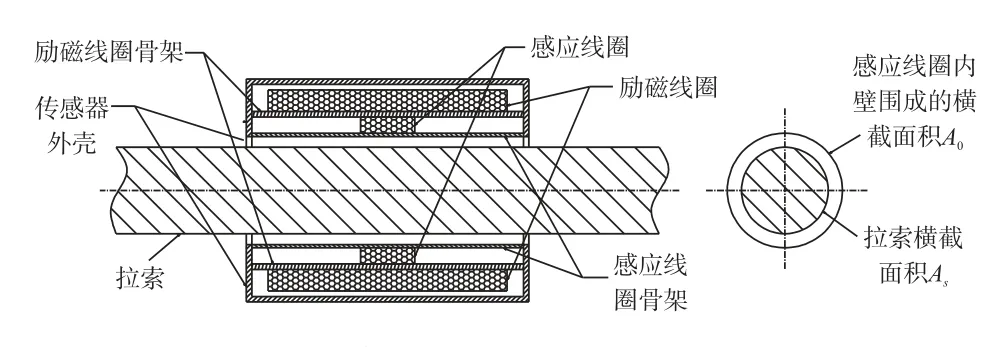
圖1 套筒式磁通量傳感器結構

磁通量傳感器工作時，勵磁線圈以一定頻率對拉索進行勵磁，感應線圈產生相應的感應電壓。其中，感應電壓大小取決于單位時間內通過感應線圈的磁通量，而磁通量又與線圈鐵芯的磁導率有關。拉索作為線圈鐵芯，其磁導率計算公式為[19]:

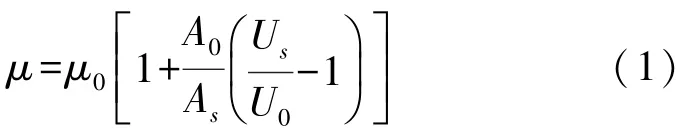
式中:μ為拉索磁導率、μ0為真空磁導率、As為拉索橫截面積、A0為感應線圈內壁橫截面積、Us為感應線圈中含拉索時的感應電壓、U0為感應線圈中不含拉索時的感應電壓。

當拉索受到軸向拉力時，磁導率將發生變化，由式(1)可得:

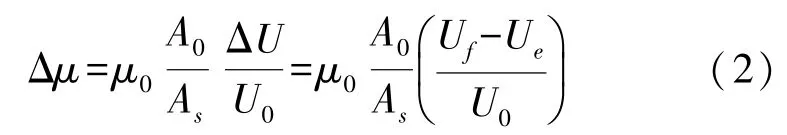
式中:Δμ為拉索磁導率變化量、Uf為拉索承載時的感應電壓、Ue為拉索空載時的感應電壓。

根據Joule效應，得拉索軸向應變與磁導率變化量間的關系為[20]:

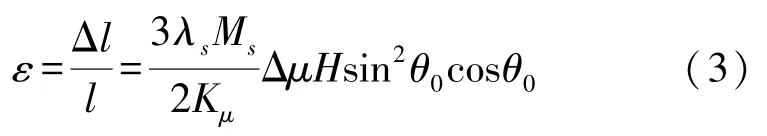
式中:ε為拉索軸向應變、l為拉索長度、Δl為拉索軸向伸長量、λs為軸向變形常數、Ms為飽和磁化強度、H為外磁場強度、Kμ為單軸磁各項異性常數、θ0為磁場與易磁化軸間角度。

再由應力應變間關系得:

式中:σ為拉索橫截面應力、E為拉索材料的彈性模量、F為索力。

聯立式(2)~式(4)，得索力與感應電壓間的關系為:

由式(5)可知，F與Uf間具有線性關系，斜率和截距參數通過標定獲得。

2 模型參數調適法

為充分挖掘多組標定樣本信息，并使標定出的模型參數隨實測感應電壓作適應調整，提出了模型參數調適法。該方法首先利用最小二乘法對各組標定樣本線性擬合，確定各模型參數，再對各擬合模型采用其他組標定樣本交叉測試，從而獲得各模型參數下每級測試誤差均值，然后根據實測感應電壓與各組標定樣本同級感應電壓距離之和，找出最小距離對應級次以及該級次下交叉測試時最小誤差均值對應模型參數，最后將實測感應電壓代入此參數下模型計算索力。模型參數調適法的具體步驟如下:

①令第i組標定、第j級加載獲得的感應電壓與索力樣本為(Uij，Fij)，i＝1，2，…，m；j＝1，2，…，n。其中，m為標定組數、n為加載級數。

②基于最小二乘法，線性擬合第i(i＝1，2，…，m)組標定樣本集{(Uij，Fij)，j＝1，2，…，n}元素，確定模型參數ki、bi，得索力與感應電壓間第i個標定模型為:

③將第c(c≠i，c＝1，2，…，m)組標定樣本集{(Ucj，Fcj)，j＝1，2，…，n}中的Ucj代入式(6)中的U，得相應測試索力為:

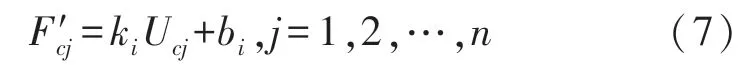
④計算集合{F′cj，j＝1，2，…，n}中各元素相對誤差為:

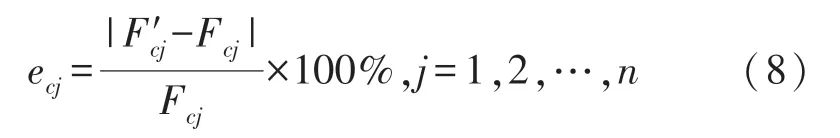
⑤計算除第i組標定樣本各級的測試索力平均相對誤差為:

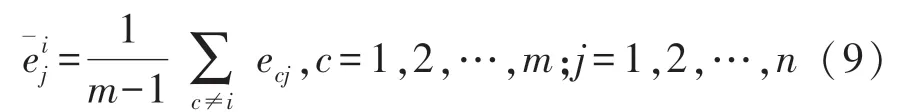
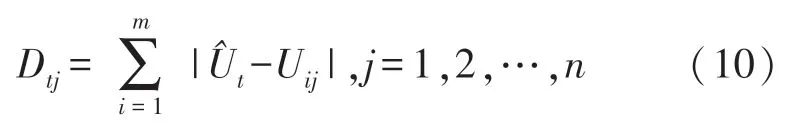
⑦找出集合{Dtj，j＝1，2，…，n}中最小值元素對應的指標j，取步驟5中j值下各模型的，得集合，i＝1，2，…，m}。

模型參數調適法流程如圖2所示。

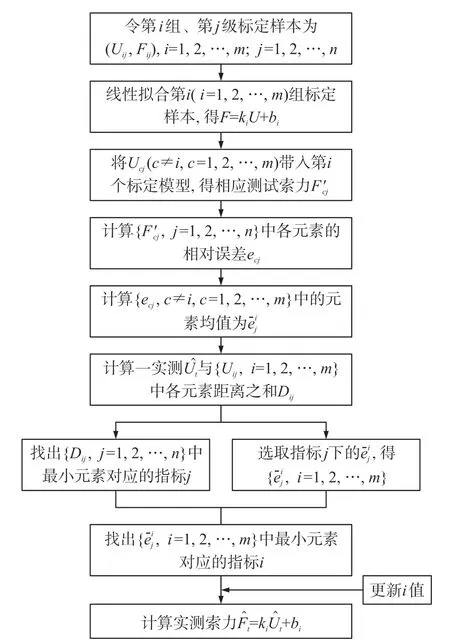
圖2 模型參數調適法流程圖

由此可知，模型參數調適法利用標定樣本對各模型交叉測試時的最小誤差均值來確定每級最優模型參數，并基于聚類思想，以實測感應電壓與標定感應電壓最近距離對應級次來分配模型參數，故當標定樣本選取的足夠均勻合理時，該方法將對實際工程中索力測量精度提高十分有益。

3 實驗與分析

3.1 實驗方法

將磁通量傳感器安裝固定到一段鋼絞線上，再將鋼絞線兩端安裝于試驗機上下夾頭中。在室內某溫度下，利用試驗機以一定步長對鋼絞線逐級加載至設定值，同時利用磁通量傳感器測量出鋼絞線在各級加載下的感應電壓，按此過程循環測量多次，獲得多組標定樣本，并將它們取均值，作為新的一組標定樣本。再對鋼絞線隨機加載，獲得多個測試樣本。根據獲得的實驗數據，分別對單次標定、平均標定、模型參數調適法進行測試，通過對比分析測試結果，驗證模型參數調適法的可行性和有效性。

3.2 實驗條件及數據獲取

實驗選用鋼絞線長度為700 mm、直徑為15.2 mm，磁通量傳感器由深圳某公司生產，內徑為17 mm、外徑為45 mm、長度為210 mm，試驗機由長春機械科學研究院有限公司生產，最大拉力為100 kN，實驗系統如圖3所示。在室內溫度18℃下，利用試驗機以2 kN為步長對鋼絞線從0 kN逐級加載至30 kN，同時利用磁通量傳感器測量各級加載下的感應電壓，按此過程循環3次，共獲得3組標定樣本，再取3組標定樣本的均值作為第4組標定樣本，各組標定樣本如表1所示。再對鋼絞線進行15次隨機加載測量，共獲得15個測試樣本，如表2所示。

圖3 磁通量法索力測量實驗系統

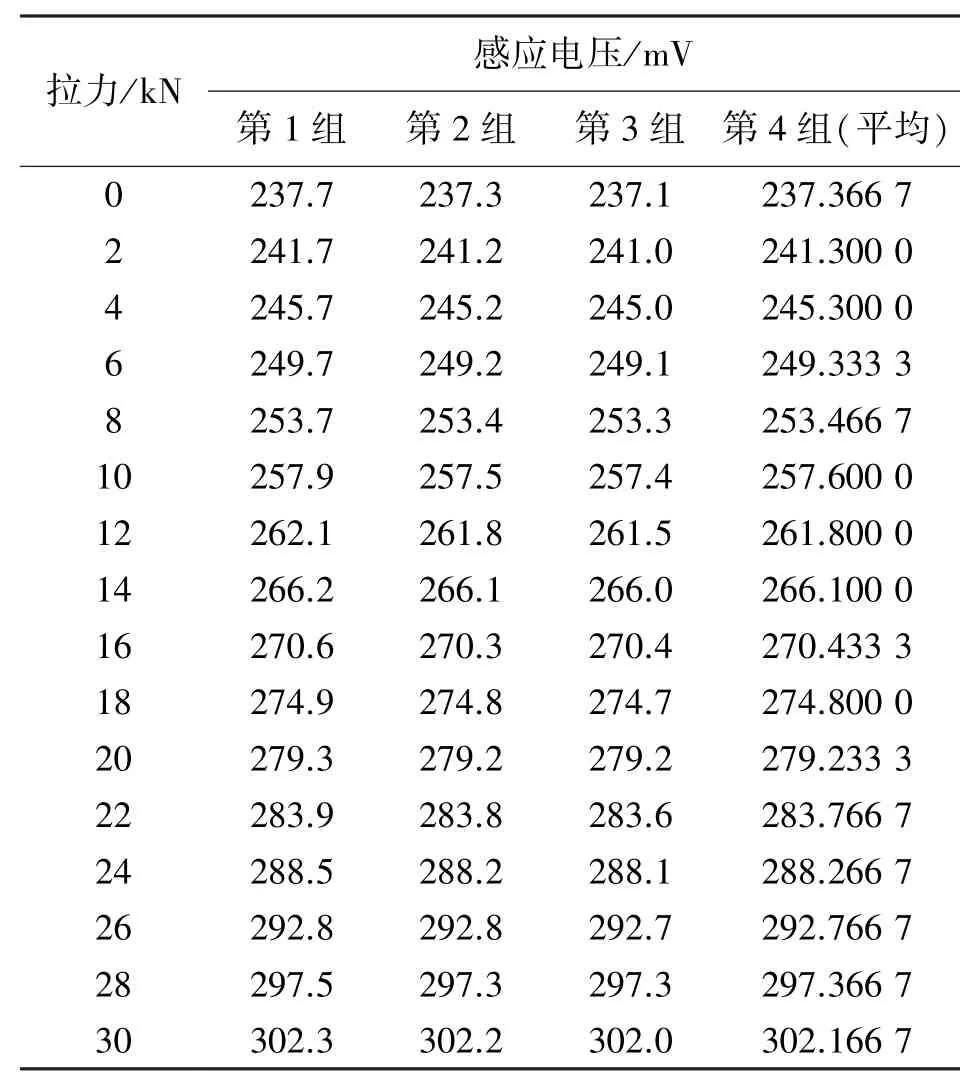
表1 標定樣本數據

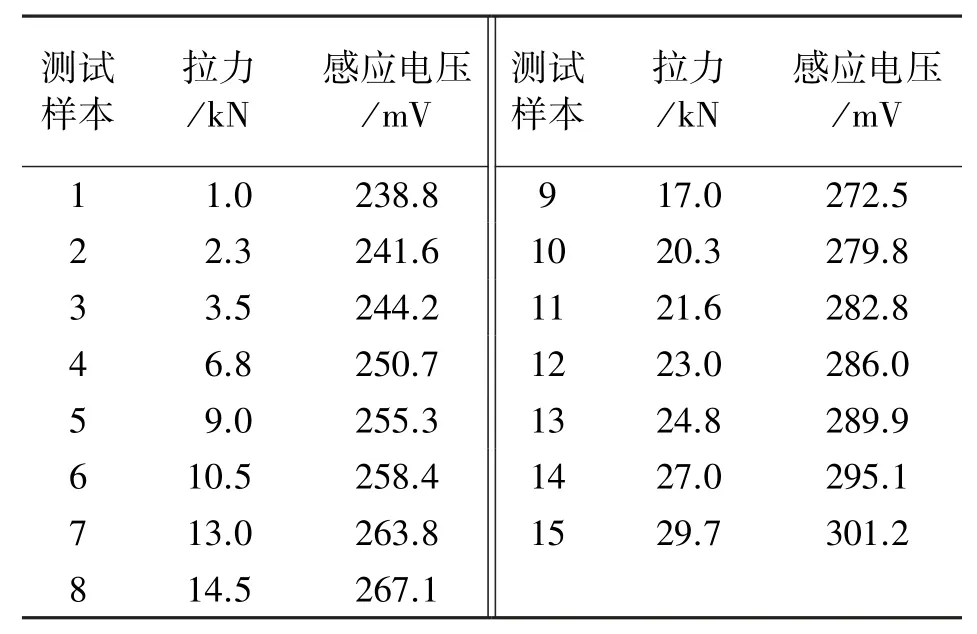
表2 測試樣本數據

3.3 測試結果及分析

利用最小二乘法分別對4組標定樣本線性擬合，結果如圖4所示。從圖中可看出，各擬合線均能很好地通過樣本點，相關系數也都在0.999 6以上，說明拉力與感應電壓間具有高度的線性正相關關系，符合磁通量法測量理論，同時也表明磁通量傳感器工作正常。4個線性模型的斜率k和截距b如表3所示。表中可知，各模型參數間均有差異，故對應的拉力測量結果也必將不同。

表3 四個線性模型參數值

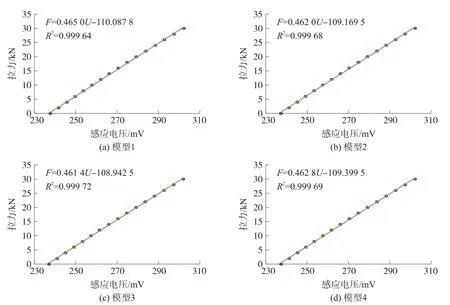
圖4 四個線性模型

利用上述4個模型對15個測試樣本進行測量，對應的測量誤差如圖5所示。由圖5可知，各模型測量誤差不同，在一些測試樣本處還存有較大差異，且各模型精度隨測試樣本不同而變化，表明單次標定模型的精度穩定性較差；此外，模型4雖具有稍好的精度穩定性，但對每個測試樣本并不具有最高測量精度，即若直接利用平均標定法來獲得最終測量模型，必將導致精度較高的其他模型被棄用。因此，對于每個測試樣本，應選擇合適的模型參數，以獲得較平均標定法更高的測量精度及穩定性。

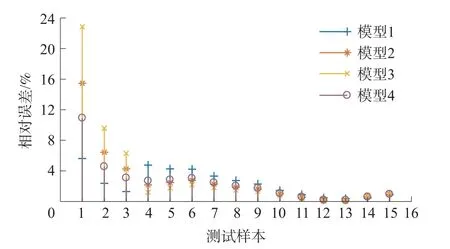
圖5 四個模型的測量誤差

利用模型參數調適法對15個測試樣本測量，其中每個測試樣本所選取的模型參數如表4所示。表中可知，模型參數調適法的模型參數隨測試樣本動態變化，表明模型參數調適法可根據實測感應電壓來對模型參數進行適應性選擇。

表4 測試樣本模型參數選擇表

將模型參數調適法與平均標定法的測量結果及誤差進行對比，結果如表5所示。表中可知，模型參數調適法的測量誤差都低于平均標定法，表明模型參數調適法對提高測量精度取得了顯著效果；此外，經表中計算可得，模型參數調適法與平均標定法測試誤差的均值分別為1.507 5%和2.469 0%，表明模型參數調適法的精度比平均標定法提高了1.6378倍；模型參數調適法與平均標定法測試誤差的標準差分別為1.371 1和2.661 5，表明模型參數調適法的精度穩定性比平均標定法提高了1.941 1倍。

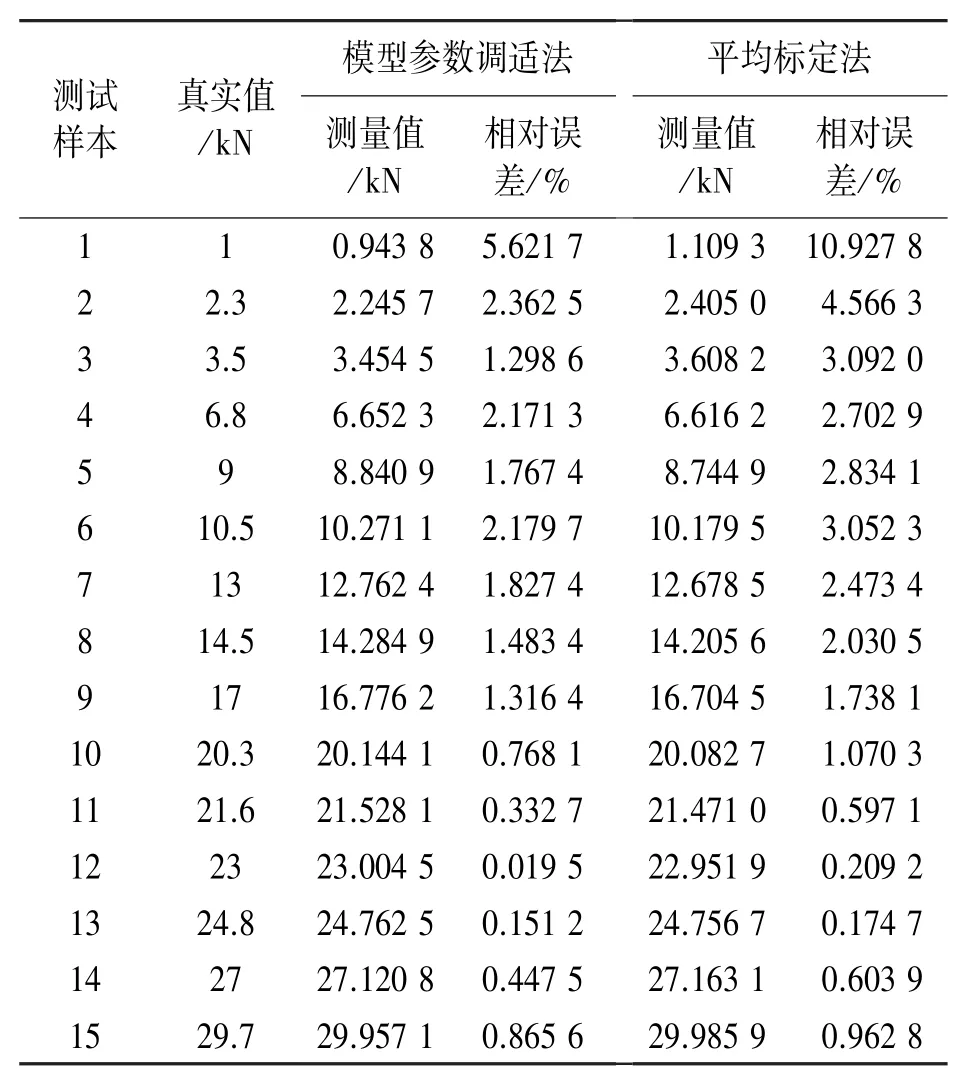
表5 模型參數調適法和平均標定法的測量結果及誤差對比

綜上所述，由于各單次標定模型參數不同，使得一些測量誤差存有較大差異，平均標定法雖綜合了每次標定樣本信息，獲得稍好的精度穩定性，但因對信息利用率較低，精度并沒有達到最高，而模型參數調適法可根據每次實測感應電壓適應性地選擇合理的模型參數，使每組標定樣本信息均得到充分利用，相應地減小了測量誤差，從而較平均標定法提高了測量精度和穩定性。

4 結論

本文提出了模型參數調適法，通過在試驗機上對15.2mm鋼絞線多級加載，并利用磁通量傳感器測量鋼絞線各級加載下的感應電壓，得到18℃下4組標定樣本和15個隨機測試樣本。根據獲得的實驗數據，對單次標定、平均標定、模型參數調適法進行測試，通過對比分析，得出以下結論:

①各單次標定模型參數不同，在一些測試樣本處測量誤差還存有較大差異，故有必要對模型參數進行多次標定，從而通過有效利用標定樣本信息，以提高測量精度及穩定性。

②平均標定法較單次標定法具有稍好的精度穩定性，測量誤差的均值和標準差分別為2.469 0%、2.661 5，但對標定樣本信息利用率低，測量精度和穩定性有待進一步提高。

③模型參數調適法對標定樣本信息利用率高，在測量時模型參數可隨實測感應電壓自動調整，測量誤差的均值和標準差分別為1.507 5%、1.371 1，測量精度和穩定性較平均標定法分別提高了1.637 8倍和1.941 1倍。模型參數調適法將對拉索橋索力測量精度及穩定性的提高具有重要作用。