基于NSGA-II和SVDD的轉向架構架異常狀態監測*

李 鵬，黃培煒，丁 瀛，杜藝博，彭嘉潮

(華東交通大學機電與車輛工程學院，江西 南昌 330013)

轉向架構架是列車的關鍵承載部件，具有傳遞列車主要載荷、固定車軸位置的作用，其健康狀態極大地影響了列車運行安全。2017年12月，日本新干線“希望34號”列車轉向架出現14cm長裂紋，被定為“嚴重”事故。近年來，針對轉向架構架的狀態監測研究已得到了廣泛的關注[1-3]。高云霄等人通過分析構架關鍵測點動應力和載荷應力的傳遞關系，實現了構架側滾、蛇形失穩和扭轉等狀態的識別，一定程度上彌補了測力構架法成本高昂過程復雜的不足[4]。張楠等人通過基于頻率響應函數的傳感器分布優化方法，探索了利用有限數量傳感器獲取有效轉向架構架振動信息的方法[5]。Jun-Sung Goo等研究城市列車行駛時由道碴飛揚現象引起的玻璃纖維增強樹脂基復合材料轉向架結構完整性問題，研究通過獲取復合材料轉向架在飛碴沖擊下的殘余應力和應變信息，對損傷后的復合轉向架構架進行靜力分析并評價結構完整性[6]。

目前，構架狀態監測建模中面臨的異常狀態復雜多樣性，以及監測中傳感器的分布優化問題已引起了廣泛的重視。而各種傳感器分布優化方法其主要區別是在優化目標函數和優化算法的選擇上[7-9]，優化目標函數和優化算法的選取對傳感器分布優化結果的有效性及計算的復雜性具有重大影響。因此，如何定義優化目標函數，并通過布置更少的傳感器，獲取更多的結構有效響應數據和特征，對于工程應用具有重要意義。

研究針對構架異常狀態下樣本集的隨機多樣和不確定性，引入支持向量數據描述(support vector data description，SVDD)算法，以構架正常狀態的樣本集構建SVDD超球體模型對多工況條件下構架的異常狀態進行識別。同時基于改進的非劣分層多目標遺傳算法(non-dominated sorting genetic algorithm II，NSGA-II)對傳感器分布進行了優化[10]。

1 狀態監測對象

研究以209型轉向架構架為對象，旨在通過傳感器分布優化，實現對構架健康狀態的有效監測。研究基于相似原理[11]，采用相同的材料(Q235A鋼)，按5:1尺寸比制備構架結構模型，如圖1所示。

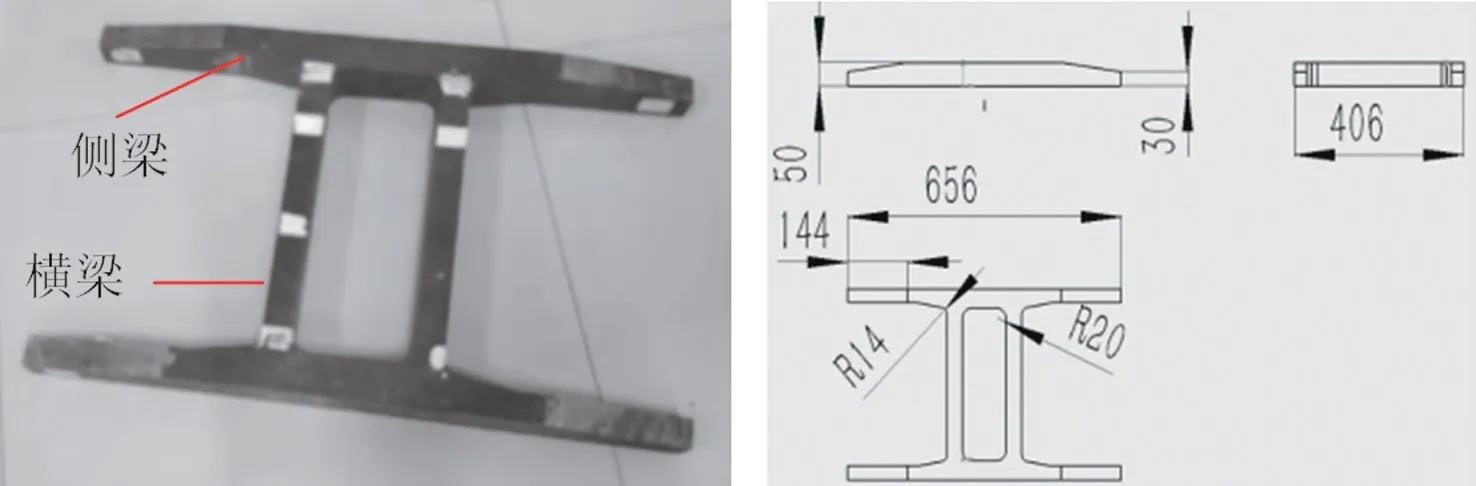
圖1 構架結構模型

209P型轉向架用于客車或貨車居多，在實際運行中，25G型客車上的轉向架構架發生異常率較高與其他車型。當客車車體平穩經過鐵軌，轉向架及其構架在相對穩定下運行，轉向架構架主要受靜載荷的影響產生形變。如圖2(a)所示，209型客車轉向架構架通過搖枕與車體相連接，承受車體的重力。輪對通過導柱支撐板與構架銜接，對構架提供支撐力。構架所受載荷如圖2(b)所示，F1a、F1b、F2a、F2b對應導柱支撐板提供的支持力；A、B、C、D點上FA、FB、FC、FD對應車體通過搖枕施加在構架上的車體重力。

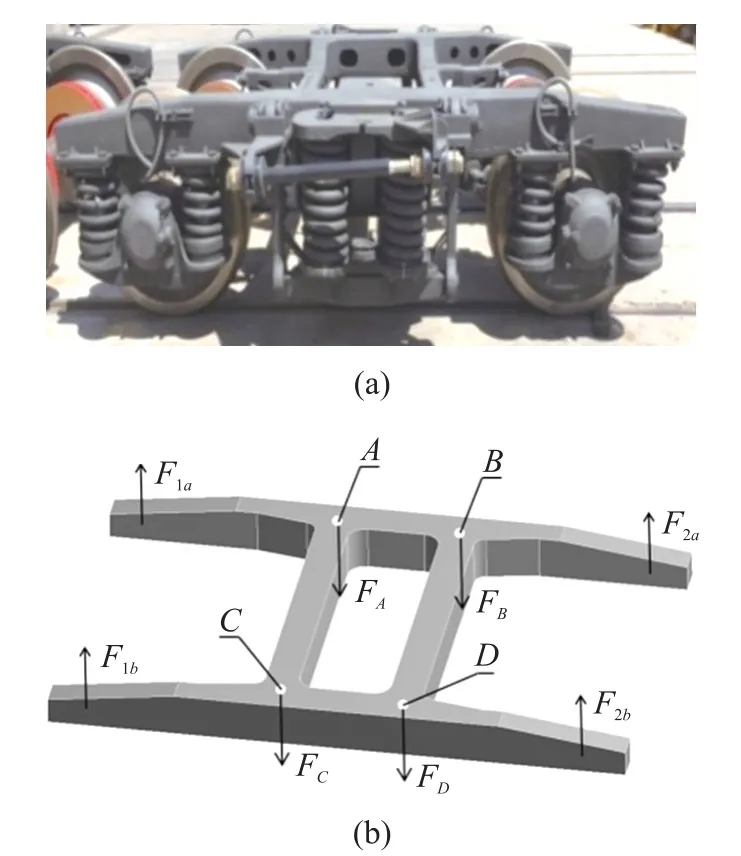
圖2 構架結構模型所受載荷圖

由于構架主要承受垂直方向上的力，因此將構架水平方向表面作為傳感器布置面，傳感器備選點應盡可能覆蓋整個構架，同時結合實際工程經驗，同類轉向架構架常見裂紋部位主要集中在構架端梁彎角處、構架上各吊座焊接處以及橫梁兩端與側梁結合的彎角處[12]。如圖3所示，在構架上均勻分布的14個傳感器備選點，用于安裝傳感器獲取應變響應。

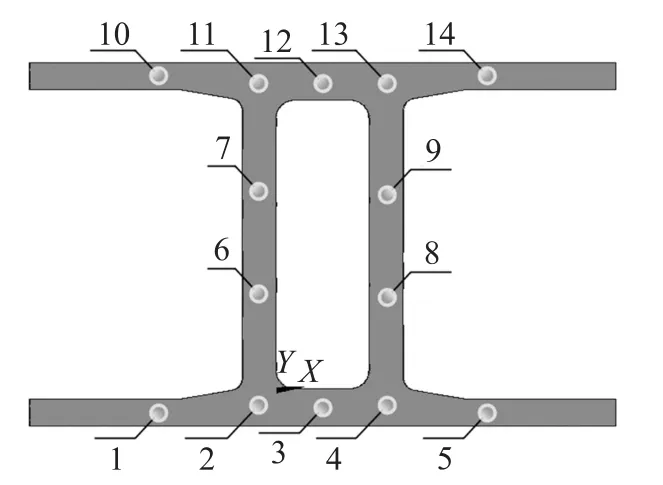
圖3 傳感器備選點編號

2 優化目標

傳感器分布優化的目標是通過優化傳感器的位置，以較少數量的傳感器實現對構架健康狀態的有效監測，研究據此設計雙目標優化函數f1和f2。

2.1 目標函數f1:傳感器數量

目標函數f1—傳感器數量是指布置于構架上的傳感器個數，有效地減少傳感器數量，不僅可以降低監測系統的成本，而且有利于加快數據的處理速度，提高監測系統的實時性[13]。

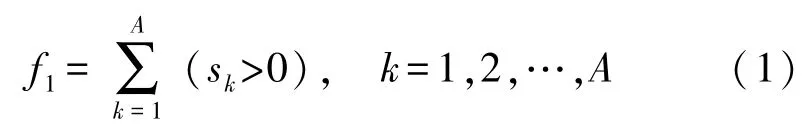
2.2 目標函數f2:超球體聚類指標最大化

支持向量數據描述算法提供了一種采用超球體進行樣本集邊界定義的方法[14]。研究考慮到構架異常狀態下樣本集的隨機多樣和不確定性，期望通過優化正常狀態樣本識別正確率B獲得能有效包含構架正常狀態樣本集的超球體最小半徑，進而定義目標函數f2。

SVDD算法通過內核函數使樣本集周圍形成超球體邊界[15]，其結構誤差ε定義為:

對于SVDD構建的超球體而言，好的超球體邊界描述應包括所有目標樣本，但不包括多余的空間。由此可得到最小化約束條件:

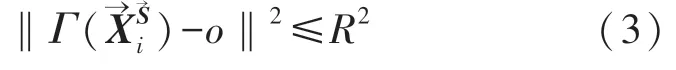
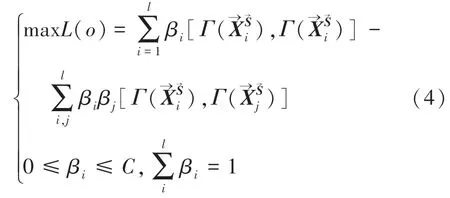
由式(4)可求出超球體中心o的最優解:

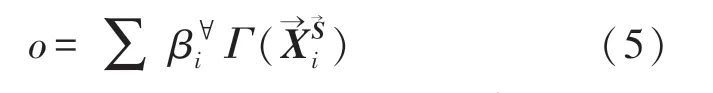
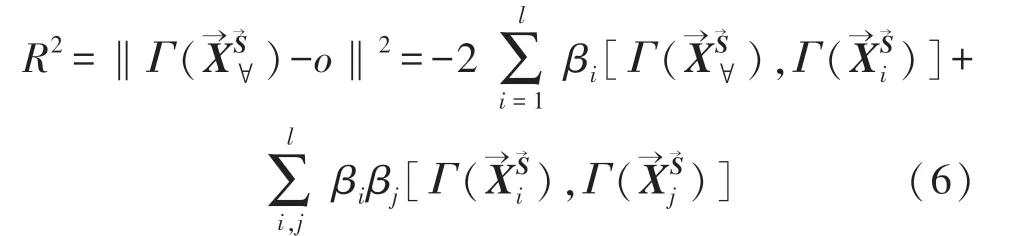
對于新樣本→Y→S:

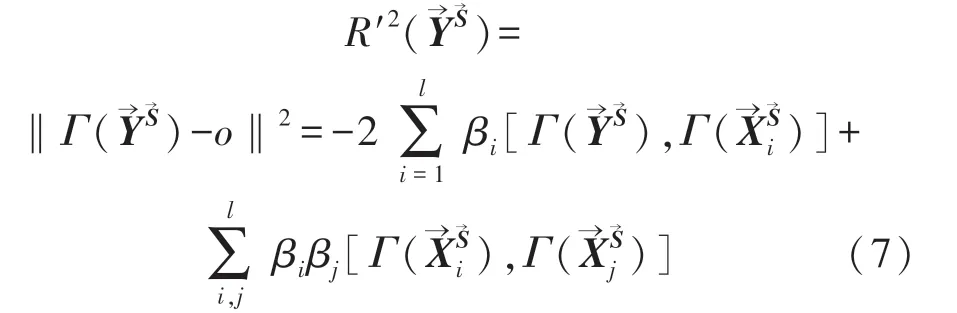
假設構架在p種工況的正常狀態下的樣本數為p×a，a為構架每個工況下的正常狀態的樣本數。在a中隨機取b個用于SVDD建模，其余作為評價樣本，用于量化目標函數f2，同時以特征維數m為權值，則目標函數f2可表示為:

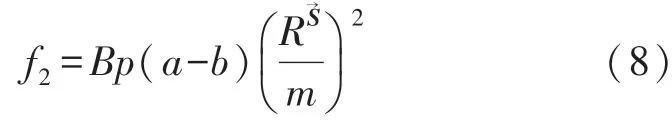
3 非劣分層遺傳算法優化

研究中傳感器分布優化目標函數包括f1—傳感器數量和目標函數f2—超球體聚類指標，屬于雙目標優化問題，兩個目標函數在優化過程中相互沖突和影響，存在優化方向非一致問題，即隨著f1的增大，f2也會增加無法獲得最優解。因此，研究引入非劣分層思想，基于遺傳算法獲取滿足優化目標的傳感器分布非劣解集[17]。

NSGA-II是一種基于最優保存策略的隨機尋優算法[18]，其本質是模擬自然中生物進化的過程，遵循物競天擇的原則，個體優勢基因將有更大機會傳遞下去，同時加入一定的變異概率，從而可以避免陷入局部最優解，找到全局最優解。具體步驟如下:

步驟1 設定個體編碼方式

傳感器分布方案采用A維列向量→S表示，→S中元素Sk取值1(或0)表示第k個待優化傳感器備選點有(或無)傳感器。圖4為一種傳感器分布方案的編碼，表示在傳感器4和7號備選點放置有傳感器。

圖4 傳感器分布方案編碼

步驟2 設定優化參數

設定迭代次數T，交叉概率pc，變異概率pm。

步驟3 創建初始種群

隨機生成規模為n的初始種群:

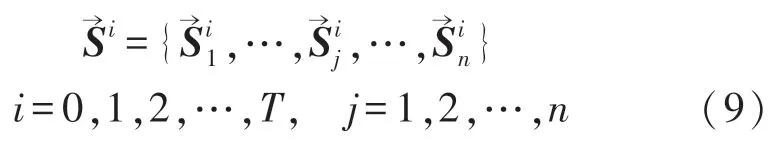
式中:i為0時表示初始種群，T為迭代終止次數，j表示種群中個體的編號。

步驟3 建立優選池

由式(1)和式(8)計算種群中所有個體的目標函數f1和目標函數f2的值，據此對所有個體進行非劣層級劃分，并采用輪盤賭從父代中挑選n個個體放入優選池Mi′。

步驟4 生成交叉種群

每次隨機從Mi′中選擇2個個體，按隨機生成的交叉點對兩個個體進行交叉操作，交叉種群Mi″規模為n×pc。

步驟5 生成變異種群

每次隨機從Mi′中選擇1個個體，按隨機生成的變異點對該個體進行變異操作，變異種群Mi″規模為n×pm。

步驟6 生成子代

將優選池、交叉種群和變異種群合并，并根據目標函數f1和目標函數f2的值對合并后的種群進行非劣層級劃分，將非劣層級最前和擁擠距離最大的n個個體放入子代Si＋1。

步驟7 迭代終止條件

①將Si＋1同Si第一非劣層級中的個體進行比較，出現連續100次迭代結果相同時，則迭代結束；

②迭代次數達到10 000次，迭代結束。

4 實驗驗證

4.1 多工況下構架正常狀態樣本集采集

對于一節客車車體而言，209P型轉向架的技術參數如表1:

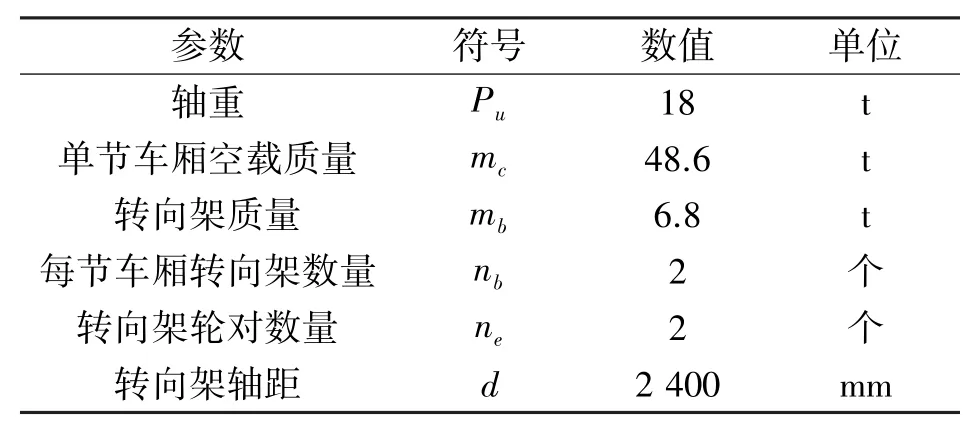
表1 209P型轉向架基本參數

研究采用其一節車廂空載時質量mc＝48.6 t，并假設列車正常平穩運行時車體質量在兩個轉向架中心均勻分布，車體重力由搖枕左側A、B兩點和右側C、D兩點均勻承擔。由圖2和表1可得:

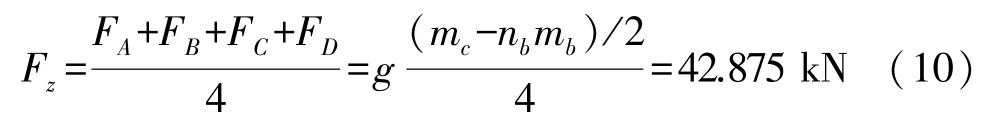
式中:Fz為A、B、C、D各點上所受載荷力均值。在此基礎上，依據《TB/T 2368-2005動力轉向架構架強度試驗方法》[19]中的垂向載荷工況，結合常規運行條件下車體側滾和車體垂向運動(浮沉)引起的垂向力動態變化，設置了5種正常運營工況(如表2)。表2中側滾系數φ取值0.15，浮沉系數φ取值0.25。

表2 模擬構架運營載荷工況組合表

構架結構模型采用圖1所示模型，載荷按25∶1等比例縮小[8]。考慮到客車正常運營過程中載重會變化，以工況1為例，取整車車廂質量波動范圍約為49 t~69 t，由式(10)計算工況1下兩側梁4個測點載荷范圍為1 715 N至2 701 N，以34 N為間隔均分為30個載荷樣本。全部工況下各測點的載荷如表3中所示(共150種正常狀態)。

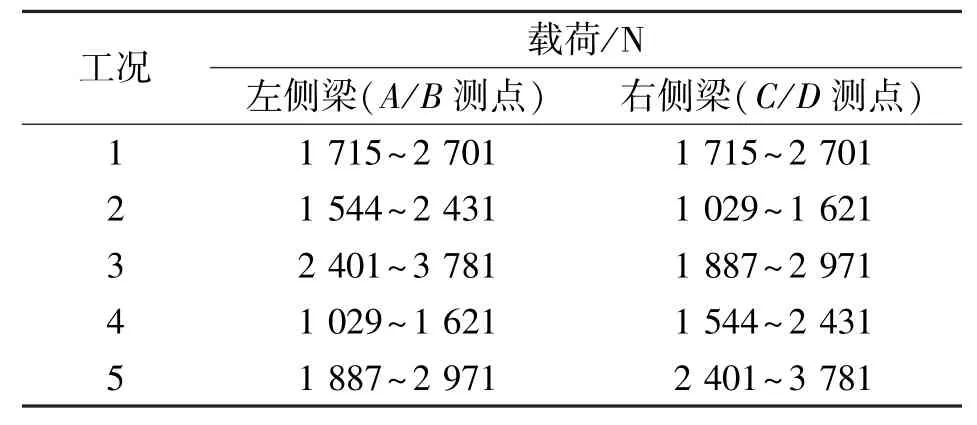
表3 模擬構架運營載荷工況組合表(具體值)

施加載荷的方式為:將構架反置于千斤頂上，通過四個拉力繩將其固定于花崗巖底座；千斤頂產生的力模擬為一節車體的重力，拉力繩產生的拉力作為輪對支撐板對構架的支持力，壓力傳感器和壓力顯示儀用于監測千斤頂施力的大小。整個應變監測實驗平臺如圖5，主要的設備參數如表4所示。

圖5 應變監測實驗平臺

表4 實驗設備參數

根據表3，每種工況包含30個不同的載荷樣本，則對于反映構架應變的信號矩陣S為:

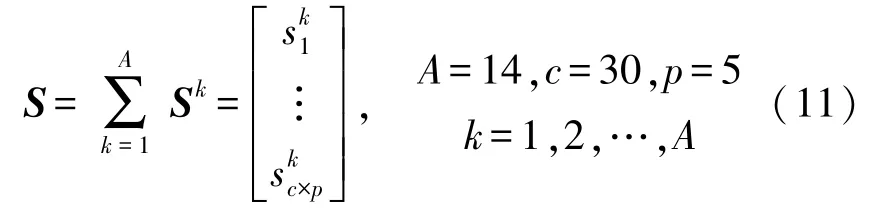
式中:p表示有多少種工況，A為傳感器備選點總數，c為每種工況下對應不同載荷的應變數據。即Sk為第k個傳感器備選點對所有工況的響應信號矩陣，S為所有傳感器備選點對所有工況的響應信號矩陣。

4.2 傳感器網絡優化結果

在NSGA-II算法中設置好初始參數，迭代終止次數T＝1 000，交叉概率pc＝0.3，變異概率pm＝0.2，初始種群個數n＝200，和傳感器備選位置總數A＝14。經優化后的傳感器分布非劣解集如表5所示。

表5 傳感器分布優化結果

4.3 多工況下構架異常狀態識別

根據相似原理，同樣以25∶1的比例將日本新干線上列車轉向架的14 cm長裂紋進行縮小，在構架模型橫梁與側梁連接處加工一道約深5 mm、寬1 mm的裂紋，裂紋位置[20]和裂紋細節如圖6所示。根據傳感器分布優化的結果，用搭建好的應變監測實驗平臺獲取構架有裂紋狀態下在不同工況的異常狀態響應數據。除增加一道構架裂紋外，異常狀態的載荷工況與構架正常狀態的一致(共150種異常狀態)，同樣采用表3作為其載荷工況組合進行載荷施加，獲取每種工況下的30個不同載荷樣本。

圖6 構架模型結構裂紋位置示意圖

采集設備與采集正常狀態下構架的應變響應數據的設備一致，步驟一致，根據式(11)其采集到的構架異常特征響應數據為:

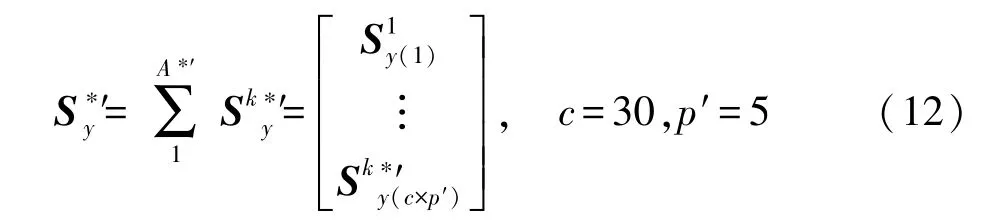
式中:p′表示有多少種工況，c為每種工況下對應不同載荷的應變數據，A*′為同一非劣層級下不同傳感器網絡中傳感器的個數，k*′為對應的傳感器網絡中的傳感器備選點位置。對于第1非劣層中應變傳感器網絡而言{A*′＝1，2，3}，{k*′＝[8]，[6、7]，[6、7、8]}；對于第2非劣層中應變傳感器網絡而言{A*′＝1，2，3}，{k*′＝[7]，[6、8]，[6、8、9]}。

用于測試的構架異常狀態數據集如式(12)所示。根據式(11)，提取優化后應變傳感器網絡對應的構架正常狀態數據集，用于SVDD建模，如下式所示:

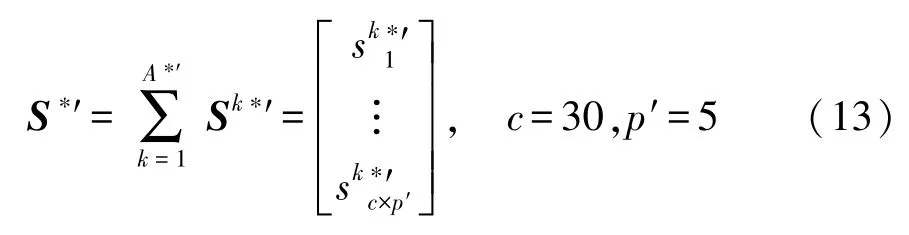
將優化后應變傳感器網絡對應的構架正常狀態數據集，并代入SVDD參數(罰參數C，核參數σ；C＝0.25，σ＝16)，建立超球體模型，進行多工況多載荷狀態下的構架異常狀態識別，識別流程如圖7所示。

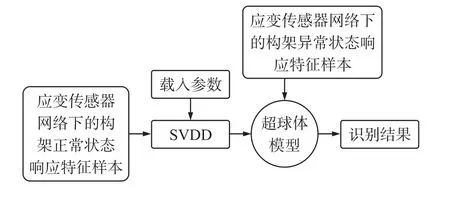
圖7 構架狀態監測流程

根據優化后的應變傳感器網絡對于第1非劣層的應變傳感器網絡，以及對于第2非劣層的應變傳感器網絡識別效果如表6所示。

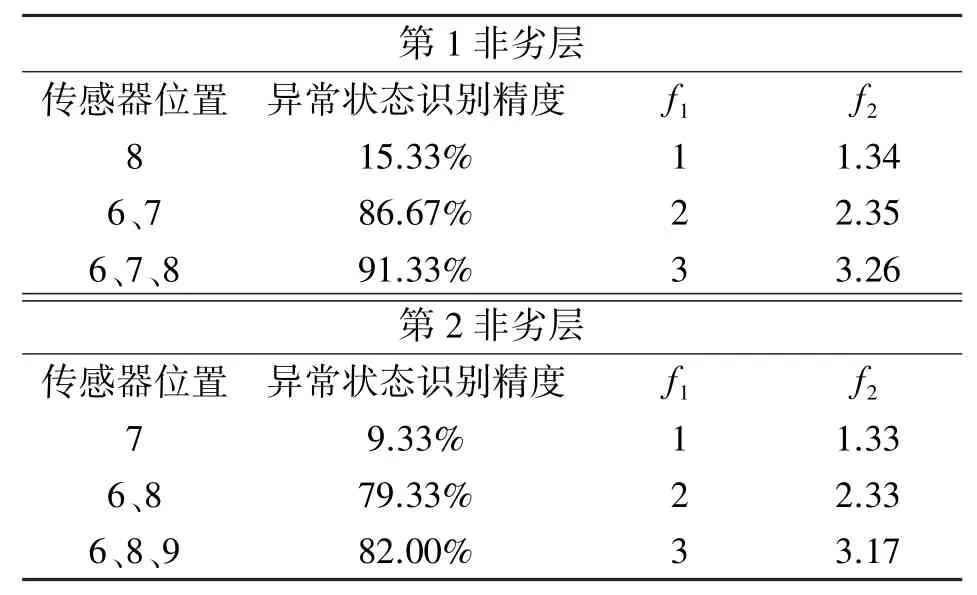
表6 不同傳感器網絡下構架異常識別效果

實驗結果與分析:

①對于應變傳感器網絡，當采用第1非劣層的傳感器布置位置時，構架異常狀態識別精度分別為:15.33%，88.67%，91.33%。結果表明，對于優化后的傳感器網絡，對構架異常狀態的識別效果都隨著傳感器數量的增加而改善，驗證了傳感器優化網絡的合理性。

②對于應變傳感器網絡，當采用第2非劣層的傳感器布置位置時，構架異常狀態識別精度分別為:9.33%，79.33%，82.00%。結果表明，對于優化后的傳感器網絡，均比采用第1非劣層的傳感器布置位置時，構架異常狀態識別精度要低，且當傳感器數量f1不變時，異常狀態識別精度與超球體聚類指標f2相關聯。

③對比1、2、3個傳感器的第1非劣層的布置方式和第2非劣層的布置方式。可以看出，在研究中，相比于超球體聚類指標f2，傳感器數量f1對構架異常狀態識別精度的影響更大。

5 結論

針對轉向架構架狀態監測建模面臨的異常狀態復雜多樣性及監測中傳感器的分布優化問題，研究針對構架異常狀態下樣本集的隨機多樣和不確定性，引入SVDD算法，以構架正常狀態(共150種)的應變樣本集構建SVDD超球體模型對多工況多載荷水平條件下構架的異常狀態(共150種)進行識別。同時以SVDD超球體半徑定義優化目標函數f1(傳感器數量)和f2(超球體聚類指標)，并基于NSGA-II算法對傳感器分布進行了優化。在此基礎上，搭建轉向架構架狀態應變監測實驗平臺，對多工況條件下構架的異常狀態識別進行研究。結果表明:

①經NSGA-II優化后的傳感器分布方案能以較少的數量保證很好的構架異常狀態監測效果，研究表明當傳感器分布優化方案中傳感器數量為3個時，異常狀態識別率已達到91.3%。

②以轉向架構架正常狀態樣本集構建的SVDD模型對異常狀態具有很好的識別效果，較好的解決了構架異常狀態下樣本集的隨機多樣和不確定性問題。