基于DKF的IMU誤差預測算法

秦閃閃，陳夏蘭，徐 穎，馬滿帥，王 瑩，梁任騰，楊子佳

(1.中國科學院空天信息創新研究院導航系統部，北京 100094；2.中國科學院大學電子電氣與通訊工程學院，北京 100049；3.北京信息科技大學信息與通信工程學院，北京 100192)

0 引言

全球導航衛星系統(Global Navigation Satellite System，GNSS)/慣性導航系統(Inertial Navigation System，INS)組合導航的核心是如何有效地將GNSS觀測量與慣性測量單元(Inertial Measurement Unit，IMU)測量結果結合得到載體導航結果的最優估計，在目前的組合導航技術中，包括松耦合、緊耦合和超緊耦合[1]。其中松耦合在軟件層面組合，將GNSS接收機導航定位結果和INS測量結果進行濾波融合[2-3]，當前常用的融合算法是卡爾曼濾波(Kalman Filter，KF)[4-5]。KF利用GNSS觀測量和IMU測量結果解算得到IMU誤差的估計值，再將估計值反饋給IMU，IMU測量結果經過估計值校正后作為導航解輸出。GNSS/INS組合導航系統長時間運行的精度更多地依賴于GNSS，然而實際中存在各種隨機的或復雜的誤差源，如可見衛星數目、多徑效應和儀器內部的量測噪聲等，都會使得衛星導航系統的量測噪聲隨時發生變化，標準KF難以對上述變化進行檢測和調整，導致其使用的噪聲統計特征與事實發生偏差，無法得到最優濾波結果，甚至會出現濾波發散現象[6]。為了克服標準KF在組合導航中應用的缺點，研究者們開始針對其設計與應用場景相適應的濾波算法。

針對全球定位系統(Global Positioning System，GPS)測量值發生較大變化時如何提高KF的濾波精度和魯棒性的問題，卞鴻巍利用對實際新息的測量計算直接修正卡爾曼濾波器增益，但需要采用GPS測量系統為INS提供外部修正信息[7]。付夢印研究了應用于慣性技術領域的相關法自適應濾波和Sage-Husa 自適應KF，然而帶有衰減因子或記憶因子的卡爾曼濾波器系統狀態維度增加，計算量加大[8]。高為廣和楊元喜使用反向傳播(Back Propagation, BP)神經網絡在線修正自適應濾波器的預測值，該算法提高了濾波精度和可靠性，但算法中提到的“經過復雜函數映射到當前函數的網絡預測值”難以獲取[9]。M.Narasimhappa等優化了Sage-Husa自適應魯棒KF算法，更新了自適應比例因子的計算方法，從而有效降低了估計誤差的平均值和標準差，但增大了系統計算的復雜度[10]。S.Hosseinyalamdary提出了一種使用遞歸神經網絡訓練組合導航觀測模型的方法，從而克服了因INS誤差模型的復雜性導致的計算誤差，但大大增加了算法的計算量[11]。

很多高動態導航載體，如快速運動的無人機，也使用GNSS/INS組合系統來導航。由于GNSS在高動態下跟蹤環路可能失鎖，在信號被掩蓋及多徑效應等場景下測量值不準確甚至沒有，導致此時的載體只能依賴IMU進行導航，導航結果會在時間積累下迅速失去有效性。本文擬解決的問題就是在GNSS接收機輸出中斷或測量結果不可信時，如何在IMU獨立導航條件下盡可能保持較高的導航精度。關于這個問題，也有學者進行研究，如德國卡爾斯魯厄大學的研究者通過在無人機上添加磁強計和高程計以解決組合導航的這個問題[12]；荷蘭特溫特大學的研究者則將深度學習的思想引入KF，利用循環神經網絡和長短期神經網絡開展了初步的研究[11]。

1 KF算法

KF估計的未知量為狀態向量，表示為x∈Rn，其是一個時間變量，即xt表示時刻t的狀態向量。其與過去直到現在的觀測矢量z1∶t相關，z∈Rm。設初始狀態為x0，則xt的概率為Pr(xt|z1∶t,x0)。根據極大似然估計(Maximum Likelihood Estimation，MLE)

(1)

系統當前的狀態與過去的狀態有關，即

(2)

去掉常數

(3)

應用前一個狀態向量的邊緣化得到基于前一個狀態向量的狀態向量估計，即

Pr(x1∶t-1|z1∶t-1,x0)dx1∶t-1

(4)

基于馬爾可夫假設，即

Pr(xt-1|z1∶t-1,x0)dxt-1

(5)

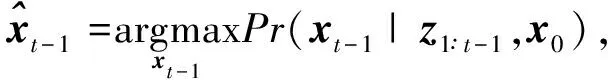
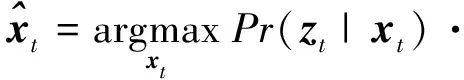
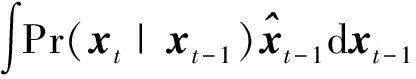
(6)

在KF中，系統狀態與上一時刻的狀態和系統模型有關，即

xt=f(xt-1)+εt

(7)

式中，εt為系統噪聲模型。同時系統狀態通過觀測方程g映射到觀測量zt∈Rm，即

zt=g(xt)+ωt

(8)

式中，ωt為觀測噪聲模型。在KF中，狀態模型和觀測模型都是線性的，分別用F和G矩陣表示。系統模型為

xt=Fxt-1+εt

(9)

同理，觀測模型為

zt=Gxt+ωt

(10)

假設KF中系統噪聲和觀測噪聲都服從正態分布

εt～N(0,Qt)

(11)

ωt～N(0,Rt)

(12)

式(11)和式(12)中，Qt和Rt分別為系統噪聲和觀測噪聲的協方差矩陣。

KF過程分為預測過程和更新過程。系統當前狀態由前一時刻狀態預測，即

(13)

狀態向量的上標“-”表示預測量，上標“+”表示更新量。采用誤差傳播法，根據前一時刻狀態向量的協方差矩陣估計當前狀態向量的協方差矩陣

(14)

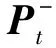
在更新過程中，當前狀態的更新值由當前觀測值和預測值得出

(15)

則狀態變量更新值的協方差矩陣為

(16)

式中，Kt為卡爾曼增益

(17)

2 深度卡爾曼濾波(DKF)

為了解決KF更新過程中觀測量獲取不到的問題，在KF中添加建模步驟，即在KF中加入隱變量。隱變量在狀態向量中不可見，但能決定狀態向量，用ht表示，是時間相關變量。當前系統狀態取決于過去T個時刻隱變量的值ht-1∶t-T。

假設當前系統狀態只與當前隱變量有關，即不直接依賴于過去系統狀態xt-1∶t-T，馬爾可夫假設不成立。新的假設不僅符合很多系統，而且簡化了計算。

設當前隱變量與過去隱變量和系統狀態之間的映射關系為φ，即

(18)

當前系統狀態直接與當前隱變量相關

(19)

(20)

(21)

式中，Wh=[Wxh,Whh]。建模任務轉化為估計Wh和Wxx。如圖1所示，深度卡爾曼濾波(Deep Kalman Filter，DKF)的上層網絡與傳統KF基本一致，建模步驟位于下層網絡。根據IMU隨時間積累的特性，在時間維度上使用深度學習算法進行建模。

圖1 DKF的概率圖模型

2.1 模型參數估計

(22)

基于式(22)的結果估計隱變量

(23)

根據式(21)，計算系統狀態可以轉化為計算Wxx，同理，計算隱變量轉化為計算Wh。將式(20)和式(21)代入式(22)，則

(24)

(25)

隱變量和狀態向量的迭代估計一直持續到算法收斂到其解，最后確定系統模型并得出狀態向量的估計。P.Mirowski和Y.Lecun的研究表明,EM算法可以使用遞歸神經網絡訓練[13]。

EM算法最終收斂到凸函數的全局最大值，然而對于一些建模為非凸函數的系統，EM很有可能收斂到局部極大值，所以如何找到式(24)和式(25)中的最大值是一個挑戰。

DKF的建模過程分為兩步：通過過去的系統狀態和隱變量估計當前隱變量；通過當前隱變量估計當前系統狀態。

用隱變量估計重新構造式(6)，則

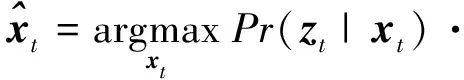
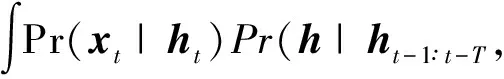
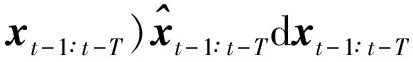
(26)

(27)

將式(21)代入式(26)，得到

(28)

則Wxx的梯度為

(29)

Wh的梯度為

(30)

利用梯度下降方法最小化能量函數。建模系統的參數矩陣Wh和Wxx為

(31)

(32)

順應時勢的轉型要求電視新聞記者在努力學習最新科學技術、傳媒技術的同時，更新理念，深化對不同業務的理解，成為一個“新聞全才”。更重要的是，媒體融合時代對主流媒體新聞記者職業操守的要求更加嚴格，電視新聞記者務須確保采編的所有新聞內容真實、客觀，并且能夠引導正確社會價值觀。在遵循媒體融合時期新聞傳播規律的基礎上，電視媒體可嘗試打造具有“標簽”效應的品牌記者，如知名調查報道記者、知名環保欄目記者、知名時政新聞記者等。

2.2 長短期記憶網絡(LSTM)

遞歸神經網絡的缺陷是梯度爆炸和梯度消失[14]。當T比較大且建模時間較長時，梯度會在幾層網絡中做乘法運算，則較大的梯度乘積更大，最終導致梯度爆炸。反之，如果梯度較小，乘積則趨近于零，從而導致梯度消失。為了抑制遞歸神經網絡中的這種效應，長短期記憶網絡(Long Short-Term Memory，LSTM)中采用了門記憶[15]，計算單元具體結構如圖 2所示。

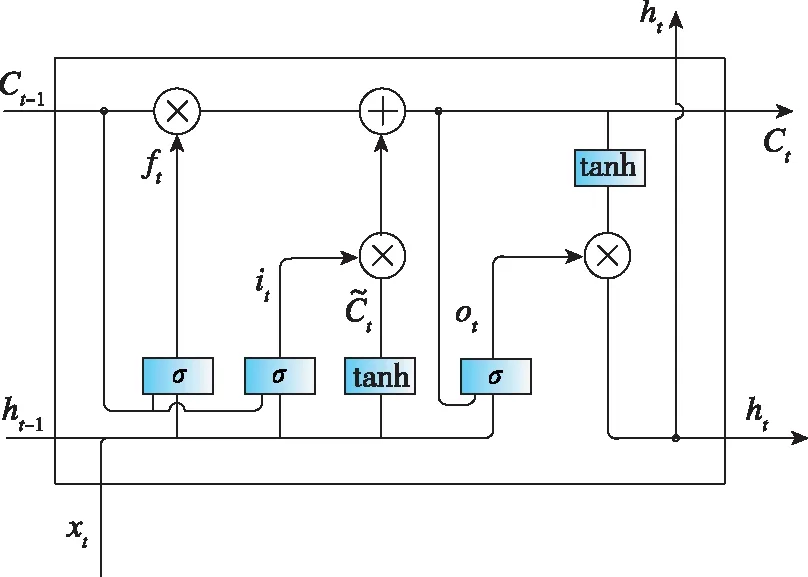
圖2 LSTM(Peephple connection)結構圖

LSTM在遞歸神經網絡中加入了判斷信息是否有用的處理器——cell，一個cell當中放置了三扇門，分別叫作輸入門、遺忘門和輸出門。用it表示輸入門，ot表示輸出門，ft表示遺忘門，這三種門都可以用線性函數和非線性函數的組合來表示

(33)

式中，σ表示非線性函數，線性函數由參數矩陣表示。cell的狀態ct和隱藏層ht按如下計算

ct=ft°ct-1+it°tanh(Wxxt+Whht-1)

(34)

(35)

式中，°表示按位相乘。對于具有長期相關性的輸入數據，輸入門可以保持以前狀態向量的信息，并且可以訪問以前狀態向量的梯度。因此，梯度在反向傳播過程中不會爆炸或消失。遺忘門控制了模型的復雜性，并刪除了不相關的過去狀態向量。

基于DKF的導航系統分為訓練部分和應用部分。已經知道的是：如果GNSS測量值能夠得到，將其作為觀測值輸入到KF中，應用系統模型和觀測模型來預測和更新系統狀態，同時使用DKF對IMU模型進行訓練，如圖3(a)所示；如果GNSS失鎖或其他無法獲得GNSS數據的情況發生時，KF只能完成預測過程，此時應用訓練好的模型進行導航解算，如圖3(b)所示。

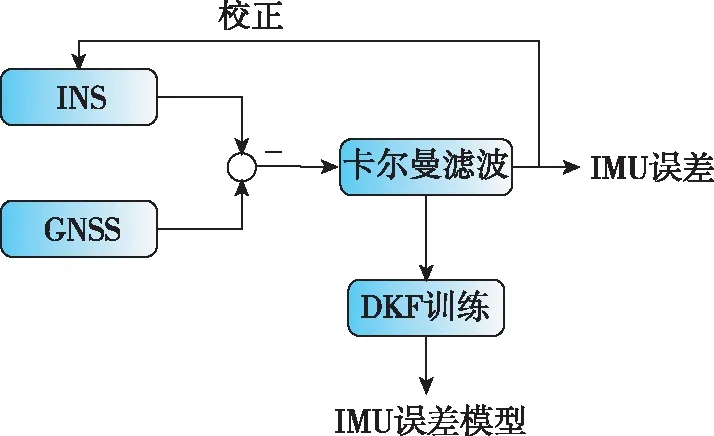
(a)DKF訓練模型

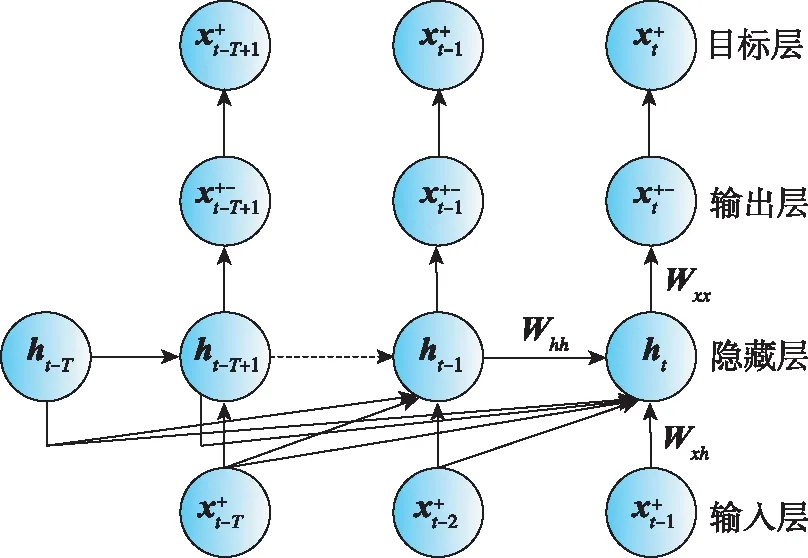
(a)DKF訓練網絡結構圖

3 基于DKF的仿真分析

以仿真數據為例對算法進行有效性驗證，仿真數據長400s，采樣頻率1Hz，包含有兩種數據：第一部分是設定的真實導航數據；第二部分是仿真輸出的IMU數據。每一秒都包含有變加速運動導航載體的實時真實速度和IMU速度信息。

在GNSS失鎖時，作為自主式導航系統，導航載體上的INS仍然正常運行，其初始導航狀態是GNSS失鎖前最后時刻輸出的導航狀態。實驗所使用的數據是長400s的含有標識的IMU數據以及在真實導航數據上仿真的GNSS數據。在GNSS失鎖時，INS單獨運行，其誤差迅速增大，失鎖200s后，東北天坐標系下3個方向的速度誤差已經分別達到1.1537m/s、1.2146m/s和0.3332m/s。

為了評估算法的結果，將400s的數據劃分為兩段：前200s數據作為訓練集，用來測試和評估；后200s數據作為測試集，用來驗證模型的有效性。前200s訓練部分，在真實導航數據上添加噪聲作為GNSS數據，將其與IMU數據組合通過KF得到IMU誤差，該IMU誤差作為DKF的訓練數據使用。后200s使用訓練得到的IMU誤差模型預測IMU誤差，用其校正IMU數據，并和設定的真實導航數據進行比較，以評估DKF的有效性。

DKF網絡設置輸入序列長度為5，中間節點數為50，迭代55次，DKF模型預測的IMU誤差結果如圖5(a)和(b)所示。

如圖5(a)所示，在GNSS失鎖后，使用DKF算法訓練的模型估計出IMU的誤差與實際IMU誤差接近，將其作為校正量代入IMU數據中，能夠保持一定時間的高精度導航。如圖5(b)所示，如果在GNSS失鎖后使用DKF進行IMU誤差校正，200s后速度誤差只增長到0.3746m/s，且200s內的平均誤差只有0.1350m/s。與GNSS失鎖200s后的系統誤差1.1537m/s相比，DKF對短期內導航解的改善是顯而易見的。

DKF通過前5個時刻預測下一個時刻的IMU誤差，平均估計使用前5個時刻的平均值作為下一個時刻的IMU誤差，兩者的對比實驗結果如圖5(c)和(d)所示。如果在GNSS失鎖后使用平均估計進行IMU誤差校正，由于平均估計預測的IMU誤差維持在GNSS失鎖時刻的數據，在200s內誤差達到1.1203m/s，200s內平均誤差為0.5890m/s。平均誤差對于GNSS/INS組合系統的持續導航改善不如DKF。

GNSS失鎖后，GNSS/INS組合系統由于丟失觀測量而無法使用KF，但是基于持續輸出的IMU數據，可以使用卡爾曼的預測部分對IMU誤差進行估計，卡爾曼預測和DKF的對比實驗結果如圖5(e)和(f)所示。如果在GNSS失鎖后使用卡爾曼預測進行IMU誤差校正，其估計的IMU誤差在200s內達到0.7479m/s，200s內平均估計誤差為0.4421m/s。卡爾曼預測對于GNSS/INS組合系統的持續導航改善不如DKF。

最小二乘估計作為常用的估計方法，在曲線擬合方面效果顯著，可以使用最小二乘估計擬合GNSS未失鎖前的IMU誤差模型，從而預測GNSS失鎖后的IMU誤差。最小二乘估計和DKF的對比實驗結果如圖5(g)和(h)所示。如果在GNSS失鎖后使用最小二乘估計進行IMU誤差校正，其估計的IMU誤差在200s內的估計誤差達到0.9725m/s，200s內平均估計誤差為0.3352m/s。最小二乘估計對于GNSS/INS組合系統的持續導航改善不如DKF。

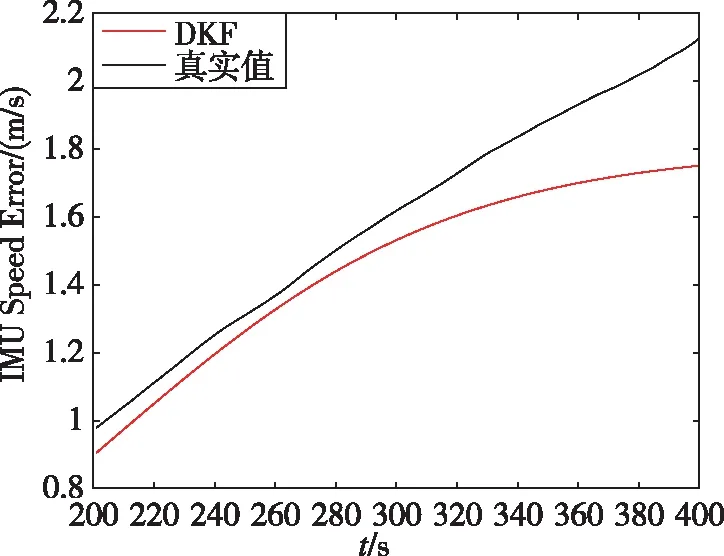
(a)DKF預測結果圖

為了進一步說明DKF算法的有效性和性能，將DKF的估計誤差與平均估計、卡爾曼預測和最小二乘估計進行對比，結果如圖6所示。

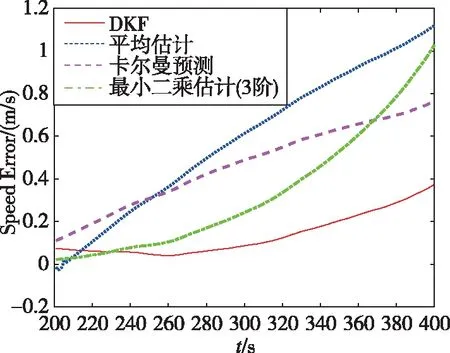
圖6 四種方法的估計誤差對比圖

如圖6所示，在GNSS失鎖200s內，對于GNSS/INS組合系統的持續導航改善最好的是DKF，其次是最小二乘估計。

4 結論

針對GNSS/INS組合系統中GNSS失鎖后導航精度的維持問題，本文提出了一種基于LSTM的DKF算法。首先使用GNSS數據和IMU數據通過KF獲取失鎖前的高精度導航數據；其次，基于高精度導航數據訓練IMU誤差模型；最后，在GNSS失鎖后使用IMU誤差模型進行誤差校正。算法分析與實驗結果表明：

1)DKF算法在時間維度上分為2個階段執行，實現了基于歷史信息對當前IMU誤差的校正。因此具有比傳統KF更高的信息利用率，可以在GNSS失鎖時維持GNSS/INS組合系統的高精度運行。

2)本文提出的DKF算法依靠LSTM對序列信息的敏感度對IMU誤差進行建模，而機器學習的本質要求含有大量信息的大數據集進行實驗。在實際的復雜環境中如何獲取這些數據并且保證算法的實時性，值得做進一步研究。