深度卷積神經網絡中激活函數的研究

李一波，郭培宜，張森悅

(沈陽航空航天大學 自動化學院，遼寧 沈陽 110000)

0 引 言

AlexNet網絡模型在圖像識別分類、目標檢測、語音文字識別等方面都表現得十分突出[1]。AlexNet雖然不是首個被創建的卷積神經網絡模型(convolutional neural networks，CNN)，可是它是首個引起眾多研究者所關注的卷積神經網絡，具有里程碑意義。AlexNet模型是由多倫多大學教授Geoffery Hinton同他的學生Krizhevsky等人共同設計，2012年創下Imageclassification比賽的新記錄，并獲得了ImageNet Large Scale Visual Recognition Challenge(ILSVRC)挑戰賽的冠軍[2]。同年，Krizhevesky等[3]在大型圖像數據庫ImageNet[4]的圖像分類競賽中提出的AlexNet模型，以超越第二名11%的精確度獲得了冠軍，使得卷積神經網絡成為學術界關注的焦點之一。隨著機器學習研究領域的不斷拓展，AlexNet也被許多學者作為首選的網絡模型，通過改進和優化，其分類精度不斷提高。

深度卷積神經網絡的觀點起初來源于人工神經網絡，而網絡中激活函數則是人工神經網絡模型訓練過程和學習非線性函數過程中不能或缺的一部分。如果網絡模型不使用激活函數，神經網絡每一層的輸出都將等價于前一層輸入的線性函數，那么無論神經網絡將會有多少層，輸出都將是輸入的線性組合，這種情況使網絡模型成為最基本的感知器，深度神經網絡將變得失去本身意義[5]。因此，使用激活函數作為神經元來引進非線性因素是十分必要的，可以使得神經網絡能夠任意逼近任何非線性函數，進而使神經網絡能夠應用到更多的非線性模型中。Krizhevsky等人在AlexNet中提出了ReLU激活函數來訓練網絡[6]，其優點是前向區間為線性函數，加快了模型訓練的收斂速度，解決了softsign、Softsign、Tanh等常見激活函數中的梯度消失問題，然而ReLU激活函數很可能導致一些神經元在模型訓練中無法激活。為了解決這種神經元“死亡”現象，改進了ReLU激活函數，使其在x小于零的負軸區間由Swish函數來替代，使負半軸的ReLU激活函數稱為非線性激活函數，有效地解決了x小于零的部分神經元不能激活的問題，并且在x大于零的區間部分范圍內由ReLU激活函數來替代，提高收斂速度的同時也能夠提升參數的利用率，并且降低了過擬合現象的發生率，很好地提高了AlexNet的魯棒性。

針對AlexNet網絡中激活函數ReLU在網絡訓練中產生的神經元死亡和均值偏移問題，結合反正切函數和對數函數的優勢，在傳統激活函數ReLU基礎上提出了一種新的激活函數sArcReLU。將文中構建的激活函數訓練網絡模型并應用于公開數據集分類實驗中以驗證其建立的網絡的性能。實驗結果表明，利用sArcReLU激活函數訓練的深度卷積神經網絡在分類精度和適應性方面均有明顯的改善。

1 AlexNet模型結構

AlexNet總共有650 000個神經元，63 000萬個神經連接，60 000 000個網絡參數。AlexNet網絡結構簡單，引入了許多新方法來達到穩定的收斂速度[7]，網絡結構如圖1所示。網絡模型結構共8層，其中分別含有五層卷積層和三層全連接層，包括了LRN局部響應歸一化層和Dropout正則化。此網絡模型在圖像分類領域有著較為出色的優勢[8]。

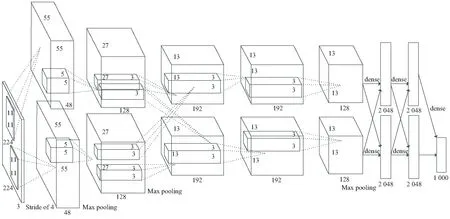
圖1 AlexNet結構模型

圖像數據輸入格式是227×227×3，其中227表示輸入圖像的寬度和高度，3表示輸入圖像的三原色R、G、B通道模式，所以不需要對輸入的數據集進行額外的格式裁剪。第一、二層計算均為卷積，ReLU，最大池化層和歸一化，第二層的輸出結果與256個特征圖進行了卷積操作。網絡中的第三、四層只需要進行卷積和ReLU操作。第五層的過程和第一層的過程類似，區別只在于沒有經過歸一化處理。網絡最后將其第五層的輸出轉變為長向量，輸入到三層全連接結構的卷積神經網絡模型中，再運用Softmax回歸函數即可計算其分類準確值。

2 模型的改進

AlexNet網絡采用ReLU非飽和線性函數，激活值的獲取相對簡單，只用一個閾值，省去了原本復雜的運算過程，相較于常見的非線性S型激活函數Tanh、Sigmoid等收斂速度更快[9]，改善了梯度消失和收斂不穩定的缺點。圖2為ReLU與其他常見激活函數的曲線對比。

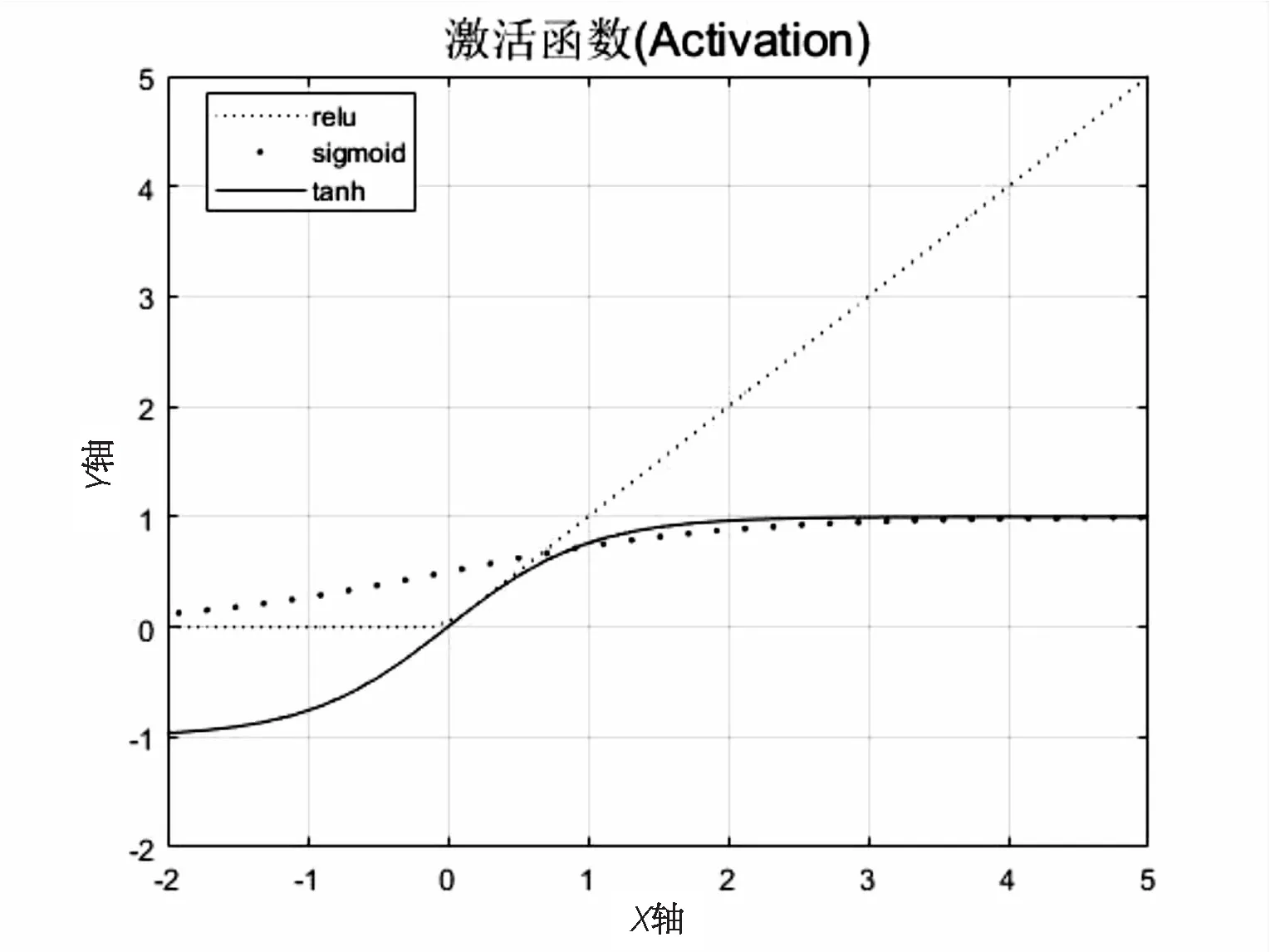
圖2 ReLU與常見的激活函數曲線對比

Tanh函數換言之是Sigmoid函數的一種變換類型，Tanh函數的輸出值在[-1,1]區間內，而Sigmoid函數的輸出值則在[0,1]區間[10]。Tanh和Sigmoid都擁有飽和區，ReLu函數在x大于零時導數一直是1且不變，十分有助于解決梯度消失、梯度爆炸等問題，促使加快訓練速度。

一般地，當網絡模型后向傳遞過程時，且使用梯度下降法求解網絡參數，Sigmoid激活函數向下傳導的梯度中包含了有關自身輸入的導數f'(x)，當輸入值進入飽和區時，f'(x)的輸出值逐漸接近于零。此特性十分容易導致梯度消失現象，所以深度神經網絡一直很難得到有效的訓練，也是阻礙神經網絡發展的重要原因之一[11]。

其中ReLu激活函數的數學表達式為：

f(x)=max(0,x)

(1)

經過圖2分析，ReLu激活函數曲線也存在很多不足，例如當輸出值恒大于或等于零時，易導致均值偏移的缺點，均值偏移會導致神經元將前一層網絡的非零均值輸出的信號作為輸入信號，使參數的計算復雜度大幅度增加。處于網絡模型訓練過程的前向傳播過程時，“強制”稀疏性作用會使網絡中的某些神經元一直不會被激活，與其相對應的參數也一直不會被更新，所以會致使一些好的特征被屏蔽。眾所周知，神經“死亡”和強制稀疏性的缺點對網絡模型的收斂速度和網絡性能影響很大[12]。

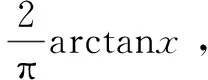
(2)

ArcReLU函數導數如下：

(3)

由圖3分析，ArcReLU激活函數導數值恒為正值。根據導數特征，可說明函數明顯呈單調遞增特性。當激活函數擁有單調特性時，單層網絡能保證其為凸函數，由此推斷出該函數在訓練過程中更易收斂。

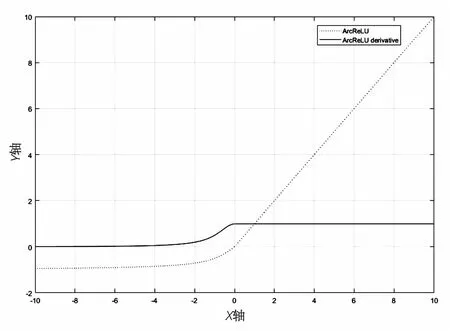
圖3 ArcReLU及其導數的圖像

由于ReLU歸類于分段線性非飽和的函數，其與傳統的S型激活函數作對比發現，ReLU函數隨機梯度下降收斂速度更快，而且函數計算過程更加簡潔明了。相較于Sigmoid激活函數，ReLU稀疏特性更加明顯。然而稀疏性也將會帶來更高的錯誤識別率并且降低了網絡模型的有效容量。通過分析激活函數，不僅計算過程更加簡潔，而且負半軸的輸出會得以更好的保存。在負軸使用了反正切函數進行替換，不僅可以使均值更趨向于零，緩解了函數均值易偏移的缺點，并且其負半軸部分具有軟飽和性，使其不會輕易出現神經元“死亡”的現象，同時具備單調遞增的特性，進一步提高了收斂速度。

文中結合ArcReLU激活函數設計了一種新的激活函數，記為sArcReLU，表達式如公式(4)所示，函數圖像如圖3所示。

(4)

上述公式中，系數s表示超參數，取值范圍為[0,1)。當輸入為負值時，函數的梯度與參數s不相關；當輸入為正值時，函數值取決于超參數。

改進后激活函數的圖像如圖4所示。由函數圖像分析可以得到初步結論，該函數在其定義范圍內可導并且單調遞增，現只需證明該函數在其原點處的可導特性。以下證明過程中將x大于零的部分稱為f1，x小于等于零的部分稱為f2，過程證明如下：

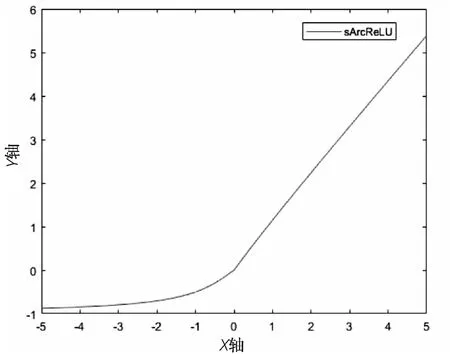
圖4 sArcReLU函數圖像

f(0)=f(0-)=f(0+)=0

(5)

(6)

(7)

式(5)說明sArcReLU在原點連續且具有定義。由式(6)與式(7)的結果分析，函數都存在且相同，依據導數的定義，該函數在零點處可導。

sArcReLU的偏導數為：

從上述公式可看出，sArcReLU激活函數的導數值始終大于零。根據導數定義，證明函數具有單調遞增特性。當激活函數始終具有單調特性時，單層網絡可以保證其為凸函數[14]。當激活函數中x大于等于0，即神經元處于興奮激活狀態時，梯度隨著x的增加而不斷下降，并且最終收斂于1。當x小于零，即神經元處于抑制區域時，具有接近于零的梯度s。

sArcReLU函數具有以下優勢：

①負軸的輸出值保持非零值，因此激活函數擁有保留梯度變化的特性，即可以有效解決由ReLU強制置零特性導致的神經元“死亡”缺點。

②超參數s使得激活函數輸出值可變，消除了當ReLU取正值時的線性特性，使得網絡更新過程更接近于生物神經元接收刺激信號時展現的生物特性，并且應用于不同的數據集將會得到不同的最優值，也使改進后的激活函數更具備適應性。

③由于超參數s的存在，正半軸的值保持可變性，可以實時修正數據的分布稀疏性，保留了網絡快速收斂的特性。

3 實驗與分析

UC Merced Land Use(UCM)數據集為公開的遙感數據集。數據集中的遙感圖像由工作人員從美國地質調查局“市區圖像”集合中的大圖像中手動提取[15]。其中包括美國不同城市地區的21種地物的遙感圖像，數據集中每一類有一百幅，共2 100幅，空間分別率為1英尺，分別具有R、G、B三個顏色通道。21類場景分別為農田、機場、棒球場、沙灘、建筑、叢林、密集住宅區、森林、高速公路、高爾夫球場、港口、十字路口、普通住宅區、房車停車場、立交橋、停車場、河流、跑道、高級住宅區、儲油罐、網球場。其中部分場景之間有部分重疊，比如住宅區分了密集住宅區、普通住宅區、高級住宅區三類。21類場景圖像的部分樣例如圖5所示。

圖5 UCM數據集樣例圖

實驗采用開源框架Tensorflow-1.10.0，編程軟件python3.6.6實現模型結構構建，采用的CPU是Intel(R)Core(TM)i5-8500 CPU @3.00 GHz，8G內存，64位windows10操作系統。

按照9∶1的比例將UCM數據集中每一個場景的高分辨率圖像隨機分為90張訓練數據、10張測試數據。初始學習率選取0.000 1、0.001、0.01、0.1、1，實驗結果如圖6所示。

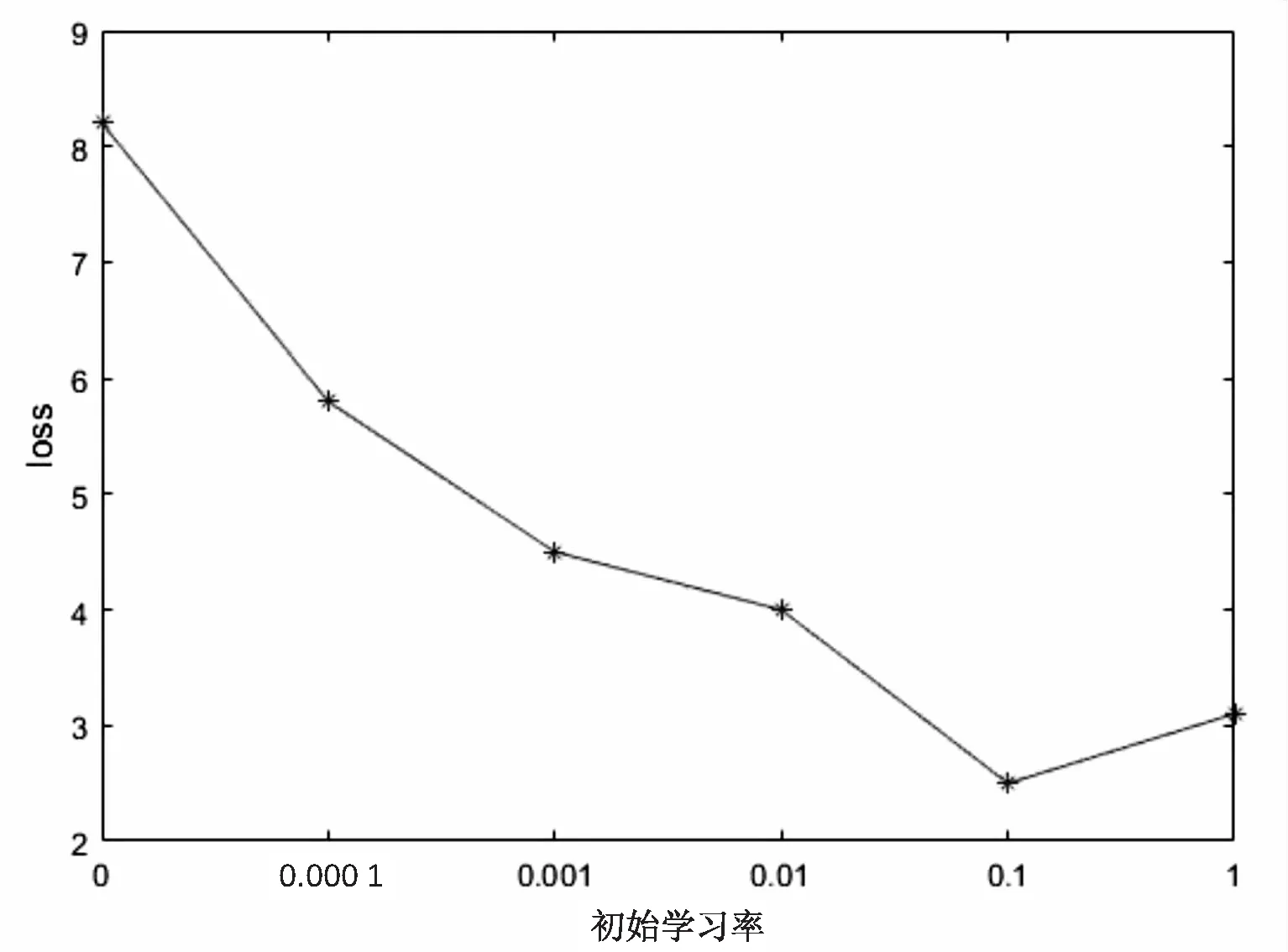
圖6 不同初始學習率對應的loss值

隨著學習率不斷擴大，網絡的損失值逐漸減小，隨后loss值又開始小幅度增大。由圖6分析選取0.1作為初始學習率最為合適。

為了驗證激活函數參數s取值對分類結果的影響，s分別取值0,0.01,0.1,0.4,0.7,1進行測試，實驗結果如表1所示。

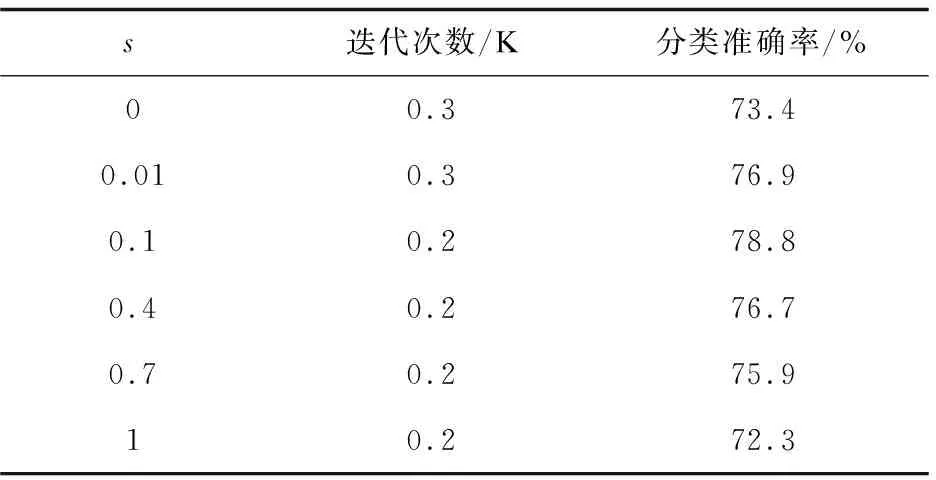
表1 超參數s分析

實驗結果表明，當s=0時，激活函數退化為ReLU，準確率就是AlexNet經典網絡模型訓練得出的結果，即73.4%。當s=0.1時，網絡會在1 000次時最先達到收斂狀態，而且分類效果最好，網絡準確率將會達到78.8%。

在數據集UCM和同等條件下對三種激活函數ReLU、ArcReLU、sArcReLU做了訓練測試。實驗結果如表2所示。

表2 數據集UCM下的準確率

通過結果分析，用sArcReLU激活函數訓練的AlexNet在分類準確率上比受其他兩個激活函數的AlexNet更勝一籌。

為了驗證提出的激活函數的適應性，新建了一個數據集UCM-NWPU，選取NWPU-RESISC45和UCMerced_LandUse中相同15種場景，每種場景有900張，總有13 500張，對圖像尺寸歸一化，調整輸入圖像的尺寸統一為256×256×3。訓練集是在每類圖像場景中隨機挑選出其中90%圖像，因此原有訓練集共有12 150張圖像，剩下的1 350張圖像就將作為測試集。

若選取的學習率過大，十分有可能會直接越過最優值；若選取的學習率過小，優化的效率可能過低，長時間就無法收斂。同上一個實驗一致，經過測試，本實驗的學習率為0.1時測試結果最好，激活函數中超參數s選取0.1時效果最好。實驗結果如下所示：

圖7和圖8分別是sArcReLU作為激活函數在數據集UCM-NWPU上訓練驗證的分類準確率和損失函數曲線。

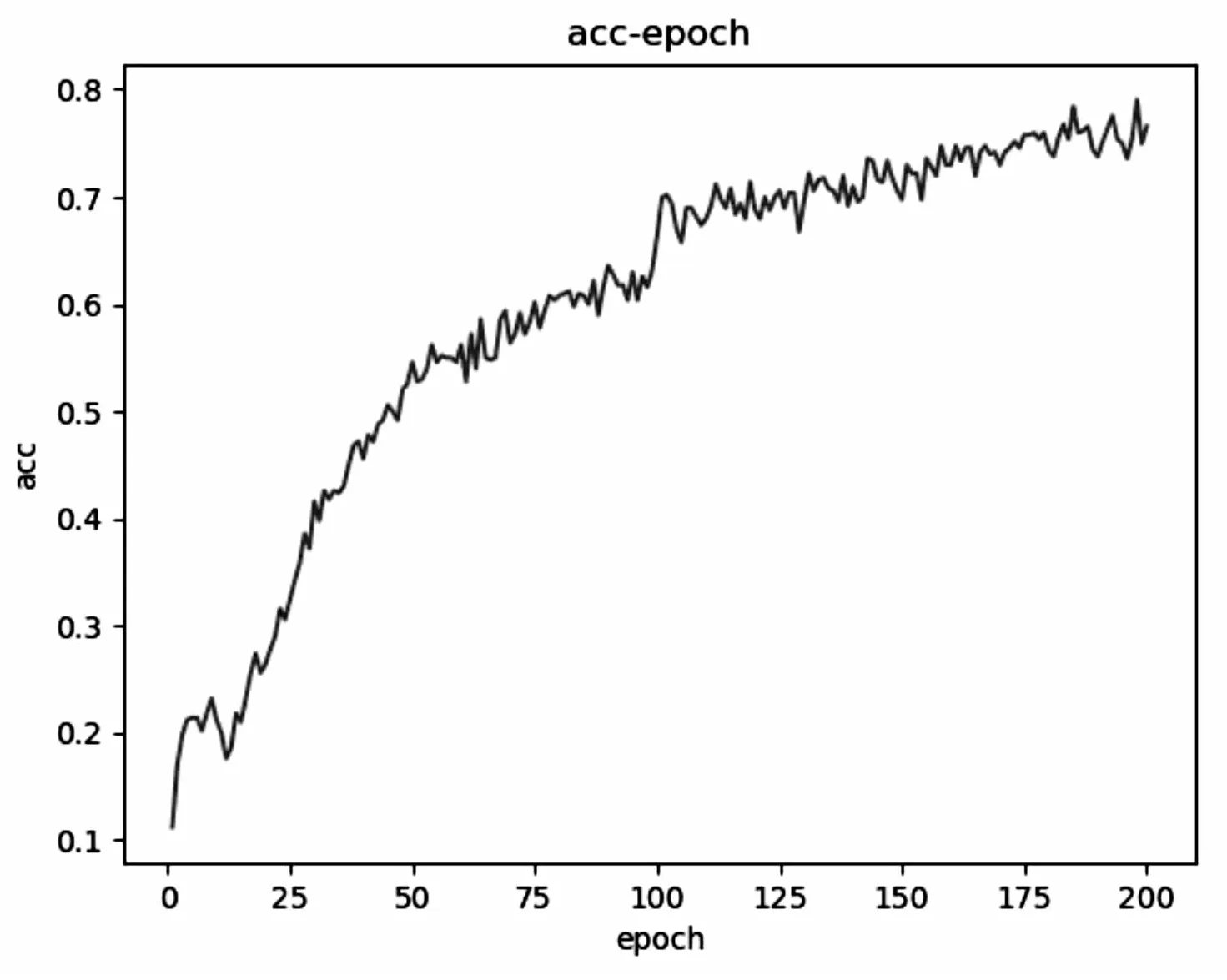
圖7 準確率

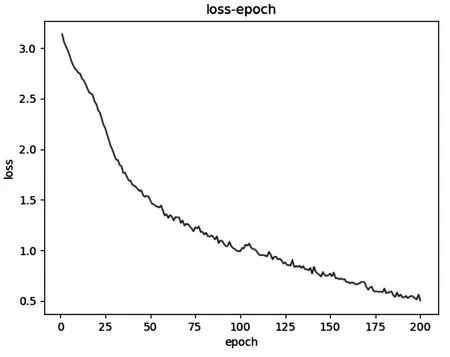
圖8 損失函數曲線

4 結束語

文中設計了一種新激活函數sArcReLU，并且與ReLU和ArcReLU激活函數進行了實驗分析和比較。實驗證明：sArcReLU激活函數能夠明顯提高網絡迭代速度并且有效降低訓練的誤差率。表明sArcReLU中超參數s對迭代次數和準確率有一定的影響。下一步研究工作的重點將放在激活函數中超參數s的優化上，以進一步提高激活函數sArcReLU的性能。