基于波數-頻率譜的腔體流動自持續振蕩頻率研究
倪小松,肖新標,劉浩楠
基于波數-頻率譜的腔體流動自持續振蕩頻率研究
倪小松,肖新標*,劉浩楠
(西南交通大學 牽引動力國家重點試驗室,四川 成都 610031)
在目前普遍認可及廣泛應用的腔體流動自持續振蕩噪聲頻率預測方法Rossiter半經驗公式中,只給出了經驗常數的推薦值,并沒有給出具體的計算方法。為此,本文采用數值模擬的方法確定值。首先,采用LES湍流模型建立腔體自持續振蕩噪聲預測模型。進而,分析腔體內部監測點,得到前三階噪聲峰值頻率,并與取推薦值(0.57)的Rossiter公式預測頻率進行對比,預測結果存在一定的誤差。然后,通過分析腔體后緣湍流脈動壓力的波數-頻率譜,得到值為0.63并代入Rossiter公式,得到前三階噪聲峰值頻率并與數值模擬結果吻合較好。結果表明,利用分析湍流脈動壓力的波數-頻率譜確定經驗常數的方法是可行的,并且能夠提高Rossiter公式預測頻率的準確性。
腔體流致噪聲;峰值頻率;Rossiter公式;波數-頻率譜
腔體結構廣泛存在于航空航天、航海、汽車、軌道交通等領域,如戰機上的武器艙、船舶上的流水孔、汽車的天窗以及高速列車的車廂連接處。當腔體結構高速運行時,來流撞擊到腔體后緣,復雜的反饋過程會使空腔上方剪切層形成持續振蕩,從而導致空腔產生強烈的噪聲,屬于簡單的流體動力學作用。當剪切層的自持續振蕩頻率與腔體結構的聲學特性(Helmholtz共振或聲學駐波模態)發生耦合時,腔體的噪聲峰值將進一步加大,屬于流體聲學共振作用。當剪切層的自持續振蕩頻率與腔體自身結構的振動固有模態發生耦合時,會產生強烈的峰值噪聲且加速腔體結構的疲勞,屬于流體彈性作用[1-2]。在流體聲學作用和流體彈性作用中,剪切層自持續振蕩都起到了一個“放大”的作用。為控制腔內噪聲以及延長腔體結構壽命,剪切層自持續振蕩頻率和機理一直是廣大學者研究的熱點。1964年,Rossiter[3]在對投彈艙噪聲進行研究時推導出了預測剪切層自持續振蕩頻率的半經驗公式,并將經驗公式與試驗數據對比,證明了公式的準確性。
Rossiter公式自被提出以來,就受到相關學者的廣泛應用和認可,但對于公式中兩個經驗常數(相位延遲系數)和(湍流運動速度與自由來流速度之比)Rossiter并未明確給定。一般情況下取0.25[3-4];而的取值對預測結果有著重大影響,實際上是一個范圍值,它與腔體前緣湍流邊界層厚度和腔體開口長度有關,一般需要通過試驗測得。East等[4]通過試驗測得該值的范圍為0.35~0.6;Ma等[5]研究以往的流致共振總結出的范圍則比East的小,為0.22~0.43。
通過風洞試驗的方法雖然能夠準確計算出值,但腔體結構樣件制作麻煩,且風洞試驗成本昂貴,會耗費大量的財力物力。隨著計算機的發展,數值模擬能大幅度降低研發成本,提高產品質量[6]。CFD(Computational Fluid Dynamics,計算流體動力學)已經逐漸成為研究腔體流動效應的重要途徑。Daude等[7]采用大渦模擬(LES,Large Eddy Simulation)的方法對空腔流動中不穩定性的被動控制進行了研究并與試驗數據對比,證明了LES方法的可靠性。楊國晶[8]采用LES方法對陷下式腔體的流動特性進行了一系列的參數調查,并與試驗結果相比較,證明了數值模擬的準確性。Li等[9]采用隱式LES方法研究了矩形腔體在來流馬赫數大于1時渦脫落和聲激勵的關系,結果驗證了聲激勵的反饋是腔體形成自持續振蕩的主要原因。鄧玉清等[10]采用LES方法對腔體壁面湍流脈動壓力進行監測并得到其波數-頻率譜,并從波數頻率譜中得到湍流運動速度和能量分布等結果。
可見,數值模擬在研究腔體流動問題上得到了學者的認可,且在試驗中也得到了驗證。因此,在腔體設計前期為了節約風洞試驗成本,本文提出采用LES方法,通過計算腔體后緣壁面湍流脈動壓力,得到湍流脈動壓力的波數-頻率譜,通過分析湍流脈動壓力的波數-頻率譜,得到湍流的運動速度,從而確定Rossiter公式中的值,提高渦脫頻率預測的準確性。
1 Rossiter公式與計算方法
1.1 Rossiter公式
渦撞擊到腔體后緣產生的聲渦將會向上游運動,引發腔體前緣渦脫落,該渦運動到腔體后緣時又會產生聲渦,如此往復循環形成腔體的自持續振蕩,如圖1所示。圖中:λ為聲波波長,λ為渦的波長,即兩個渦之間的間距。在初始時間=0時,向上傳播的聲波的相位假定為零,并且腔體跨越n個完整的波長λ,這時,距離腔體后緣γλ(γ為兩運動之間的相位差)處有一個渦;當=時,渦繼續以運動速度kU向下游行進,向上游傳播的聲到達上游進而誘發新渦的產生。
以上渦和聲的運動,存在著以下的關系:
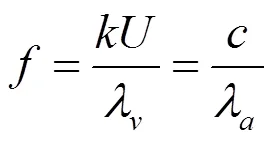
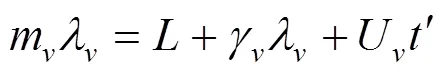
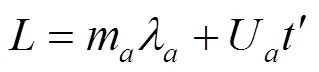
式中:為腔體自持續振蕩頻率,Hz;為聲速,m/s;U為渦的運動速度,m/s;U聲渦的運動速度,m/s;m、m分別為聲波和渦的波數,皆為整數。
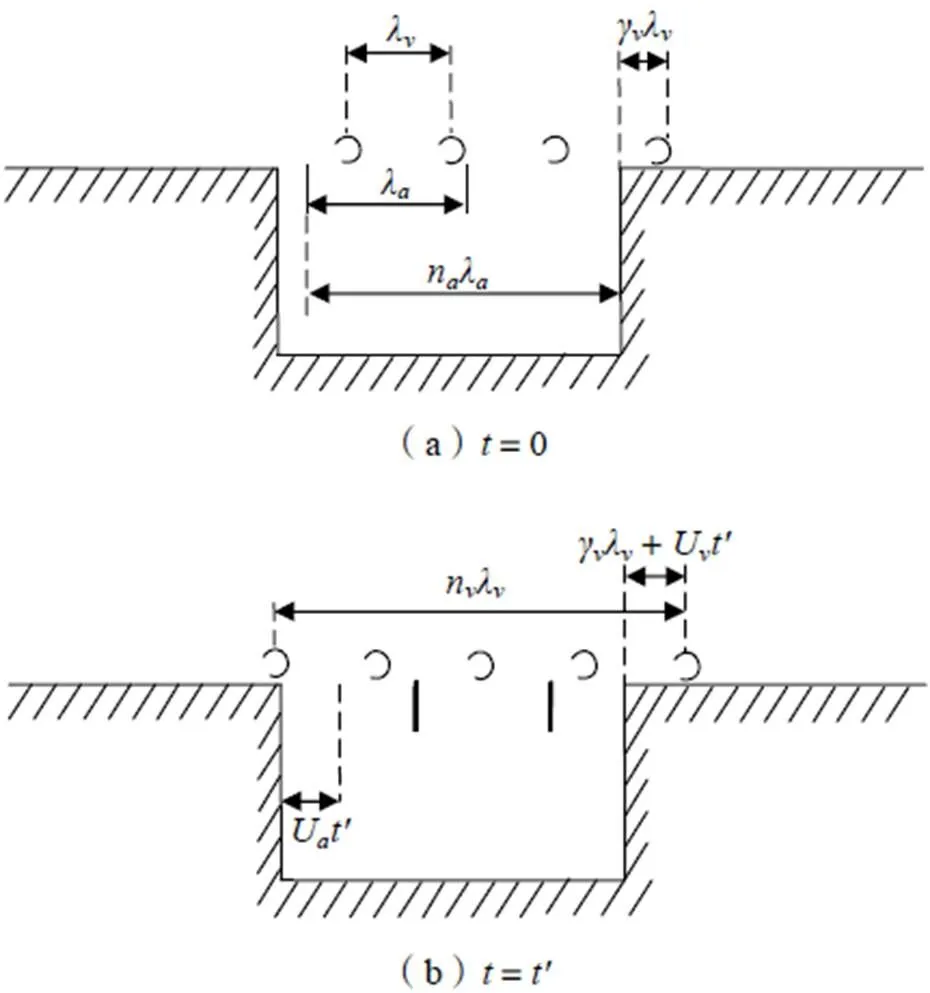
圖1 Rossiter渦脫分析示意圖[3]
結合式(1)~(3)可得:
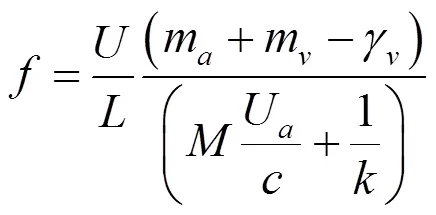
令:
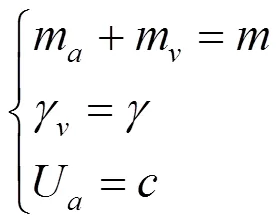
式(4)即可化為Rossiter公式:
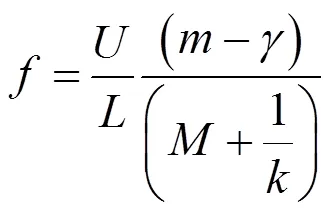
式中:為自由來流速度,m/s;為腔體流向長度,m;為模態階數;常數為相位延遲系數;為湍流運動速度與自由來流速度之比;為馬赫數。
1.2 大渦模擬方法(LES)
LES是對湍流脈動的一種空間平均,通過采用某種濾波函數將大尺度的渦和小尺度的渦分開,對大尺度的渦直接進行Navier-Stokes方程的求解,小尺度的渦用模型來封閉,從而減小計算成本。對于過濾掉的小尺度渦,通過引入亞格子(SubGrid-Scale,SGS)模型附加應力項來體現其對大尺度渦的影響。
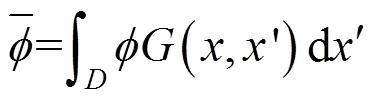
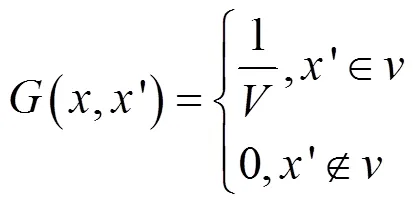
則:
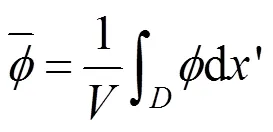
對Navier-Stokes方程進行濾波,則有:
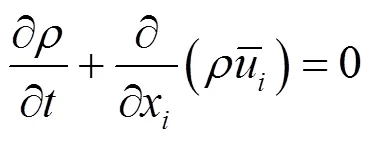
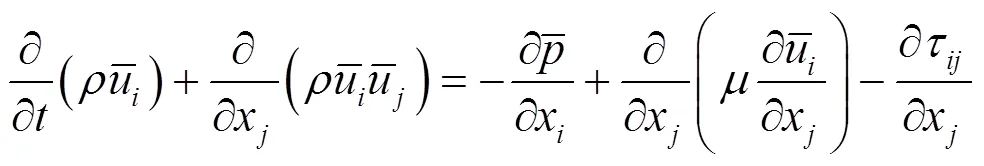
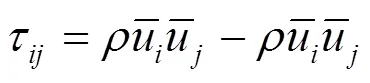
根據Smagorinsky的基本SGS模型,假定SGS應力具有下面的形式:
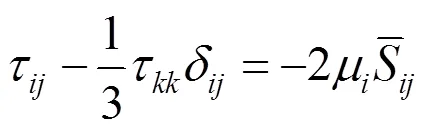

2 簡易腔體的建模
研究表明[11],腔體長深比小于1時,腔體剪切層自持續振蕩很容易與腔體自身的聲學模態發生耦合作用。為避免發生流體聲學作用而僅考慮流體動力學作用,本文腔體計算模型長寬比1.5:1。如圖2所示,腔體長900 mm、高600 mm。在腔體內部設置了1個監測點用來監測腔體內部脈動壓力的變化。為得到湍流渦運動速度,在腔體后緣中心線位置設置了一個湍流脈動壓力監測陣列用以進行波數-頻率譜分析,陣列由48個監測點組成,相鄰兩個監測點的間距為4.22 mm,如圖3所示。
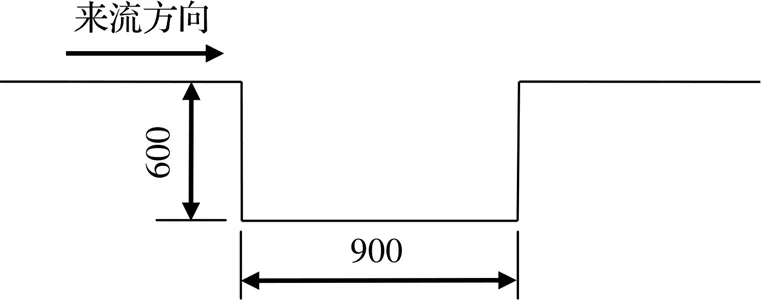
圖2 腔體幾何模型(單位:mm)
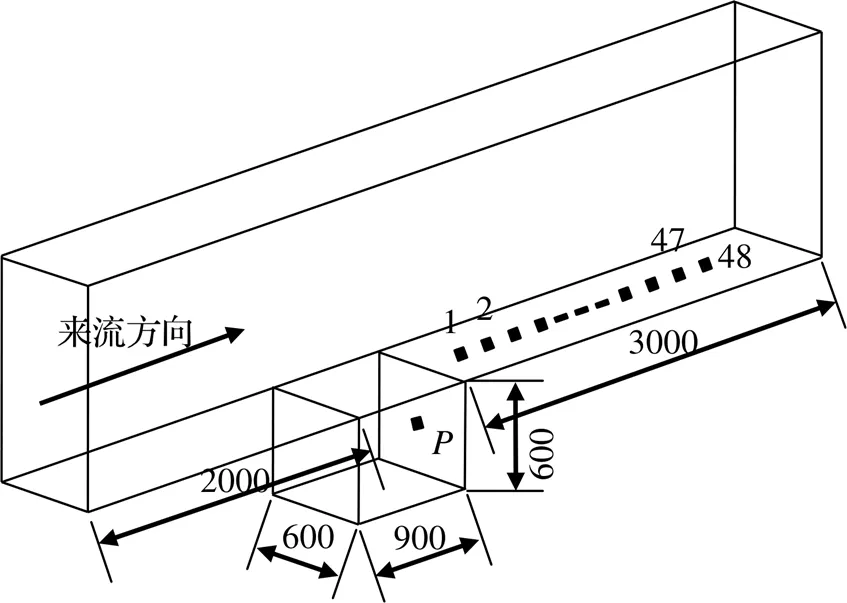
圖3 計算域與脈動壓力監測點(單位:mm)
如圖4所示,采用ICEM進行網格劃分,整個計算域采用非結構網格劃分,最大網格尺寸為70 mm,為了準確捕捉到腔體內部和附近的流場特征,對腔體附近流場區域采用網格加密處理,加密網格尺寸大小為15 mm,總網格數量在300萬左右。

圖4 腔體數值模擬網格劃分
進行數值計算時,考慮氣體的可壓縮性,將氣體屬性設置為理想氣體。計算域入口設置為質量氣流入口,出口設置為壓力出口。設置為先采用可實現的-兩方程模型進行穩態流場計算,計算結果作為瞬態計算的初始值。然后采用LES方法計算瞬態流場。瞬態時間步長可以直接確定空氣動力學噪聲的最大分析頻率,因此時間步長設置必須充分考慮研究的頻率范圍。根據Nyquist的采樣定理:要獲得原始信號而不會從采樣信號中丟失信號,采樣率必須至少是最大分析頻率的兩倍。由于腔體流致噪聲以中低頻為主,本文計算分析的最高頻率設定為=1000 Hz,為獲得更準確的計算結果,采樣率設置為2000 Hz。時間步長Δ=0.0005 s,迭代步數為20步,總采樣時間為1 s。
3 計算結果分析
3.1 腔體內部聲壓級
當自由來流速度為200 km/h,首先得到腔體內部監測點脈動壓力的時域數據,然后對其進行FFT(Fast Fourier Transform,快速傅立葉變換)變換得到腔體內部監測點的聲壓級頻譜,如圖5所示。
由圖5可看到,腔體內部測點位置存在三階峰值噪聲頻率,分別為27.3 Hz、62.5 Hz和99.6 Hz。故猜測最大渦脫落頻率為99.6 Hz,根據頻率與周期間的關系=1/,計算得到渦脫落最小周期為0.01 s。基于Q準則作出一個周期的渦圖,如圖6所示。
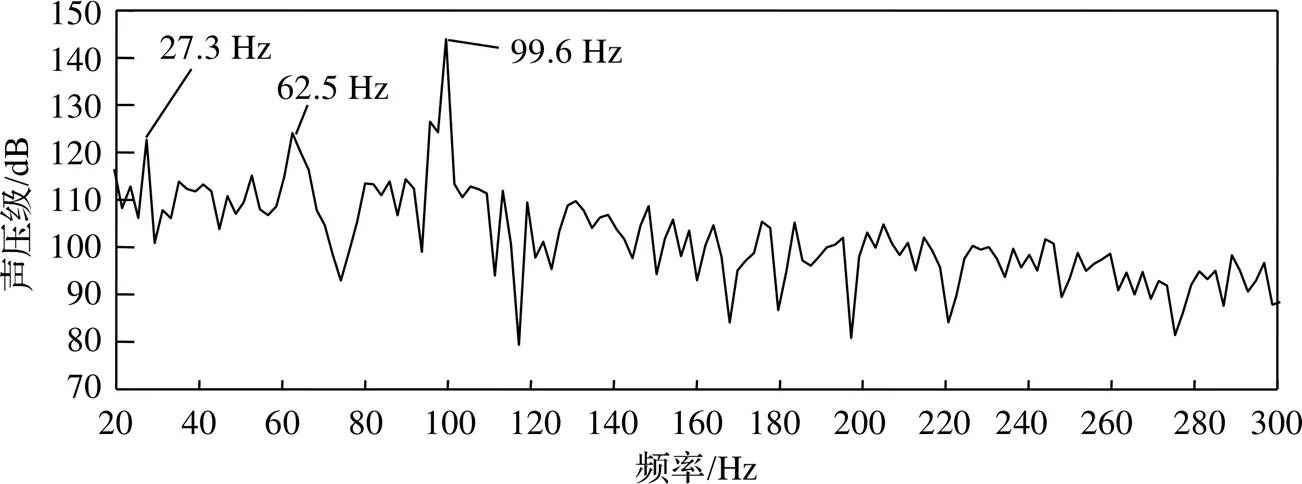
圖5 腔體內部監測點聲壓級頻譜
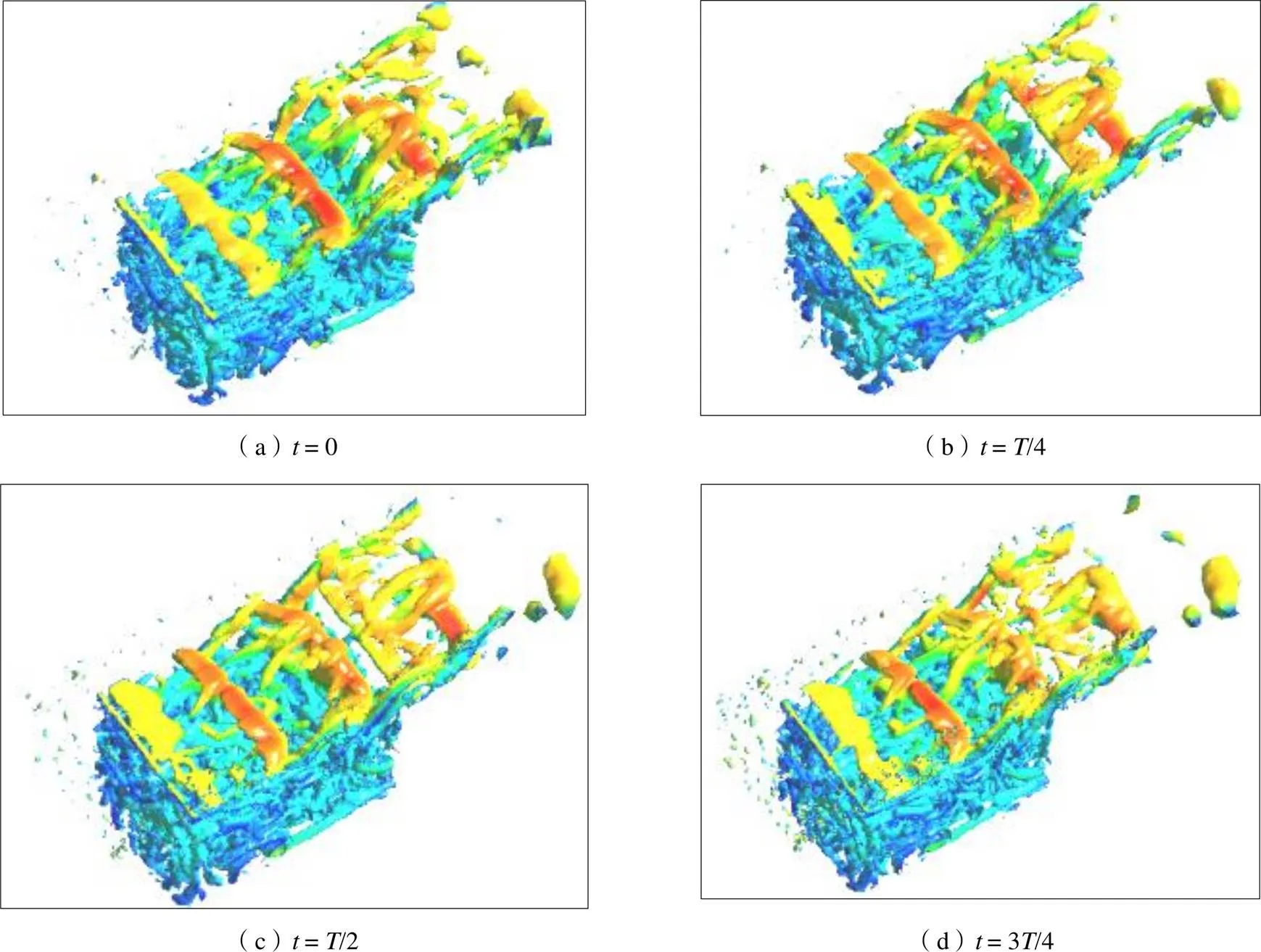
圖6 一個周期內的渦量圖
由圖6可看出,在整個周期內共有三個主渦:當=0時,第三個渦剛好撞擊到腔體后緣,腔體前緣新渦還沒有生成;當=/4時,第三個渦往腔體后緣運動,腔體前緣新渦逐漸生成;當=/2時,新渦已經生成并脫離腔體前緣,此時腔體上方重新有三個渦;當=3/4時,三個渦繼續向前運動,新的第三個渦接近腔體后緣;當=時,新的第三個渦撞擊到腔體后緣,新的一個周期開始。對于這一現象Rossiter認為流體流過腔體開口時的周期性渦脫落是邊緣音現象的特征,并且渦脫落和聲音輻射之間存在某些關系。聲輻射會導致渦流脫落,而渦向后運動撞擊到后緣會導致聲輻射,從而形成一個聲渦反饋現象。正是基于以上假設,他通過將自由剪切層簡化為離散渦模型推導出以后一直被廣泛采用的Rossiter半經驗預測公式。
由于在一個周期內腔體開口上方共有三個主渦,則Rossiter周期性渦脫落公式中=1、2、3時,代入腔體幾何數據和自由來流速度,取=0.57、=0.25計算得渦脫頻率,與大渦模擬結果對比如表1所示。
一般認為,相對誤差小于5%在工程可接受的范圍內,由表1可看出,預測頻率與數值模擬結果還有一定誤差,需更精確地確定值。
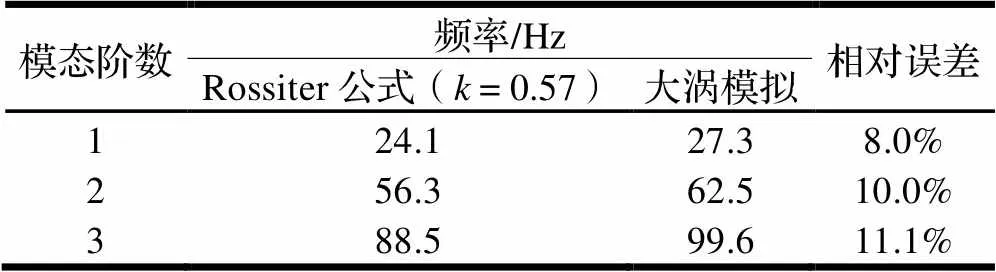
表1 峰值模態頻率對比
3.2 湍流脈動壓力的波數-頻率譜分析
波數-頻率譜分析法是波動分析法中的一種新方法,這種方法主要是把空間時間域信號變換到頻率波數域,進而通過對波數頻率譜的分析得到波傳播的信息。近年來,該方法在地震工程、電子通訊等方面有廣泛的應用。目前在振動噪聲方面的應用也逐漸增多。
表面壓力波動的波數-頻率圖可以從時空表面壓力的二維傅里葉變換獲得。它顯示了波數-頻域中特定波分量的大小在波數和頻率上的分布,進而得到該波動的傳播速度和傳播方向。二維傅立葉表達式為:
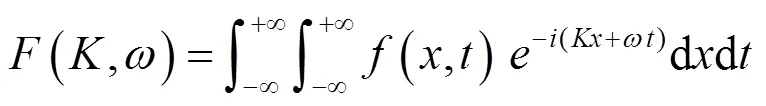
在實際中,由于測量的空間和時間有限,為了得到湍流脈動壓力作用下聲壓的波數頻率譜,一般通過對脈動壓力離散的時空信號進行離散的二維傅里葉變換,表達式為:
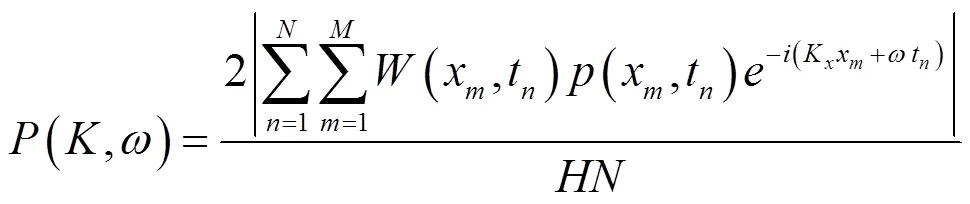
式中:為時間結點數;為空間脈動壓力監測點數;(x)和(t)均為窗函數,本文采用漢寧窗;為監測點的脈動壓力,Pa。
下面通過分析湍流脈動壓力的波數頻率譜來確定值。通過前面對Rossiter公式的推導知道,只需確定湍流運動速度即可確定值。
對腔體后緣中心線的湍流脈動壓力監測陣列進行二維傅里葉變換,得到湍流脈動壓力作用下聲壓的波數-頻率譜,如圖7所示。基于波的傳播速度不同,波數-頻率譜可將脈動壓力分為可壓縮部分和不可壓縮部分:當波的傳播速度小于聲速時,可認為是由于湍流渦直接作用到壁面產生的脈動壓力;當波數大于等于聲速時,可認為是由于聲傳遞時聲壓引起的。

圖7 腔體后緣壁面脈動壓力波數-頻率譜
由圖7(a)可看出,存在一條脊,該脊即為波數-頻率譜的湍流遷移脊,是由于湍流運動過程直接作用到后緣表面形成的。另外可以看到,湍流大部分能量都集中在遷移脊上,且主要在400 Hz以下,在100 Hz以下最為顯著,這符合湍流噪聲以低頻為主的特征。對脈動壓力監測陣列時間序列進行FFT變換,可得到各個監測點脈動壓力在頻域內的信息;對脈動壓力監測點陣列各個時刻空間序列進行FFT變換,可得到各個監測點脈動壓力在波數域的信息。結合波數和頻率的關系即可得到湍流運動時的傳播速度。
由圖7(b)可算出遷移脊的斜率Δ/Δ=5.56,根據:

自由來流速度為200 km/h,即為55.6 m/s,則湍流渦運動速度與自由來流運動速度之比為=0.63。將代入式(6),計算得前3階峰值噪聲頻率,與數值模擬結果對比如表2所示。
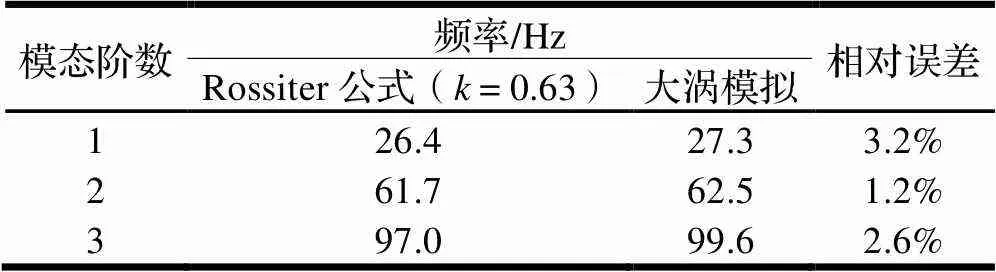
表2 峰值模態頻率對比
對比表2與表1可看出,當取0.63時,相比于取經典值0.57代入Rossiter公式預測效果更好。因為湍流運動速度受到湍流邊界層厚和腔體開口長度影響,即不同工況下湍流運動速度與自由來流速度之比不同。因此可以通過分析湍流脈動壓力的波數-頻率譜來計算湍流運動速度,確定Rossiter公式中的值,從而提高Rossiter公式的預測準確性。
4 結論
本文采用大渦模擬的方法,對腔體流動現象進行了數值模擬分析。首先確定了腔體流動自持續振蕩噪聲峰值頻率,并對腔體上方流動現象進行了詳細對比分析,然后構建并分析了腔體后緣脈動壓力作用下聲壓的波數-頻率譜,基于波數和頻率的關系得到了湍流運動速度,進一步得到了湍流運動速度和自由來流速度之比。主要結論如下:
(1)腔體流動過程存在自持續振蕩現象,并會產生特定頻率的噪聲峰值。
(2)可以通過分析腔體后緣湍流脈動壓力的波數-頻率譜得到湍流的運動速度,進一步得到湍流運動速度與自由來流速度之比,以提高Rossiter公式的預測準確性。
[1]Rockweel D,Naudascher E. Review—self-sustaining oscillations of flow past cavities[J]. Journal of Fluids Engineering,1978(100):152-164.
[2]李輝,肖新標,朱旻昊,等. 高速列車車廂連接處氣動噪聲特性初探[J]. 振動與沖擊,2016,35(6):109-114.
[3]Rossiter J. E. Wind-tunnel experiments on the ?ow over rectangular cavities at subsonic and transonic speeds[R]. Aeronautical Research Council Reports and Memoranda,October,1964:1-32.
[4]EAST L F. Aerodynamically induced resonance in rectangular cavities[J]. Journal of Sound and Vibration,1966,3(3):277-287.
[5]MA R,SLABOCH P E,MORRIS S C. Fluid mechanics of the flow-excited Helmholtz resonator[J]. Journal of Fluid Mechanics,2009(623):1-26.
[6]董小杏. 基于CFD除霜風道結構分析及優化設計[J]. 機械,2018,45(12):26-28,32.
[7]Comte P,Daude F,Mary I. Simulation of the reduction of unsteadiness in a passively controlled transonic cavity ?ow[J]. Fluids Struct,2008,24(8):1252-1261.
[8]楊國晶. 陷落式腔體水動力特性研究[D]. 哈爾濱:哈爾濱工程大學,2009.
[9]Li W,Nonomura T,Fuji K. On the feedback mechanism in supersonic cavity flows[J]. Physics of Fluids,2013,25(5):2118-2128.
[10]鄧玉清,張楠. 孔腔脈動壓力及其波數-頻率譜的大渦模擬研究[J]. 船舶力學,2017,21(10):1199-1209.
[11]East L F. Aerodynamically induced resonance in rectangular cavities[J]. Journal of Sound and Vibration,1966,3(3):277-287.
The Frequency of Self-Sustained Oscillation of Cavity Flow Based on Wavenumber-Frequency Spectrum
NI Xiaosong,XIAO Xinbiao,LIU Haonan
( State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China )
In the semi-empirical Rossiter formula, which is currently generally recognized and widely used in self-sustained oscillation of cavity flow noise frequency prediction, only the recommended value of the empirical constantis given, and no specific calculation method is given. Therefore, this paper uses numerical simulation to determine the value of. First, the LES turbulence model is used to establish the cavity self-sustained oscillation noise prediction model. Furthermore, the first three-order noise peak frequency is obtained by analyzing the monitoring points inside the cavity and compared with the predicted frequency of Rossiter formula with the recommended value of(0.57). The predicted results have certain deviation. Then, by analyzing the wavenumber-frequency spectrum of the turbulent pulsating pressure at the trailing edge of the cavity, thevalue of 0.63 is obtained and substituted into the Rossiter formula. The first three-order noise peak frequency is obtained, which is in good agreement with the numerical simulation results. The results show that it is feasible to determine the empirical constantby analyzing the wavenumber-frequency spectrum of the turbulent pulsating pressure, and it can improve the accuracy of the Rossiter formula to predict the frequency.
cavity flow induced noise;peak frequency;Rossiter formula;wavenumber-frequency spectrum
TB123
A
10.3969/j.issn.1006-0316.2021.09.001
1006-0316 (2021) 09-0001-07
2021-01-21
國家自然科學基金(U1934203)
倪小松(1996-),男,湖南衡陽人,碩士研究生,主要研究方向為軌道交通減振降噪,E-mail:1512015956@qq.com。
通訊作者:肖新標(1978-),男,廣東陽春人,博士,副研究員,主要研究方向為軌道交通減振降噪,E-mail:xinbiaoxiao@163.com。

