中小跨徑簡支T形梁橋的設計參數分析

楊芬,張華

摘 要：為了提高中小跨徑簡支T形梁橋建設水平，首先歸納總結了簡支T形梁橋設計荷載類型和技術設計參數、經濟設計參數的內容，隨后提出了T形截面梁極限承載力、鋼含量、樁基參數的計算方法，最后分析了配筋率、梁高、跨徑之間的函數關系，研究成果可為類似的簡支T形梁橋的設計與施工提供科學的理論指導。

關鍵詞：中小跨徑;簡支T形;設計參數;設計方法;變化趨勢

0 引言

隨著基礎交通設施網絡的完善，公路工程建設規模持續擴大，同時為了跨越各種障礙物，應當布置各種類型的橋梁。根據相關部門的統計數據可知，中小跨徑在橋梁工程所占的比重較大。簡支T形梁橋由于自重低、適應性強、截面受力合理等，已經發展成國內中小跨徑橋梁建設重要橋型。但是由于原有簡支T形梁橋設計理念落后，設計參數計算理論不完善等原因，使得橋梁在運營期間出現各種病害，嚴重影響了行車安全和橋梁運營壽命，造成不良的社會影響。同時工程人員在開展簡支T形梁橋建設時，仍以工程類比法為主，設計方案偏保守 [1]。因此，分析中小跨徑簡支T形梁橋的設計參數分析具有十分重要工程意義。

1 簡支T形梁橋設計荷載和設計參數

1.1 簡支T形梁橋設計荷載

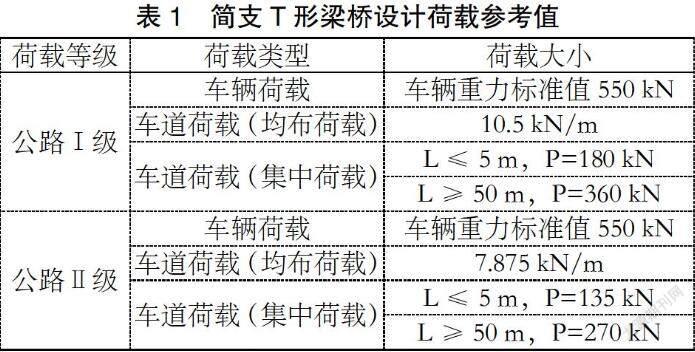
簡支T形梁橋的設計是基于“公路橋梁可靠度理論”，該理論把影響T形梁橋安全性和耐久性的各種因素當作隨機變量，并利用統計數學原理來建立各變量間的函數關系，以計算橋梁結構的可靠度。同時，簡支T形梁橋可靠度設計有兩種狀態（承載極限狀態和正常使用極限狀態進行設計），而這兩種狀態的可靠度計算都必須選擇合適的設計荷載。根據《公路橋涵設計通用規范》（JTG D60—2015）可知，簡支T形梁橋的設計荷載等級包括公路Ⅰ級和公路Ⅱ級，各荷載等級下荷載大小如表1所示[2]：

1.2 簡支T形梁橋設計參數

簡支T形梁橋結構設計中的核心任務是設計參數選擇和計算。橋梁結構的設計可能存在多個相互聯系的設計參數，各參數的隨機組合會直接影響設計方案的選擇，但是沒有必要把所有影響橋梁結構設計結果的因素都當做設計參數來計算，而是應當堅持重視主要因素、忽略次要因素的原則來選擇設計參數。簡支T形梁橋結構的設計參數通常有技術參數與經濟參數方面[3]。

1.2.1 技術參數

工程中常用的簡支T形梁橋結構主要有鋼筋混凝土結構與預應力混凝土橋梁結構，這兩種橋梁結構材料均由鋼筋、混凝土[4]。因此，在進行簡支T形梁橋結構時必須要確保橋梁的安全性、耐久性、適用性等，所選擇的車輛荷載、橋梁跨徑、截面尺寸、鋼筋直徑及配筋率等也要符合相應的規范要求。根據相關研究成果可知，配筋率、含鋼量（單位體積混凝土鋼筋重量）可作為評價簡支T形梁橋性能的關鍵技術指標。此外，如果簡支T形梁橋采用樁基礎，樁基承載力、樁基數量等也是重要的設計參數。

1.2.2 經濟參數

簡支T形梁橋結構建設期間，其工程造價主要源于施工原材料成本（比如混凝土用量、鋼筋用量及市場價格）、后期維修養護費用、建設資金利息等。鑒于此，T形梁橋結構中的含鋼量也可作為評價其設計水平的經濟指標。

2 簡支T形梁橋設計參數計算

2.1 T形截面梁極限承載力分析

簡支T形梁橋結構的極限承載能力與矩形截面橋梁的分析方法基本一致，即T型截面在計算時只考慮其在荷載作用下的受壓破壞和下邊緣的受拉破壞，計算公式如下[5]：

式中：、分別是縱向普通鋼筋和預應力鋼筋的抗拉強度，kPa;、分別是縱向普通鋼筋和預應力鋼筋的截面面積，mm2; 橋梁混凝土抗壓強度，kPa;是T型梁截面寬度，m;是T型梁截面高度，m，以上參數均為設計值。

2.2 鋼含量參數

鋼筋是簡支T形梁橋結構的骨架，配筋率大小會直接影響到橋梁結構的承載能力。為了提高簡支T形梁橋結構設計的合理性，其鋼含量必須控制在合理的范圍內，不得小于最小配筋率，也不能超過最大配筋率。如果鋼含量較少，會導致橋梁結構的承載力不足或截面過大，影響橋梁結構設計的經濟性;如果鋼含量較多，會使得橋梁結構設計偏于保守，造成一定的資源浪費。但是，國內外學者和工程人員在研究簡支T形梁橋結構鋼含量時主要是基于統計數據，針對理論層面的研究較少。筆者結合多年工程實踐經驗，提出一種鋼含量計算方法如下：

式中：—含鋼量，kg/m3;—橋梁結構中鋼筋重量，kg;—橋梁結構混凝土體積，m3。

2.3 樁基礎設計參數

2.3.1 樁基極限承載力

簡支T形梁橋結構的樁基礎在計算其承載力時，往往只計算樁底反力，而對嵌巖段側摩擦阻力不予考慮，僅視為安全系數儲備。同時，樁基安全系數的確定應綜合考慮巖體均勻性、裂隙發育情況等因素，通常取2.5～3.0，其中堅硬、裂隙少的巖體安全系數取小值，中風化或強風化、裂隙發育程度高的巖體安全系數取大值[6]。

2.3.2 樁基數量

簡支T形梁橋結構的樁基數量n可根據其承載力計算結果來初步估算，如下式：

式中：—樁基豎向力，kN;—承臺及承臺以上土的重力，kN;—單樁承載力，kN。

如果樁基礎處于偏心受壓狀態，且群樁截面形心和荷載合力作用點基本重合，可按上式初步擬定樁基根數，然后進行樁基受力驗算。如果群樁截面形心和荷載合力作用點距離相差較大，可將上述樁基根數提高10%～20%。

3 簡支T形梁橋設計參數之間的關系分析

3.1 工況選擇

筆者以某鋼筋混凝土簡支T形梁橋工程位研究對象，分析了不同工況下梁高、跨徑等與配筋率之間的關系，并對各參數間的關系進行了數學擬合，其中梁高分別取0.7 m、0.8 m、0.9 m、1 m、1.1 m、1.2 m，荷載工況取5中，分別如下：工況1去自重，工況2取自重+汽車Ⅱ級荷載（雙車道）、工況3取自重+汽車Ⅰ級荷載（雙車道）、工況4取自重+汽車Ⅰ級荷載（三車道）、工況5取自重+汽車Ⅰ級荷載（四車道）。

3.2 荷載、梁高與配筋率關系

簡支T形梁橋結構的配筋率與荷載的關系如圖1所示：

圖1表明：在簡支T形梁橋梁高不變的條件下，隨著荷載的增加，不同工況下橋梁結構配筋率也逐漸提高，且兩者基本呈線性正相關關系。如果橋梁荷載保持固定，則不同梁高下簡支T形梁橋的配筋率會隨著梁高的增加而降低，但此時配筋率降低速率并不是固定的。當梁高小于1 m時，梁高每提高0.1 m，簡支T形梁橋配筋率減小速率逐漸變緩;當梁高大于1 m時，簡支T形梁橋配筋率隨梁高的減小速率基本保持不變。

3.3 梁高與跨徑關系

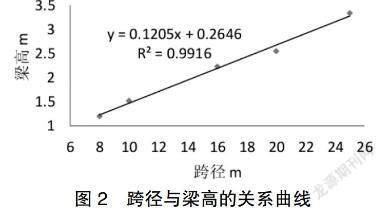
由鋼筋混凝土的受力特性可知，T型梁橋的跨徑不宜過大，常用跨徑在8 m～24 m。當T型梁橋跨徑超過20 m，梁高可能增長過快，使得梁體結構受力不合理，故筆者對8 m、10 m、16 m、20 m、24 m跨徑的橋梁梁高進行計算，計算結果見圖2：

圖2表明：隨著T型梁橋的跨徑增加，其梁高也不斷增加，且兩者之間基本呈線性正相關關系。同時，梁高與跨徑的函數關系可表示Y=0.120 5X+0.264 6，相關系數R平方=0.991 6，兩設計參數間的相關性較好，在工程允許誤差范圍內。

又計算結果可知，T型梁橋的跨徑為8 m、10 m、16 m、20 m時，其對應的推薦梁高分別為 0.8 m、0.9 m、1.3 m、1.5 m，高跨比基本保持在 1/10～1/15 左右。如果T型梁橋跨徑不受橋下凈空的影響，應當適當增大梁高，以改善橋梁結構應力分布，提高其正截面承載性能，減小鋼筋用量。但是梁高增加幅度也不能過大，否則其配筋率可能超過最大配筋率要求。

4 結語

本文分析了簡支T型梁橋的設計荷載、設計參數及各參數的計算方法和相互聯系，主要得到了以下結論：（1）簡支T形梁橋設計是基于公路橋梁可靠度理論，包括承載極限狀態和正常使用極限狀態設計。（2）簡支T形梁橋結構存在多個相互聯系的設計參數，可劃分成技術參數與經濟參數兩方面。（3）簡支T形梁橋技術參數有配筋率、含鋼量、樁基承載力、樁基數量等，經濟參數有原材料價格、維修養護費用、建設資金利息等。（4）簡支T形梁橋的配筋率、跨徑與梁高基本呈線性正相關關系，在設計時如可適當增大梁高來提高其正截面承載性能，減小鋼筋用量。

參考文獻：

[1]周青，傅晨曦，韓大章.中小跨徑鋼混組合梁橋設計標準化關鍵參數研究[J].上海公路，2020（1）：43-49.

[2]石雪飛，許琪.遼寧省中小跨徑鋼混組合結構橋梁全壽命周期成本分析[J].北方交通，2019（2）：5-8.

[3]王克海，魯冠亞，張盼盼.基于機器學習的中小跨徑公路梁橋抗震設計評價方法研究[J].公路交通科技，2019，36（2）：74-84.

[4]馬赟.中小跨徑簡支T形梁橋設計參數分析[D].長安大學，2014.

[5]西部地區在役中小跨徑橋梁承載力快速檢評技術研究[J].西部交通科技，2014（1）：1-6+14.

[6]李耘宇.FRP/鋼—混凝土組合簡支梁橋試驗、分析與設計方法[D].大連理工大學，2016.