基于“三個理解”挖掘內隱性課程資源

殷玲 蔣孝國

摘? 要：“三個理解”和內隱性課程資源中均蘊含了數學、學生和教學等方面的內容. 將兩者結合，相互印證，并結合教學案例具體闡述如何在新授課教學中從理解數學、理解學生、理解教學的角度創設適切的問題情境，挖掘和整合內隱性課程資源，促進學生深度學習.

關鍵詞：理解數學;理解學生;理解教學;內隱性課程資源

新一輪高中課程改革以促進學生的終身發展為本，以提升學生的學科核心素養為目標，而挖掘與整合數學內隱性課程資源，促進學生深度學習，是落實數學學科核心素養的有效途徑之一. 內隱性數學課程資源主要包括內隱素材性資源（即數學知識的背景、過程、環境及文化元素等）和內隱條件性資源（即教師的教學知識，學生原有的認知情況，合適的教學手段，方法和環境等）. 結合章建躍博士提出的“三個理解”——理解數學、理解學生、理解教學，不難發現內隱性課程資源中也蘊含了對數學、學生和教學等方面的要求. 因此，筆者認為，基于“三個理解”，可探索、挖掘與整合內隱性課程資源，以優化教學，提升學生的數學學科核心素養. 本文著眼于新授課教學，輔以案例，借助適切的問題情境具體闡述，與大家交流.

一、基于理解數學，構建知識生長點，挖掘知識形成過程中的資源

數學概念是不斷抽象的結果. 例如，函數作為中學數學的核心概念，歷經初中和高中兩個階段，從“變量說”過渡到“對應說”;又如，在教學“平面和平面垂直”時，為了引入面面垂直的判定定理，需要先學習二面角的知識. 但是對于學生而言，二面角是個全新的概念. 在教學中教師要幫助學生實現從具體到抽象、從感性到理性的過渡，從而完成概念的構建.

案例1：平面和平面垂直（1）.

導入語：大家會折紙么？一張薄薄的紙，經一雙巧手，翻、折、疊、拉等，可以呈現很多精美的造型. 今天，我們利用折紙，一起來發現生活中有趣的數學問題. 取一張正方形紙，進行一次對折. 經過對折，可以得到如圖1所示的兩個立體圖形. 它們都有兩個平面和一條公共棱. 你能從生活中找到類似的模型嗎？

打開的筆記本電腦、翻開的書、教學樓的屋頂……，教師指明這樣的立體模型有很多，是今天要學習的二面角.

問題1：如何定義二面角？

師生活動：學生獨立思考，教師引導學生類比平面中的角來定義二面角.

追問1：平面中角的定義是什么？

從平面內一點引發兩條射線所組成的圖形叫做角.

追問2：大家仔細觀察折紙模型，將維度升級，給二面角下個定義.

從一條直線引發的兩個半平面所組成的圖形叫二面角.

追問3：仿照平面幾何中角的記法[∠AOB，] 二面角怎么表示？

問題2：在折紙的過程中，可以發現二面角張開的程度不同，如何刻畫？

師生活動：學生思考后，討論、回答：可以通過平面角刻畫二面角的大小. 教師鼓勵學生在模型上畫出符合條件的平面角，并分組討論操作的可行性，體驗二面角平面角的存在性和唯一性. 二面角大小的度量是本節課的重點，也是難點，教師參與討論，給予指導，并讓學生展示討論結果.

【評析】教師利用折紙這個簡單易行的活動，有意識地引領學生進行實踐操作，直觀感知立體圖形，借助類比和轉化，得出二面角的定義、表示、度量，既能鍛煉學生的動手能力、團隊協作能力，還能使學生體會到數學活動的科學性和嚴謹性.

理解數學指教師清楚數學知識的產生背景、形成過程和方法，把握數學知識的邏輯體系、結構和與相關知識的聯系. 本案例將生活與數學相結合，利用折紙活動吸引學生參與到實踐操作中來，通過折一折、畫一畫、想一想，直觀感知二面角，這是從生活中建構數學知識的生長點，讓學生親歷數學知識的形成過程. 可見，基于理解數學，可以挖掘知識形成過程中的資源，通過學生體驗性活動，讓學生形成伴隨學習活動過程的體驗性知識（包括對知識產生、發展、結果、應用的體驗）等，從而激發學生進一步理解數學知識，形成良性循環，促進學生深度學習.

二、基于理解學生，立足學生薄弱點，挖掘符合學生認知的資源

數學教學的對象是學生，教學的起始點應基于學情. 因此，理解學生、掌握學情是進行教學設計和實施教學的重要基礎. 為了幫助學生提高思維品質，需要教師在教學設計時采用符合學生認知結構的方式，從學生的角度出發，立足學生的薄弱點，引發思考，探究數學知識.

案例2：共面向量定理.

導入語：一個數學概念的推廣會帶來更好的性質與應用，學生能夠從中體驗數學在結構上的和諧性，感悟由此產生的影響. 為了解決平面上有關點、直線的位置關系和度量問題，我們引進了平面向量及其運算. 上節課我們進一步擴大視野，將向量由平面向空間推廣，建立相應的運算，今天我們繼續研究空間向量的有關性質.

觀察如圖2所示的長方體，回答下列問題.

（1）你能找出一個與[AC]共線的向量嗎？

（2）你能用[AB， AD]表示出[AC]嗎？

（3）[AB， AD， A1C1]具有怎樣的關系？

師生活動：學生思考后回答，教師引導學生直觀感知共面向量，并提出問題.

問題1：類比共線向量的定義，你能給出共面向量的定義嗎？

追問：空間中任意兩個向量是共面向量嗎？任意三個向量共面嗎？

問題2：平面向量中，向量[b]與非零向量[a]共線的充要條件是[b=λa，] 類比到空間向量，若[p]與兩個不共線向量[a，b]共面，那么它們之間存在怎樣的關系？

師生活動：學生思考，教師引導學生回顧平面向量基本定理，得出存在有序實數組[x，y，] 使得[p=][xa+yb.]

追問：對于空間中的三個向量[p，a，b]（[a]與[b]不共線），若存在有序實數組[x，y]使[p=xa+yb，] 那么向量[p，a，b]共面嗎？

【評析】此案例源于筆者參加的一次區評優課，借班上課的學生數學基礎比較薄弱，因此教師基于學情，利用長方體這一基本模型，設置針對性較強的問題，引入概念. 第（1）小題復習共線向量定理;第（2）小題復習平面向量基本定理;第（3）小題引出共面向量的概念. 問題設置均在學生思維的最近發展區，起點低但有梯度，拾級而上，符合學生的認知特點;教師適時追問，引導學生深度思考任意三個向量是否共面，何時共面，自然引入本節課的主題——探究共面向量定理. 在共面向量定理探究環節，必要性通過回顧平面向量基本定理就可解決，充分性則類比共面向量的作圖進行驗證，教學先易后難、循序漸進.

理解學生，即認識學生數學學習的思維特征和認知規律，了解學生的知識儲備、能力基礎和學習數學難點知識的思維障礙等. 挖掘內隱性課程資源，也需要考慮學生的思維水平，建構緊扣教學目標的、有的放矢的問題情境. 作為課堂的主體，學生的積極性和求知欲直接影響教學效率，案例充分考慮學生學情，挖掘符合學生認知的資源，從共線向量、平面基本向量入手，設置有階梯且目標明確的問題驅動課堂，幫助學生理清知識的邏輯關系，實現知識的遷移. 當然，從理解學生的角度挖掘內隱性課程資源，還可以關注學生的興趣點、困惑點、頓悟點，挖掘課堂生成的意外點等資源，促進學生多維思考，發展數學抽象、邏輯推理等數學學科核心素養.

三、基于理解教學，把握教材重、難點，挖掘優化教學方法的資源

希伯特將教學描述為“在課堂中圍繞內容，并促進學習目標達成的師生、生生活動”. 教學的任務是創造一個學生參與的環境來引發學生的思考，而不是直接將知識或方法灌輸給學生. 在一次公開課教學中，筆者聽了一節青年教師的新授課，教學流程如下.

案例3：拋物線的性質.

師：上節課中，我們學習了拋物線的標準方程，本節課我們來研究拋物線的幾何性質.

下面我們來學以致用，完成例題.

……

在不到5分鐘的性質歸納之后，就是滿滿的課堂例題講解.

誠然，在這位教師看來，填寫表格對學生而言沒有什么難度，所以教學的側重點是例題的講解，即拋物線性質的應用. 其實不然，弗賴登塔爾認為，學習數學唯一正確的方法是實現再創造，也就是通過學生自己的做數學活動，把本來需要教師傳授的知識、需要浸潤的觀念變為學生在活動中自主生成、緘默感受的東西，這是一種自然、有效的學習方法. 因此，本課時教師的任務并不是將現成的結論灌輸給學生，而是引導和幫助學生進行再創造的活動，即讓學生參照橢圓或雙曲線的幾何性質的學習經驗對拋物線的性質進行獨立探索.

筆者在與執教教師交流溝通后，創設問題情境如下.

導入語：生活中處處有拋物線的身影，噴泉、拱橋、彩虹……就連大家喜歡的小游戲“憤怒的小鳥”中也存在拋物線的身影，想知道小鳥能否擊中小豬，就需要研究拋物線的有關性質.

問題1：前面我們學習了橢圓和雙曲線的幾何性質，如何探究拋物線的性質？

師生活動：學生思考后回答“通過類比橢圓的性質探究了雙曲線的性質，可以嘗試類比橢圓的性質探究拋物線的性質”. 教師給予鼓勵，并指明類比不僅是形式上的類比，也可以是探究方法和思維方式的類比.

問題2：以焦點在[x]軸上的橢圓為例，回憶橢圓性質的探究過程.

師生活動：學生回答并相互補充，完成對橢圓性質的復習，包括范圍、頂點、對稱性等. 教師適時追問.

追問1：如何得到[x]和[y]的取值范圍？

通過觀察幾何圖形和從代數角度計算可得.

追問2：如何得到頂點和對稱性？

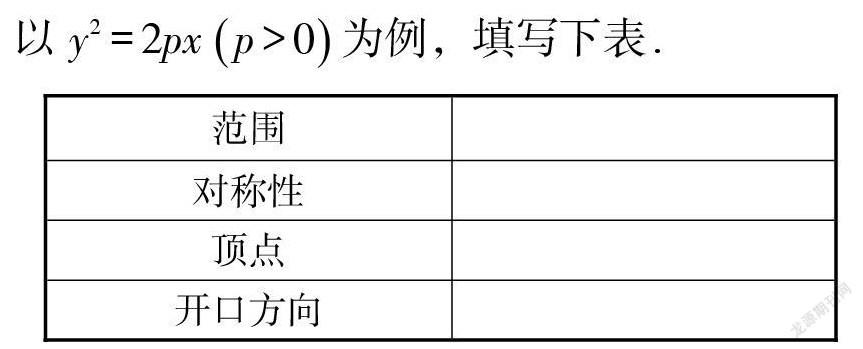
問題3：以[y2=2px p>0]為例，從幾何和代數兩個角度探究拋物線的性質.

【評析】通過充滿趣味的小游戲創設問題情境，激發學生的學習興趣. 在教學中著重滲透類比思想，抓住本節課學習的重點，即類比橢圓的性質研究拋物線的性質，鍛煉學生的歸納和推理能力. 特別地，在研究變量范圍、頂點、對稱性的時候，要多問學生幾個“為什么”，讓學生不僅能從幾何圖形直觀感知拋物線的性質，還要理解圓錐曲線幾何性質的研究過程——幾何性質代數化，形成用解析法研究幾何問題的經驗系統，促進學生深度理解[x，y]的代數特征和幾何意義，進行有效的思維固著.

理解教學，是指教師清楚教學的本質與功能，掌握一定的教學方法和教學藝術，清楚學生的認知規律和教學的基本原則，能夠把教與學作為有機的、統一的、相互促進的整體來處理.

例如，案例3中教學不應該滿堂灌例題，而應該引導學生先對拋物線的性質進行本質探究，從而進一步掌握用解析法來研究解析幾何，提升學生自主解決一般問題的能力. 基于理解教學，教師需要精心研究教材與教法，熟悉教學的重、難點，優化教學方法，可以根據對內隱性課程資源中素材性課程資源的理解，結合外顯條件性資源，構建適合學生共同參與學習的課堂環境，通過不斷追問、質疑、反思等途徑，幫助學生歸納學習方法，促進學生深層次思考，積累基本活動經驗.

理解數學、理解學生、理解教學是實施有效教學的根本保證. 基于“三個理解”，可以化隱性資源為顯性資源，并為挖掘內隱性課程資源提供思路和一般方法，構建促進學生深度學習的優質環境，促進學生理解力、思考力、應用力和創新力持續發展.

參考文獻：

[1]章建躍. 中學數學課改的十個論題[J]. 中學數學教學參考（中旬），2010（3）：2-5，11.

[2]喻平. 論內隱性數學課程資源[J]. 中國教育學刊，2013（7）：59-63.

[3]華志遠. 發掘內隱性課程資源? 促進學生深度學習[J]. 中學數學雜志，2019（5）：8-10.