讓傳統(tǒng)板書成為激發(fā)數(shù)學思維的支架

陳算榮 董琳琳 陳建祥

摘? 要：在傳統(tǒng)板書逐漸被現(xiàn)代媒體板書取代的當下，有必要為其發(fā)聲. 等比數(shù)列前[n]項和公式是高中數(shù)學的重要公式之一，在引導學生探究等比數(shù)列前[n]項和公式的過程中，很多教師的處理浮于表面，沒有達到探尋方法實質(zhì)的效果，學生的思維并沒有得到主動發(fā)展. 抓住知識的本質(zhì)，巧妙利用傳統(tǒng)板書，可以有效引導學生進行類比思考，從而幫助學生主動發(fā)現(xiàn)錯位相減法，體驗探尋公式推導方法的過程.

關(guān)鍵詞：傳統(tǒng)板書;等比數(shù)列;數(shù)學思維;教學支架

一、引言

“等比數(shù)列前[n]項和”經(jīng)常出現(xiàn)在高中公開教學選題中，不僅因為等比數(shù)列前[n]項和公式是高中數(shù)學的一個重要公式，也因為其推導過程中蘊涵著類比、特殊到一般等數(shù)學思想方法，是培養(yǎng)學生數(shù)學運算和邏輯推理等素養(yǎng)的落地點. 然而，很多公開教學課在公式推導探究過程中出現(xiàn)“有形無實”的現(xiàn)象，忽略公式生成過程的教學，并沒有很好地發(fā)展學生的數(shù)學思維，體現(xiàn)和落實核心素養(yǎng).

在日常教學中，一些教師在引導學生探究等比數(shù)列前[n]項和公式的推導時，表面上讓學生類比等差數(shù)列前[n]項和公式的推導，但是對于類比什么、如何類比的處理不盡如人意. 學生在等比數(shù)列前[n]項和公式的推導過程中雖然能夠體會到倒序相加法行不通，但是尋找合適的方法的過程卻被教師的“替代思維”給淹沒了. 教師往往急于告知學生“是什么”，至于“怎么樣”和“為什么”學生不得而知. 因此，學生并沒有真實經(jīng)歷發(fā)現(xiàn)和理解錯位相減法的過程. 這樣的教學會導致學生死記硬背公式，而體會不到公式推導過程中的數(shù)學本質(zhì)和數(shù)學之美.

上述現(xiàn)象的出現(xiàn)和問題的存在，究其原因，主要有以下三個方面：（1）教師對公式推導方法的知識本質(zhì)分析不到位;（2）教師對啟發(fā)學生思考及落實核心素養(yǎng)的路徑不清晰;（3）很多教師在使用幻燈片等多媒體技術(shù)進行等比數(shù)列前[n]項和公式教學時，忽略了對傳統(tǒng)板書的價值開發(fā).

基于這些問題及診斷，我們開展了教學設計思考和教學實踐. 本文旨在通過呈現(xiàn)公式推導關(guān)鍵部分的教學實施片斷，以及相應的板書設計和使用，闡明如何在教學過程中抓住知識本質(zhì)，巧用傳統(tǒng)板書，引導學生思考和探索等比數(shù)列前[n]項和公式的推導方法，幫助學生把握錯位相減法的實質(zhì)，感悟數(shù)列求和過程中蘊涵的數(shù)學思想. 同時，讓學生充分感受等比數(shù)列前[n]項和公式表露出來的數(shù)學之美，加深學生的印象，營造高效的數(shù)學課堂.

二、教學實施片斷

課的開始，教師先給出問題情境：古印度的國王舍罕王打算重賞國際象棋的發(fā)明者宰相西薩·班·達依爾，問他想要得到什么賞賜. 這位宰相跪在國王面前說：“陛下，請您在國際象棋棋盤的第一個小格內(nèi)賞給我1粒麥子，在第二個小格內(nèi)賞給我2粒麥子，在第三個小格內(nèi)賞給我4粒麥子，依此類推，每一個小格內(nèi)的麥子數(shù)量都是前一個小格內(nèi)的麥子數(shù)量的2倍. 陛下啊，請把這樣擺滿棋盤上所有64格的麥粒，都賞給您的仆人吧！”國王能滿足宰相的要求嗎？

然后，教師引導學生從中提煉出要解決的數(shù)學問題：麥粒總數(shù)=[1+2+22+…+263]. 接著，教師引導學生表述：這是一個求以[1]為首項、[2]為公比的等比數(shù)列前[64]項和的問題. 由此引出本節(jié)課的課題.

下面是妙用板書促進學生思考和探索等比數(shù)列前[n]項和公式的教學過程.

1. 關(guān)聯(lián)舊知

教師提出：為了探索等比數(shù)列前[n]項和公式，我們不妨先來解決這個具體的數(shù)學問題. 如何求以[1]為首項、[2]為公比的等比數(shù)列前[64]項的和？

教師將這個具體數(shù)列求和的式子板書在主板書左側(cè)，編號為①.

教師在巡視過程中發(fā)現(xiàn)大部分學生借鑒等差數(shù)列求和的方法，運用倒序相加法得到等式[2Sn=263+1+][262+2+…+231+232]，但都無法繼續(xù)求解.

教師啟發(fā)：追本溯源，為什么等差數(shù)列可以用“倒序相加法”求和而等比數(shù)列卻不能？請同學們回到這兩類數(shù)列的定義進行思考.

經(jīng)過啟發(fā)，學生領(lǐng)悟到這兩類數(shù)列的本質(zhì)區(qū)別：等差數(shù)列是后一項與前一項的差為定值，等比數(shù)列則是后一項與前一項的比為定值. 在等差數(shù)列求和的過程中，由等差數(shù)列的通項公式可以得到[a1+an=2a1+][n-1d=a2+an-1=…]，然而在這個具體的等比數(shù)列問題里，則有[1+263≠2+262≠22+261≠…]，無法構(gòu)造出類似等差數(shù)列中的兩項和相等的形式，所以“倒序相加法”行不通.

教師在學生講述的過程中用板書輔助，見副板書的右側(cè). 副板書如圖1所示.

教師追問：等差數(shù)列能用“倒序相加法”求和是由等差數(shù)列的定義和通項公式的特點這個核心知識決定的. 那么，類比思考，要尋找適合求等比數(shù)列前[n]項和公式的推導方法，我們應該從等比數(shù)列的哪些知識入手呢？

教師追問的意圖是讓學生意識到要抓住等比數(shù)列的定義及通項公式，尋找適合的方法構(gòu)造相同項.

為了進一步啟發(fā)學生思考，教師指出：等差數(shù)列前[n]項求和公式的推導是通過構(gòu)造相同的項，達到減少項數(shù)的目的，進而化簡求和. 我們不妨借鑒這個思路，結(jié)合等比數(shù)列的特點進行求和. 教師在講解過程中輔以板書，見圖1的左側(cè).

【實施意圖】圖1是一幅完整的副板書，呈現(xiàn)的目的是將等差數(shù)列求和公式推導過程中的重要知識點有條理地羅列出來，作為學生類比思考和繼續(xù)探究的支架. 既喚醒學生的先驗知識經(jīng)驗，又啟發(fā)學生遷移“減少項數(shù)”的思想，結(jié)合等比數(shù)列的特點進行公式推導. 簡潔醒目的板書既能幫助學生迅速把握重點，也能夠體現(xiàn)數(shù)學的簡潔之美.

2. 問題解決

教師提問：讓我們再次思考如何化簡[S64=1+2+][22+…+263]. 同學們先獨立思考，然后以四人為一個小組交流探討.

教師巡視、聆聽并參與個別小組的討論，發(fā)現(xiàn)一部分學生嘗試在等式兩邊同時乘以[2]，但沒有考慮到關(guān)聯(lián)原等式;也有部分學生寫成[21=222=…=263262=2]，然而，學生沒有學習過合分比定理，不能想到構(gòu)造[2+22+…+2631+2+…+262]，故不知道后面如何繼續(xù)探究.

在此情況下，教師進一步啟發(fā)：有一些同學寫成[21=222=…=263262=2]的形式，但是不知道如何利用. 能想到這個形式非常好，但是由于我們現(xiàn)有的知識有限，暫時還不能有效利用它，課后老師補充知識后再一起探究. 另外，還有些同學在等式兩邊同時乘以[2]，得到了一個新等式，得到的這個新等式與原等式之間有什么關(guān)系呢？請大家一起看黑板思考.

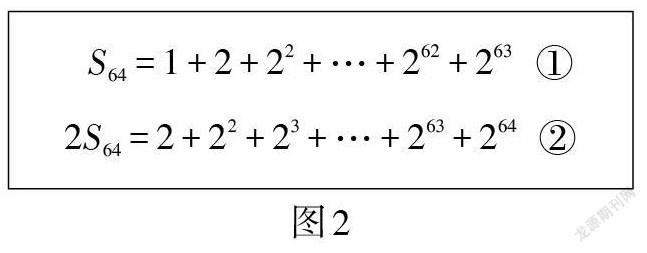
這時，教師板書兩個等式，將學生構(gòu)造出的新和式寫在原和式①的正下方，讓每一項對齊，并標編號②，如圖2所示.

兩個等式規(guī)整對齊能讓學生感受數(shù)學的對稱之美，也便于學生發(fā)現(xiàn)相同項之間的位置關(guān)系，為后續(xù)教學做鋪墊.

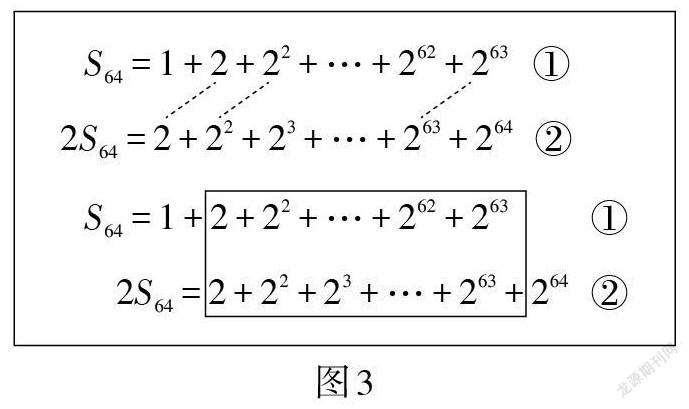
在教師的啟發(fā)下，學生發(fā)現(xiàn)兩個等式中有很多相同項. 這時，教師及時追問：這些相同項的位置有什么特點？學生不難發(fā)現(xiàn)他們的位置是錯開的. 這時，教師用斜線連接上下兩項錯位的相同項，幫助學生直觀感受，并將兩個等式重新寫成相同項對齊的方式，框選相同項部分，如圖3所示.

教師啟發(fā)：怎樣利用兩個等式中的相同項，達到減少項數(shù)的目的呢？

教師一邊啟發(fā)一邊指著副板書的左側(cè)說：減少項數(shù)，構(gòu)造相同的項.

經(jīng)過啟發(fā)，學生聯(lián)系解方程時“消元”的經(jīng)驗，將兩式相減消去相同項，計算得到結(jié)果[S64=264-1].

教師進一步啟發(fā)：因為這些相同項的位置是錯開的，我們給這個方法取個什么樣的名字呢？在問題導引下，學生類比之前“倒序相加法”的起名方法，取名“錯位相減法”，這個名稱就自然誕生了.

接下來，教師在黑板上板書學生的思考過程，如圖4所示.

【實施意圖】在嘗試自主探索的過程中，學生依據(jù)前一環(huán)節(jié)教師的啟發(fā)鋪墊，把思考的重點放在如何利用等式前后兩項的關(guān)系上. 對于這一關(guān)系，學生自然會有不同的利用形式，其探索過程處在邊走邊看的態(tài)勢，故而教師的適時引導很重要. 圖2和圖3是把學生的思維顯性化和直觀化，也給予學生更直接的視覺沖擊.

3. 歸納提升

教師引導：梳理一下剛才的問題解決過程，能利用錯位相減法解決等比數(shù)列求和問題的根本原因是什么？實現(xiàn)減少項數(shù)的過程中，我們利用了等比數(shù)列的什么知識？

在教師的引導下，學生總結(jié)得出：因為等比數(shù)列的前一項乘以公比[2]以后就變?yōu)榱撕笠豁棧覀冞\用的是等比數(shù)列的定義和通項公式的特點. 教師這時在副板書左側(cè)的圖中增加“等比數(shù)列的定義”字樣，再增加箭頭，寫上“錯位相減法”，形成圖5，從而在同一個圖中體現(xiàn)兩類數(shù)列求和過程的共性和區(qū)別.

【實施意圖】圖5是對副板書左側(cè)的完善，呈現(xiàn)等差數(shù)列和等比數(shù)列前[n]項和公式的推導方法的探索路徑，讓學生意識到兩者的基本路徑是一樣的，方法的不同取決于等差數(shù)列和等比數(shù)列定義的本質(zhì)不同，這是一種類結(jié)構(gòu)化路徑的體現(xiàn).

4. 類比遷移

教師提問：類比剛才的求和過程，如何求以[a1]為首項、以[q]為公比的等比數(shù)列的前[n]項和[Sn]呢？

教師在主板書上板書一般等比數(shù)列的求和式，便于學生類比首項為1、公比為2的等比數(shù)列的前64項和[S64=][1+2+…+263]的化簡過程，如圖6所示.

【實施意圖】學生根據(jù)具體等比數(shù)列求和問題的解決經(jīng)驗，完全有能力主動進行知識遷移. 教師在此過程中注意引導學生對公比[q]討論分析. 教師根據(jù)學生的匯報，完善求和公式的推導過程. 至此，公比[q≠1]的等比數(shù)列前[n]項和公式推導完成.

教師啟發(fā)：利用錯位相減法推導得到公比[q≠1]時等比數(shù)列前[n]項和公式[Sn=a11-qn1-q=a1-anq1-q]. 整體分析等差數(shù)列和等比數(shù)列的求和公式的推導過程，你是否把握了數(shù)列求和的關(guān)鍵？

本節(jié)課主板書和副板書最終呈現(xiàn)效果，如圖7所示.

【實施意圖】回顧本節(jié)課的探究經(jīng)歷，學生深切感受到數(shù)列求和應該結(jié)合數(shù)列本身的特征，在此基礎上尋找適當?shù)姆椒p少求和式的項數(shù)，以化簡求和. 整個過程中主板書既引導學生進行數(shù)學思考，又再現(xiàn)學生的思維結(jié)果，將求和公式推導過程完整展示. 從板書布局上看，左右對比，體現(xiàn)由特殊到一般的數(shù)學思想;從公式書寫上看，上下對稱，體現(xiàn)數(shù)學的對稱美與簡潔美.

三、實踐反思

在數(shù)學課堂教學中，教師不應該僅利用板書呈現(xiàn)知識和問題解決的過程，更應該注重利用板書激發(fā)學生進行數(shù)學思考. 上述實例中，教師利用副板書激活學生的先驗知識經(jīng)驗，利用主板書啟發(fā)學生進行數(shù)學思考，引導學生探索錯位相減法的本質(zhì)，推導等比數(shù)列求和公式，主、副板書巧妙聯(lián)系起來，體現(xiàn)知識之間的聯(lián)系與區(qū)別. 總體上看，整個板書是對數(shù)列求和知識點的濃縮，突出知識間的整體性和差異性，幫助學生構(gòu)建完整的知識體系. 這樣的數(shù)學教學不僅有利于提升學生的數(shù)學思維能力，讓學生深刻體會到數(shù)學教學的形象性、審美性，而且自然地利用學生已有的先驗知識，進行類比、遷移和創(chuàng)新，直至內(nèi)化，有效達到了培養(yǎng)和發(fā)展學生數(shù)學學科核心素養(yǎng)的目的.

板書藝術(shù)作為數(shù)學教學藝術(shù)中不可缺少的一個組成元素，在數(shù)學課堂教學中發(fā)揮著重要作用. 它既是教師頭腦中知識結(jié)構(gòu)的再現(xiàn)和課堂設計的縮影，又是學生進行自主知識建構(gòu)的模板和學生認知的“腳手架”. 同時，板書是促進師生互動、提高課堂教學效率的有效輔助手段. 巧妙運用板書，有助于啟發(fā)、引導學生進行數(shù)學思考，幫助學生主動發(fā)現(xiàn)解決問題的方法和策略，從而促進學生數(shù)學學科核心素養(yǎng)的發(fā)展.

在信息技術(shù)迅猛發(fā)展的當下，傳統(tǒng)板書逐漸被多媒體所取代，這一現(xiàn)象需要引起教師的重視. 數(shù)學學習重在培養(yǎng)學生的數(shù)學思維，傳統(tǒng)板書有助于教師引導和呈現(xiàn)學生思維的發(fā)生、發(fā)展過程. 希望此文能給一線教師帶來一些啟迪，并引發(fā)對數(shù)學課堂傳統(tǒng)板書的重視和研究.

參考文獻：

[1]張倩. 中學數(shù)學幾何教學板書設計研究[D]. 上海：上海師范大學，2018.

[2]陳算榮. 數(shù)學核心素養(yǎng)落地課堂：五“E”教學模式解析[J]. 中學數(shù)學教學參考（下旬）2017（11）：62-64.

[3]陳算榮. 核心素養(yǎng)視角下數(shù)學教學實施的理論與實踐：基于“等比數(shù)列的前[n]項和”同課異構(gòu)的比較與評價[J]. 教育研究與評論（中學教育教學），2019（5）：62-67.

[4]田文波，田靜波. 新課程下板書設計的重要性[J]. 課程教育研究，2013（31）：55-56.