基于樣本的優化

張智杰，孫曉明，張家琳，陳衛

1. 中國科學院計算技術研究所，北京 100086；2. 中國科學院大學，北京 100049；3. 微軟亞洲研究院，北京 100080

1 引言

為了解決實際生活中遇到的統籌優化問題，人們通常要建立一個問題模型，并確定模型的參數和優化目標函數，然后設計算法進行求解。然而，在大數據時代，許多應用場景無法提供足夠的信息來確定模型參數和目標函數。人們只能通過觀察到的歷史樣本數據來獲取模型的信息，并進行優化。在這類場景下，人們通常使用機器學習的方法進行處理：首先近似地學習一個替代的目標函數，然后優化這個替代的函數。盡管這個方法在實際應用中獲得了巨大的成功，但是在很多實際問題中，這個方法缺乏理論上的保證。事實上，它可能存在如下兩個問題：① 即使針對原函數的優化問題是可求解或者可近似求解的，但是針對替代函數的優化問題也可能是不可近似的，這是因為替代函數可能丟失了一些原函數所具有的良好性質（如次模性）；② 即使替代函數是可近似的，而且從整體上看和原函數很接近，但是它的最優解相較于原函數的最優解也可能是一個很差的近似。這些擔憂自然地引出了如下問題：人們是否真的能從一系列樣本數據中求解目標函數的優化問題？

1.1 樣本優化模型

為了回答基于樣本的組合優化是否可能的問題，Balkanski E等人[1]定義了另一種計算模型——樣本優化（optimization from samples，OPS）模型。

定義1（OPS模型）給定參數如果存在算法A（不一定是多項式時間的），給定參數并將樣本集作為輸入，其中，Si獨立同分布于D，，算法A返回S∈M，并滿足

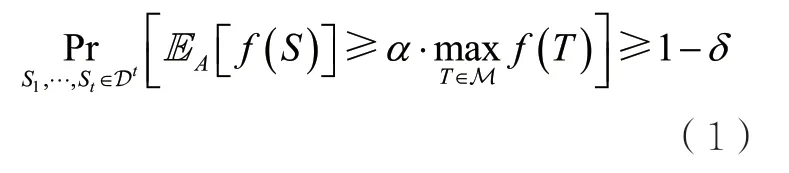
則稱函數類 在分布D下對于約束M是α-可優化的。其中，α被稱為近似比，表示算法的解與最優解的比值。算法使用的樣本數t被稱為算法的采樣復雜度。顯然，樣本分布D會顯著影響函數類F在OPS模型下的可優化性。例如，當D總是返回空集作為樣本時，不可能對問題得到任何有意義的近似比。因此，人們轉而希望在某些“合理的”樣本分布下，優化是可能的。此外，對于在查詢模型下具有常數近似比的問題，人們通常希望它在OPS模型下也具有常數近似比。對于這類問題，如果存在分布D，當將給定多項式數量的獨立同分布于D的樣本作為輸入時，問題存在常數近似算法，則稱它們（在OPS模型下）是可優化的；反之，則稱它們是不可優化的。

樣本優化模型在目標函數可優化且可學習的情況下最具研究價值。Balcan M F等人[2]首先定義了集合函數的PMAC（probably mostly approximately correct learnability）-可學習性。

定義2（PMAC-可學習性）對于函數類F和參數，如果給定參數并將樣本集作為輸入，其中，Si獨立同分布于D，，存在輸出，并滿足

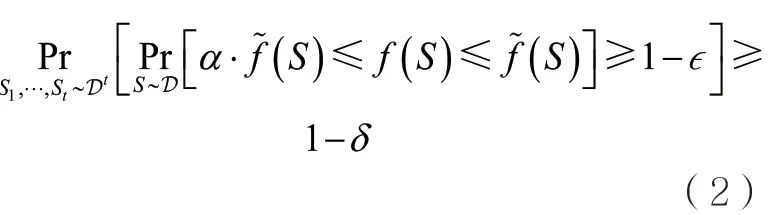
如果在每個分布D上都是α-PMAC-可學習的，則稱F在分布D上是α-PMAC-可學習的。

由定義2可知，函數類F是α-PMAC-可學習的意味著在大多數輸入集合上（相對于分布D而言），存在某種算法學習到的函數值與真實的函數值很接近。并且，人們通常要求這對于任意的分布D均成立。而函數可優化性的定義只要求存在分布D使之成立即可。

最后，覆蓋函數和影響力函數是這一領域的重要研究對象，下面介紹它們的定義。給定二部圖G=(L,R,E)，其中，L和R分別表示左右兩邊的點集，E表示點之間的邊集。覆蓋函數定義為集合S?L的鄰居的個數，即。而最大覆蓋問題要求選取最多k個左邊的節點，并最大化它們覆蓋的鄰居數。換言之，它要求在基數約束下最大化一個覆蓋函數，即

影響力函數是覆蓋函數在一般有向圖上的推廣。它被定義在社交網絡（有向圖）G=(V,E,p)上，其中，V表示點集，E表示邊集，p表示概率向量，每條邊(u,v)∈E具有概率。每個節點存在激活和未激活兩種狀態。給定t=0的初始激活節點S0（被稱為種子集合），其他節點以如下方式被激活：在時刻t=1,2,3,…，首先令接著，對于每個節點，令表示v的入鄰居，每個節點會以概率puv獨立地激活節點v。v一旦被激活，就會被加入St中。節點被激活的過程是不可逆的，因此有。一旦沒有新的節點被激活，此過程終止。顯然，這一過程最多進行n-1步。因此，可以使用來表示激活節點的隨機序列。上述傳播過程被稱為獨立級聯傳播模型。給定S0，定義為最終的激活節點。影響力函數 被定義為，即種子集合S激活的節點數的期望。影響力最大化問題要求選取一個大小不超過k的種子集合，并最大化它激活的期望節點數，即

1.2 不可近似性結果

Balkanski E等人[1]在OPS模型下研究了最大覆蓋問題的近似性，即在基數約束下最大化一個覆蓋函數。此前，覆蓋函數被證明是(1-)-PMAC可學習的[4]。此外，在查詢模型下，最大覆蓋問題是（1-e-1）-近似[5]的。因此，人們相信若采取“先學習后優化”的策略，最大覆蓋問題在OPS模型下是可優化的。然而，令人驚訝的是，Balkanski E等人[1]證明了在OPS模型下，最大覆蓋問題實際上是不存在常數近似的。換言之，盡管覆蓋函數是可學習的，卻不是可優化的。這使基于樣本的組合優化問題得到一個否定性的回答。Balkanski E等人[1]的證明中構造了一類PMAC-可學習的覆蓋函數，這類函數在絕大多數輸入集合上能近似得很好，然而，這些近似良好的集合恰恰不是問題的最優解集，并且最優解與這些集合的函數值有較大差別。這解釋了樣本優化模型下不可近似性結果的由來。從概念上說，基于“先學習后優化”的思路，原問題通常可以被拆解為采樣模型下的學習問題與查詢模型下的優化問題。盡管這兩個問題都是容易解決的，將它們結合起來卻不能解決樣本優化問題。這是因為這兩個問題的子目標沒有完全對應，學習任務的子目標只要求在絕大多數集合上學得好，但這些學得好的集合恰恰是在優化意義上比較差的集合，因此對于原函數的優化沒有幫助。

OPS模型十分容易被推廣到其他優化問題上，而類似的不可近似性結果也出現在其他多個優化問題中。

眾所周知，無約束次模函數①對于，如果有則稱函數是次模的。最小化問題可以在多項式時間內精確求解[6]。此外，當假定函數的取值在[0,1]之間時，可以證明以均等的概率返回空集或者全集，就能夠得到一個1/2的加性近似[7]。針對這一問題，Balkanski E等人[7]定義了如下OPS模型。

定義3給定參數，如果存在算法A，給定參數并將樣本集作為輸入，其中，Si獨立同分布于，算法A返回，并滿足

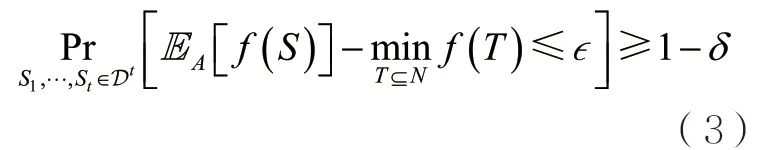
Balkanski E等人[7]證明了，在OPS模型下存在一類PAC-可學習的取值在[0,1]之間的次模函數，對于任意分布D，將給定多項式數量的獨立同分布于D的樣本作為輸入，這類函數不存在的加性近似。

上述不可近似性結果并不局限于組合優化中。眾所周知，凸函數的最小化問題也是多項式時間可解的。針對這一問題，Balkanski E等人[8]定義了如下OPS模型。

定義4給定參數，如果存在算法A，給定參數并將樣本集作為輸入，其中，xi獨立同分布于，算法A返回，并滿足

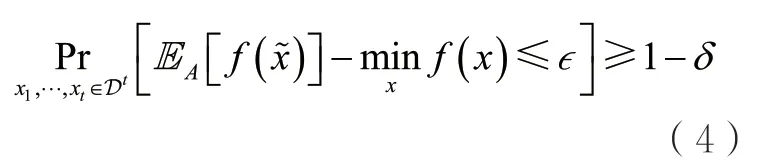
Balkanski E等人[8]證明了，在OPS模型下，存在一類PAC-可學習的凸函數族，對于任意分布D，將給定多項式數量的獨立同分布于D的樣本作為輸入，這類函數不存在(1/2-O(1))的加性近似。這個界是緊的（相當于最優的），這是因為可以證明返回x=(1/2,1/2,…,1/2)就能達到1/2的加性近似。

上述幾個結果表明，許多在查詢模型下可以優化的問題在采樣模型下卻是不可優化的，盡管從樣本中可以學習到這些問題的目標函數。這說明了函數是可學習的并不意味著它是可優化的。

1.3 算法結果

后續有一系列工作嘗試繞開OPS模型下的不可近似性結果[9-13]。這樣的嘗試大致可以分為3類。

第一類方法假設目標函數f擁有額外的性質。例如，Balkanski E等人[10]考慮了f是曲率為的單調②對于，如果， 則稱函數是單調的。次模函數的情況。曲率[14]是衡量單調次模函數線性程度的一個度量。曲率越小，函數越接近線性。例如，線性函數和覆蓋函數都滿足單調性和次模性，但是線性函數的曲率為0，而覆蓋函數的曲率為1。Balkanski E等人[10]證明了，在OPS模型下，當樣本分布為約束上的均勻分布時，問題存在近似，并且這個近似比是最優的。線性函數的曲率為0意味著線性函數即使在OPS模型下也是可以精確求解的。而覆蓋函數的曲率為1，這個結果和OPS模型下最大覆蓋問題的不可近似性并不矛盾。

影響力最大化問題是社交網絡研究中的核心問題之一[3]。獨立級聯傳播模型下的影響力函數是單調次模函數的一個重要實例，而覆蓋函數又是此影響力函數的特例。因此，影響力函數在OPS模型下也是不可優化的。由于影響力函數被定義在社交網絡G=(V,E,p)上，為了繞開OPS模型下的不可近似性結果，Balkanski E等人[9]考慮了帶有社區結構的社交網絡上的影響力函數。更具體地說，他們假設G是通過隨機區塊模型（stochastic block model）生成的，因此G可被高概率地劃分為若干社區C1,C2,… ,C?，且社區內部的邊比較稠密，社區之間的邊比較稀疏。他們證明了，對于這樣生成的社交網絡和約束上的均勻分布，影響力最大化問題存在常數近似算法。

可以發現，上述方法不改變OPS模型本身，但是通常要求目標函數具有良好的性質，因此其適用范圍有所限制。

第二類方法弱化了優化目標。Rosenfeld N等人[13]提出了OPS模型的一個變種版本，稱之為DOPS（distributional optimization from samples）模型。

定義5（DOPS模型）給定參數如果存在算法A，對于任意分布D，給定獨立同分布于D的樣本集，參數并將另一批樣本集作為輸入，其中，Si獨立同分布于D，f∈F，，算法A返回并滿足

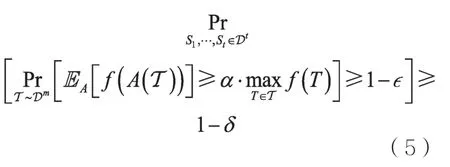
可以發現，在DOPS模型中，不存在約束M，優化目標也不是尋找全局最優解。模型的優化目標是在函數值未知的大小為m的樣本集T中尋找函數值最大的樣本。因此，優化目標取決于樣本分布D。算法可以使用另一批函數值已知的樣本集來收集函數f的信息，并最終達成上述目標。需要注意的是，在OPS模型中，要求樣本數t關于基集合的大小是多項式的，表示問題規模。因此，作為類比，在DOPS模型中，要求t關于m是多項式的。

Rosenfeld N等人[13]證明了一個集合函數類在DOPS模型下是α-可優化的，當且僅當它是α-PMAC-可學習的。這種解決方式恰恰利用了之前“可學習但不可優化”的矛盾之處。函數可學習說明替代函數在絕大多數地方和目標函數很接近，而這里的絕大多數是相對于分布D而言的。如果分布D較偏離函數最優解，則會導致即使替代函數整體上接近目標函數，在最優解附近可能也會偏離較遠，進而使得全局優化目標很難達成。與之相對地，只針對函數值未知的樣本定義的優化目標會更容易達成。但是這個解決方式最終達成的優化目標依賴于樣本數據的分布，并不符合通常對集合函數的優化問題的要求。人們仍然希望相對合理的分布D能為原目標函數的全局最優解提供一定的理論保證。

第三類方法既不假定目標函數滿足額外的性質，也不弱化優化目標，而是假設樣本攜帶額外的結構信息，這樣的樣本被稱為結構化樣本。Chen W等人[11]首先研究了這種方法，針對覆蓋函數提出了OPS模型的一個變種版本——結構化樣本優化（optimization from structured samples，OPSS）模型。

定義6（OPSS模型）給定參數如果存在算法A，給定參數并將樣本集作為輸入，其中，Si獨立同分布于D，為Si在二部圖G上的鄰居，算法A返回S∈M，并滿足

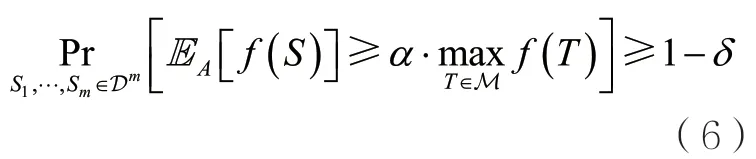
在OPSS模型中，算法不僅知道iS覆蓋的鄰居數，還知道它具體覆蓋了哪些節點，因此掌握了關于函數結構的部分信息。Chen W等人[11]證明了，當分布D滿足可行性、多項式大小的采樣概率和負相關性這3個條件時，最大覆蓋問題在OPSS模型下存在常數近似。因此，通過假設樣本是結構化的，所得結果繞過了OPS模型下的不可近似性結果。

這一結果后來被推廣到獨立級聯模型下的影響力函數最大化問題[12]。在OPSS模型下，算法的輸入是結構化樣本，其中獨立同分布于D，給定的產生遵循獨立級聯模型的傳播過程。Chen W等人[12]證明了當分布是乘積分布時，影響力最大化問題存在常數近似。

可以發現，由于不同目標函數的結構各不相同，因此難以定義通用的OPSS模型，需要基于各個函數的結構特點給出具有針對性的定義。本文將著重介紹OPSS模型下的算法結果。

2 OPSS模型

2.1 最大覆蓋問題

Chen W等人[11]為OPSS模型下的最大覆蓋問題設計了如下算法。

算法1：最大覆蓋問題的OPSS算法

令T1=S1

以等概率返回T1和T2中的一個

算法1以相等的概率返回兩個可行解T1和T2中的一個，其中T1=S1就是第一個樣本，而T2是通過在二部圖上運行標準最大覆蓋問題的k-近似算法得到的。二部圖是原圖G的一個近似，它是由樣本構造出來的。對于節點uL∈ ，定義它在上的鄰居為用來近似它的真實鄰居

直觀的算法設計如下：如果某個單元素集{u}從分布D中被采樣出來，那么算法能完全知曉NG(u)的信息。然而，從D中采樣出來的可能是一個大集S，對于節點uS∈ ，NG(u)的信息被隱 藏 在NG(S)中。幸運的是，如果節點同時屬于兩個樣本S1、S2，那么有。因此，算法1使用包含節點的樣本的鄰居的交集作為節點u的真實鄰居的估計，以便盡可能地揭露u的真實鄰居的信息。

為了對算法1進行嚴格的理論分析，需要假定算法在如下假設下運行。

假設1假設2L上的分布D滿足如下3個條件。

● 可行性。樣本S～D總是可行的，即

● 多項式大小的采樣概率。存在常數c>0，對于每個節點

● 負相關性。對于S～D，隨機變量是負相關的，即

上述3個條件都是非常自然的。特別地，第二個條件意味著L中的所有元素都有足夠的概率被采樣到。第三個條件直觀上意味著u出現在樣本中這一事件的發生會減少其他節點出現在樣本中的概率。顯然，這個條件降低了許多個節點同時出現在樣本中的概率，有助于算法1揭示特定節點的鄰居的信息。一些典型的分布均滿足假設1，例如上的均勻分布 D≤k以及上的均勻分布Dk。基于假設1，可以證明：

定理1對于任意δ∈ ( 0,1)，給定任意標準最大覆蓋問題的k-近似算法，令表示算法1返回的解，OPT表示原圖G上的最優解。如果分布D滿足假設1且樣本數其中，c是假設1中的參數，那么

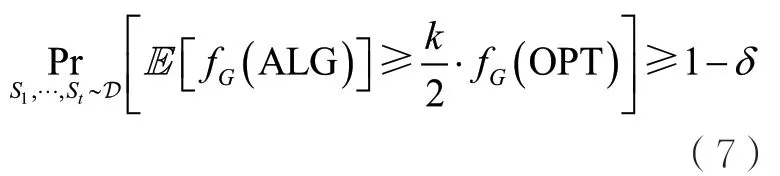
如果只要求常數近似比，則假設1中“可行性”的條件可以被放寬為Chen W等人[11]還證明了如下結論。

● 當樣本分布D為均勻分布 D≤k或 Dk時，存在算法能夠達到近似比。

● 移除假設1中的任意一個條件，存在滿足剩下兩個條件的某個分布D，在這一分布下不存在常數近似算法。這意味著為了得到OPSS模型下最大覆蓋問題的常數近似算法，假設1的3個條件都是必須滿足的。

2.2 影響力最大化問題

Chen W等人[12]采取如下框架求解OPSS模型下的影響力最大化問題：首先學習邊的概率，然后在學習到的社交網絡上求解影響力最大化問題。其中，學習邊概率的任務被稱為網絡推斷（network inference）問題，它的嚴格定義如下：給定結構化樣本，其中獨立同分布于D，給定的產生遵循獨立級聯模型的傳播過程，，要求計算一個概率向量，使得

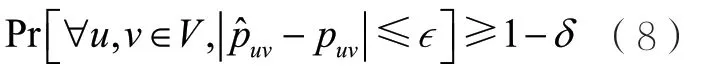
為了求解上述問題，Chen W等人[12]假設產生種子的分布是乘積分布，即對于樣本S～D，事件之間是相互獨立的。

在是乘積分布的假設下，Chen W等人[12]提出了一個高效求解網絡推斷問題的方案。為了描述這一方案，需要定義一些符號。記是激活節點的隨機序列。對于節點u，定義，表示u被選為種子的概率。對于節點v∈V，定義，表示v在一個時間步之內被激活的概率。節點v既有可能因為被選為種子而激活，也有可能被種子激活。因此，ap(v)定義中的隨機性既來自種子分布D，也來自圖G上第一個時間步之內的傳播過程。此 外，定 義表示節點u不是種子時相應的條件概率。Chen W等人[12]的關鍵性觀察如下。

引理1給定任意u,v∈V且u≠v，

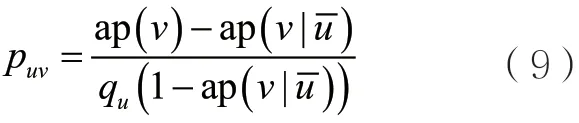
引理1的證明思路如下：在一個時間步之內，節點v或者被節點u之外的節點激活，或者被節點u激活。由于D是乘積分布，可以得到

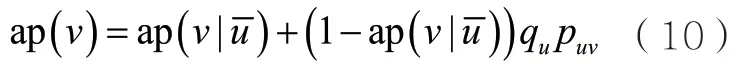
重新排列式（10）便可以得到引理1中的結果。

有了引理1后，就可以通過估計qu、ap(v)和來估計puv。

算法2：網絡推斷算法

對于所有u,v∈V，分別估計和

假設2存在參數和使得

● 對于所有v∈V， ap(v)≤1?α；

在假設2下，可以證明如下定理。

定理2在假設2下，令表示算法2返回的邊的概率，表示真實的邊概率。給定，如果樣本的數量，那么

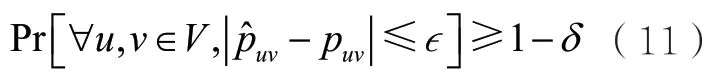
接著介紹如何利用網絡推斷算法解決OPSS模型下的影響力最大化問題。Narasimhan H等人[15]證明了如下引理。

引理2給定S?V和任意兩個概率向量，并滿足，用σp表示定義在圖G= (V,E,p)上的影響力函數，那么

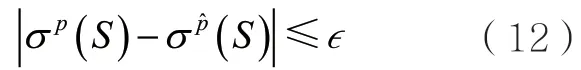
為了得到一個在任何社交網絡上均能運行的OPSS算法，Chen W等人[12]采取了處理最大覆蓋問題時所用的技術。具體地說，算法首先對每個節點v∈V估計ap(v)的值，并比較它們與給定閾值的大小。如果ap(v)大于給定閾值，那就意味著節點v以高概率在一步之內被激活，此時，算法將它的所有入邊的概率設置為1；如果ap(v)小于此閾值，那么假設2的條件被滿足，可以使用網絡推斷算法估計v的所有入邊的概率。經過上述步驟可以得到一張新圖。算法在這張新圖上運行k-近似的影響力最大化算法，并得到一個解。算法使用第一個樣本作為另一個解，最終以等概率返回兩個解中的一個。

算法3：影響力最大化問題的OPSS算法

f or 每個v∈Vdo

else

對于所有u,v∈V，分 別 估 計、和

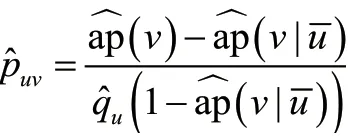
end if

end for

以等概率返回1T和2T中的一個

上述算法與最大覆蓋問題的OPSS算法（算法1）的設計思路是一致的。ap(v)接近1意味著節點v以高概率在一步之內被激活，因此網絡推斷算法的假設不被滿足，算法無法學習到節點v的入邊概率。幸運的是，這同時意味著任意一個樣本都能夠以高概率激活節點v。因此算法無須學習節點v的入邊概率，而是直接把它們設置為1。這樣的設置幾乎不改變樣本激活節點v的概率。

上述設計使得算法能夠處理任意ap(v)，從而移除了假設2中關于ap(v)的條件。而作為代價，算法需要假設樣本的期望大小不超過k/2，從而保證采樣出來的樣本高概率是可行的。因此，算法需要在下面的假設下運行。

假設3存在參數，使得

顯然，假設3的兩個條件都是針對樣本分布的，不針對社交網絡。因此，算法3在任何社交網絡都可以成功運行。可以證明，算法3是一個常數近似算法。

定理3對于任意，給定任意標準影響力最大化問題的k-近似算法，令表示算法3返回的解表示原圖G上的最優解。如果分布D滿足假設3且樣本數那么

最后，若把假設3中的第一個條件改為“存在常數c>0，使得”，仍然能夠通過修改算法得到一個常數近似比。如果，那么可以修改算法得到一個-近似。

3 未來研究方向

樣本優化仍然有許多可以進一步研究的方向。

● 針對OPSS模型下的最大覆蓋問題和影響力最大化問題，降低現有算法的查詢復雜度。此外，目前影響力最大化的OPSS算法假設樣本分布是乘積分布。如何突破這樣的獨立采樣假設是一個十分重要的開放問題，一種可能的方法是將文中的方法與極大似然估計方法結合。

● 對更多的目標函數定義適當的結構化樣本，并研究它們在OPSS模型下的近似性。一個直接的例子是線性閾值模型下的影響力最大化函數（筆者已經得到了這方面的初步結果）。可以發現，OPSS模型是一個表達能力豐富、能夠挖掘函數內在結構性質的模型。因此，在OPSS模型下研究各類優化問題是一個十分有潛力的研究方向。

● 研究更多的方法以繞開標準OPS模型下的不可近似性結果。更多這樣的研究一方面有助于人們應對不同的應用場景，另一方面有助于人們理解樣本數據與函數可優化性的內在聯系。

● 研究從樣本中優化凸函數的可能性。目前所有繞開OPS模型不可近似性結果的方法都是針對集合函數而言的。對于實函數，尤其是具有良好優化性質的凸函數，尚沒有這方面的研究。考慮到凸函數在連續優化中的重要地位，對它的進一步研究是十分必要的。

4 結束語

本文總結了OPS模型及其變種模型下的不可近似性結果和算法成果，并展望了相關的未來研究方向。OPS模型是數據驅動的優化的重要研究方法之一，值得進行更加深入的研究。