對等結構下的相對導航源選擇研究

張天舒 李寅龍

摘 要：在集中式與分布式結構基礎上建立基于對等式結構的模型， 針對對等式結構下無源定位相對導航的源最優選擇問題， 利用高斯-牛頓法設置相對導航卡爾曼濾波器初值使其快速收斂， 定義時間、 位置、 幾何、 綜合誤差因子， 設置不同仿真環境研究距離、 速度、 時間偏差和幾何分布位置對相對導航精度的影響。 仿真表明， 偏差與相對導航精度呈反比關系。 當待定位節點與導航源連線夾角為90°時， 導航精度最高， 導航源直線配置時， 寬基線方案的精度要明顯優于窄基線方案， 且四源定位的精度優于兩源、 三源定位。 本文建立的算法模型能夠較好分析不同因素對定位誤差的影響。

關鍵詞：對等式結構; 相對導航; 卡爾曼濾波; 初始偏差; 幾何分布位置; 雷達信號; 目標跟蹤

中圖分類號：??? TJ765; V294.3 ??文獻標識碼：??? A 文章編號：1673-5048（2021）04-0043-06

0 引? 言

多傳感器目標跟蹤中常采用集中式與分布式結構。 集中式結構中各節點發送數據至融合中心進行信息融合， 對通信和計算能力提出了較高要求[1]。 分布式結構中各節點獨立處理局部觀測數據后匯總到融合中心進行處理， 減輕了通信量、 計算量的負擔， 且能達到與集中式相近的精度[2]。 集中式與分布式結構都依靠融合中心完成全局態勢的信息融合， 但多傳感器以及情報源的信息傳輸可能造成信息爆炸。 在惡劣信息戰環境中， 如果融合中心性能癱瘓， 將對作戰能力造成毀滅性打擊， 因此提出對等式結構以彌補集中式、 分布式結構抗毀性差的缺點。 對等式結構具有無源定位和高精度相對導航的能力， 能夠實時截獲和鎖定節點相對坐標， 間接校正運動節點導航系統的數據， 并傳遞分享自身導航源數據。 P2P技術、 Ad-Hoc網絡、 區塊鏈、 聯合戰術指揮系統數據鏈（JTIDS）等， 都是對等式結構的成熟應用[3]。

針對多傳感器目標跟蹤中相對導航問題， 文獻[4]提出RBF輔助的導航算法修正相對導航的精度。 文獻[5]利用INS/Link-16的高穩定性與高精度性， 通過測距校正相對導航誤差。 在此基礎上， 文獻[6]利用視覺/INS的參數作為狀態變量， 設計EKF濾波器估計相對導航參數。 文獻[7]提出覆蓋濾波算法， 建立了GPS/INS組合導航的無人機隱蔽干擾算法。 文獻[8]建立混合概率模型降低積分誤差， 利用視覺與INS的IMU數據進行自主相對導航。 文獻[9]利用非線性開普勒模型對衛星的觀測能力進行評估分析， 提出了分布式衛星相對導航算法。 文獻[10]基于偽距和超寬帶的特征， 設計相對導航狀態方程對相對狀態進行估計。 文獻[11]提出LM-IEKF算法解決無人機與非合作目標相對導航的問題。

上述算法從慣性導航、 衛星導航、 無人機輔助導航等方面提出相對導航算法， 但有以下缺點： （1）慣性導航的誤差易累積， 需要不斷進行修正; （2）衛星導航在惡劣電磁環境下無法建立良好通信; （3）編隊運動模型較為單一; （4）皆為給定導航源， 并未考慮在導航源較多情況下該如何選擇最優源; （5）考慮了距離、 時間對導航的影響， 但未考慮幾何位置的影響， 沒有對相對導航源選擇的問題進行最優考慮。 本文算法建立在對等式結構下， 增強了節點間的相互聯系， 打破分布式結構中各節點相互孤立的局面， 感知覆蓋范圍廣、 靈活性強、 具有實時性， 建立可快速收斂的相對導航濾波器， 并且從時間、 距離、 幾何分布等方面分析如何進行最優導航源選擇。 在態勢瞬變的現代電子戰中， 若遭遇電磁靜默、 GPS失靈等情況時， 不僅可以更正節點實時位置情報，? 更健

全了輔助監視態勢的編制， 使對等式信息池中對跟蹤/關聯目標的信息交換更可靠， 提高作戰能力上限， 更適應復雜電磁環境并且提高對全局態勢感知的掌握。

1 模型建立

對等式結構實質上是一種分布式、 去中心化的通信模式。 各節點具有同等的地位， 可以互相通信、 共享資源、 協同工作。 節點間交換信息聯結成巨大的信息池， 各節點可有選擇地從中獲取所需信息。 對等式結構中待定位節點可利用TOA（信號到達時間）解算自身與其他源的距離， 并根據導航源發送的位置信息通過多邊測距完成相對導航定位[12]。

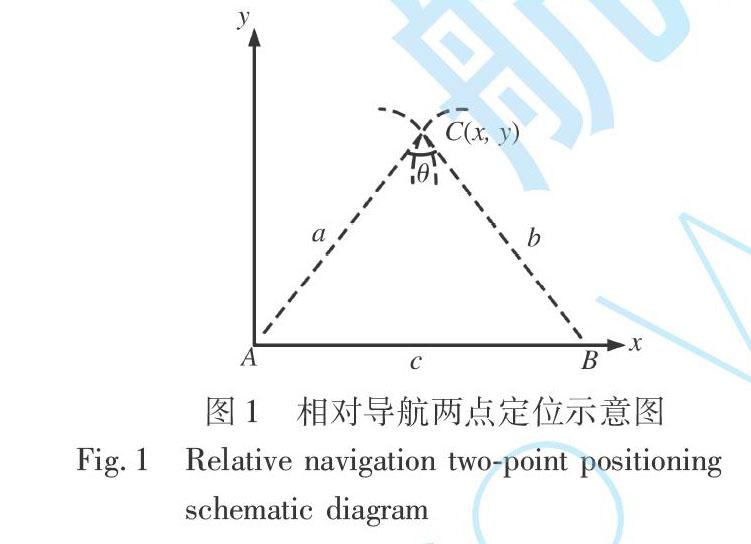
由于系統的導航半徑遠大于工作高度， 忽略高度影響， 將相對導航建立在二維坐標系下， 如圖1所示。 以兩點定位相對導航為例， 節點A， B為相對坐標系中固定節點， 相距為c， 節點C通過TOA測算距離a， b， 又在固定時隙接收到節點A， B的位置坐標完成相對坐標系中的定位。

2 算法步驟

2.1 卡爾曼濾波

假設相對導航選擇i點定位算法， 建立誤差公式：

φi（x， y）=（xi-x）2+（yi-y）2-Ri （1）

式中： （xi， yi）為其他源的坐標; （x， y）為待定位節點坐標; Ri為待定位節點對各源的TOA測距。

利用高斯-牛頓法計算minφi， 以保證卡爾曼濾波持續收斂， 解算偏導如下[13]：

A=x1-xd1…xi-xdiy1-yd1…yi-ydi （2）

φ=φ1（x， y）φi（x， y） （3）

設待定位節點坐標某一初值X0=（x0， y0）， 則有

X1=X0-A（X0）AT（X0）-1A（X0）φ（X0） （4）

不斷迭代直至|XK+1-XK|<δ， δ為設定的閾值， 此時確定的初值使卡爾曼濾波快速收斂， 能夠迅速達到理想精度。

建立卡爾曼濾波的觀測方程如下：

R0=Rc-tac+ε

Rc=（Xt-X）2+（Yt-Y）2 （5）

式中： R0為節點C利用TOA計算的距離值; c為光速; Rc為利用相對坐標計算的距離值; Xt， Yt為其他源發送的位置坐標; X， Y為節點C位置坐標; ta為節點C相對系統時的偏差; ε為量測噪聲。

建立觀測矩陣為

C=-c0X-XtRcY-YtRc00 （6）

設狀態向量為

S=tfXYvxvy （7）

式中： t為相對時間偏差; f為相對時間偏差率; X， Y為節點在相對坐標系中x，? y方向的坐標; vx， vy為節點速度在x，? y方向的分量。

建立狀態轉移矩陣為

A=1t

1

1t

1t

1

1

（8）

建立噪聲擾動矩陣為

Γ=1

1

t

t

t

1 （9）

2.2 定位誤差計算

如圖1所示， 假設節點A處于相對坐標系原點， 節點B處于坐標（cB， 0）處， 節點C選擇節點A， B作為相對導航源， 此時處于相對坐標系的（x， y）處， 通過TOA計算得

a=（t2-t1）cB+ε1 （10）

b=（t4-t3）cB+ε2 （11）

式中： a， b為節點C與節點A， B的距離; t2， t4為節點C向節點A， B發送信號的時間; t1， t3為信號到達時間; ε1， ε2為隨機誤差。

通過平面幾何知識求得

x=a2 + c2B-b22cB （12）

y=2a2b2 + 2a2c2B + 2b2c2B-a4-b4-c4B2cB? （13）

由于x， y與a， b不是線性關系， 將非線性函數用泰勒級數展開， 取零次項和一次項化為線性函數y=fx+f0的形式， 此時有[14]

Dy=E[（fx-fμx）（fx-fμx）′]=

E[f（x-μx）（x-μx）′f′]=

fE[（x-μx）（x-μx）′]f′=fDxf′（14）

假設a， b的誤差服從高斯分布且相互獨立， 則x， y的誤差模型為

Dx=xa2δ2a+ xb2δ2b=a2c2Bδ2a+ b2c2Bδ2b（15）

Dy=ya2δ2a+yb2δ2b=a2b4+a2c4B+a6+2a2b2c2B-2a4b2-2a4c2Bc2B（2a2b2+2b2c2B+2a2c2B-a4-b4-c4B）δ2a+a4b2+b2c4B+b6+2a2b2c2B-2a2b4-2b4c2Bc2B（2a2b2+2b2c2B+2a2c2B-a4-b4-c4B）δ2b（16）

則C點坐標位置方差為

DC=Dx+Dy （17）

源幾何分布位置影響著相對導航的精度， 假設節點C位于節點A， B中軸線的垂線上， 分析此時夾角θ對源位置質量的影響。 此時a=b， 設a=b=kcB， 為簡化計算， 假設此時δ2a=δ2b=δ2， 則式（17）化簡為

DC=8k44k2-1δ2 （18）

將k=12csc（θ2）代入式（18）， 化簡為

DC=2csc2θ×δ2 （19）

2.3 誤差因子

2.3.1 時間及位置誤差因子

定義時間誤差因子為

Qt=bi（k， k-1）+Pi（k， k-1） （20）

式中： bi（k， k-1）為第i個導航源在k時刻對時間偏差的估計值; Pi（k， k-1）為卡爾曼濾波噪聲協方差矩陣在k時刻主對角線上第i個元素。

定義位置誤差因子為

Qp=πxa2δ2a+xb2δ2bya2δ2a+

yb2δ2b=πDxDy（21）

實質上， 位置誤差因子是以Dx， Dy為長短軸的定位誤差等概率橢圓的面積作為衡量位置質量的標準。

2.3.2 幾何誤差因子

幾何誤差要綜合考慮導航源的位置分布， 假設待定位節點真實坐標為（xw， yw）， 待定位節點濾波坐標為（x^w，? y^w）， 導航源坐標為（xi， yi）， i=1， 2， …， n， 定位誤差為（Δxw， Δyw）， 則有

xw=x^w+Δxw

yw=y^w+Δyw（22）

待定位節點與導航源的真實距離為

ρi=（xw-xi）2+（yw-yi）2（23）

待定位節點與導航源的濾波距離為

i=（x^w-xi）2+（y^w-yi）2（24）

根據式（22）～（24）， 將（x^w，? y^w）利用泰勒級數展開， 只保留一階偏導數， 可得

Δ ρ=i-ρi=xi-x^wRΔxw+yi-y^wRΔyw（25）

R=（x^w-xi）2+（y^w-yi）2（26）

將式（25）化簡得

Δ ρ=HΔ x（27）

式中：

Δ ρ=Δ ρ1Δ ρn，? H=x1-x^wRy1-y^wR

xn-x^wRyn-y^wR， Δ x=Δ xwΔ yw。

利用最小二乘法解算定位誤差可得

Δ x=（HTH）-1HTΔ ρ（28）

設G=（HTH）-1， 則定義幾何誤差因子為

Qg=G11+G22（29）

定義綜合誤差因子為

Q=W1（Qt+Qp）+W2Qg（30）

綜合誤差因子是上述三種誤差因子的加權因子， 其中W1， W2為加權系數。

時間、 位置質量因子只需單獨判斷各個源即可， 但考慮幾何質量因子時， 需考慮各個源與待定位節點的位置分布情況。

3 仿真結果

3.1 仿真環境

在對等式結構中存在A， B， C三個節點， 節點C選擇節點A， B作為相對導航定位源。 節點C運動速度隨機在300 ～700 m/s之間， 在0～2π之間隨機選取某一角度做勻速直線運動。

仿真環境1： 節點B的位置坐標在x， y方向分別包含從0 m遞增到300 m的誤差。

仿真環境2： 節點C在x， y方向速度誤差分別從0 m/s遞增到100 m/s， 由慣性導航誤差累積引起的速度漂移服從標準差為0.01 m/s的高斯分布。

仿真環境3： 節點A的時間偏差從10 ns、 100 ns、 300 ns增長到500 ns， 時鐘的時間游走噪聲服從標準差為10-10 s的高斯分布。

仿真環境4： 節點A， B， C的距離偏差服從均值為10 m、 標準差為100 m的高斯分布， 速度偏差服從均值為10 m/s、 標準差為10 m/s的高斯分布。

仿真環境5： 假設存在編隊節點A～G， 以節點A為原點建立相對坐標系， 各節點飛行位置參數如表1所示， 各節點飛行編隊模型如圖2所示。

3.2 仿真分析

3.2.1 距離偏差對相對導航的影響

如圖3所示， 在仿真環境1的條件下， 節點B的位置坐標中含有x， y方向的距離偏差， 距離偏差以50 m為步長， 從0 m遞增到300 m， 此時， 節點C濾波解算出相對導航系中與節點B的相對距離值應是定值， 但距離值隨著初始距離偏差的增加而增加， 說明導航誤差不斷增大， 并且兩者呈近似線性關系。

3.2.2 速度偏差對相對導航的影響

如圖4所示，? 在仿真環境2的條件下，? 節點C由于慣性導航累積誤差在x， y方向上產生從0 m/s遞增到100 m/s的速度誤差， 速度誤差影響卡爾曼濾波精度。 此時， 卡爾曼濾波解算的相對導航距離隨著速度誤差的增加而增加， 且相比距離偏差， 誤差增長的趨勢越來越快。

3.2.3 時間偏差對相對導航的影響

如表2所示， 在仿真環境3的條件下， 節點A的時間偏差從10 ns， 100 ns， 300 ns增長到500 ns， 數據產生時間異步， 對解算出x， y方向的距離造成誤差。 在時間偏差不超過100 ns時， 仍得到高精度位置解。 在時間偏差不超過300 ns時， 仍得到收斂的位置解， 隨著時間偏差的增大， 距離誤差不斷增大， 兩者呈正比關系。

3.2.4 幾何分布位置對相對導航的影響

在仿真環境4的條件下， 假設節點C位于圖5所示相對坐標系的（0， 100 km）處開始做水平往返運動， 節點A， B從原點出發， 同速度向相反方向運動至100 km處， 圖6所示為節點A， B在x軸移動距離與節點C位置方差的三維圖像。 仿真表明， 當節點A， B與原點距離低于30 km時， 節點C位置方差極大， 超出30 km后節點C位置方差逐漸下降。 在節點A， B距原點位置均為100 km時， 位置方差達到最低值， 此時節點C與節點A， B連線的夾角為90°， 符合式（19）的理論預期。

假設節點A， B固定于相對坐標系的（-100 km， 0）和（100 km， 0）處， 節點C從（0， 10 km）處出發沿y軸逐漸向上移動， 仿真節點C的x， y方向誤差與移動距離的關系如圖7所示， 隨著移動距離的不斷增長， 節點C的y方向誤差逐漸增加， x方向誤差逐漸減小。 在移動距離為100 km時， x， y方向誤差相等， 此時節點C與節點A， B的連線夾角為90°。 若節點C并不處于節點A， B連線的中垂線上， 當連線夾角小于90°時， 徑向誤差是節點C位置誤差的主要來源， 反之， 切向誤差為位置誤差的主要來源。

仿真環境5條件下， 以節點B， D， E， G作為導航源， 假設節點A， C， F所在直線為相對導航坐標系的y軸， 仿真得到幾何誤差因子如圖8所示。 隨著y軸坐標的逐漸增加， 幾何誤差因子先減小后增加， 在坐標約-2 800 m處預計取得最小值。 當y軸坐標超過2 000 m時， 誤差因子上漲較快， 在實際編隊中可限制待定位節點位置以提升導航精度。

仿真環境5條件下， 仿真不同導航源數量對幾何誤差因子的影響如圖9所示。 導航源（2）表示導航源為節點B， D; 導航源（3）表示導航源為節點A， E， G; 導航源（4）表示導航源為節點B， D， E， G。 隨著待定位節點在y軸位置的逐漸增加， 幾何誤差因子先減小后增加， 且各情況中取得最低幾何誤差因子的y軸位置并不相同。 仿真結果表明， 四源定位的精度優于兩源、 三源定位。

不同導航源配置方案如表3所示， 各方案下幾何誤差因子如表4所示。 在三導航源按照直線配置時， 寬基線配置的導航精度相比窄基線配置有明顯提升。 在三導航源按照三角形配置時， 導航精度明顯優于直線配置， 其中等邊三角形配置的導航精度相比等腰三角形配置稍高， 兩者相差很小。 導航源數量為4時， 精度優于三導航源配置， 且Y型配置相比菱形配置的導航精度高。

4 結 束 語

針對對等結構下相對導航最優源選擇問題， 本文設計了相對導航6狀態卡爾曼濾波器， 并且利用高斯-牛頓法設定濾波器初值使其快速收斂。 對影響相對導航定位精度的距離、 速度、 時間偏差以及幾何分布位置等因素進行仿真， 設置了5種仿真環境。 仿真表明， 隨著距離、 速度、 時間偏差的增加， 距離誤差不斷增大， 相對導航精度逐漸降低。 分析幾何分布位置對導航的影響， 仿真表明， 當待定位節點與導航源連線夾角為90°時， 方差最小; 當夾角小于90°時， 徑向誤差是定位誤差的主要來源; 當夾角大于90°時， 切向誤差是定位誤差的主要來源。 導航源直線配置時， 寬基線方案的精度要明顯優于窄基線方案， 且四源定位的精度優于兩源、 三源定位。

參考文獻：

[1] Subedi S，? Zhang Y D，? Amin M G，? et al. Cramer-Rao Type Bounds for Sparsity-Aware Multi-Sensor Multi-Target Tracking[J]. Signal Processing，? 2018，? 145：? 68-77.

[2] Ge Q B，? Wei Z L，? Cheng T F，? et al. Flexible Fusion Structure-Based Performance Optimization Learning for Multisensor Target Tracking[J]. Sensors，? 2017，? 17（5）： 1045-1050.

[3] Khamayseh Y，? Yassein M B，? Abu-Jazoh M. Intelligent Black Hole Detection in Mobile AdHoc Networks[J]. International Journal of Electrical and Computer Engineering （IJECE），? 2019，? 9（3）：? 1968-1977.

[4] 孫瑤潔，? 熊智，? 李文龍，? 等. 基于RBF神經網絡的相對導航信息融合方法[J]. 航空計算技術，? 2019，? 49（6）：? 27-32.

Sun Yaojie，? Xiong Zhi，? Li Wenlong，? et al. Relative Navigation Information Fusion Method Based on RBF Neural Network[J]. Aeronautical Computing Technique，? 2019，? 49（6）：? 27-32. （in Chinese）

[5] 郝菁，? 蔚保國，? 何成龍. 基于慣導/數據鏈的動態相對定位方法[J]. 計算機測量與控制，? 2018，? 26（10）：? 191-195.

Hao Jing，? Yu Baoguo，? He Chenglong. Dynamic Relative Positioning Method Based on Inertial Navigation and Data Link[J]. Computer Measurement & Control，? 2018，? 26（10）：? 191-195. （in Chinese）

[6] 張世杰，? 寧明峰，? 陳健. 非合作目標視覺/慣導相對導航及敏感器自標定方法[J]. 國防科技大學學報，? 2019， 41（6）： 25-32.

Zhang Shijie，? Ning Mingfeng，? Chen Jian. Method of Vision/Inertial Relative Navigation for Non-Cooperative Target and Sensors Self-Calibration[J]. Journal of National University of Defense Technology，? 2019， 41 （6）：? 25-32. （in Chinese）

[7] Guo Y，? Wu M P，? Tang K H，? et al. Covert Spoofing Algorithm of UAV Based on GPS/INS-Integrated Navigation[J]. IEEE Transactions on Vehicular Technology，? 2019，? 68（7）：? 6557-6564.

[8] Liu W L，? Wu S T，? Wen Y M，? et al. Integrated Autonomous Relative Navigation Method Based on Vision and IMU Data Fusion[J]. IEEE Access，? 2020，? 8（99）： 51114-51128.

[9] Su Q Y，? Huang Y. Observability Analysis and Navigation Algorithm for Distributed Satellites System Using Relative Range Measurements[J]. Journal of Systems Science and Complexity，? 2018，? 31（5）：? 1206-1226.

[10] 熊駿，? 熊智，? 于永軍，? 等. 超寬帶測距輔助的無人機近距離相對導航方法[J]. 中國慣性技術學報，? 2018，? 26（3）：? 346-351.

Xiong Jun，? Xiong Zhi，? Yu Yongjun，? et al. Close Relative Navigation Algorithm for Unmanned Aerial Vehicle Aided by UWB Relative Measurement[J]. Journal of Chinese Inertial Technology，? 2018，? 26（3）：? 346-351.（in Chinese）

[11] 朱云峰，? 孫永榮，? 趙偉，? 等. 包含乘性噪聲自適應修正的非合作目標相對導航算法[J]. 航空學報，? 2019，? 40（7）：? 240-250.

Zhu Yunfeng，? Sun Yongrong，? Zhao Wei，? et al. Relative Navigation Algorithm for Non-Cooperative Target with Adaptive Modification of Multiplicative Noise[J]. Acta Aeronautica et Astronautica Sinica，? 2019，? 40（7）：? 240-250.（in Chinese）

[12] 劉駿，? 田福慶，? 孫世巖. JTIDS中時差導航定位方法與性能分析[J]. 彈箭與制導學報，? 2006，? 26（2）：? 659-661.

Liu Jun，? Tian Fuqing，? Sun Shiyan. The Navigation by Time-Difference-of-Arrival and Performance Analysis in JTIDS[J]. Journal of Projectiles，? Rockets，? Missiles and Guidance，? 2006，? 26（2）：? 659-661.（in Chinese）

[13] 武楠，? 王華，? 匡鏡明. JTIDS相對導航性能分析和仿真[J]. 系統工程與電子技術，? 2005，? 27（3）：? 464-466.

Wu Nan，? Wang Hua，? Kuang Jingming. Performance Analysis and Simulation of JTIDS Relative Navigation[J]. Systems Engineering and Electronics，? 2005，? 27（3）：? 464-466.（in Chinese）

[14] 曹可勁，? 朱銀兵，? 崔國恒. 基于幾何位置的JTIDS定位誤差建模與分析[J]. 海軍工程大學學報，? 2010，? 22（3）：? 97-101.

Cao Kejin，? Zhu Yinbing，? Cui Guoheng. Error Modeling and Analy-sis of JTIDS Based on Geometrical Position[J]. Journal of Naval University of Engineering，? 2010，? 22（3）：? 97-101.（in Chinese）

Research on Relative Navigation Source Selection in

Peer-to-Peer Structure

Zhang Tianshu ， Li Yinlong

（Naval Aviation University，? Yantai 264001， China）

Abstract：? On the basis of centralized structure and distributed structure，? the model based on peer-to-peer structure is established. Aimed in the problem of source optimal selection for passive location relative navigation under peer-to-peer structure，? the Gauss-Newton method is used to set the initial value of relative navigation Kalman filter to make it converge quickly. With defining time，? position，? geometry and synthetic error factors，? and setting different simulation environments，? the influence of distance，? speed，? time deviation and geometric distribution position on relative navigation accuracy is studied. The simulation results show that the deviation is inversely proportional to the relative navigation accuracy，? and the navigation accuracy is the highest when the connecting angle between the? node to be located and the navigation source is 90°，? the accuracy of the wide baseline scheme is significantly better than that of the narrow baseline scheme when the navigation source? is configured linearly，? and the accuracy of four-source positioning is better than that of two-source or three-source positioning. The algorithm model established in this paper is able to analyze the influence of different factors on positioning errors.

Key words：? peer-to-peer structure; relative navigation; Kalman filter; initial deviation; geometric distribution position; radar signal; target tracking