海洋運動對臺風過境全過程水平風速特性的影響

員亦雯，柯世堂，2，*，王 碩，2，趙永發(fā)，杜 琳，張 偉

(1.南京航空航天大學 土木與機場工程系，南京 210016；2.南京航空航天大學 江蘇省風力機設(shè)計高技術(shù)研究重點實驗室，南京 210016)

0 引 言

我國位于太平洋西岸并擁有綿長海岸線，是世界上遭受臺風災(zāi)害最為嚴重的國家之一。準確掌握臺風風參數(shù)對工程結(jié)構(gòu)抗風安全具有重要指導(dǎo)意義。臺風[1]是由復(fù)雜渦系組成的近似于圓形的大氣渦旋系統(tǒng)，現(xiàn)行主要臺風模型源于20世紀70年代Batts提出的第一代臺風風場模型[2]和Meng提出的改進工程模型[3]，可在滿足基本精度的前提下實現(xiàn)大量臺風樣本的快速隨機模擬。隨后我國學者針對臺風模擬參數(shù)的敏感性和臺風模型在我國沿海地區(qū)極值風速預(yù)測的應(yīng)用開展了許多研究[4-8]，但臺風模擬理論方法仍采用多個物理場不耦合的假定，預(yù)測結(jié)果過度依賴實測數(shù)據(jù)校準和關(guān)鍵參數(shù)取值經(jīng)驗，缺乏波浪、海流等海洋運動對臺風過境全過程水平風速影響研究，一定程度限制了單個工程臺風模型應(yīng)用于土木工程結(jié)構(gòu)設(shè)計風速的預(yù)測精度。

目前針對海洋運動與臺風之間耦合作用的研究，主要集中于對風、浪、流模擬方法及海洋運動與臺風之間相互影響的探討[9-18]。關(guān)皓等[15]基于大氣模型MM5-海洋模型、POM-海浪模型WW3的三元耦合模式系統(tǒng)，模擬研究了兩種南海典型臺風過程，結(jié)果表明波浪效應(yīng)阻礙了臺風系統(tǒng)的發(fā)展，增強了海表應(yīng)力，加大了海面降溫幅度和海流近慣性振蕩的振幅。徐海波等[16]基于大氣模型WRF-海洋模型ROMS-海浪模型SWAN耦合模擬了臺風“Megi”過程中海洋與大氣變化過程，研究表明海浪作用使得臺風后部風速減小約3～5 m/s，加劇的海洋混合也導(dǎo)致了更大程度的降溫。Liu等[17]基于耦合模式平臺WRF-SWANPOM對理想熱帶氣旋進行數(shù)值模擬研究，結(jié)果表明海氣耦合對熱帶氣旋強度的總體影響是由與波浪相關(guān)的正反饋和海溫冷卻引起的負反饋之間的平衡決定的。Warner等[18]基于WRF-ROMS-SWANSediment transport耦合模式對臺風“Isabel”的海氣交換及泥沙輸移進行模擬，發(fā)現(xiàn)海洋與大氣的耦合會導(dǎo)致邊界層應(yīng)力降低，而波浪與大氣的耦合則會導(dǎo)致底部應(yīng)力增加。已有研究為海上結(jié)構(gòu)抗風安全設(shè)計與防護提供了一定參考依據(jù)，但均忽略了海洋運動對臺風過境全過程時空水平風速特性的影響。

鑒于此，本文采用中尺度WRF模式、第三代海浪模式SWAN與有限體積海流模式FVCOM構(gòu)建臺風-波浪-海流實時耦合模擬平臺，模擬分析了臺風“莫蘭蒂”過境全過程水平風速特性，同時與非耦合WRF模式的模擬結(jié)果進行對比，分析得到了海洋運動對于臺風水平風速的影響，為海洋大氣數(shù)值模型建立與海上風電場結(jié)構(gòu)設(shè)計提供參考依據(jù)。

1 臺風-波浪-海流耦合模擬

1.1 數(shù)值模擬方法

1.1.1 中尺度大氣模式WRF

WRF大氣模型[19]是美國國家大氣研究中心、美國國家海洋和大氣管理局等聯(lián)合開發(fā)的新一代中尺度天氣預(yù)報系統(tǒng)。本文采用的WRF-ARW（研究模式）動力框架基于完全可壓非靜力平衡歐拉方程，水平方向上采用Arakawa C網(wǎng)格劃分，垂直方向上采用靜力氣壓地形追隨坐標。

模式的近似通量形式歐拉控制動量方程組為：

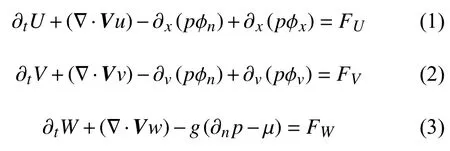
式中：u、v、w分別為水平方向x向速度分量、水平方向y向速度分量、垂向速度分量；U、V、W分別為水平方向x向動量分量、水平方向y向動量分量、垂向動量分量；FU、FV、FW分別表示由物理過程、湍流混合、球面投影造成的力源項。

1.1.2 第三代海浪模式SWAN

SWAN海浪模型[20]是由荷蘭Delft大學開發(fā)的第三代近岸海浪模型，具有模擬海洋風浪、涌浪及混合浪的能力。SWAN模式采用基于Euler近似的波作用動譜平衡方程作為描述海浪的控制方程，方程在笛卡爾坐標系下表達式為：

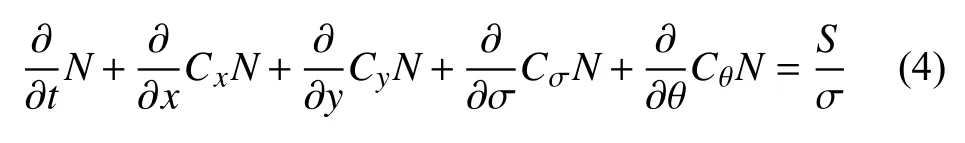
式中：N為波浪作用譜密度；Cx、Cy、Cσ、Cθ分別為x、y、σ、θ四個方向上的波浪傳播速度；S表示能量的源匯項，其中包括了風能的輸入、能量的耗散以及波浪之間的非線性相互作用。

1.1.3 有限體積海流模式FVCOM

FVCOM海洋模型[21]是由美國麻省理工大學和伍茲霍爾海洋研究所聯(lián)合開發(fā)的適用于三維水動力模擬的有限體積海流模式。FVCOM模型在笛卡爾坐標下的三維動量方程為：

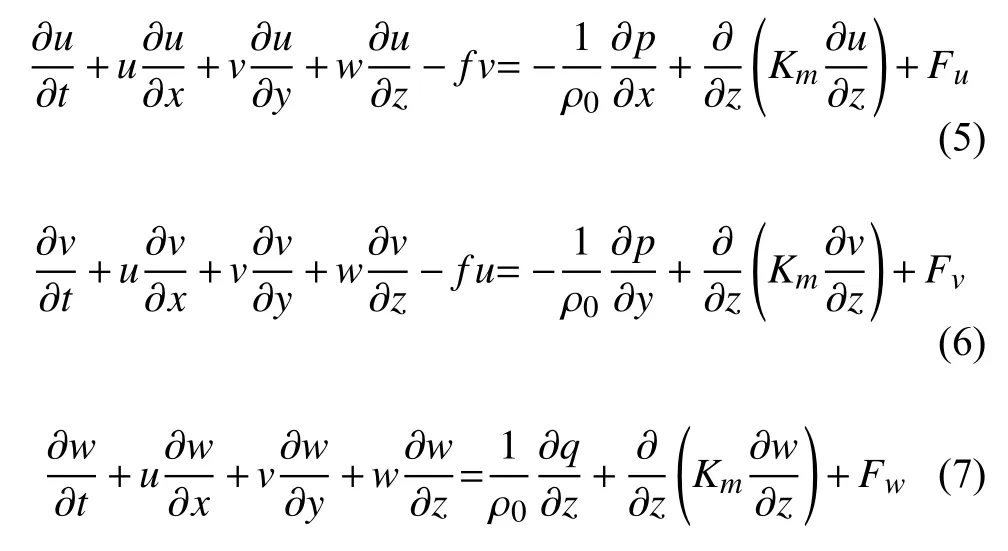
式中：x、y、z分別為笛卡爾坐標系三個方向上的坐標，u、v、w是三個方向上的速度分量，ρ為海水密度，ρ0為參考密度，f為科氏力參數(shù)，Km為垂向渦黏系數(shù)，F(xiàn)u、Fv、Fw分別為三個方向上的動量。

1.1.4 模型耦合機制

W-S-F耦合模擬平臺由主程序調(diào)用各子模型同時獨立計算，各子模型調(diào)用MCT子程序進行數(shù)據(jù)的實時交換。模型耦合機制如圖1所示。其中，WRF向SWAN和FVCOM傳遞風速驅(qū)動海洋運動；FVCOM向WRF傳遞海表溫度，向SWAN傳遞海流潮位和流速；SWAN向FVCOM和WRF分別傳遞影響海流運動和臺風發(fā)展的波形要素。

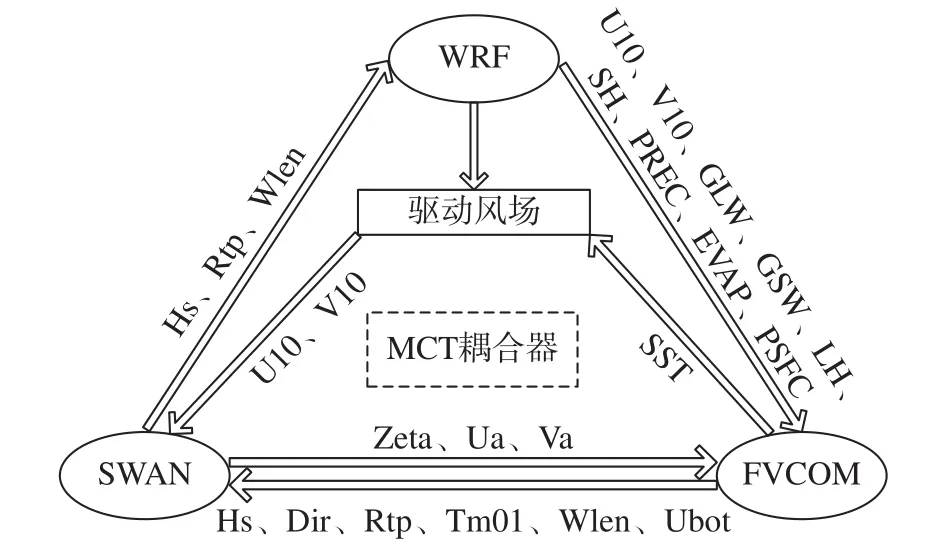
圖1 W-S-F模型耦合機制示意圖Fig.1 A diagram of the W-S-F coupling mechanism

1.2 臺風“莫蘭蒂”模擬

臺風“莫蘭蒂”（Meranti，國際編號：1614）于2016年9月10日14時在西北太平洋洋面上生成，11日14時加強為強熱帶風暴，12日11時繼續(xù)加強為超強臺風，13日晚間加強到頂峰（此時風速62 m/s）。此次臺風于9月15日以強臺風級在福建省廈門市登陸，登陸時中心最大風力35 m/s。為分析波浪與海流對臺風過境全過程水平風速特性的影響，本文設(shè)計兩組工況：1）非耦合WRF模式模擬未考慮海洋作用的臺風運動；2）W-S-F耦合模擬海洋與大氣實時傳遞作用的臺風運動。控制兩組工況下的模擬計算區(qū)域及WRF的設(shè)計參數(shù)完全一致，WRF的物理化參數(shù)方案及模擬計算域內(nèi)波浪、海流網(wǎng)格劃分如表1所示。模擬計算時間為2016年9月11日16時～2016年9月15日12時共92 h。WRF、SWAN、FVCOM三種模型的部分參數(shù)設(shè)置見表2。

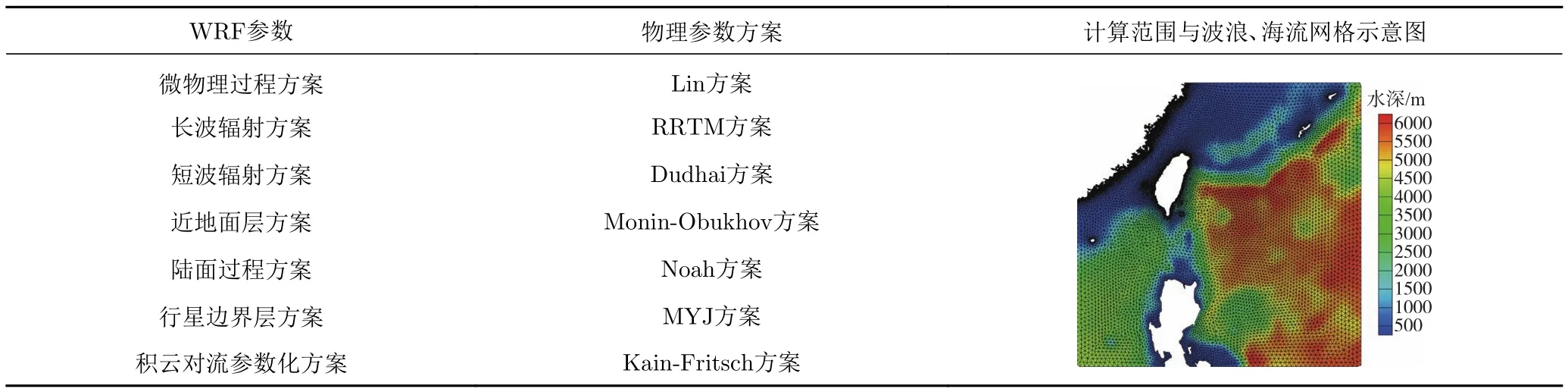
表1 WRF物理化參數(shù)方案及模擬計算域設(shè)置Table 1 Physical parameterization schemes of WRF and the setting of simulation computing region

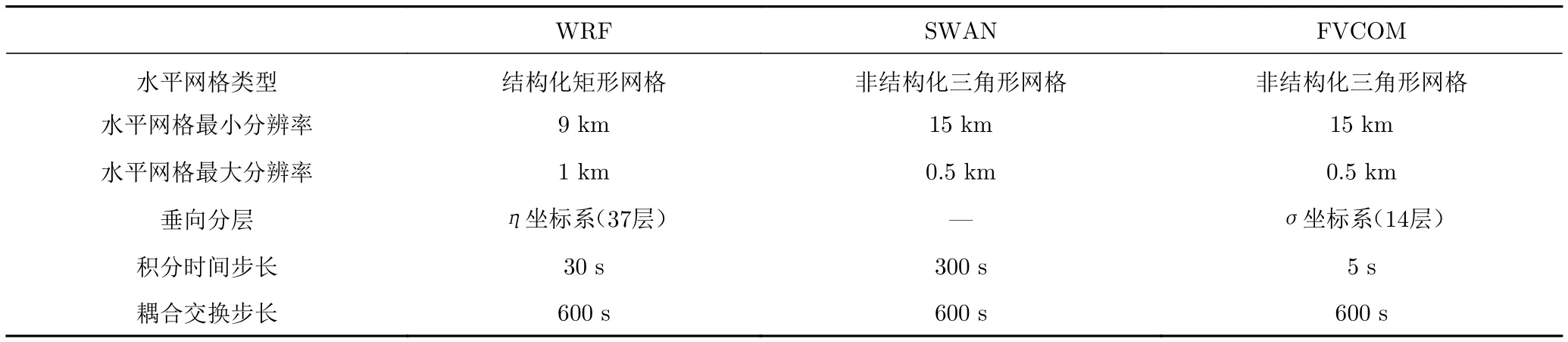
表2 W-S-F耦合模擬平臺參數(shù)設(shè)置Table 2 Parameters of the W-S-F coupling simulation

1.3 W-S-F耦合模擬有效性驗證

為驗證W-S-F耦合平臺數(shù)值模擬的有效性，以日本氣象廳東京區(qū)域?qū)I(yè)氣候中心JMA提供的臺風最佳路徑數(shù)據(jù)集[22]為參考，圖2給出了W-S-F耦合模式與WRF非耦合模式模擬的臺風路徑以及臺風中心附近最大穩(wěn)定風速誤差對比結(jié)果。由圖可知，整個模擬時間范圍內(nèi)，非耦合WRF模式與W-S-F模式模擬的臺風移動路徑比JMA最佳路徑均略偏北，W-S-F耦合模擬的臺風路徑比WRF非耦合模擬更接近JMA最佳路徑；兩種模式模擬的臺風中心附近最大穩(wěn)定風速在模擬期間先增大再減小，與JMA實測數(shù)據(jù)變化趨勢一致，W-S-F模式模擬效果全程優(yōu)于非耦合WRF模式。

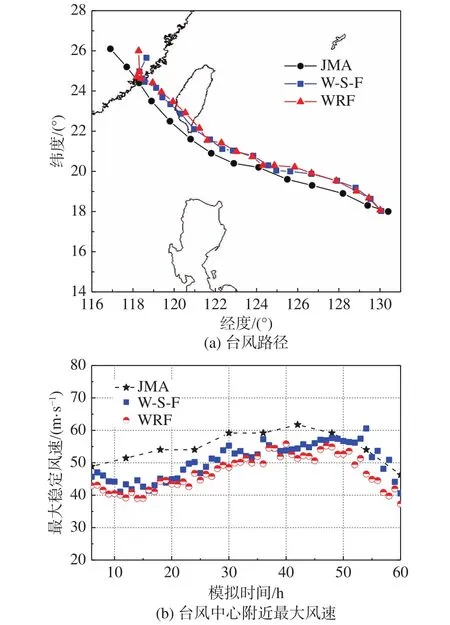
圖2 W-S-F耦合模式模擬結(jié)果有效性驗證Fig.2 The validity of simulation

1.4 W-S-F耦合模擬結(jié)果

圖3～圖5分別給出了在臺風“莫蘭蒂”10 m高度處風速矢量、有效波高以及表層流場云圖。

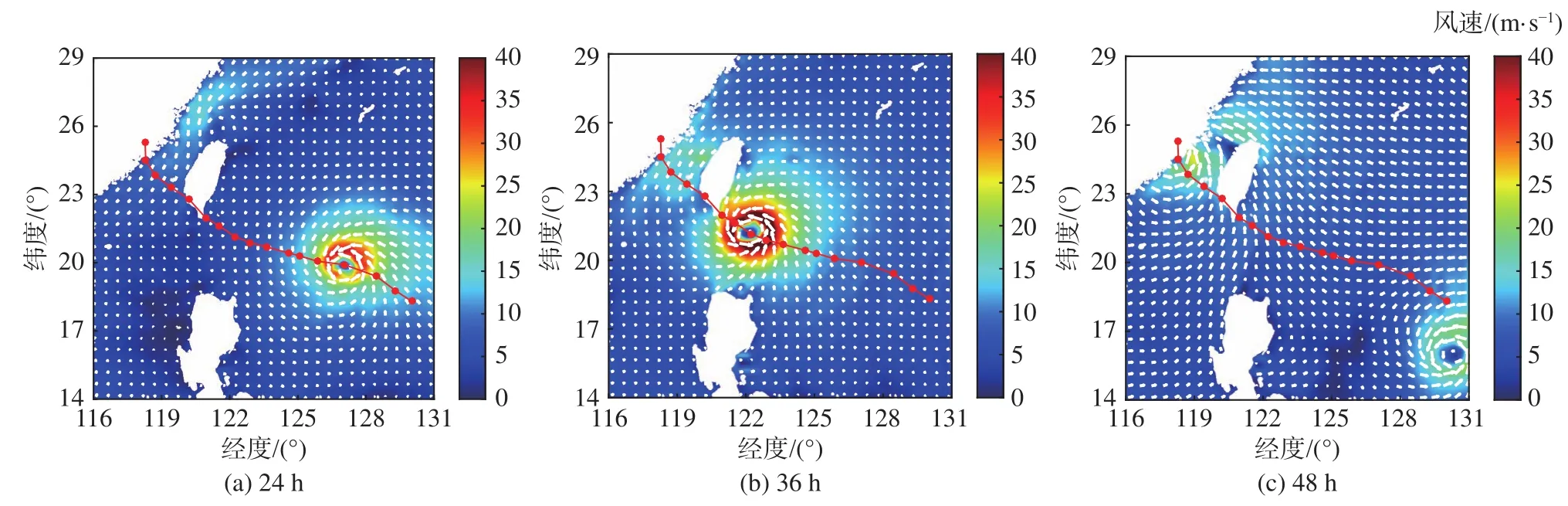
圖3 不同時刻風場模擬結(jié)果Fig.3 Numerical results of the wind fields at different time instants

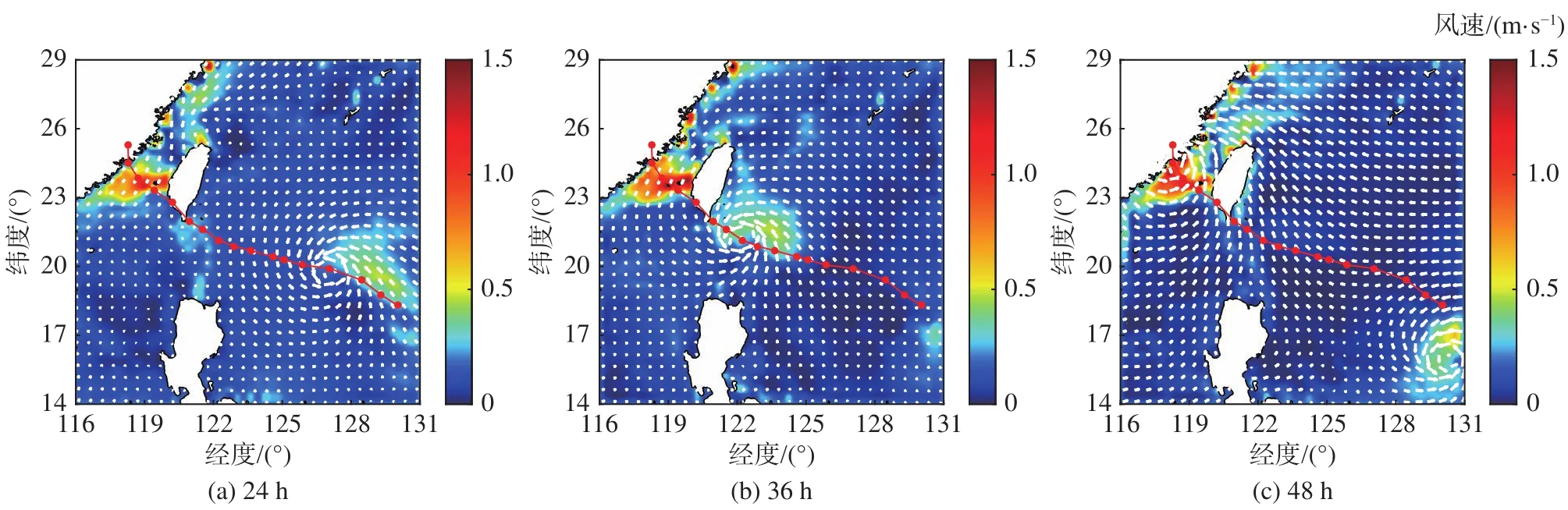
圖5 不同時刻表層流場模擬結(jié)果Fig.5 Numerical results of the surface flow at different time instants

由圖可知：1）臺風移動過程風速呈現(xiàn)非對稱分布，其中心右側(cè)風速明顯大于左側(cè)，臺風浪以及表層流場在空間上同樣呈現(xiàn)出“右偏性”的不對稱性分布特征；2）臺風作用下海域形成了明顯的旋轉(zhuǎn)波浪場，波浪場的旋轉(zhuǎn)中心位于臺風移動路徑的左側(cè)小浪區(qū)，其與表層流場對于臺風具有一定的滯后性，表層流場的滯后性較為明顯；3）臺風“莫蘭蒂”10 m高度處風速最高可達45 m/s以上，臺風中心附近形成有效波高10 m以上的狂濤區(qū)，表層流速在遠海區(qū)域達到1 m/s。

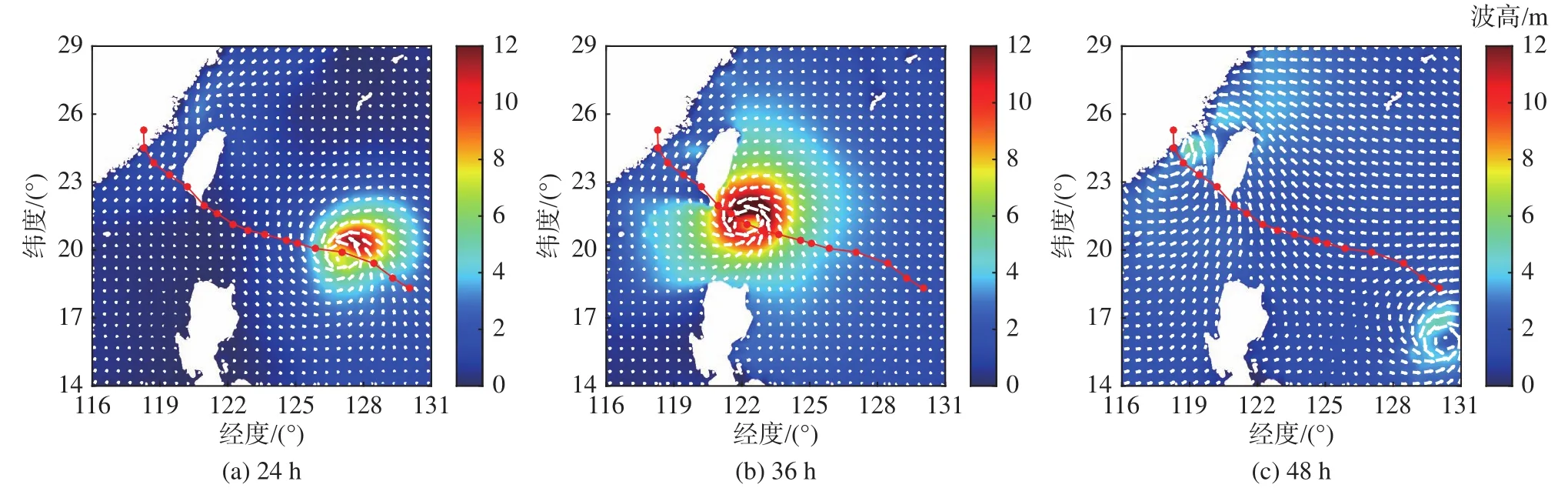
圖4 不同時刻有效波高模擬結(jié)果Fig.4 Numerical results of the significant wave heights at different time instants

2 海洋運動對臺風水平風速影響

2.1 臺風典型高度風速時程

圖6給出了臺風典型高度最大風速時程對比曲線，由圖可知，不同高度處臺風“莫蘭蒂”最大風速呈現(xiàn)先增大后減小的趨勢。海洋運動作用對于臺風在不同高度處的最大風速變化存在不同影響。

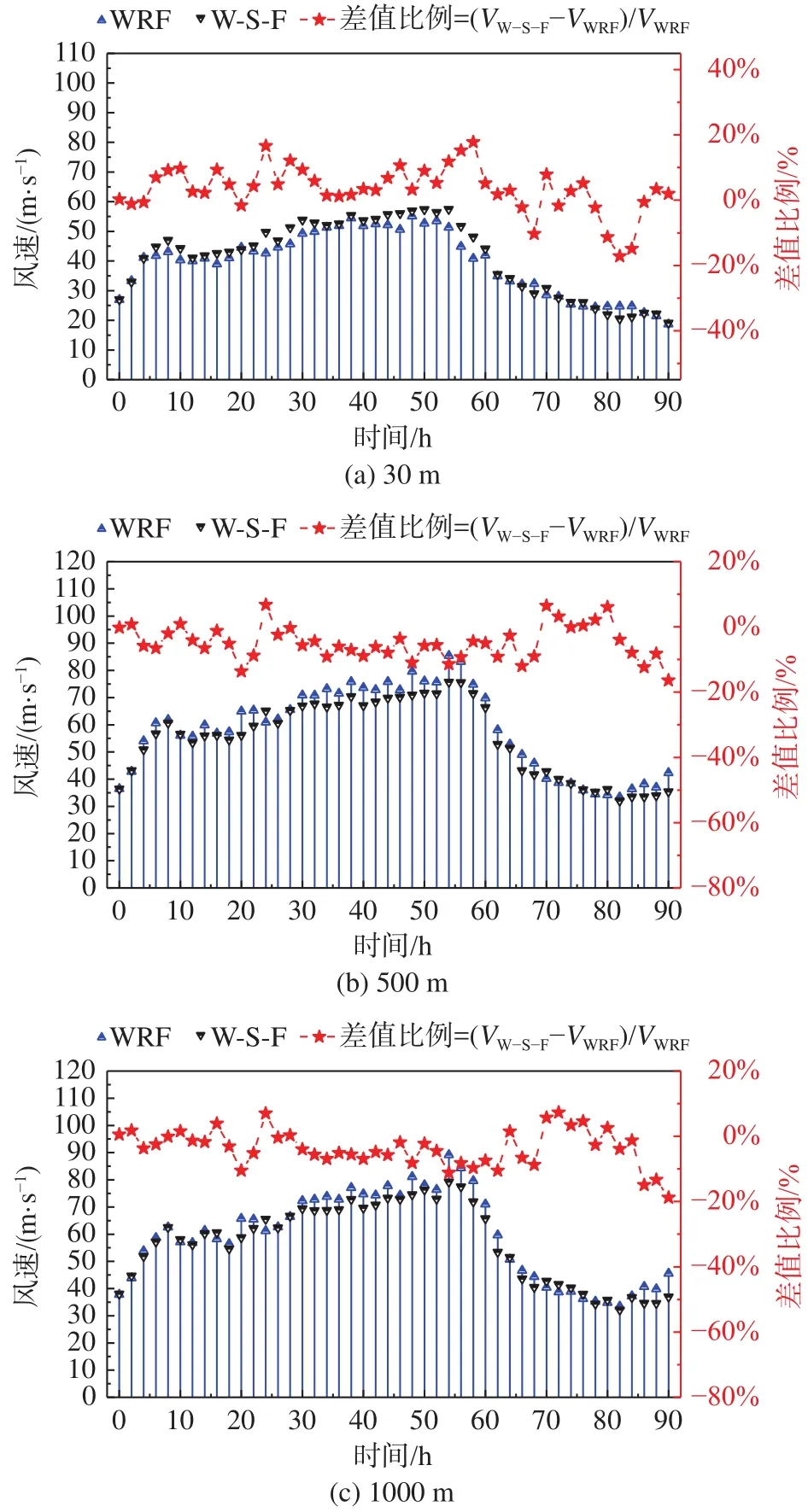
圖6 臺風典型高度最大風速時程對比曲線Fig.6 Time histories of the maximum wind speeds at typical heights of typhoon

在風速上升階段（0～45 h），海洋運動促進了低空臺風風速的發(fā)展，對高空臺風風速發(fā)展具有抑制作用。在強風階段（45～55 h），海洋運動對于高空處臺風發(fā)展的抑制作用更為顯著。在近海登陸過程中（55～92 h），海洋運動對大氣的影響隨著風速減小逐漸減弱。

產(chǎn)生這種差異結(jié)果的原因可能為：耦合模式考慮了復(fù)雜的大氣、海浪、洋流的相互作用與能量傳遞，在風速上升階段，風應(yīng)力的增加使上層海洋發(fā)生湍流混合，海氣熱量交換強烈。波浪破碎與能量耗散的升溫作用促進低空風速的發(fā)展；而隨著高度的增加，熱量耗散不斷累積，大氣能量減小，因而海洋運動對高空臺風風速產(chǎn)生一定的削弱。而在風速下降階段，海氣能量交換作用隨臺風強度降低而逐漸減小，海洋運動對大氣的影響也隨之減弱。

2.2 臺風三維風速分布

圖7和8分別給出了兩組工況下臺風登陸時刻典型高度截面水平方向風速隨經(jīng)度及緯度的三維分布圖。從圖中可以看出：在不同高度處，兩種工況下的三維風速分布情況基本一致，且均具有明顯的臺風眼結(jié)構(gòu)。登陸期臺風強度不斷削弱，海洋運動使得臺風登陸期發(fā)展較快，以致臺風水平向風速較小且起伏更為平緩。

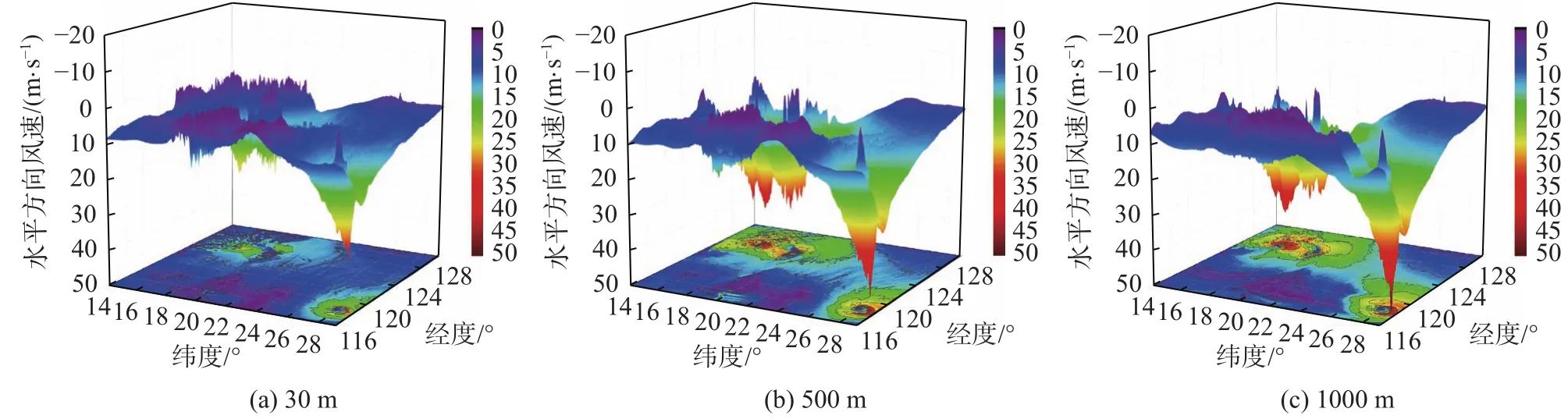
圖7 W-S-F耦合模式臺風風速分布三維云圖Fig.7 Three-dimensional nephograms of the wind speed distribution obtained by the W-S-F coupling model

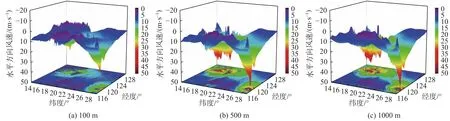
圖8 WRF非耦合模式臺風風速分布三維云圖Fig.8 Three-dimensional nephograms of the wind speed distribution obtained by the uncoupled WRF model

2.3 邊界層高度

圖9給出了臺風過境全過程的邊界層高度對比。由圖可知，WRF模式模擬的臺風影響全過程的邊界層高度平均值為566 m，耦合模式為692 m，海洋運動使得邊界層高度增大到約1.2倍。基于WRF模式臺風過境三個時期邊界層高度平均值分別為698 m、657 m和412 m，耦合模式下邊界層高度分別為755 m、943 m和619 m。

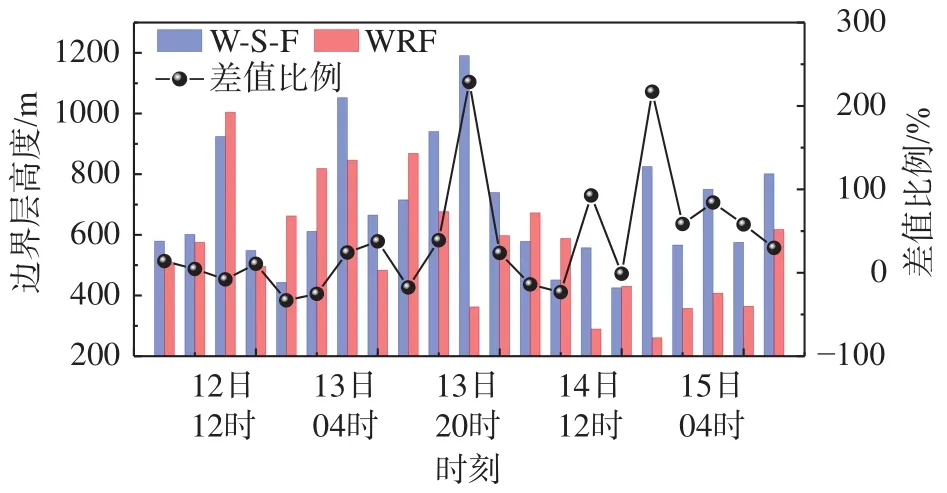
圖9 臺風過境全過程邊界層高度對比圖Fig.9 A comparison of boundary layer thickness throughout the typhoon landing process

與建筑結(jié)構(gòu)荷載規(guī)范（GB 50009—2012）[23]中A類地形的取值300 m相比，兩種工況下臺風各邊界層高度計算值普遍偏大，耦合模式下的邊界層高度最大值達到了規(guī)范值的3.4倍，非耦合模式最大值達到了規(guī)范值的2.9倍。

2.4 風剖面及指數(shù)時序規(guī)律

考慮臺風發(fā)展經(jīng)歷的穩(wěn)定上升期、強風期和登陸期三個階段，圖10給出了不同時期兩種工況下臺風結(jié)構(gòu)不同位置處的風剖面結(jié)果對比。其中，風剖面1～4分別位于臺風中心至臺風眼壁區(qū)域（風剖面1和2）、臺風眼壁區(qū)域（風剖面3）、臺風外圍區(qū)域（風剖面4）。風剖面指數(shù)與臺風眼距離的變化關(guān)系選取距臺風眼相同距離的所有模擬結(jié)果的均值。由圖可知，臺風風剖面擬合指數(shù)在各時期皆呈現(xiàn)隨著與臺風眼距離的增大而逐漸上升的趨勢，登陸期風剖面指數(shù)均值較登陸前明顯增大，海洋運動對臺風各個生命周期、同一位置處的風剖面均存在一定影響。風速穩(wěn)定上升期臺風眼區(qū)不考慮海洋運動的風速及風剖面冪指數(shù)更高，且靠近臺風眼壁區(qū)域差異較大，而臺風眼壁及以外產(chǎn)生相反的情況。臺風發(fā)展至強風期，海洋運動對臺風眼壁處風剖面擬合指數(shù)影響較大，較不考慮海洋運動情況下的差異最高可達0.04。在臺風登陸時期，海洋運動使得風剖面擬合指數(shù)隨著與臺風眼距離的增大變化更為強烈。

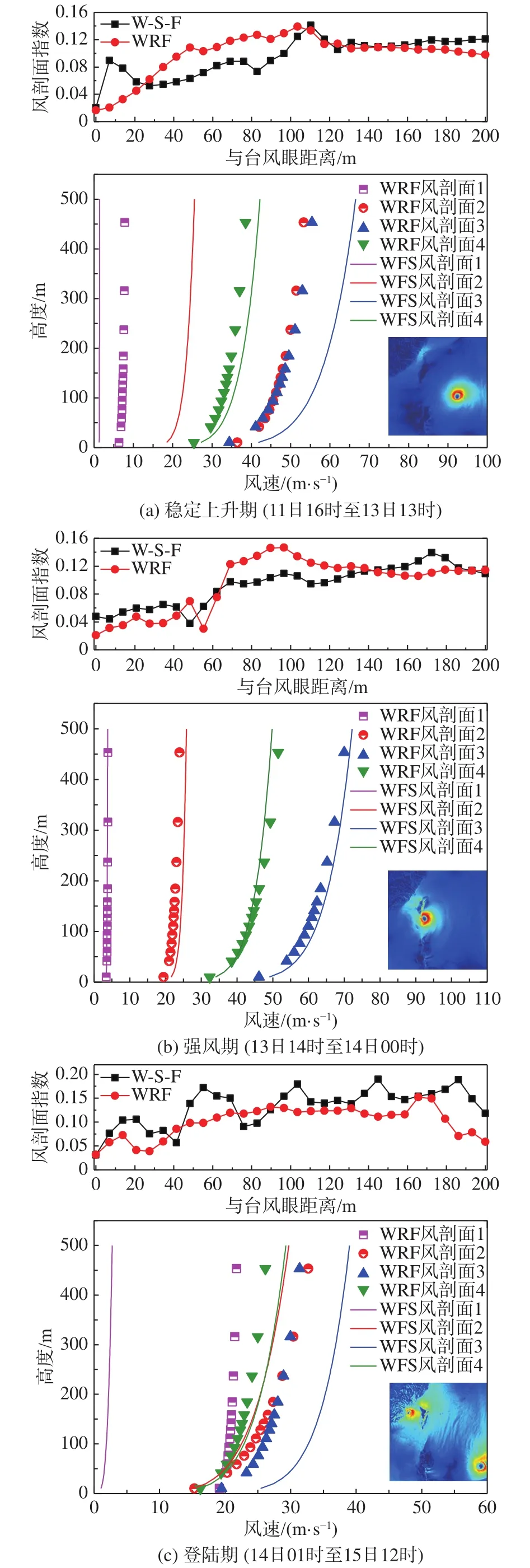
圖10 臺風不同時期兩種工況下風剖面模擬結(jié)果對比Fig.10 The comparison of numerical results of wind profiles under two working conditions at different stages of typhoon

圖11給出了臺風眼壁處風剖面冪指數(shù)時序圖，由圖可知，兩種工況下臺風眼壁處風剖面冪指數(shù)α隨時間的變化呈相反的趨勢，分別隨時間在擬合直線1（WRF）及擬合直線 2（W-S-F）的上下波動，臺風登陸前海洋運動對風剖面指數(shù)影響較大，并隨著臺風瀕臨陸地逐漸減小。臺風登陸后兩種模式下的風剖面指數(shù)基本位于0.1左右，海洋運動對其影響較為微弱。

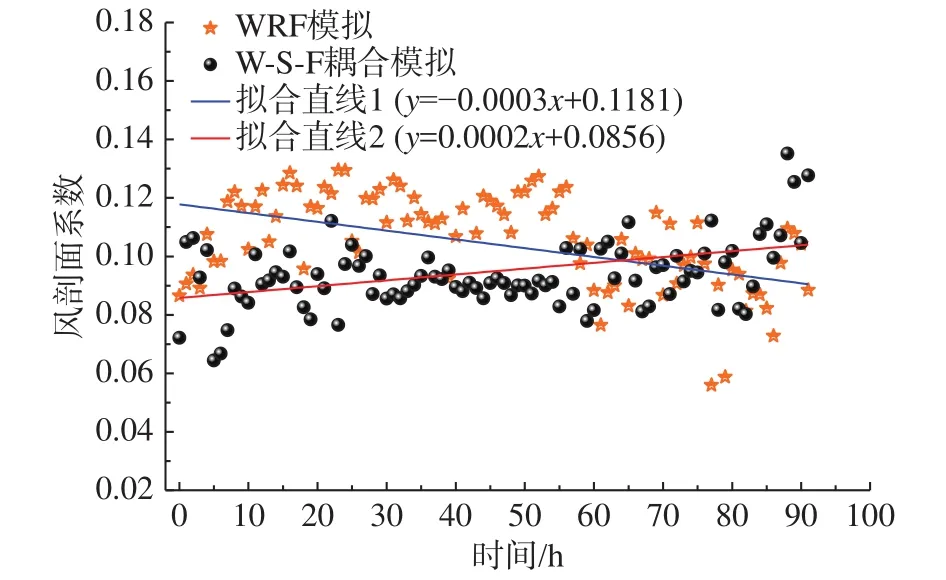
圖11 風剖面指數(shù)時序圖Fig.11 Time series of the power exponents of wind profiles

3 海洋運動對臺風水平風速影響時空規(guī)律模型

圖12以最大水平風速作為判定依據(jù)，給出海洋運動對臺風水平風速的影響隨高度與時間變化示意圖。其中，影響系數(shù)定義為海洋運動影響下臺風最大水平風速與不考慮海洋運動的臺風最大水平風速的比值。

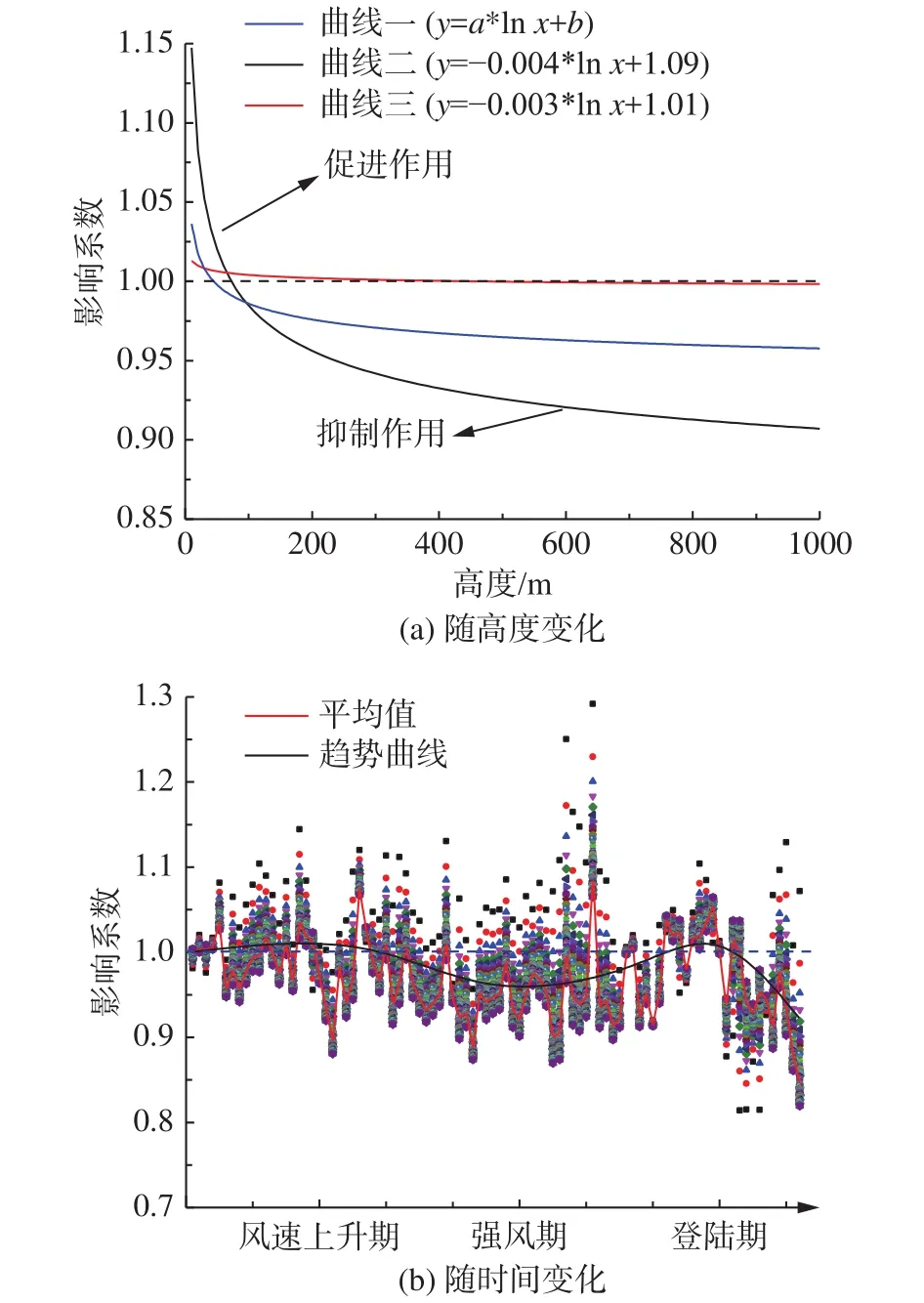
圖12 海洋運動對臺風強度影響隨高度與時間的變化Fig.12 Variations of the influences of ocean movement on the typhoon intensity with height and time

對比分析得到：

1）臺風發(fā)展過程中海洋運動對臺風強度的影響系數(shù)隨高度增大呈對數(shù)率減小。低空處海洋運動促進臺風強度，并隨高度增加影響逐漸減小。到達一定高度時，海洋運動對臺風強度產(chǎn)生抑制作用，且這種消耗隨高度增大而加強。

2）臺風不同生命周期其高度影響特性呈現(xiàn)不同程度的增減。風速上升期，海洋運動影響對于高度的敏感性逐漸增強，即隨高度變化影響程度逐漸增大。而登陸期，海洋運動的高度影響曲線隨風速減小而趨于平緩。基于此給出了海洋運動影響系數(shù)隨高度變化的對數(shù)模型：

式中：a代表海洋運動的高度影響程度，與風速值呈負相關(guān)；b代表海洋運動影響系數(shù)截距，與風速值呈正相關(guān)。

3）海洋運動對于臺風1 000 m高度范圍內(nèi)強度均值的影響隨臺風發(fā)展呈先促進后消耗，隨后消耗作用逐漸減弱后又不斷增強。結(jié)合海洋運動對于不同高度臺風的影響大小，可得到臺風發(fā)展過程中各個時刻與高度受海洋運動的作用程度。

4 結(jié) 論

本文基于MCT耦合器，通過中尺度WRF大氣模型、三維水動力FVCOM模型以及第三代淺海海浪SWAN模型建立了大氣-海洋-海浪的實時耦合平臺，分析了海洋運動對臺風過境全過程水平風速特性的影響規(guī)律。研究表明，本文提出的W-S-F耦合平臺可以準確模擬考慮海洋運動的臺風過境全過程風速場，且海洋運動對臺風過境全過程水平風速的影響不可忽略。

兩者相互作用和影響機理闡述如下：海洋與大氣通過熱量傳遞、摩擦阻力、氣壓變化等能量交換過程相互促進、相互消耗。低空處海洋運動能促進臺風強度，隨高度增加影響逐漸減小；高空處海洋運動對臺風強度產(chǎn)生抑制作用，且這種消耗隨高度增大而加強。在臺風整個發(fā)展周期，海洋運動對低空臺風強度的影響呈現(xiàn)先促進后抑制規(guī)律，隨著高度增加逐漸形成相反特點。海洋運動使得邊界層高度顯著增大，可使邊界層高度平均值最大放大到1.2倍。