全局方向模板在高階精度非結構有限體積方法中的推廣

孔令發，劉 偉，董義道

(國防科技大學 空天科學學院，長沙 410073)

0 引 言

相比多塊結構化網格和笛卡爾網格，非結構網格因其便捷靈活的生成方式，近年來逐漸成為CFD研究與應用的熱點[1-4]，但伴隨著非結構網格的廣泛使用，一個涉及網格生成和模擬精度的矛盾開始變得愈發突出[5-6]。因此，學者們不斷嘗試改進基于非結構網格的離散算法，來實現自動化網格生成與精準化數值模擬的統一。

目前，針對非結構網格較常用的數值方法是具有二階精度的有限體積方法[7-10]，該方法因具有較好的數值表現而被應用于很多知名商業軟件，如ANSYS公司開發的商業軟件Fluent，以及NASA開發的In-house軟件FUN3D等[11]。為了提高計算效率與流場分辨率，很多學者嘗試將此數值方法向更高精度推廣[12-16]。不同于二階精度，高精度非結構有限體積方法的實現，除了需要引入更多的高斯積分點來實現高階精度通量積分外，還需要重構控制體單元的高階導數。有關高階導數的重構，Barth與Jespersen[17-18]首先提出了k-exact重構算法，Ollivier-Gooch等[19-21]在此基礎上發展了具有高階精度的非結構有限體積離散方法，并系統研究了有關高階精度非結構FV離散的對流、粘性通量與源項積分過程，以及曲線邊界處理等一系列問題。

在高階離散中，不同模板對實際計算（尤其是梯度與高階導數重構過程）具有更直接的影響，因此部分學者也開展了相應的模板選擇研究。文獻[11]提出了一種“智能增加”(Smart Augmentation, SA)模板構造方法。在共面模板的基礎上，從圍繞中心單元每個節點的共點模板中尋找了一個距離中心單元最近的單元。該方法完全基于距離信息，可能導致流場出現非物理解。為了克服這一問題，在SA模板的基礎上，Schwoppe等[11]繼續從共點模板中選擇單元，以改善最小二乘矩陣的條件數。Nishikawa在文獻[22]研究指出，盡管該方法帶來了一定程度的改進，但在高度變形網格上其計算穩定性較差。為克服這一問題，Nishikawa同樣基于共面模板增加額外單元，其中一個是通過增加額外單元改進模板的對稱性；另外一種以減小最小二乘矩陣系統Frobenius范數的倒數為目標，從而降低重構梯度的數值，以提高數值模擬的穩定性。但遺憾的是，這一模板構造方法在一定程度上降低了數值模擬的離散精度。

不同于上述模板選擇方式，Xiong等[23-24]針對二階精度非結構有限離散，提出了一種基于局部方向的模板選擇方式，使得模板選擇沿著兩個局部方向依次進行。這種模板選擇方式在非結構網格上初步體現出類似結構網格的結構化特征，易于并行，并且在各向同性的三角形網格上，其中一個局部方向接近壁面法向，另一個方向沿著流向，比較有效地反映了例如邊界層型流場的主要變化情況。但在高度各向異性三角形網格上，由于其中一個局部方向與偏離壁面法向間偏差相對較大，導致其穩定性下降[24]。

在局部方向模板的基礎上，本文作者在前期工作中探索了一種基于計算域全局方向的模板選擇方法[25]。例如邊界層型流動，由于沿著壁面法向的變化相對劇烈，于是希望重構過程的模板單元能夠盡可能多地體現壁面法向的流動信息。因此，其中一個全局方向可取當地壁面法向，同時為了使模板具有更好的空間延展性，并保留結構化特征，另一個方向可取流向。相比上述幾種重構模板，全局方向的確定更加簡便，擺脫了原始網格拓撲對模板構型的影響，并且能夠準確反映流場特征。在二階精度非結構有限體積方法中，其計算誤差相比常用的共點與共面模板更低，并且所需的模板數量較少，在具有較高計算準確性的同時，有效節約了計算開銷。

本文將全局方向模板推廣至具有三階精度非結構FV求解器，以測試其在高階精度數值模擬中的計算效果。文章的總體結構如下：第1節給出了高階精度非結構有限體積方法的控制方程離散以及kexact重構的基本過程；第2節主要討論了不同的模板選擇方法，并敘述了全局方向模板選擇方法的主要思想與基本過程，簡要探討了在相對復雜的外形上確定全局方向的基本思路；第3節分別測試了全局方向模板在兩類數值算例中的表現情況，同時測試了局部方向模板在高階精度非結構有限體積方法中的數值表現；第4節給出了本文結論與下一步工作展望。

1 非結構有限體積方法

1.1 控制方法與離散

無粘流動的積分型控制方程如下：

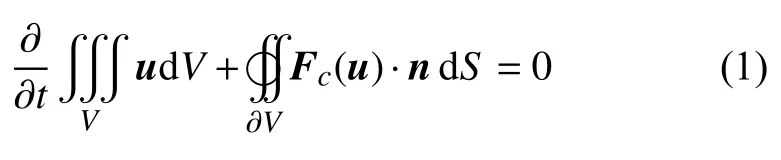
式中，u為守恒變量，Fc(u)為對流通量，n為控制體邊界面外法向矢量，V與?V分別代表積分域與積分域邊界。在高階精度FV離散過程中，方程(1)通常可被離散為：

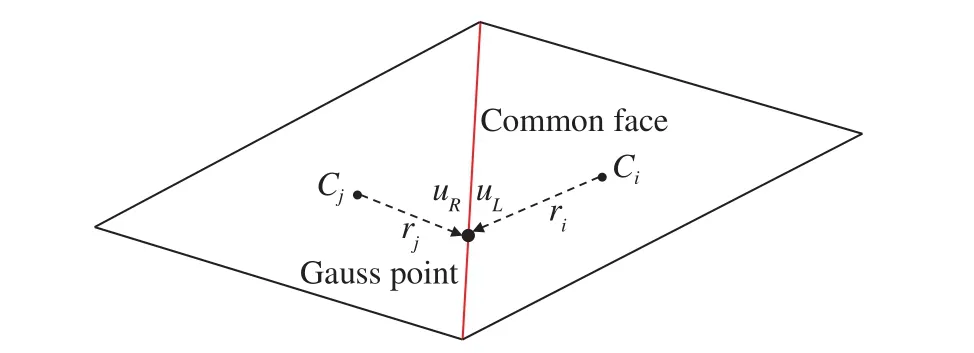
圖1 非結構有限體積高精度離散與通量構造示意圖Fig.1 Sketch of high-order unstructured finite volume discretization and flux construction

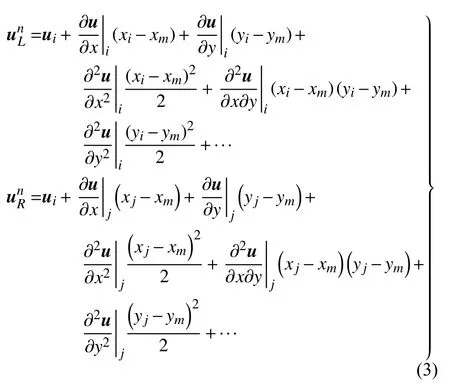
1.2 k-exact重構

在二階精度非結構有限體積方法中，通常采用最小二乘方法重構單元梯度，由于直接基于最小二乘方法進行泰勒級數展開無法達到二階以上精度，因此本節采用k-exact方法來實現單元梯度與高階導數重構。重構函數的形式如下：

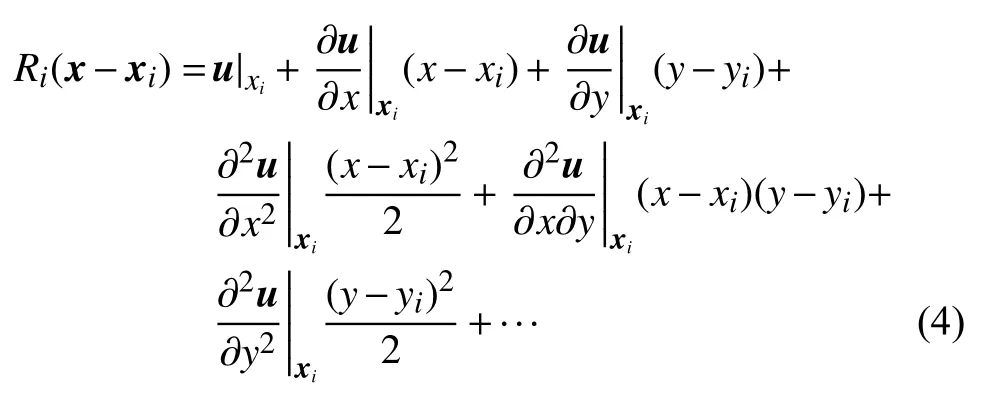
同時，其需要滿足的約束為：

因此，將重構函數在單元j上積分可得：

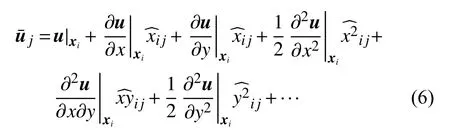
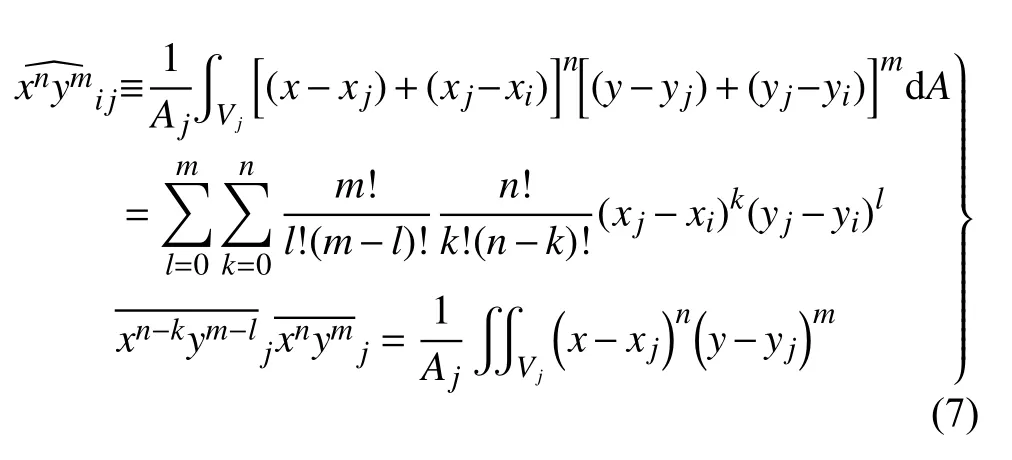
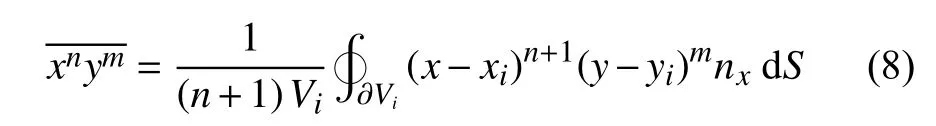
式中nx為單元面單位外法矢量的x分量。

參照方程(6)，針對任意模板單元均可構造一個重構多項式，并最終組建矩陣方程組：

方程組的第一個方程是約束方程，除約束方程外，其余每個方程前均乘以權系數 ωij：

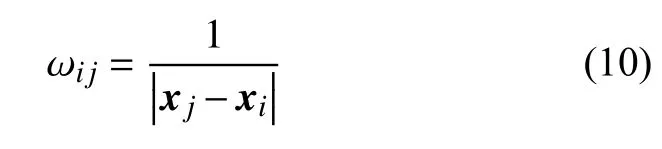
該系數用來強調與中心控制體幾何上鄰近的模板單元對重構結果的影響。在得到單元梯度與高階導數的基礎上，可通過約束方程得到單元變量點值：

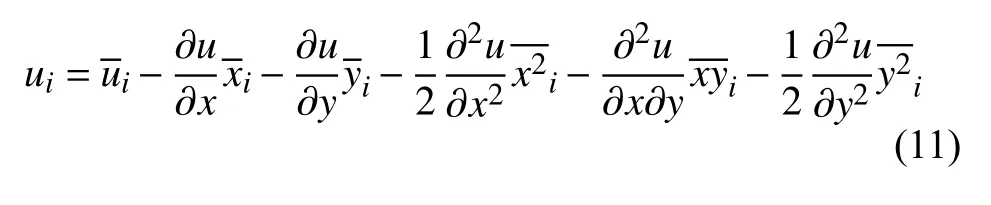
該點值用來插值計算單元面高斯點處的左右狀態矢量，以構造該點處的數值通量。

2 模板選擇方法

本節回顧了當前應用廣泛的共點、共面模板以及局部方向模板選擇方法的基本思路與存在的問題，并在此基礎上，給出了全局方向模板選擇方法的具體過程及其表現效果。

2.1 共點與共面模板

共點模板以及共面模板的應用最為廣泛，其依賴于網格拓撲，并通過相應的模板層數來控制模板單元數量使其滿足重構方程的要求，如圖2所示，共面模板由于網格單元面數量固定，因此隨著模板層數的遞增，模板單元數量增長平緩，而共點模板的數量較難控制，并且隨著層數增加，單元數量快速上升。

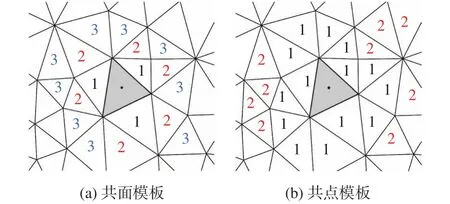
圖2 共面模板與共點模板Fig.2 Face-neighbor and vertex-neighbor stencils

此外，兩種模板選擇方式均依賴于固定的網格拓撲關系，針對不同流動無法有效捕捉到流場變化，并且兩種模板在滿足重構要求的基礎上，包含過多冗余單元，尤其是進行高階導數重構時，所需要的模板數量較多，因此隨著層數的增加，冗余單元的數量也因此驟增，這將顯著增大計算開銷，降低求解效率。

2.2 局部方向模板

針對上述兩種模板存在的問題，Xiong等[23-24]構建了基于兩個局部方向的模板選擇方法，這種模板選擇方法有效減少了用于重構的模板單元數量，并且在各項同性或長寬比較小的三角形網格上，兩個局部方向近似沿著壁面法向與流向，在二階精度非結構有限體積求解器中取得了較好地數值表現。

如圖3所示，對于四邊形單元，局部方向就是網格單元兩組對邊中點的連線；在處理三角形單元時，可將三角形單元的一個頂點視作由四邊形的一條邊退化而成，并將其稱為“退化點”，但由于存在三種可能的局部方向組合，因此需要采用陣面推進方法[26]（Advancing Front Technique, AFT）來確定最終的局部方向組合方式。

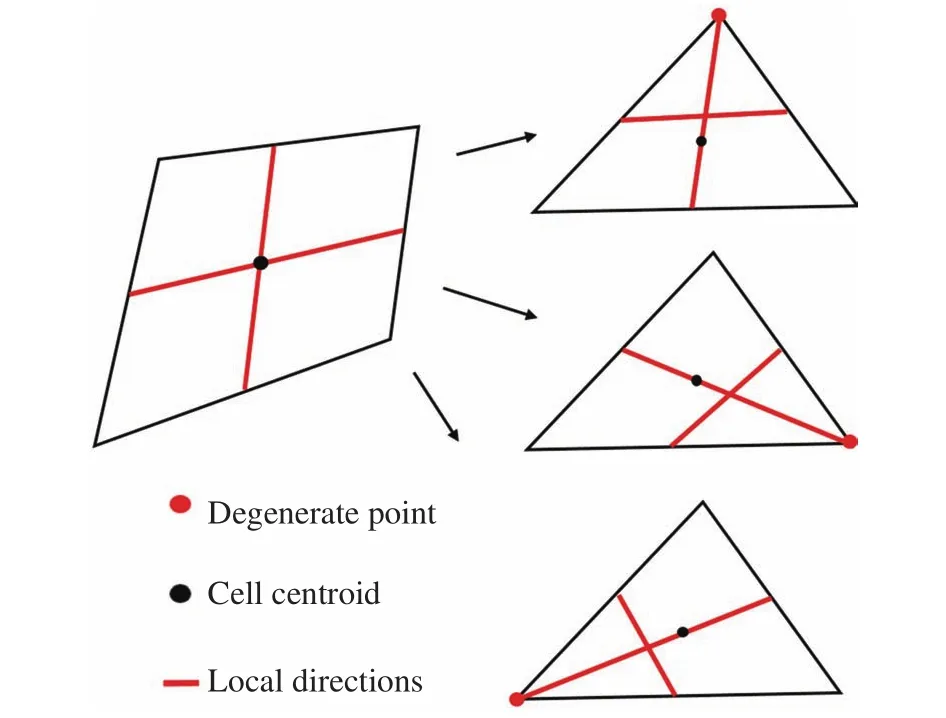
圖3 四邊形與三角形單元的局部方向組合Fig.3 Local directions of quadrilateral and triangular grids

針對三角形網格，基于陣面推進方法找到的局部方向的組合結果如圖4所示，從圖中可以看出，當網格長寬比較大時，其第一局部方向已偏離壁面法向。

圖4 三角形網格單元的局部方向組合Fig.4 Combination of local directions in a triangular grid

在確定局部方向的基礎上，可沿著兩個方向擴充模板單元。如果中心單元為四邊形，沿著局部方向選擇的模板單元實際上是共面模板單元。

圖5展示了三角形單元的模板構造方式。若局部方向通過“退化點”，例如圖中的P0點，此時選擇和局部方向夾角最大的單元；如果不通過“退化點”，則選擇相應的共面模板。由于該模板選擇方法涉及陣面推進與夾角判斷過程，相對增加了前處理過程的處理開銷。

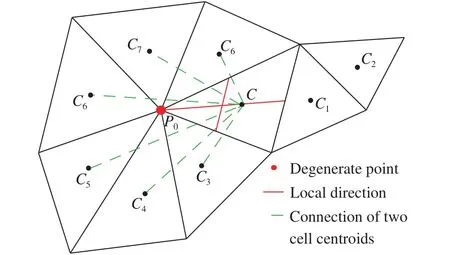
圖5 三角形網格的模板單元確定Fig.5 Stencil selection on a triangular grid

此外，如圖6所示，當網格長寬比較小時，局部方向模板單元基本沿著壁面法向與流向，但在高度各向異性網格上，由于局部方向的偏離，導致沿兩個方向找到的模板空間延展性下降。經測試，在此類網格上局部方向模板難以保證計算穩定性[24]。因此，針對這一問題，迫切需要發展一種新的模板構造方式，其能擺脫網格拓撲的約束，并準確捕捉流動的各向異性。

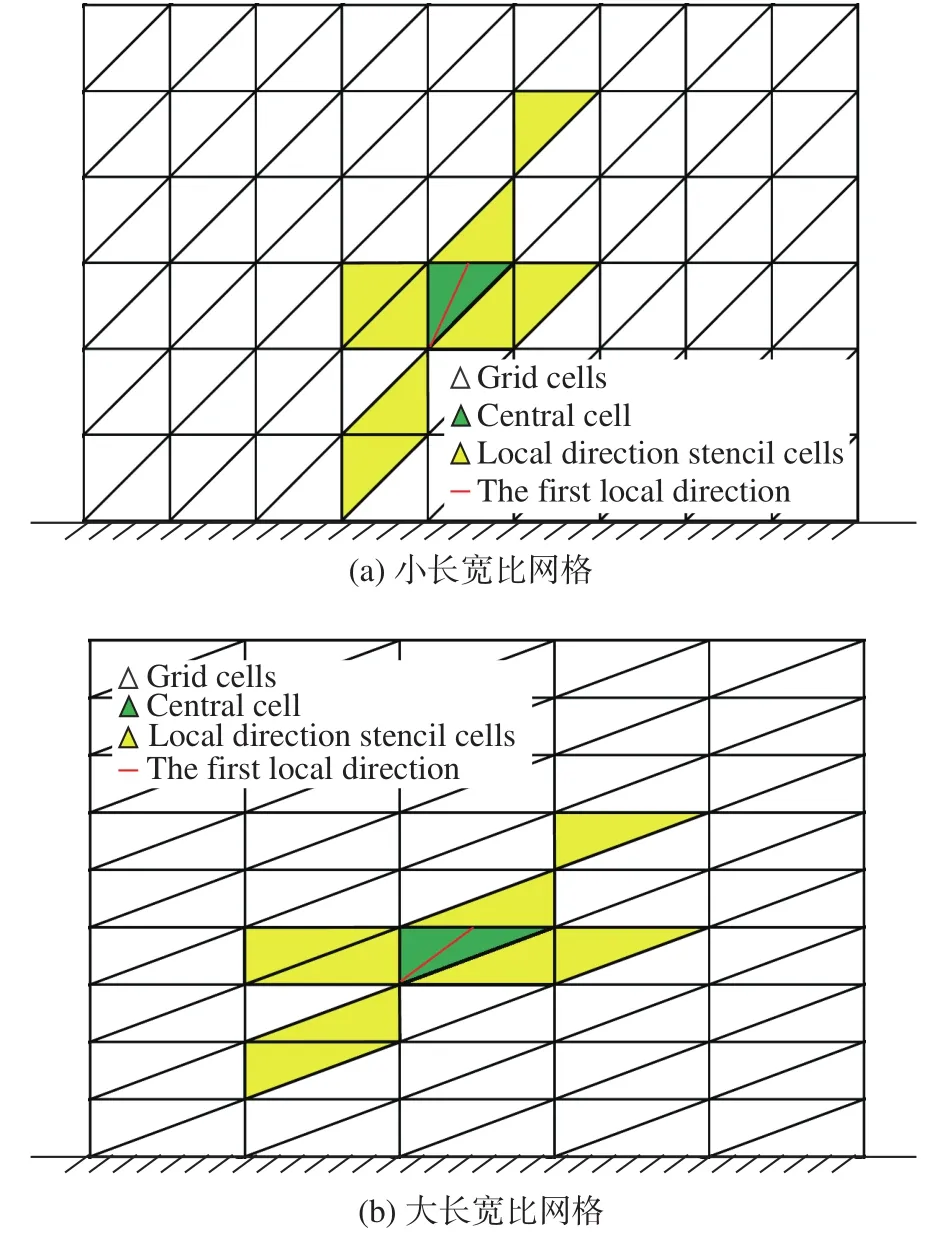
圖6 不同長寬比網格上的局部方向模板示意圖Fig.6 Diagram of local-direction stencils on grids with different aspect ratios

2.3 全局方向模板

在局部方向模板的基礎上，我們針對二階精度非結構有限體積方法發展了一種全局方向模板選擇方法，該方法不再依賴于每個網格單元內部的局部方向，而是計算域的全局方向。因此如圖7所示，即使在大長寬比三角形網格上，全局方向模板始終沿著壁面法向與流向，能夠準確捕捉到流場的各項異性特征。

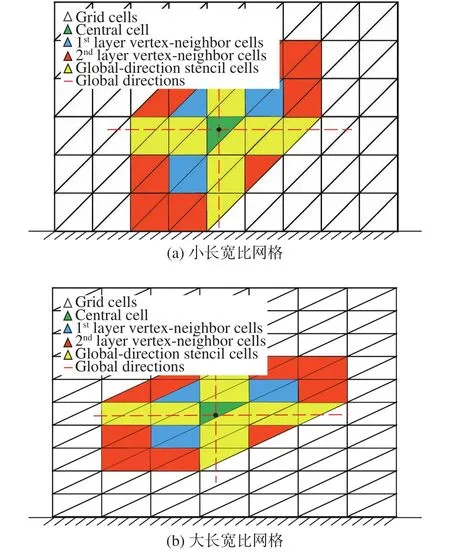
圖7 不同長寬比網格上的全局方向模板示意圖Fig.7 Diagram of global-direction stencils on grids with different aspect ratios

具體而言，尋找全局方向模板單元可分為兩個步驟，首先需要找到與中心單元共點的模板單元集合，在此基礎上，過中心單元的幾何中心做兩條直線，找到集合中與兩條直線相交的模板單元即可。因此，模板單元數量可得到較為準確地控制，并且整個過程并未引入任何復雜性。

針對簡單外形，確定壁面法向的過程相對簡便，例如圖7中給出的規則矩形計算域，其只包含一個壁面，確定全局方向時可直接取單元參考點處的壁面法向與切向。但對于更一般的外形，由于其物面不存在解析曲線，因此針對復雜外形確定計算域中單元參考點的全局方向時，可基于湍流模型中的壁函數計算首先獲得單元壁面距離[27-29]。在此基礎上，Jalali與Ollivier-Gooch[19]等提出了一種基于壁面距離來獲得壁面法向的有效手段，可采用該方法得到計算域中每一單元參考點處的壁面法向。此外，為使模板具有更好的空間延展性，另一個全局方向可取與壁面法向垂直的方向。

但在網格劃分好的前提下，對計算域中的每一個網格參考點計算一次壁面距離，并基于壁面距離確定壁面法向并不容易。這種處理方式會顯著增加算法復雜度與實現的困難程度，尤其在并行計算中。更重要的是，針對凹腔[30]這類局部包含多個壁面的情況，若在整個計算域內均采用全局方向模板，會造成方向判斷混亂，導致方法無法實施。

因此針對復雜外形，較好的處理方法是在對物面附近網格單元進行重構時，采用全局方向模板，來捕捉邊界層內部的流場變化，但在遠離邊界層的各向同性區域仍采用依賴網格拓撲關系的共點或共面模板。這樣做的好處在于，在邊界層內部可以有效捕捉流動的各向異性特征，并減少重構過程使用的模板單元數量；此外，針對凹腔等外形，考慮局域性后可保證方法的正確實施；同時，僅對物面附近的網格單元確定全局方向，可有效簡化算法的實現過程，并且在并行計算中的處理也會更加簡便。

本文首先在一些簡單外形上驗證了全局方向模板在高階精度非結構有限體積方法中的數值表現，為下一步將方法向復雜外形推廣打下了基礎。

3 數值驗證

為檢驗不同重構模板在高階精度非結構有限體積求解器中的數值表現，本節通過基于制造解方法(Method of Manufactured Solutions, MMS)[31-33]的流動以及超聲速渦流兩類數值算例，分別對比了共點、共面模板以及全局方向模板在三階精度求解器上的計算效果。由于2.2節分析了在各向異性的三角形網格上，基于局部方向找到的模板單元偏離壁面法向，導致其在二階精度求解器上，計算穩定性下降[23]。本節為了進一步檢驗局部方向模模板在高階精度非結構有限體積方法中應用的可行性，在測試上述三種模板計算效果的基礎上，還測試了局部方向模板的數值表現。同時，為簡化圖表中對不同模板的描述，我們分別使用 V-Stencil、F-Stencil、L-Stencil與 G-Stencil來表示共點、共面、局部方向模板與全局方向模板。

3.1 基于制造解方法的流動

本節針對歐拉方程構建了一個具有各向異性特征的MMS流動[34]，并且解的形式如下：

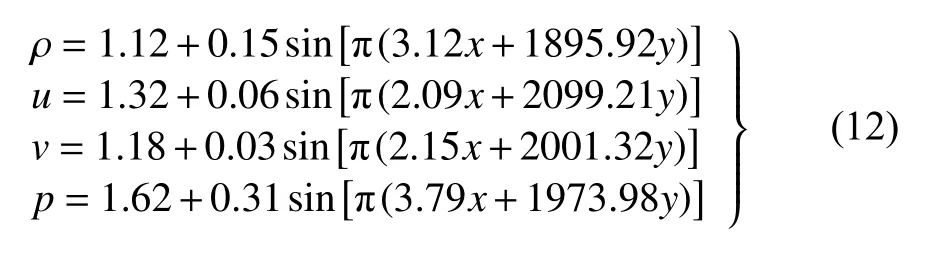
因此，可首先根據解的形式得到源項s為：

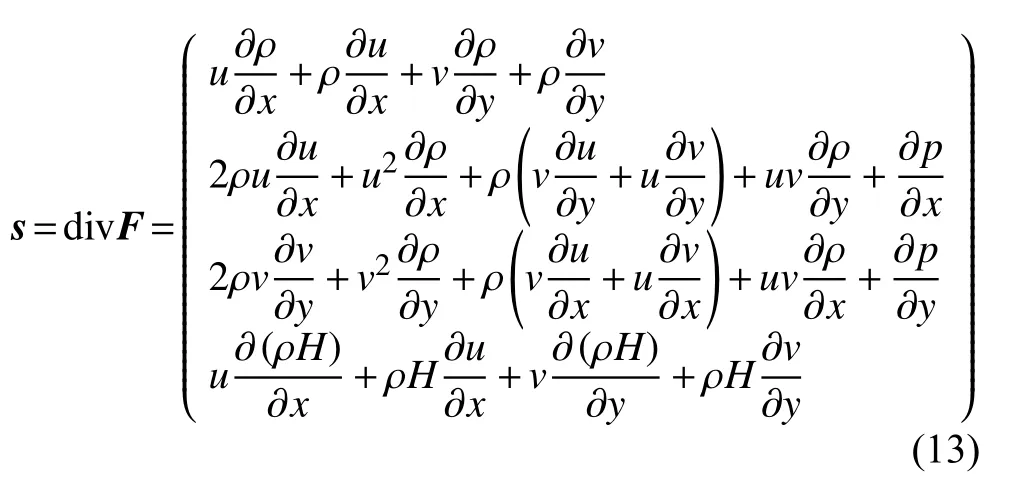
由于本文探討三階精度數值模擬中的不同模板選擇方法，如果僅采用單元中心處的源項點值，無法達到二階以上精度。因此需要對源項在控制體單元上進行數值積分，以保證其具有三階精度：

式中si與wi分別代表單元面中點處的源項與權系數，參照文獻[20]，wi可取由方程(10)得到的流場如圖8所示。

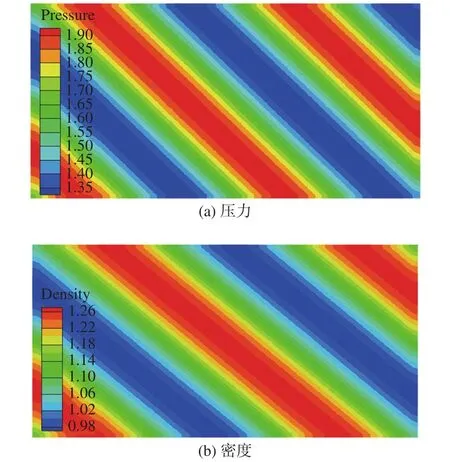
圖8 基于制造解的流場Fig.8 Flow fields with manufactured solutions

此外，我們分別測試了網格長寬比AR= 5×102、1×103的規則與擾動三角形網格，并且在每種長寬比下，分別設置了五套由疏到密的網格以測試不同模板的計算精度。網格示意圖與背景四邊形網格量分布如圖9與表1所示。

表1 不同長寬比下背景四邊形網格的分布量Table 1 The distribution of background quadrilateral grid cells with different aspect ratios

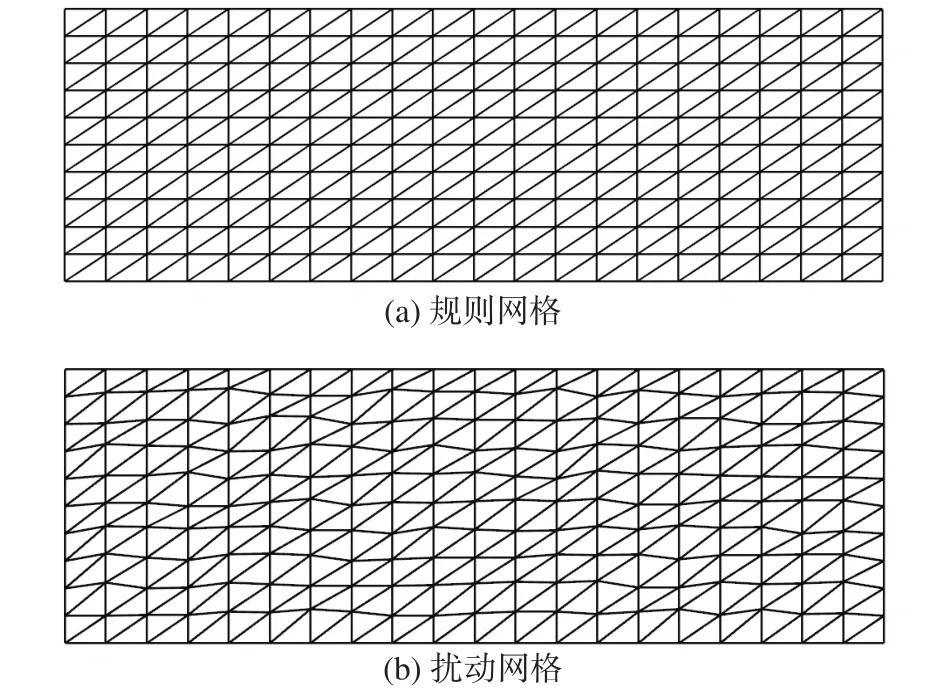
圖9 規則與擾動三角形網格Fig.9 Regular and randomly perturbed triangular grids

為簡化分析過程，并對比在高度各項異性網格上不同模板的表現，本節給出了長寬比AR= 1×103時的計算結果。但在測試過程中，我們發現局部方向模板在長寬比AR= 5×102與1×103的高度各向異性網格上計算發散。深入分析后發現，該方法在邊界附近找到的模板單元數量不足。

如圖10所示，對邊界單元C擴充模板單元時，首先可沿第二局部方向，找到與單元C共面的模板單元C2，其次在沿第一局部方向尋找模板單元時，由于第一局部方向與CC2之間的夾角小于CC1，進而沿第一局部方向找到的模板單元仍為C2，導致在邊界附近模板數量不足，需要不斷擴充層數以保證正確求解邊界單元的重構方程。因此后續的算例測試只給出了共點、共面模板與全局方向模板的計算結果。

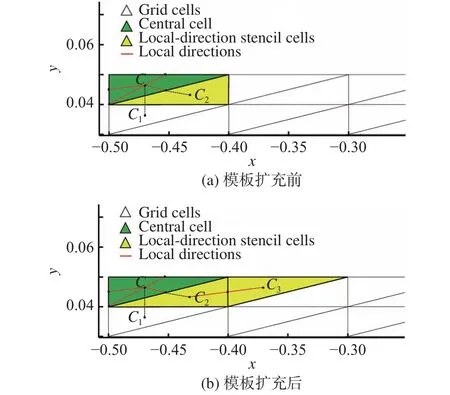
圖10 邊界附近的局部方向模板單元擴充Fig.10 The stencil augmentation of boundary-adjacent cells

從圖11與表2反映的計算結果來看，使用三種模板均能接近并達到求解器的設計精度，但在三種模板中，不論在規則網格還是添加隨機節點擾動的網格上，全局方向模板得到的計算誤差更低，因此，該模板的使用能夠有效改善求解器的計算準確性。

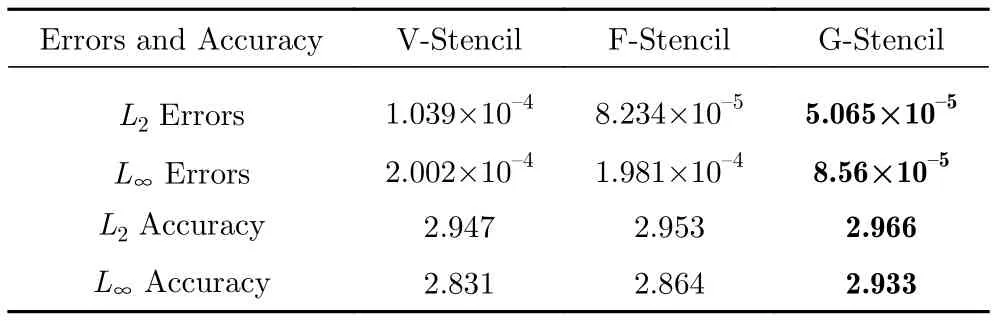
表2 規則密網格上的計算誤差以及最后兩套網格間的精度Table 2 Errors on the finest regular grid and computational accuracy between the last two sets of grids

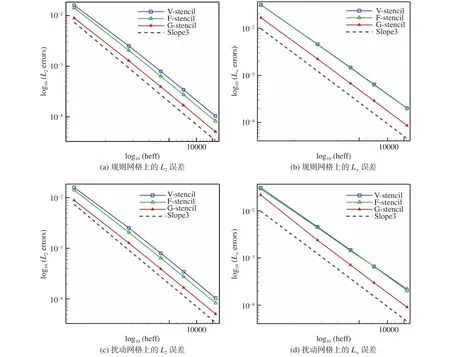
圖11 規則網格與擾動網格上的計算誤差Fig.11 Computational errors on the regular and perturbed grids

此外，由于三階精度非結構FV方法的重構過程需要求解6個未知量，因此，至少需要6個模板單元。但共點模板當層數取1時，在邊界單元上無法滿足重構方程組的求解，因此，需要將層數擴充為2，而共面模板只有當層數增加至4層時才可進行流場計算。結合圖12可以明顯看出，相比這兩種模板，全局方向模板所需要的模板單元數量更少，因此在具有更高計算準確性的同時，可相對降低重構過程的計算開銷。

圖12 三種模板的平均模板單元數量Fig.12 Average stencil sizes of three different stencils

但在上述對比中，三種模板選擇方式均是基于邊界處的模板單元數量而給定整體的模板層數，從而造成共點與共面模板的單元數量在整個流場中明顯增加。在此基礎上，我們僅對邊界單元擴充模板層數，而內部單元的層數保持最低，這樣可有效縮減三種模板的規模。

在長寬比AR= 1×103的網格上，通過上述方案得到三種模板的模板單元數量如表3所示。

為對比控制模板層數前后的計算誤差，兩種情況的誤差統計結果如圖13所示，并且修改層數后的模板選擇方法均添加標識“improved”。

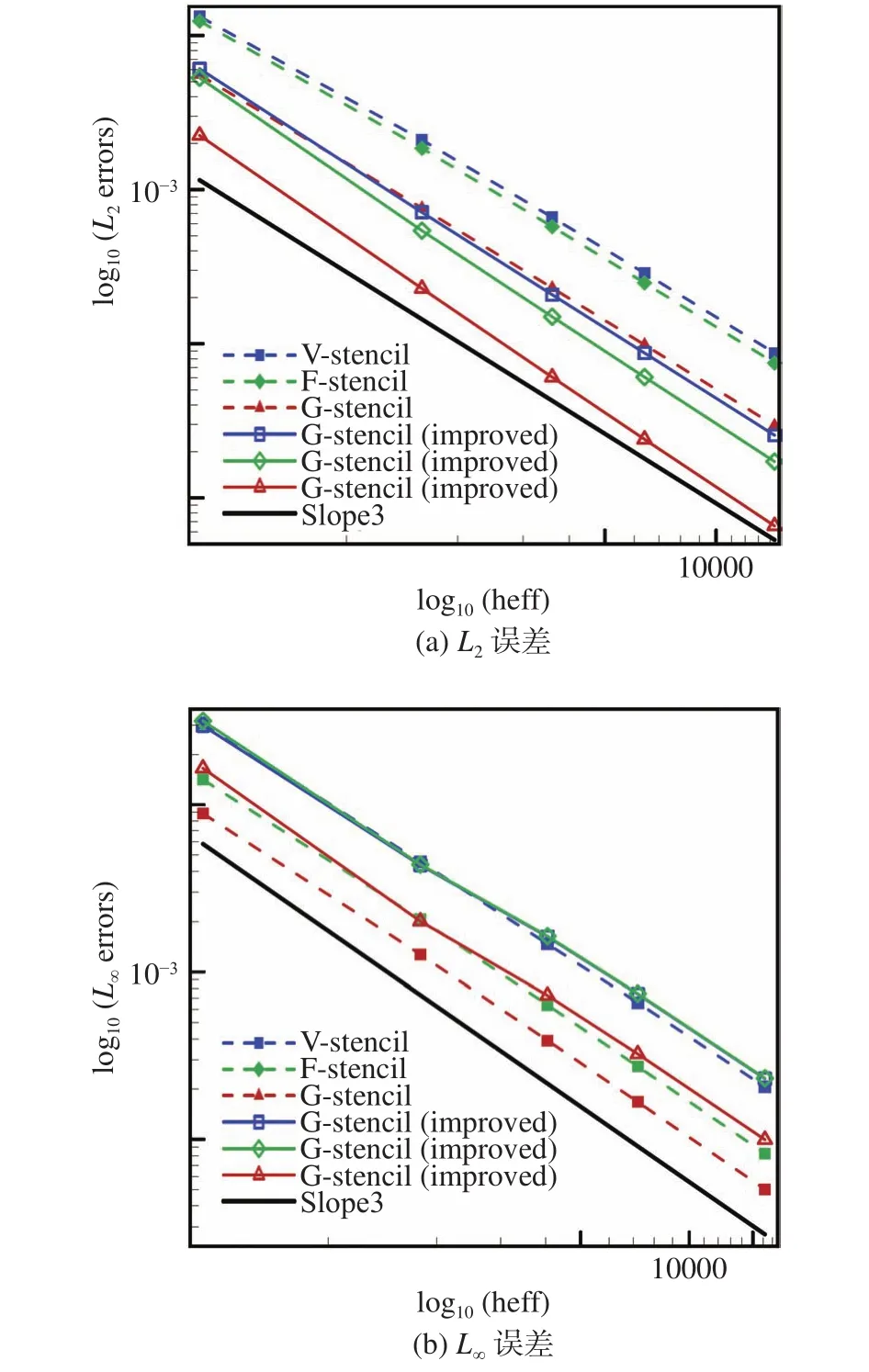
圖13 修改模板層數前后的計算誤差對比Fig.13 The comparison of computational errors before and after altering stencil layers

從圖中可以明顯看出，采用最小的模板層數后，三種模板的L2誤差均明顯降低，而L∞誤差相比縮減模板層數之前有所上升。但不論是否縮減模板層數，全局方向模板的誤差值在三種方法中均保持最低。同時結合表3中的數據可以看出，在對三種模板選擇方式縮減模板層數后，共點、共面模板，以及全局方向模板的模板單元數量均有所減少，但全局方向模板單元數量仍保持最少。因此，在模板數量差距較小的情況下，全局方向模板的計算誤差仍在三種方法中保持最低，有效證明了從完全多維的共點模板中提取具有分維特征的全局方向模板單元的必要性。

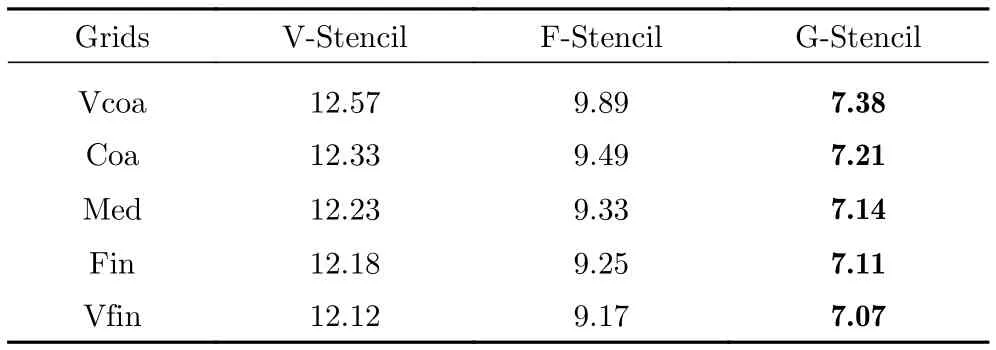
表3 三種模板選擇方式在不同網格上的平均模板單元數量Table 3 Average stencil sizes of three stencil selection methods on five sets of triangular grids

3.2 超聲速渦流動

本節采用含曲線邊界的超聲速渦流動，來進一步檢驗全局方向模板在真實流動中的數值表現。該流動具有解析解，其形式如下：

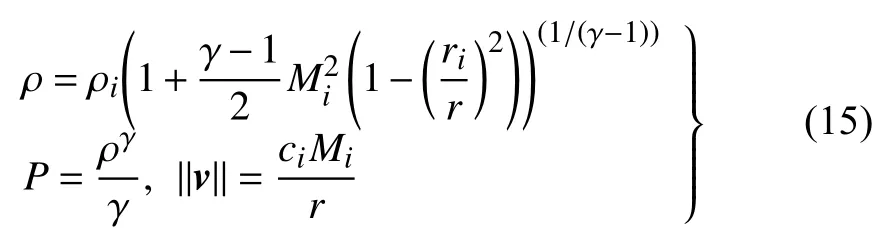
式中 γ為比熱比，‖v‖為速度的大小，并且其內外徑分別為ri= 1以及r0= 1.384。式中在內徑處的馬赫數Mi= 2.25，并且密度ρi= 1。此外聲速為：

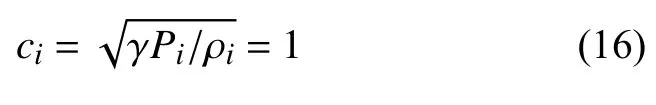
該流動的流場結構如圖14所示。

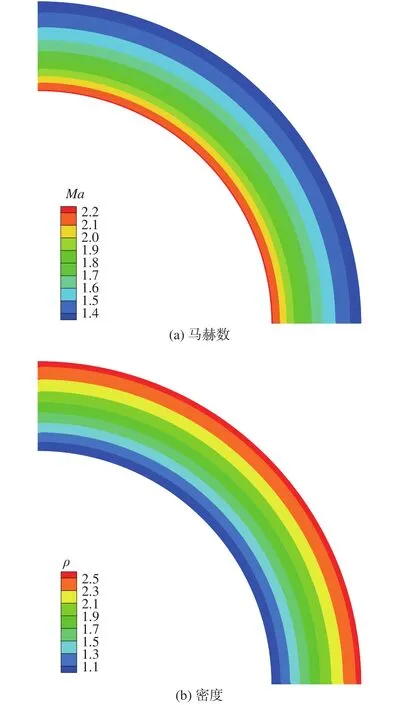
圖14 超聲速渦流場Fig.14 Flow fields of the supersonic vortex flow

同樣，分別測試了兩種不同長寬比網格下的計算結果，由于此算例包含曲線邊界，網格長寬比不像直線邊界網格在全場統一。因此采用壁面第一層網格的長寬比來近似代替。最疏一套網格示意圖，以及背景四邊形網格在徑向、周向的分布量如圖15與表4所示。該算例同樣測試了局部方向模板的計算效果，但與3.1節所反映出的計算結果一致，局部方向模板在該數值算例中出現計算發散的現象。因此，在統計誤差時只給出了共點、共面模板以及全局方向模板的計算結果。

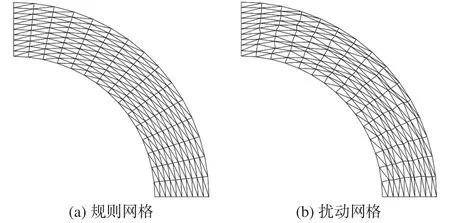
圖15 規則與擾動三角形網格Fig.15 Regular and randomly perturbed triangular grids

表4 不同長寬比下的背景四邊形網格在徑向與周向的分布量Table 4 The distribution of background quadrilateral grid cells in the radial and circumferential directions

為簡化結果分析，文中給出了長寬比AR≈ 4.0時的計算結果。圖16與圖17分別為在規則網格和擾動網格上，三種模板在全場以及壁面附近的誤差統計結果，表4中列舉的數據為規則密網格上的具體誤差值以及最后兩套網格間的計算精度。

從圖16中可以看出，不論在規則網格還是擾動網格上，三種模板得到的計算結果均接近求解器的設計精度。從誤差值來看，全局方向模板的L2誤差在三種模板中最低，L∞誤差與共面模板接近，并稍高于共面模板，但低于共點模板。在此基礎上統計了壁面附近的誤差值，其中最大誤差通常位于壁面，而L∞誤差曲線已在全場中統計，因此壁面附近只給出了L2誤差曲線。

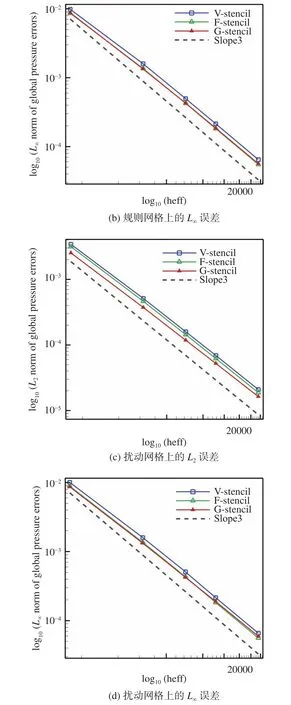
圖16 規則網格與擾動網格上的全場壓力誤差Fig.16 Global pressure errors on the regular and perturbed grids

從圖17可以看出，三種模板在壁面附近的誤差接近，但結合表5的數據可以看出，其中共面模板的誤差最低，全局方向模板的誤差與共點模板接近并稍低于共點模板。

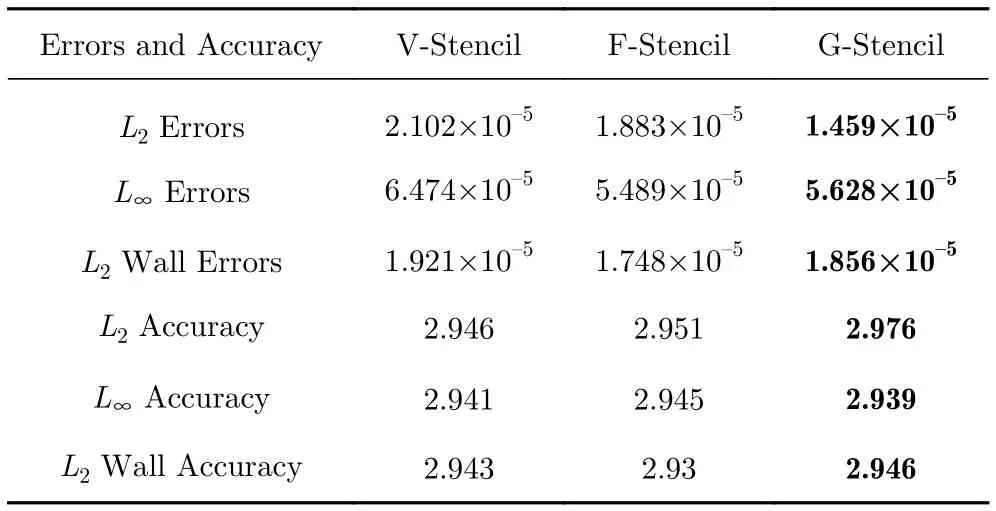
表5 規則密網格上的計算誤差以及最后兩套網格間的精度Table 5 Errors on the finest regular grid and computational accuracy between the last two sets of grids

圖17 規則網格與擾動網格上的壁面壓力誤差Fig.17 Wall pressure errors on the regular and perturbed grids

此外，從圖18可以明顯看出，全局方向模板所需要的模板單元數量更少，相比共點模板與共面模板，模板數量分別減少了57.9%與49.6%，在具備較高計算準確性的同時降低了重構過程的計算開銷。

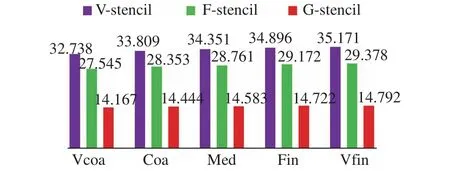
圖18 三種模板的平均模板單元數量Fig.18 Average stencil sizes of three different stencils

4 結 論

本文將全局方向模板推廣至高階精度非結構有限體積方法，并通過基于制造解的數值流動與真實超聲速渦流分別檢驗了全局方向模板在具有三階精度非結構有限體積求解器中的數值表現，得出以下結論：

1）首先從方法實現過程而言，全局方向模板選擇方法的過程簡便，相比局部方向模板，全局方向模板單元的確定有效避免了陣面推進與局部方向傳遞的繁瑣；相比常用的共點模板，新方法只需要在確定共點單元的的基礎上，找到與兩個全局方向相交的網格單元即可，該過程并未引入任何復雜性。

2）其次從計算結果來看，相比兩種常用的共點、共面模板，全局方向模板的使用可有效降低計算誤差，在測試的兩個數值算例中，全局方向模板均具有較好的數值表現。

3）此外，全局方向模板對不同長寬比的網格具有較強的適應性，擺脫了網格單元的拓撲約束，即使在大長寬比三角形網格上，模板單元始終能夠保證沿著壁面法向與流向，具有較好的空間延展性。

4）最后，基于全局方向的模板選擇方法從完全多維模板中提取了具有分維特征的模板單元，保證空間延展性的同時，可有效減少重構過程所需的模板單元數量。在具有三階精度的非結構有限體積求解器中，相比共點與共面模板，分別減少模板總數的57.9%與49.6%，可節約計算開銷。

綜上，全局方向模板在高階精度非結構有限體積方法中具有較好的數值表現，具備進一步推廣與應用的可行性。接下來的工作將從兩個方面分別開展：首先，從改善計算效率方面，針對計算域內的不同網格單元，進一步對比分析采用不同模板層數后幾種模板的計算效果，以控制重構過程所需要的模板單元數量；其次，從方法推廣與實際應用層面，應推廣該重構模板在二維、三維復雜外形以及粘性流動中的使用。同時，粘性項的高精度離散同樣也是下一步研究與關注的重點。