考慮飽和效應的無刷雙饋發電機功率模型預測控制

魏新遲 許利通 駱仁松 程 明 朱建國

（1. 國網上海市電力公司電力科學研究院 上海 200437 2. 東南大學電氣工程學院 南京 210096 3. 南瑞繼保電氣有限公司 南京 211102 4. 悉尼大學電氣與信息工程學院 悉尼 NSW 2006）

0 引言

無刷雙饋電機是一種近年來被重點關注的新型交流電機，其有兩個交流饋電端口和一個機械端口，通過定子勵磁的方式實現無刷化，可在保留普通雙饋系統優點的同時大大提高其可靠性，在大容量變速恒頻發電領域具有很好的應用前景[1-5]。但是無刷雙饋電機的結構和電磁關系較為復雜，導致相應的控制器設計難度較大，亟需對無刷雙饋電機的控制技術進行研究，以促進其發展及應用。

無刷雙饋電機矢量控制采用傳統的雙閉環結構，外環調節有功（或轉矩）和無功（或磁鏈），內環調節控制繞組電流的轉矩分量和磁鏈分量。但是這種控制方法將在靜態和動態性能間進行折中，從而達到相應的控制效果。直接功率控制（或直接轉矩控制）根據控制變量的調節誤差計算開關狀態來控制變流器，從而將調節誤差控制在合理范圍內，其控制結構簡單，魯棒性強，動態性能大大提高[10-15]。但該方法使用預設矢量表，無法準確控制功率（或轉矩），導致其出現較大脈動。后續有文獻研究模型預測控制，實現了功率的精確控制，具有優良的穩態與動態性能[16]。已有文獻對無刷雙饋電機的飽和建模與特性分析進行了廣泛研究。文獻[17-19]分別基于有限元法、等效磁路法和等效電路法建立了無刷雙饋電機的飽和模型，但是建模方法均較為復雜且并沒有進一步考慮控制性能的提升。文獻[20]在考慮飽和效應動態建模的基礎上設計了獨立運行控制器，實現了穩態與動態性能的雙提升。然而，現有的無刷雙饋電機并網運行控制方法均未考慮電機的飽和模型[6-12]。文獻[21-22]表明無刷雙饋電機的功率因數較低，飽和對電機參數的影響比傳統雙饋發電機更大，引起電機定子繞組電流和損耗增加，導致電機輸出轉矩/功率下降；考慮飽和效應后的計算值與實測值更加接近。因此，研究無刷雙饋電機高性能控制，需充分考慮電機飽和效應的影響。

本文提出考慮飽和效應的無刷雙饋發電機（Brushless Doubly-Fed Induction Generator, BDFIG）功率模型預測控制策略，在控制器中引入勵磁電感估算，明確了影響飽和效應的運行因素，實現了功率的精確控制，保證控制側電流的正弦度和較低的開關頻率。

1 BDFIG的建模與分析

1.1 BDFIG飽和效應模型

BDFIG在任意速坐標系下的動態數學模型可表示如下[23-24]。

電壓方程為

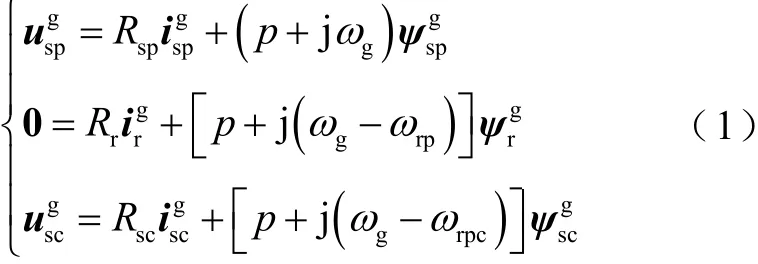
式中，上標g代表任意速坐標系；下標sp、r、sc分別代表功率繞組、轉子繞組、控制繞組；p為微分算子；R為電阻；u、i、ψ分別為電壓、電流、磁鏈矢量；ωg為任意速坐標系電角頻率；ωrp為功率側轉子繞組電角頻率；ωrpc為功率側與控制側轉子繞組相對角頻率。

磁鏈方程為

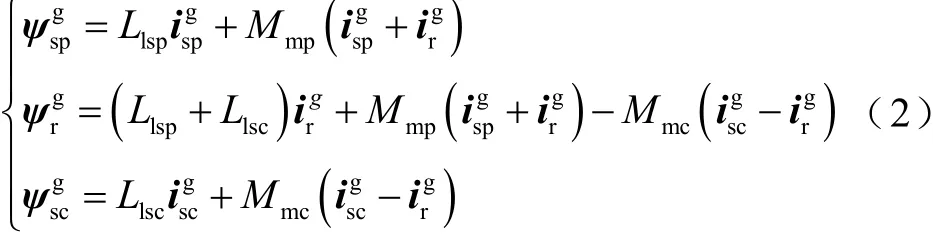
勵磁磁鏈方程為

其中

式中，Lsp、Llsp、Mmp分別為功率繞組自感、漏感和互感；Lsc、Llsc、Mmc分別為控制繞組自感、漏感和互感；Lr、Llr為轉子繞組自感和漏感。

將式（3）代入式（2），整理得到

式（4）表明，勵磁磁鏈可由各繞組磁鏈和電感值計算得到。考慮飽和效應的建模過程中，將勵磁電感作為輸入變量，每周期依據勵磁磁鏈的數值查表得到實時的電感值。綜上，考慮飽和效應的動態模型可表示如下。

電壓方程為

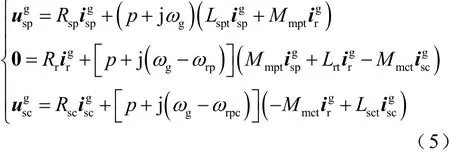
式中，Lspt=Llsp+Mmpt，Lrt=Llr+Mmpt+Mmct，Lsct=Llsc+Mmct。不考慮飽和效應時，Mmpt和Mmct為恒定值，勵磁磁鏈與勵磁電流之間呈線性化關系；考慮飽和效應時，Mmpt和Mmct為每周期依據飽和特性更新得到的數值，勵磁磁鏈與勵磁電流之間呈非線性關系。

轉矩方程為

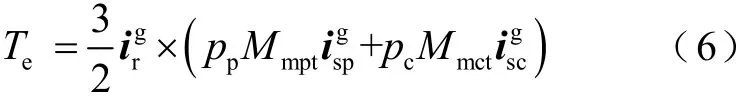
式中，pp和pc分別為功率繞組和控制繞組極對數。

1.2 穩態模型及功率分析

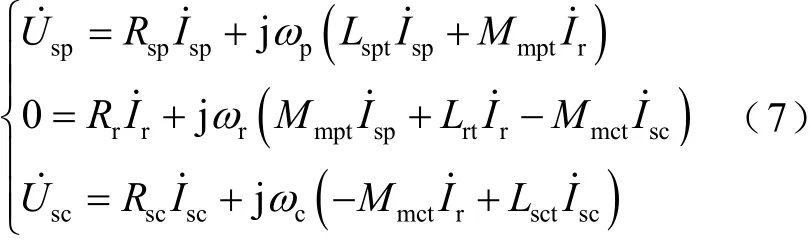
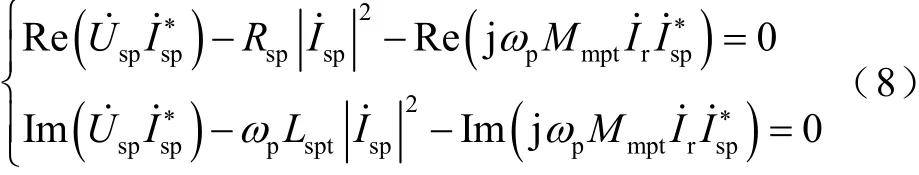
式（8）中第一個公式的三項分別為功率繞組有功功率、銅耗、氣隙有功功率；第二個公式的三項分別為功率繞組無功功率、電感消耗的無功功率、氣隙無功功率。式（7）中第三行方程兩邊同乘以并進行實部與虛部分解，可得

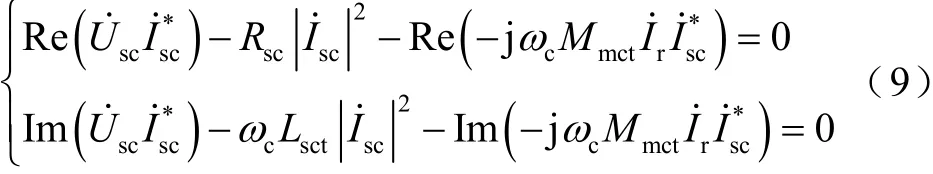
式（9）中第一個公式的三項分別為控制繞組有功功率、銅耗、氣隙有功功率；第二個公式的三項分別為控制繞組無功功率、電感消耗的無功功率、氣隙無功功率。

式中，第一個公式的三項分別為轉子銅耗、功率側與控制側氣隙有功功率、轉子機械功率；第二個公式的三項分別為轉子電感消耗的無功功率、功率側與控制側氣隙無功功率、轉子存儲的無功功率。

綜合式（8）~式（10），可得BDFIG的有功功率和無功功率分配如圖1所示。

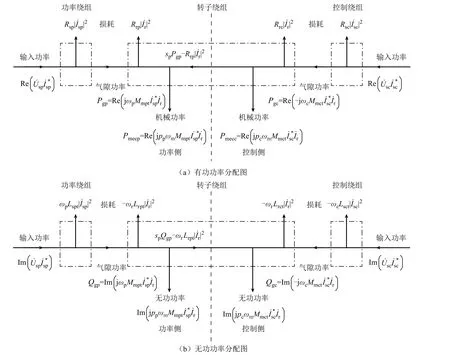
圖1 BDFIG功率分配圖Fig.1 Power distribution diagram of BDFIG

2 功率模型預測控制系統設計

2.1 功率預測模型

基于BDFIG考慮飽和效應的動態模型，可得狀態空間方程為[23]

其中

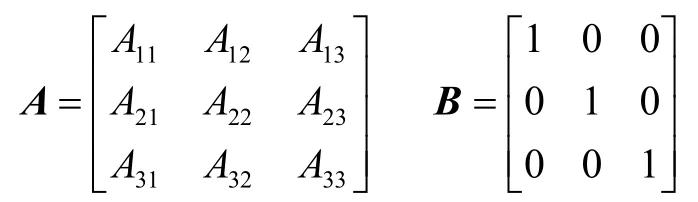
式中，X為狀態空間變量V為電壓矢量，矩陣A中A11~A33的表達式見附錄。

進一步推導得到功率繞組側的復功率矢量表達式為[23]

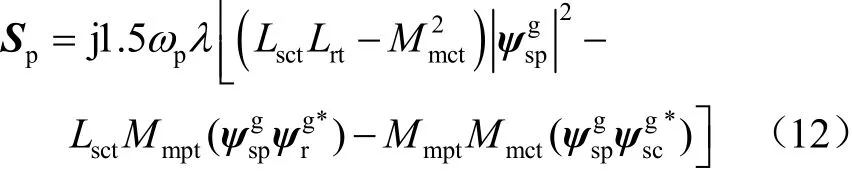
其中

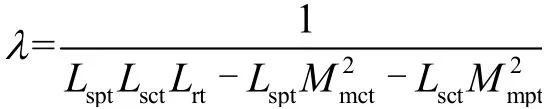
將復功率矢量對每個采樣周期進行求導并進行離散化處理，可得BDFIG的復功率預測模型為

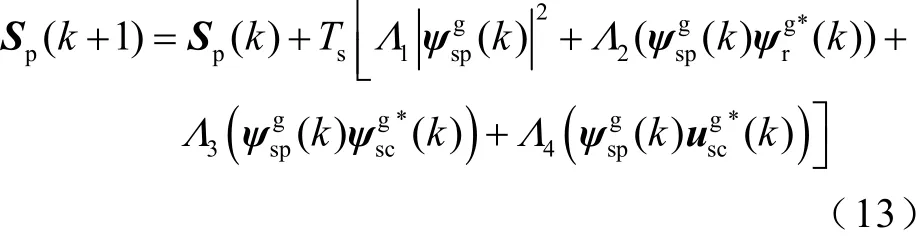
式中，sT為采樣周期，k∈N表示采樣時刻，Λ1~4Λ的表達式詳見附錄。

將式（13）分解，得到以有功功率和無功功率分別表示的預測模型為

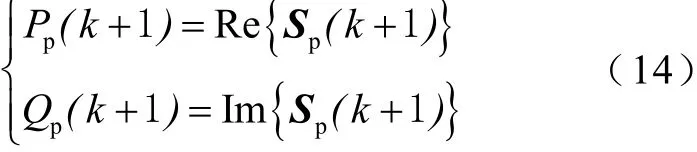
2.2 考慮飽和效應的功率模型預測控制系統

考慮飽和效應的功率模型預測控制系統框圖如圖2所示，主要包含勵磁電感估算、磁鏈估算、功率估算和預測、價值函數優化四個部分。

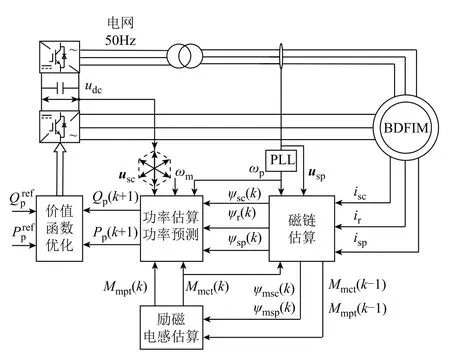
圖2 考慮飽和效應的功率模型預測控制系統框圖Fig.2 Block diagram of the model predictive power control system considering saturation effects

2.2.1 勵磁電感估算

本文以級聯式BDFIG為例，參數見表1。依據單饋空載實驗測點數據，采用多項式擬合得到功率側/控制側的勵磁電流imsp/c與勵磁磁鏈ψmsp/c關系如式（15）所示，飽和特性曲線如圖3所示。

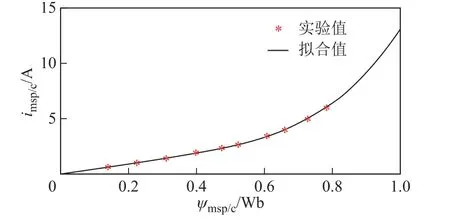
圖3 飽和特性曲線（功率/控制側）Fig.3 Saturation characteristic curve (power/control side)

表1 BDFIG參數Tab.1 Parameters of BDFIG

式中，a= 21.61,b= –18.32,c= 5.938,d= 3.912,e=0.002 437。

圖3 中，曲線的斜率對應勵磁電感Mmp/c的數值，可以看出當勵磁磁鏈大于0.6Wb時，電機逐漸進入飽和狀態，曲線出現拐點，斜率值（Mmp/c）變化明顯。因此，對于參數依賴性較強的功率模型預測控制，需要在每個周期對勵磁電感值進行估算，并作為控制器的輸入。

求解磁鏈方程式（4），可以得到第k周期功率繞組勵磁磁鏈和控制繞組勵磁磁鏈。考慮到一個周期中勵磁磁鏈基本保持不變，相應的勵磁電感改變較小，因此可基于第k-1周期的勵磁電感得到第k周期的勵磁磁鏈。仿真時，初始狀態值采用不飽和勵磁電感值。計算式為

基于圖3的擬合曲線，建立基于勵磁磁鏈（橫軸）-勵磁電流（縱軸）-勵磁電感（斜率）數值的lookup表格，通過勵磁磁鏈幅值查表可獲得每周期實時的勵磁電感值，即

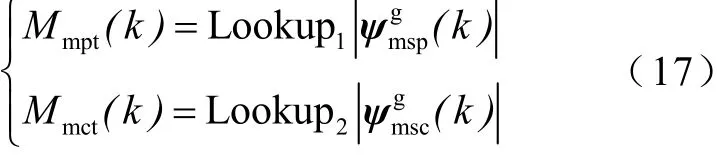
2.2.2 磁鏈估算模型

為了盡可能減少磁鏈估算模型對參數的依賴性并考慮飽和效應，采用磁鏈估算模型為

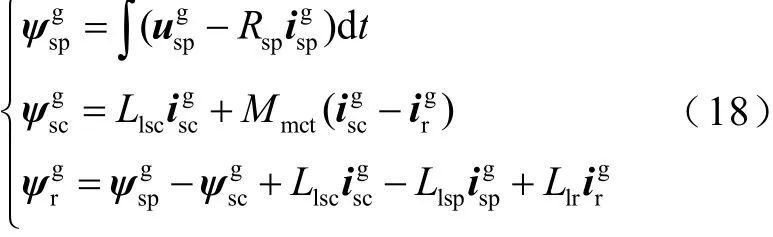
功率繞組磁鏈ψsp可通過usp?Rspisp的積分得到，并引入角度偏差與幅值偏差校正。磁鏈估算模型中引入控制繞組勵磁電感、漏感，功率繞組漏感、轉子繞組漏感。漏感數值較小且基本不受飽和效應的影響，可認為是恒定值，因此僅有控制繞組勵磁電感會影響磁鏈觀測的準確性。將考慮飽和效應的控制繞組勵磁電感Mmct作為磁鏈估算模型的輸入。

2.2.3 功率估算和功率預測

基于精確的磁鏈估算，可由式（12）估算功率繞組的功率，由式（13）計算得到功率預測模型。同樣，式中的漏感參數可視為恒定值，將考慮飽和效應的勵磁電感參數Mmpt和Mmct作為功率模型的輸入。

2.2.4 價值函數優化

為了達到期望的控制目標，設計滿足有功功率和無功功率控制目標及開關頻率限制的價值函數為

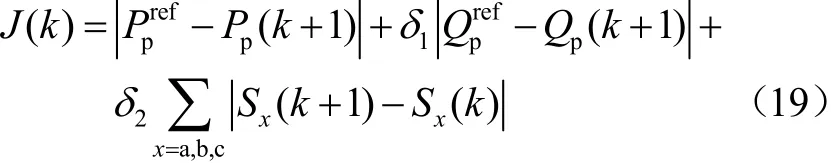
式中，Ppref和Qpref分別為有功和無功功率的參考值；Pp(k+1)和Qp(k+1)分別為有功和無功功率在k+1周期的預測值；Sx(k)和Sx(k+1)分別為k周期和k+1周期施加的開關狀態；δ1和δ2為權重系數。

式（19）中，第一項代表有功功率誤差最小化的控制目標；第二項代表無功功率誤差最小化的控制目標，將有功功率與無功功率控制分配相同的權重，系數δ1=1；第三項代表降低開關頻率的控制目標，在保證功率精確控制的前提下減小開關頻率，系數δ2=25。

3 仿真分析

基于Matlab/Simulink搭建仿真模型，采用多速率離散仿真的方法[25]，將控制器的仿真步長設置為100μs，實際物理系統的仿真步長為設置為2μs，BDFIG的主要參數詳見表1。

3.1 動態模型的仿真結果

BDFIG運行于650r/min，控制繞組連接電阻負載，控制繞組給定勵磁電壓幅值為98V，頻率為15Hz。圖4所示為動態模型的仿真結果。圖4中波形分別為功率繞組電壓usp、功率繞組電流isp、控制繞組電流isc、功率繞組勵磁磁鏈ψmsp、控制繞組勵磁磁鏈ψmsc和電磁轉矩Te，其中，虛線代表考慮飽和，實線代表不考慮飽和。由圖4中的結果可見，在動態建模中考慮飽和效應后，電壓、電流、磁鏈和轉矩脈動均明顯減小，控制繞組電流波形正弦度更好，勵磁磁鏈幅值保持在適當范圍。

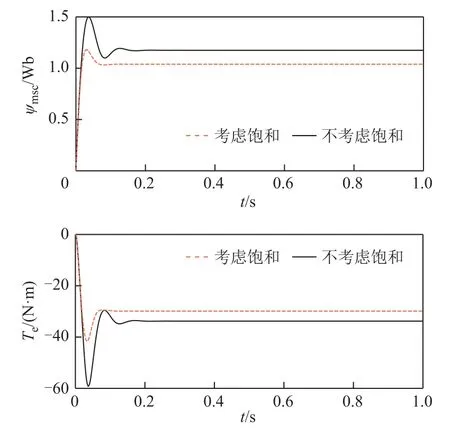
圖4 BDFIG動態模型仿真結果Fig.4 Simulation results of BDFIG dynamic model

3.2 功率模型預測控制系統的仿真結果

BDFIG并網運行時，功率繞組磁鏈較為恒定，為了簡化功率模型預測控制器的設計，僅考慮控制繞組勵磁磁鏈/電感的飽和效應。圖5a所示為考慮飽和與不考慮飽和的仿真對比（n=650r/min，Ppref=-600W，Qpref=0var），圖5a中波形分別為功率繞組電流isp、控制繞組電流isc、控制繞組勵磁磁鏈ψmsc和勵磁電感Mmc。可以看出考慮飽和時，控制繞組側的勵磁磁鏈、勵磁電感及電流的數值與不考慮飽和時相差較大。其中，控制繞組勵磁電感值約為184.5mH，而不飽和電感值為220mH，表明此時的飽和效應較為明顯。表2所示為不同轉速下的飽和電感數值，隨著轉速的上升，飽和電感值逐漸偏離不飽和值，飽和效應的影響增加。圖5b所示為無功適量（Qpref=500var）與無功為零（Qpref=0var）的仿真對比（n=650r/min，Ppref=-600W）。給定無功的情況下，功率繞組電流幅值變大，控制繞組電流幅值與勵磁磁鏈幅值變小，勵磁電感數值與不飽和電感數值較為接近，此時飽和效應的影響較小。因此，在實際運行中，為了減小飽和效應的影響并保證控制效果，需向BDFIG提供適當的無功功率并使其運行在較低轉速。上述結果進一步表明，飽和效應對勵磁電感數值和勵磁磁鏈水平影響較大。可以預見，當實際電機運行于較為飽和的狀態時，若控制器中的勵磁參數仍采用不飽和電感值，將會與電機實際狀態時的參數偏差較大，最終導致功率控制出現偏差，電流波形受到影響。

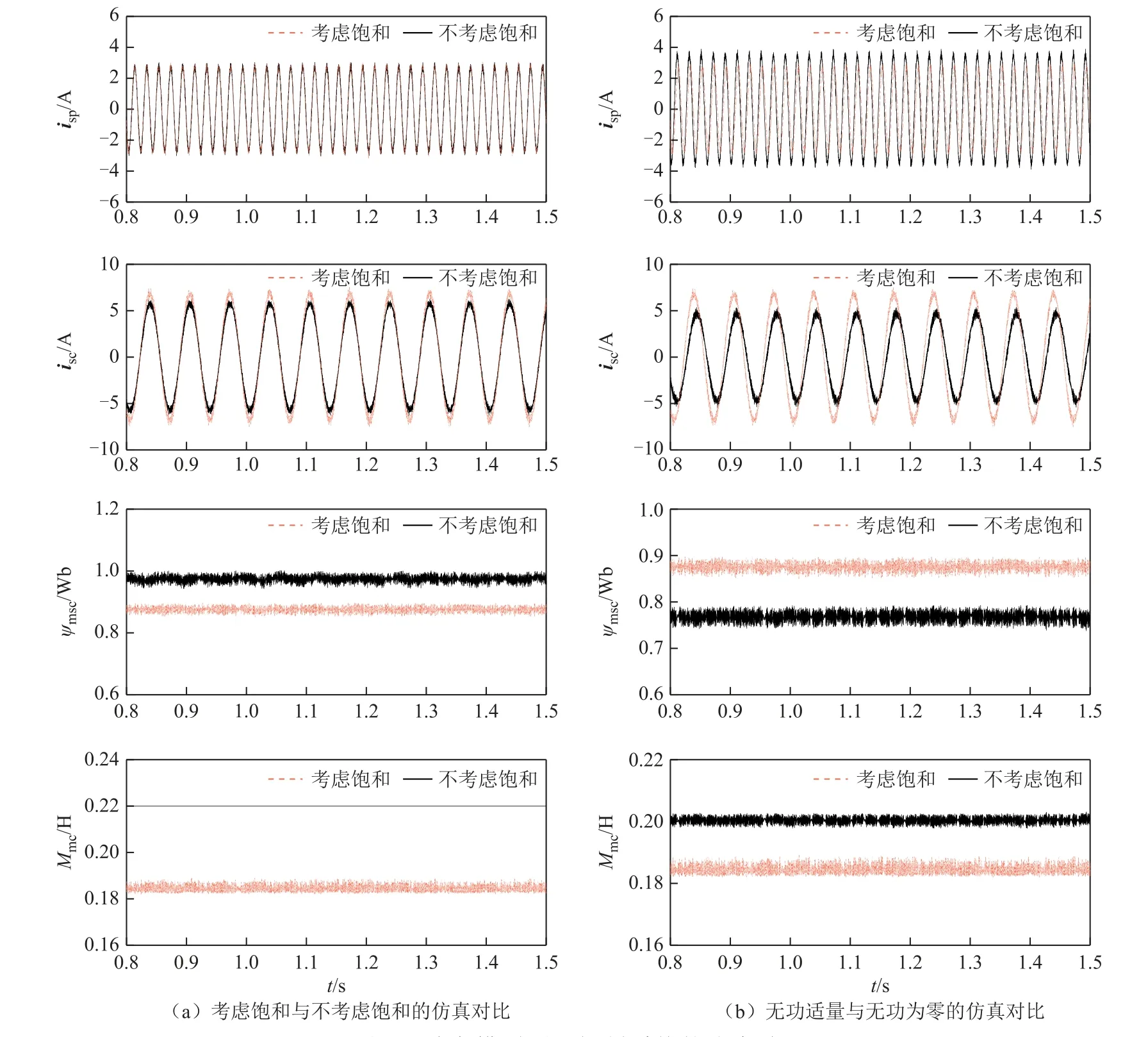
圖5 功率模型預測控制系統的仿真結果Fig.5 Simulation results of the power model predictive control system

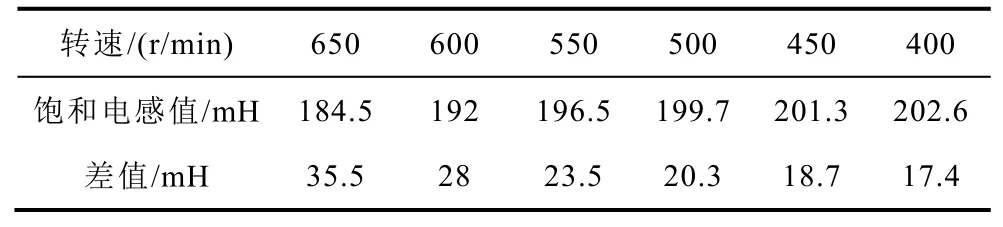
表2 控制繞組勵磁電感值Tab.2 Magnetic inductance of control wires

4 實驗分析

為了測試考慮飽和效應的功率模型預測控制系統的實際效果，使用圖6所示的實驗平臺進行驗證，包括原動機、級聯式BDFIG、逆變器、dSAPCE系統等。依據仿真得到的結論，在實驗中考慮400~600r/min的運行范圍，給定Qp=500var的無功功率，每周期估算勵磁電感值作為功率模型預測控制器的輸入，盡可能減少飽和效應產生的影響。

圖6 無刷雙饋發電系統實驗平臺Fig.6 Experimental platform of brushless doubly-fed system

圖7 所示為穩態運行的實驗結果，BDFIG運行在400r/min，有功功率參考值為-600W，無功功率參考值為500var，圖中波形分別為有功功率Pp、無功功率Qp、功率繞組電流isp、控制繞組電流isc和開關頻率n。從實驗結果可以看出，有功和無功功率均能很好地跟蹤參考值，控制繞組電流較為正弦，開關頻率約為1.3kHz。圖8所示為變速運行的實驗結果，電機轉速從400 r/min逐漸上升至600 r/min，有功功率參考值為-600W，無功功率參考值為500var。從實驗結果可以看出，控制繞組電流頻率隨著轉速發生變化，而功率繞組頻率保持不變，實現了BDFIG的變速恒頻運行。圖9所示為變速運行且有功功率參考值階躍變化情況下的結果，電機轉速從450r/min逐漸上升至550r/min，有功功率參考值從-400W階躍至-600W，再從-600W階躍至-500W，無功功率參考值為500var。從實驗結果可以看出，有功功率能夠很好地跟蹤階躍給定信號，且無功功率不受影響，說明有功功率和無功功率可實現很好的解耦控制。上述實驗結果驗證了本文所提控制系統的有效性。

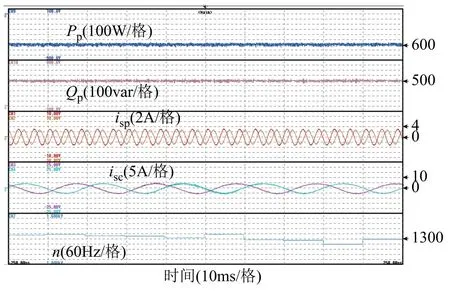
圖7 穩態運行時的實驗結果Fig.7 Experimental results under steady-state operation

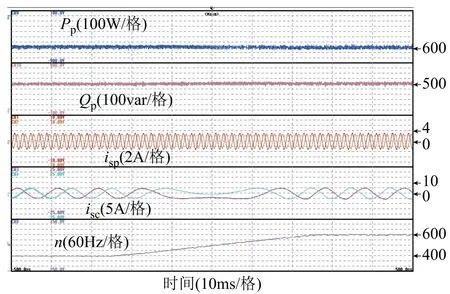
圖8 變速運行時的實驗結果Fig.8 Experimental results under various speed operation

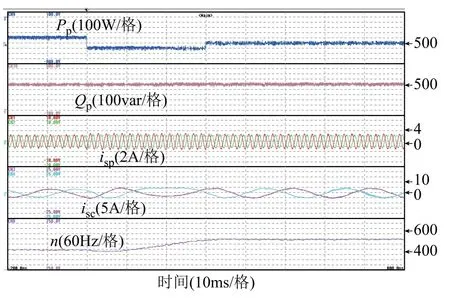
圖9 變速運行且有功功率給定階躍變化時的實驗結果Fig.9 Experimental results under various speed and active power condition

5 結論

本文針對BDFIG，建立了任意速坐標系下考慮飽和效應的動態模型，詳細分析了有功功率與無功功率分配，提出了考慮飽和效應的功率模型預測控制策略。為驗證飽和模型及本文所提功率模型預測控制策略的有效性，對BDFIG系統進行建模，并搭建了相應的實驗平臺。實驗結果表明，在動態建模中考慮飽和效應后，電壓、電流、磁鏈和轉矩脈動均明顯減小，控制繞組電流波形正弦度更好，勵磁磁鏈幅值保持在適當范圍。向BDFIG提供適當的無功功率并使其運行在較低轉速，可有效減小飽和效應的影響并保證控制效果。本文所提考慮飽和效應的功率模型預測控制具有快速的動態響應，能夠實現有功功率和無功功率的精確控制及解耦控制，保證控制側電流正弦度和較低開關頻率。

附 錄

式（11）矩陣A中A11~A33的表達式為