火焰穩定器修形對發動機后向RCS 的影響

姚倫標，杜 凱，李 寧，張 琪，于明飛

（中國航發貴陽發動機設計研究所，貴陽 550081）

現代戰爭中，飛行器的低可探測性能已成為其戰場生存能力的一項重要技術指標。飛行器的低可探測性可分為雷達隱身、紅外隱身、光學隱身和聲學隱身等多學科方向。根據目前戰時環境的主要探測手段，飛行器的隱身能力主要指雷達隱身和紅外隱身，而發動機的后向低可探測性能將直接影響著飛機的后向隱身性能[1?2]。要實現發動機的后向雷達隱身，直接手段是控制和降低發動機自身的后 向 雷 達 散 射 截 面（Radar cross section，RCS）大小。

發動機的后向RCS 構成主要是由低壓渦輪、加力燃燒室及可調噴管等部件組成的排氣腔體RCS，其具有腔體散射機理復雜、散射強度高和寬角域等特征，是飛機后向的主要雷達散射貢獻源之一。火焰穩定器是航空渦輪發動機加力燃燒室的基本結構之一，是實現加力點火及穩定燃燒的關鍵功能部件，但其位于加力燃燒室的某一橫截面上，雷達波照射后可形成直接鏡面反射或與壁面多次反射及繞射等相互作用后形成強回波散射，通過簡化模擬測試得出對其采用隱身措施后在高頻下對腔體RCS 縮減高達60%左右。對于非隱身設計發動機，穩定可靠工作是其設計的重要出發點，但對于具有隱身需求的航空發動機，基于穩定、可靠工作結構的隱身改進設計也是其重要研究方向。

本文基于某型蒸發式穩定器結構，在不改變穩定器主體結構的前提下，從隱身修形設計角度改進設計穩定器蒸發腔局部結構及傾斜布置，一方面使結構修形具有一定的RCS 縮減效果；另一方面改善功能材料的使用工況，以提高發動機的后向雷達隱身能力。

1 穩定器對發動機后向RCS 貢獻分析

為了評估穩定器對發動機后向腔體RCS 的貢獻大小，開展了簡化排氣腔體的靜態RCS 測試。狀態1 為穩定器蒸發腔金屬狀態，狀態2 為穩定器蒸發腔采用高頻（8～18 GHz）具有較好吸波性能的吸波材料（低頻性能較差）遮擋，目標的其他結構一致。分別對目標0°俯仰在L、S、C、X 及Ku 波段幾個核心頻點的水平極化（Horizontal to horizon?tal，HH）及垂直極化（Vertical to vertical，VV）開展RCS 測試，其在±45°統計角域均值縮減對比如表1 所示。

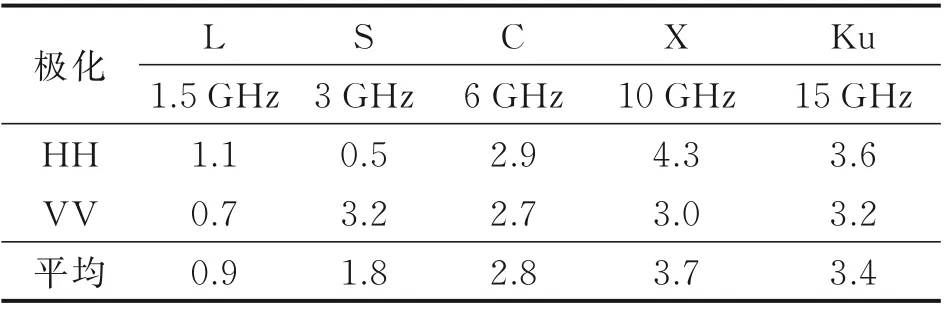
表1 狀態2 較狀態1 的縮減效果Table 1 Reduction of State 2 compared with State 1

從表1 中可知，低頻L、S 波段狀態2 較狀態1在統計角域內的均值縮減量均較小，最高縮減1.8 dB，最小縮減僅0.9 dB，這與用于遮擋穩定器蒸發腔的吸波材料在低頻下吸收性能差有關系。在C 波段統計角域的均值縮減約3 dB。在高頻X、Ku 波段，狀態2 較狀態1 在各偏航角域內的均值縮減量均較大，X 波段HH 極化下的最大縮減達4.3 dB（按百分比縮減為62.8%），統計角域極化均值的平均縮減約3.5 dB。此外，通過其他統計角域均值變化分析可得，隨著均值取值角域的增大，其均值縮減幅度變小，這是因為腔體散射在正后向0°附近為主散射峰，隨著偏航角的增大峰值減小。

可以得出，高頻下在穩定器蒸發腔采用吸波材料涂覆對發動機排氣腔體的后向RCS 縮減效果顯著，對于非隱身一體化設計的航空發動機加力燃燒室，采取相應措施（如隱身涂層、修形設計等）降低穩定器對排氣腔體RCS 的貢獻將直接縮減發動機后向RCS 大小。

2 電磁計算方法

2.1 迭代物理光學法

針對航空發動機排氣系統這類電大尺寸復雜腔體目標的電磁散射求解問題，其計算規模之大是目前低頻數值算法難以解決的瓶頸，采用高頻近似算法是在兼顧效率與精度的相對有效辦法之一[3]。迭代物理光學法（Iterative physical optics, IPO）是一種建立在物理光學法（Physical optics, PO）基礎上的高頻計算方法，考慮腔體壁面對電磁波的多次反射，通過迭代方法求解電場積分方程，再求解計算得到腔體的散射場[4?6]。

假定入射電磁波為平面波，對于如圖1 所示的理想導體材料腔體結構，其腔體內壁面Sc上的初始電流J0(rc)可以由物理光學法直接近似得出

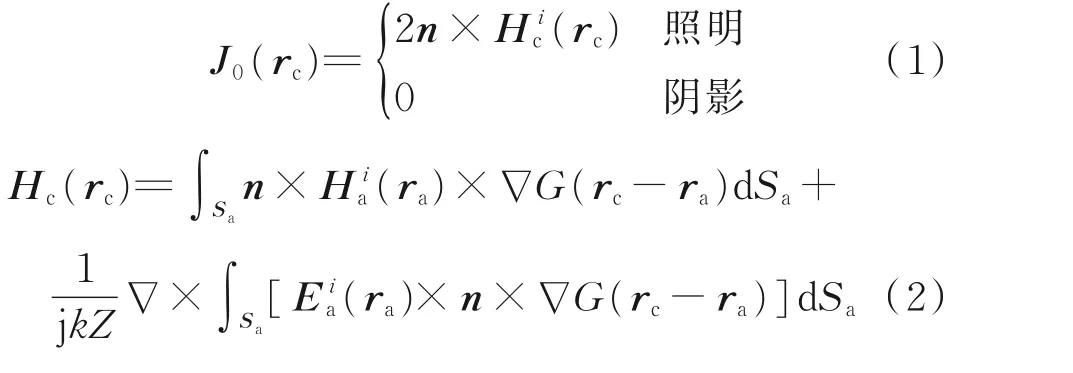
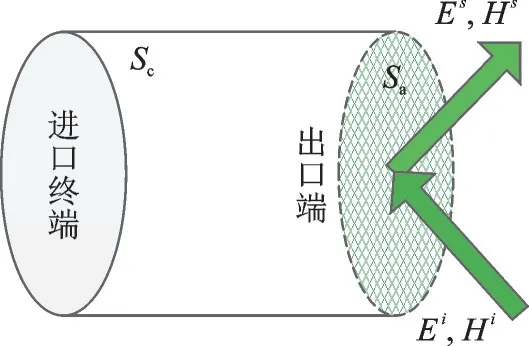
圖1 腔體結構示意圖Fig.1 Schematic diagram of the cavity

式中：下標n表示迭代次數；P.V.∫Sc為 在腔體內壁面Sc區域內主值積分，考慮各個面元之間的遮擋關系[8]，即可模擬計算出腔內壁Sc上電磁波在的多次反射效應。通過式（2）得到內壁面Sc上的感應電流J(rc)，結合遮擋關系判斷，由Kirchhoff 公式可得口徑面Sa上的散射場，利用電磁場等效原理及遠場條件，即可得到腔體的遠場某點處的散射電場Es[3,9]。

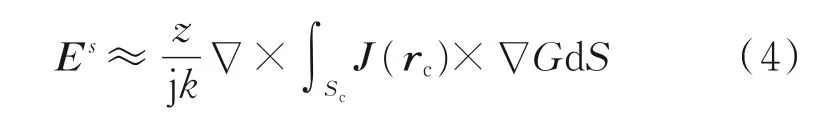
式中：?用（-jω）代替，其中ω為自由空間波矢，便可得到散射電場Es在球面坐標系中的相應的各個分量[10]。再根據雷達雷達散射截面的定義，即可得到目標RCS 的近似結果，即有

相比于其他高頻方法，IPO 能夠有效解決電大尺寸腔體散射問題，每平方波長網格剖分9～16 個面元即可達到精度要求，不需要矩陣求逆，內存消耗少，同時為了提高IPO 方法的迭代計算效率，在迭代過程中采用前后向物理光學法迭代方法[11?12]和松弛因子技術[13?14]。根據經驗，一般不太復雜的腔體取0.8～0.9，較復雜的腔體取0.6～0.7[13]。本文計算中的松弛因子為0.65。

在噴管的雷達散射特性計算過程中，噴管壁面采用三角面網格的大小與計算的電磁波入射波長相關。為了滿足迭代物理光學法計算精度需求，每波長平方等于9～16 面元這一條件，其網格邊長計算公式為

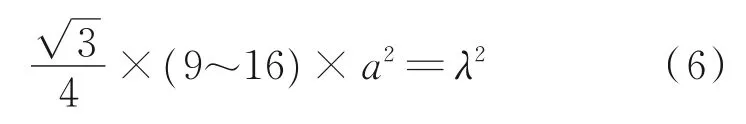
式中：λ為入射波的波長；c為光速；f為入射波的頻率；a為網格邊長。同時，由于IPO 與腔體內部網格無關，為了提高計算效率，可以在腔體內部生成較粗的內部連通體網格，提高其計算效率。

2.2 仿真算法驗證

本文IPO 算法程序是基于西工大動力與能源學院研究成果，為了驗證IPO 方法的正確性，以文獻[15]的單端開口的軸對稱腔體（圖2）為驗證模型，其長度、直徑都為4λ（λ為波長），計算頻點為10 GHz。

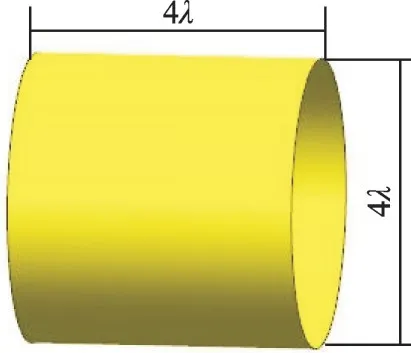
圖2 驗證計算模型Fig.2 Validated calculation model

利用IPO 程序仿真計算結果與文獻[15]中的試驗結果對比，結果如圖3 所示，可見本文的IPO 算法結果與文獻數據吻合良好，表明其計算結果可靠。

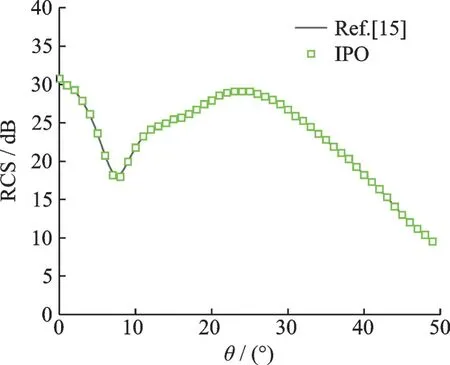
圖3 腔體散射驗證計算結果對比Fig.3 Comparison of calculation results of scattering filed of cavity

此外，在文獻[16]中，對1/2 縮比的軸對稱排氣系統開展了室內暗室RCS 測試與采用IPO 仿真計算結果的對比分析，結果表明在±50°角域內仿真均值結果與測試結果的相對誤差在10.6%內，故本文采用IPO 方法用于類似復雜程度的腔體RCS研究具有一定的精確性和可靠性。

3 穩定器蒸發腔結構修形的RCS 對比分析

3.1 不同穩定器蒸發腔結構修形簡化模型

基于穩定器在傳統加力燃燒室構成的發動機后向RCS 中為主要強散射貢獻源之一，通過對現有某型蒸發式穩定器結構及特征進行分析，在不改變穩定器整體結構及布置情況下，將火焰穩定器簡化為由12 個徑向穩定器環形布置。按照通過對蒸發腔局部結構修形將入射電磁波偏置到非后向可直接探測方向的設計原則，設計了4 種不同的穩定器蒸發腔改進結構（如圖4 所示，蒸發孔均未示出）。其中，WDQ1 為原結構，WDQ2 為平板結構，WDQ3 為內凹結構，WDQ4 為外凸結構，WDQ5 為縱向和橫向復合傾斜的平板結構。模型的縱向長度為300 mm，橫截面最大寬度為30 mm。

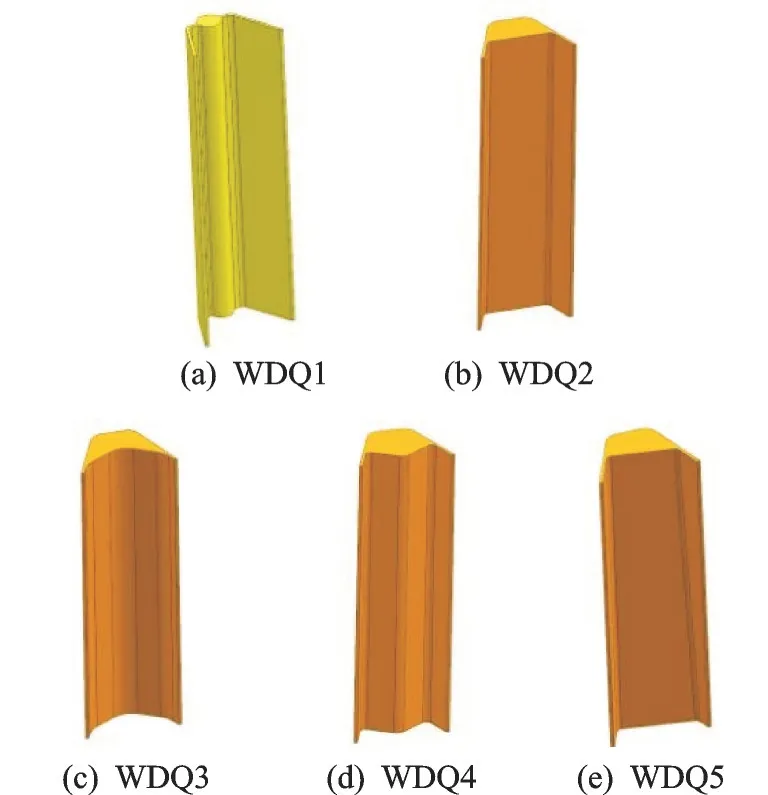
圖4 不同穩定器蒸發腔結構修形簡化模型Fig.4 Flame stabilizer with different evaporation chamber simplified models

3.2 計算模型

發動機的排氣腔體的簡化結構示意如圖5所示。其真實結構十分復雜，含很多小零件、間隙、臺階及孔等散射源，通過目前的電磁仿真計算方法很難實現精確數值模擬分析。本文將發動機排氣腔前端低壓渦輪葉片截面用短路終端簡化模擬，相關研究顯示短路終端與葉片終端的電磁散射結果誤差在可接受的范圍內[17?18]，加力筒體、隔熱屏及可調噴管等構成的復雜腔體壁面結構簡化為圓柱體管道腔體（長度800 mm，直徑600 mm），由于內錐體的軸向投影面積較大且可形成腔體內的多次反射，故計算模型保留內錐體結構形式，忽略噴油桿等其他結構的影響，針對不同的穩定器蒸發腔結構形式的RCS 縮減對比分析。簡化的計算模型如圖6所示。

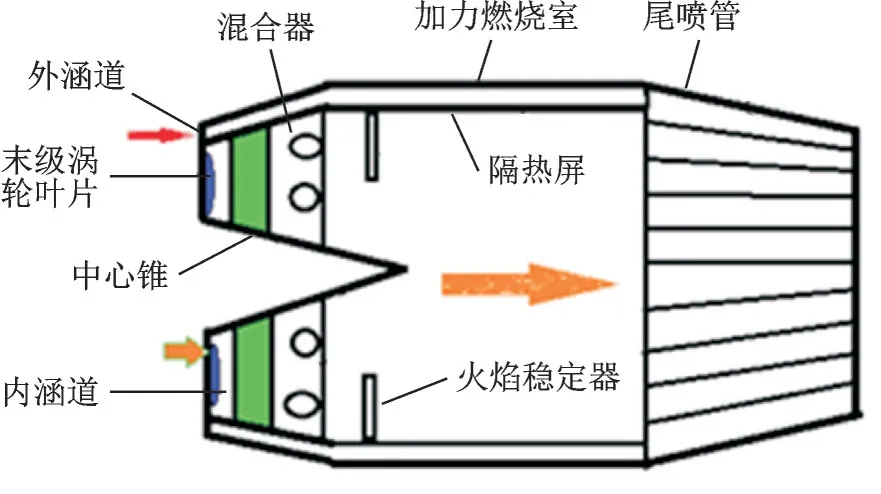
圖5 發動機排氣腔體結構示意圖Fig.5 Schematic diagram of engine exhaust cavity structure

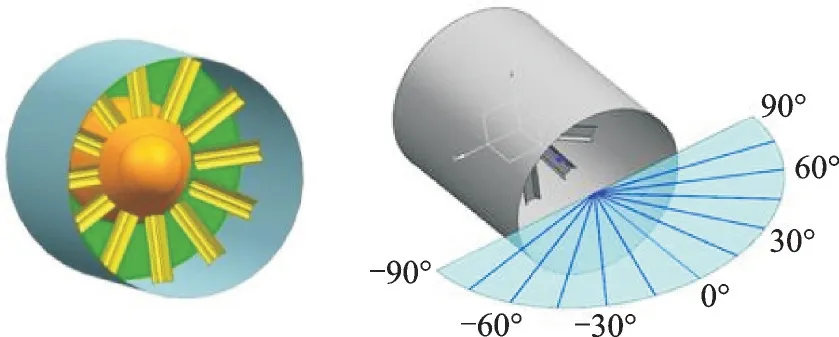
圖6 簡化的腔體計算模型Fig.6 Simplified calculation cavity model

根據當前軍用體制探測雷達的常規威脅波段主要在L、S、C、X、Ku 等，綜合計算資源分別選擇1.5 GHz（L 波段）、10 GHz（X 波段）作為低頻及高頻的計算頻點。設定雷達探測平面為xoy，x軸正方向入射的探測方位角θ為0°，計算時θ取0°～45°，間隔為1°。采用單站雷達系統進行模擬，分別計算得到在HH、VV 不同極化方式下，不同結構在不同波段典型頻點下的點頻RCS 對比曲線。

3.3 計算結果分析

3.3.1 點頻RCS 曲線分布特征

高頻10 GHz 時不同極化的RCS 曲線分布分別如圖7、8 所示，低頻1.5 GHz 時不同極化的RCS曲線分布分別如圖9、10 所示。

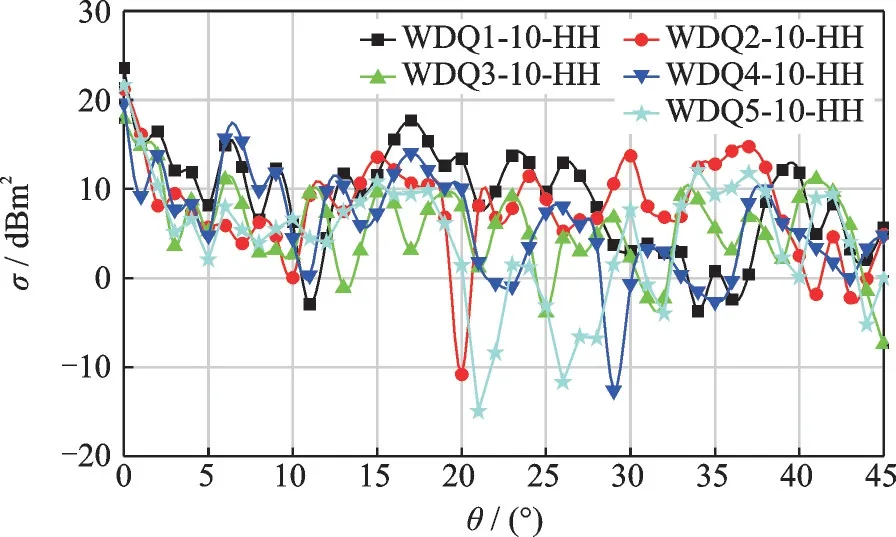
圖7 10 GHz 時水平極化下RCS 曲線Fig.7 RCS curves of HH at 10 GHz

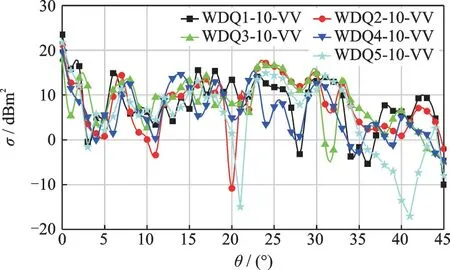
圖8 10 GHz 時垂直極化下RCS 曲線Fig.8 RCS curves of VV at 10 GHz

圖9 1.5 GHz 時水平極化下RCS 曲線Fig.9 RCS curves of HH at 1.5 GHz

從圖7、8 可看出，在高頻時、兩種極化方式下，5 種不同結構的RCS 在方位角θ=0°即正后向入射時最大，此時入射電磁波直接照射腔體內各部件的截面積最大，電磁散射回波直接反射出腔體出口被探測到，形成強回波。隨著方位角θ在[0°，20°]內增大，不同極化下的RCS 曲線總體特征具有趨同的變化趨勢，但不同結構的RCS 大小不一。可以看到在θ=6°及θ=17°附近，各種不同結構的穩定器構成的腔體RCS 均存在一個較大峰值；在θ=20°附近均存在一個下降的峰值；隨著θ進一步增大，各種結構的RCS 在一定范圍內振蕩分布。WDQ5由于其具有復合角的結構特征，電磁波照射時發生了偏轉，使在多數入射角下后向能接收到的回波強度較其他幾種結構要低。

從圖9、10 中可見，低頻下，各種穩定器蒸發腔結構構成的腔體RCS 變化趨勢基本一致，這是由于低頻下電磁波的波長較長，對于這種較小尺寸的結構變化不敏感產生的。在HH 極化下，在方位角[10°，25°]時，蒸發管式（WDQ1）穩定器構成的腔體RCS 相對較小；隨著方位角的增大在[30°，45°]時，改進的幾種穩定器蒸發腔結構構成的腔體RCS 相對于WDQ1 都要低。總體來看，具有復合角度平板傾斜的WDQ5 構成的腔體RCS 在大多數方位角下都具有一定優勢。

3.3.2 RCS 均值特征

高頻10 GHz 時不同極化、不同統計角域的RCS 均值分別見表2、3；低頻1.5 GHz 時不同極化、不同統計角域的RCS 均值分別見表4、5。下文所述RCS 統計均值均采用無量綱化（各角域均值/各角域均值中最大值）處理，不再贅述。

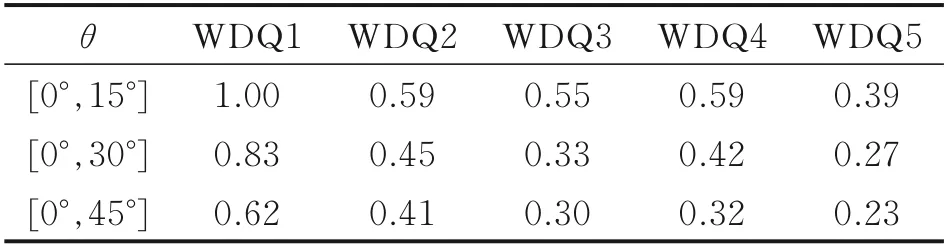
表2 10 GHz 時水平極化下RCS 均值Table 2 Average values of RCS at HH of 10 GHz

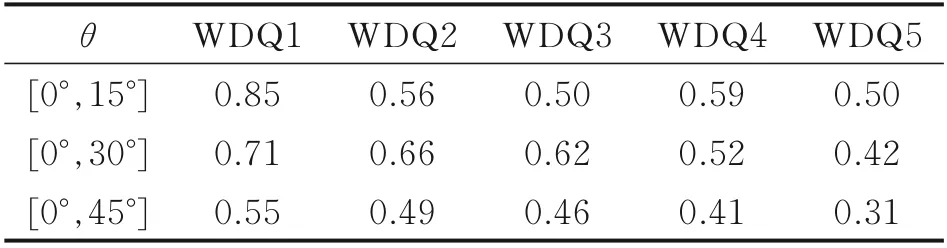
表3 10 GHz 時垂直極化下RCS 均值Table 3 Average values of RCS at VV of 10 GHz

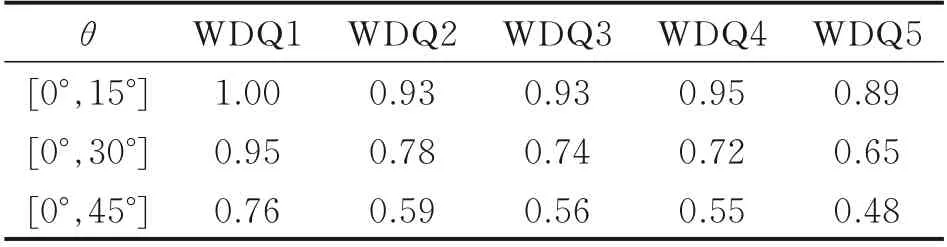
表4 1.5 GHz 時水平極化下RCS 均值Table 4 Average values of RCS at HH of 1.5 GHz

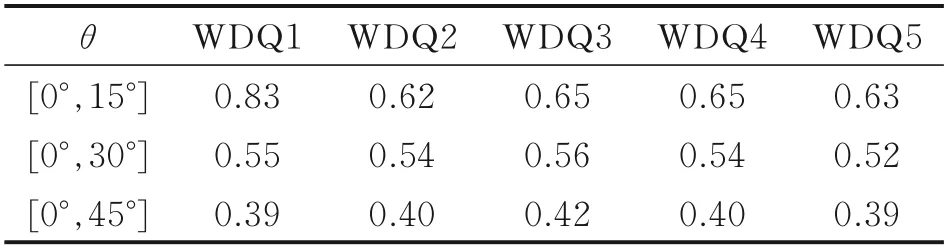
表5 1.5 GHz 時垂直極化下RCS 均值Table 5 Average values of RCS at VV of 1.5 GHz

從表2、3 可見，5 種不同蒸發腔結構的穩定器構成的腔體RCS，統計角域[0°,15°]的均值在不同極化下基本一致，表明電磁波小角度入射時目標腔體中細微結構變化的RCS 結果對極化方式不敏感；隨著統計角域的增大，每種結構的RCS 均值在垂直極化下較水平極化都要略大。帶復合角傾斜的平板結構WDQ5 構成的腔體RCS 較其他結構在各統計角域的均值相對較小，在[0°,45°]角域，2 種極化的均值平均縮減約50%。

從表4、5 可見，不同穩定器蒸發腔結構構成的腔體RCS 在各探測角域內的均值相差很小，但垂直極化下相比較水平極化下的結果小，WDQ1 相差最大約50%。與高頻下的統計結果相比，低頻下的極化差異帶來的結果差異比高頻大，結合圖10 的RCS 曲線特征，在垂直極化下，當θ角大于30°后存在一個較低極值，不同極化下腔體內發生多次反射后逃逸出等效口徑面上被接收的電磁回波強度減弱。帶復合角傾斜的平板結構WDQ5 蒸發腔穩定器構成的腔體RCS 較其他結構在[0°,45°]角域，2 種極化的均值平均縮減約24%。

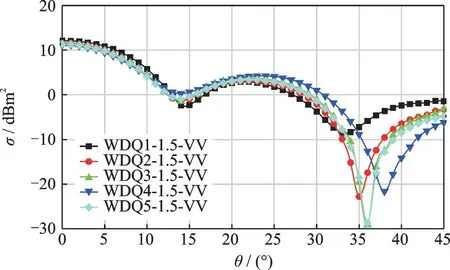
圖10 1.5 GHz 時垂直極化下RCS 曲線Fig.10 RCS curves of VV at 1.5 GHz

4 穩定器傾斜布置的RCS 對比分析

4.1 穩定器傾斜布置簡化計算模型

傳統的火焰穩定器垂直于加力燃燒室軸線的某一平面上周向均勻分布，不利于發動機的后向隱身設計。為了進一步對比研究穩定器傾斜布置對腔體RCS 的影響，基于WDQ2 平板結構蒸發腔，穩定器頂端位置固定，穩定器根部向加力燃燒室進口端、噴管出口端各傾斜10°、20°和30°，設定向加力燃燒室進口端傾斜為負，向噴管出口端傾斜為正，其對比計算分析如圖11 所示的不同傾斜角度腔體RCS 特征，其中腔體結構及計算角域同3.2 節所述。

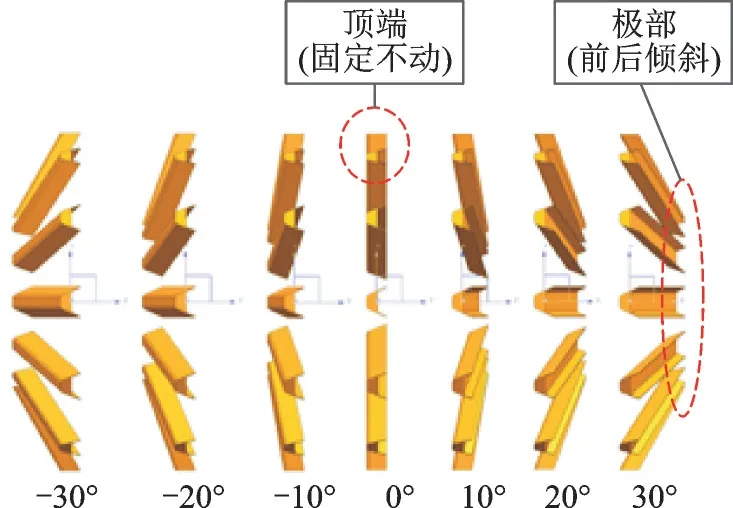
圖11 穩定器角度傾斜方案Fig.11 Scheme of stabilizer angle tilt

4.2 計算結果分析

4.2.1 點頻RCS 曲線分布特征

綜合考慮計算效率與計算精度，選擇入射頻率為9.4 GHz 研究其雷達散射特性。9.4 GHz 時不同極化的RCS 曲線分布分別如圖12、13 所示。

圖12 水平極化不同傾斜角度下腔體RCS 曲線分布Fig.12 Distribution of cavity RCS curves at different tilt an?gles under horizontal polarization

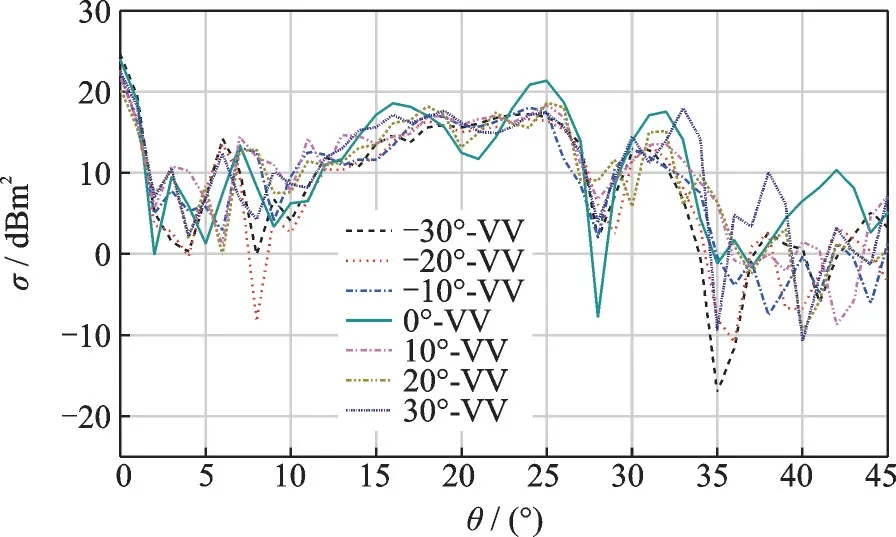
圖13 垂直極化不同傾斜角度下腔體RCS 曲線分布Fig.13 Distribution of cavity RCS curves at different tilt an?gles under vertical polarization

圖12、13 所示為水平、垂直極化下穩定器不同傾斜角度時腔體RCS 隨探測角的變化分布曲線。從圖中可以看出，不同傾斜角狀態下的RCS 角向分布規律相似，在0°探測角附近6 種不同傾斜角度狀態下的腔體RCS 都達到最大值，這主要是因為在0°探測角附近時，由于噴管進口處進行了終端封閉，平面的直接反射起主要貢獻，使得噴管軸線附近會產生很強的鏡面反射，導致這個方向上的RCS 值較高。隨著探測角度的增加，各狀態下的RCS 值呈下降趨勢，并逐漸出現波峰波谷。從水平極化方式下的RCS 角向分布曲線可以看到，穩定器傾斜狀態下的RCS 分布曲線在波峰波谷位置較未傾斜狀態有一定角度差，而垂直極化下差距不大，說明在水平極化下腔體RCS 變化對穩定器傾斜較為敏感。

4.2.2 RCS 均值特征

表6、7 為偏航探測面水平、垂直極化下各探測角域內的RCS 平均值。RCS 均值進一步降低，且穩定器傾斜20°狀態RCS縮減得更加明顯，最大縮減了約38%；在其余探測角域下的均值縮減不明顯。這表明在水平極化下穩定器傾斜-20°～20°范圍內，在大探測角域下對腔體RCS 均值影響不大。隨著傾斜角度增大到-30°～30°時，各探測角域下的均值呈上升趨勢，且傾斜-30°狀態下的均值上升幅度更大。

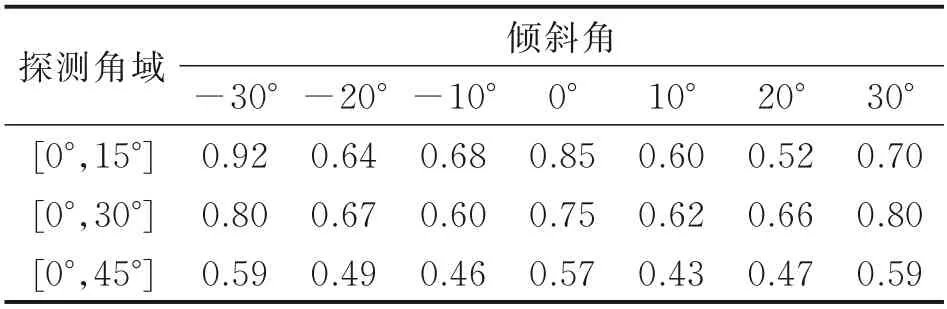
表6 水平極化下各探測角域的無量綱RCS 平均值Table 6 Dimensionless RCS average values of each de?tection angle under horizontal polarization

表7 中垂直極化下在0°～15°探測角域時，穩定器傾斜20°狀態時的RCS 縮減較為明顯，相較未傾斜狀態縮減了約39%，隨著探測角度的增大，可以看到穩定器傾斜-20°～20°狀態下的均值相差不大。當傾斜角度增大到-30°，在0°～15°探測角域下的均值呈上升趨勢，增大了約2%；當傾斜角度增大到30°，各探測角域下的均值縮減效果減小。綜合可得，穩定器向下游傾斜在0°～20°對腔體RCS 具有更好地縮減效果。

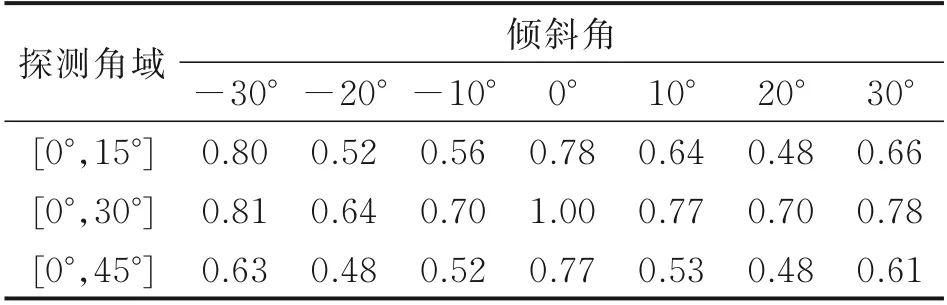
表7 垂直極化下各探測角域的無量綱RCS 平均值Table 7 Dimensionless RCS average values of each de?tection angle under horizontal polarization

5 結 論

針對穩定器在發動機后向腔體RCS 中為強散射源，在不改變穩定器布局及整體結構前提下，從隱身設計角度，本文研究幾種不同穩定器蒸發腔結構及不同傾斜布置對腔體RCS 的影響，可以得出如下結論：

（1）在非隱身一體化設計的加力燃燒室構成的發動機排氣腔體RCS 中，穩定器采用隱身措施后降低其雷達散射貢獻將直接提高發動機后向雷達隱身性能。

（2）幾種針對某型蒸發管式蒸發腔的修形，都能相比原有結構構成的腔體RCS 有所縮減，統計角域[0°,45°]的均值，在高頻時最大縮減3.4 dB，在低頻時最大縮減1.2 dB。穩定器蒸發腔結構的不同會帶來高頻下腔體RCS 差異較大，低頻下RCS差異較小。

（3）具有橫向和縱向復合角度傾斜的平板結構蒸發腔（WDQ5）對于腔體RCS 的縮減具有一定優勢。同時，平板結構也能相對于原有蒸發管式蒸發腔改善吸波涂層等功能材料的使用工況，提高功能材料的使用可靠性。

（4）穩定器傾斜布置對腔體RCS 有縮減效果，不同傾斜角狀態下的RCS 角向分布規律相似，且在水平極化下穩定器傾斜對腔體RCS 變化較為敏感。綜合考慮穩定器隱身設計及穩定燃燒功能需求，穩定器向噴管出口端傾斜更有利穩定燃燒，優選0°～20°范圍穩定器傾斜布置可對腔體RCS 有較好的抑制效果。