基于Virtual.Lab 的燃油泵調節器結構的模態分析

何立強，王 鵬，胡學滿

（1.中國航空發動機集團有限公司，北京 100097；2.中國人民解放軍陸軍裝備部航空軍事代表局駐上海地區航空軍事代表室，上海 200000；3.廈門大學機電工程系，廈門 361102）

燃油泵調節器作為航空發動機控制系統的重要組成部分，其性能決定著飛機飛行的安全性和可靠性。調節器經常工作在齒輪離心泵高轉速、活門周期運動造成的振動沖擊等惡劣條件下，實際工況下外載荷的傳遞累加到一定程度，引起共振，調節器結構發生疲勞破壞影響其使用壽命，嚴重時導致飛機飛行故障。模態是振動的固有屬性，其分析結果為調節器的性能評價、結構分析優化、故障診斷預報和實際安裝方式等提供了重要基礎支撐。現有的模態分析技術可分為實驗分析與理論計算兩大類，實驗分析需要具備特定的實驗條件，且無法得出任意環境激勵下系統的模態特性。理論計算應用最為廣泛，其中，物理模型將系統看作由理想剛性體組成的多自由度系統，計算精度有限且僅適用于剛性足夠大的研究對象。有限元模型將結構離散為有限個單元，模型參數的設置直接影響其分析結果［1］，參數的修正需要對子結構逐一驗證校核，其過程增加了分析成本。而且直接有限元建模會使求解系統規模龐大，求解極易不收斂，如何實現模型的縮減，必將成為今后研究的重點。傳統的子結構法和動態子結構法，從結構特點出發，將整體拆分再組合的方式，建立整體有限元模型［2?3］，結合實驗模態參數識別子結構界面連接剛度，提高參數識別的精度［4］。燃油泵調節器本身結構緊湊，零件繁多且體積較小，再將其劃分更小的子結構，會使實驗條件變得更苛刻，實驗的精度難以保證。所以，對復雜中小型結構，本文采用關鍵子結構驗證結合整體有限元建模的方法對燃油泵調節器系統進行動力特性分析。

調節器由離心泵、齒輪泵、多個活門和電磁閥等組成，零件數量龐大，零件間的連接建模是整機建模的關鍵。最初的模態分析常以一體化方式進行處理，隨著有限元商業軟件的發展，處理連接的方式也豐富起來，多種連接單元，如Rod、Rigid、Screw、Spring、Gap 等 使 得 連 接 多 樣化，結合部的模擬從彈簧阻尼單元模型發展到多種接觸模型，以及最能模擬結合面特性的各向同性虛擬材料法和薄層單元法等。這些方法在汽車車身、發動機等動態特性分析中得到了廣泛運用［5?10］。但以上模擬結合面的方法過程煩瑣，處理不當容易造成求解矩陣“病態”，本文采用基于閾值的多點約束（Multipoint con?straint，MPC）方法處理結合面，求解易收斂且結果可信度高。

本文基于Virtual.Lab 實現調節器的系統級建模和動態特性分析，利用Virtual.Lab 和Test.Lab可以實現燃油泵調節器設計與分析一體化，且實現過程效率高、結果可視化強、準確性高。Virtual.Lab 是一個開放的環境，實現了與CAD、CAE 和實驗的無縫連接軟件，具備設計流程自動捕捉和管理，完全實現參數驅動，將產品的關鍵設計屬性嵌入到設計流程，在概念設計階段不斷進行改進，成倍縮小了產品開發周期［11］，其豐富模塊和求解器可應用于不同的分析類型，如機械結構振動噪聲和耐久性分析等，適用于航空、汽車等領域尤其在航空領域廣泛應用。

1 模態分析理論

模態分析的過程是由物理模型到模態模型，即以構建質量、阻尼、剛度為參數的關于位移的振動微分方程，求解其特征值和特征矢量，特征值對應模態頻率，特征矢量對應模態振型。簡單系統的方程矩陣具有良好的對稱性，求解容易。復雜系統所建立的微分方程存在耦合關系，可通過坐標變換將耦合系統轉化為非耦合系統，再將求得的結果進行坐標變換轉化為物理坐標下的結果。

將燃油泵調節器看成一個多自由度的振動系統，構建其一般運動微分方程

式中：M、C、K分別為系統質量、阻尼和剛度矩陣；z為位移矢量，其維數等于系統自由度；F為系統的載荷矢量，F=0時，系統處于自由狀態。

不考慮系統的結構阻尼情況下，系統自由模態的運動微分方程變為

對于節點位移矢量的定義，有

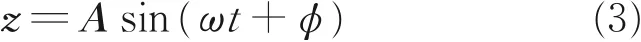
式中：A為特征矢量，ω為固有頻率，φ為初始相位。

對式（3）進行二次求導得

綜合式（2～4），得出最終無阻尼自由振動系統求解方程為

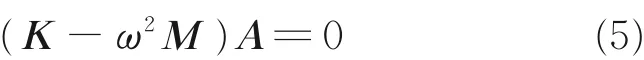
2 復雜結構模型的預處理

該型燃油泵調節器高集成化和復雜化，主要由導葉控制模塊殼體、流量控制模塊殼體、壓差活門、計量活門、停車活門、增壓活門、齒輪泵、導葉和流量伺服系統、物理溫度轉速壓力傳感器和作動筒活塞執行機構等組成。

2.1 三維模型簡化原則

嚴格按照實際情況建立有限元模型的工作量是龐大的，前期對模型的簡化能夠提升仿真計算的效率。對燃油泵調節器三維模型的簡化遵循以下原則：

（1）尺寸優先原則。優先保留殼體、齒輪、活門等尺寸相對較大零件。抑制螺套、墊圈、密封環等尺寸相對較小零件。

（2）功能優先原則。保留螺釘、彈簧等連接功能，具體體現為連接的等效。保留非仿真分析所關心的零件質量對整體的影響，具體體現為質量的等效分布。

（3）特征“粗”化原則。工藝上，從定位、避免應力集中等角度出發，會在結構上增加一些復雜特征，這些特征對結構模態的影響可以忽略，對其進行處理，如去倒角、填槽孔等。

2.2 有限元模型網格處理

網格處理在Hypermesh 中進行，采取4 節點四面體和8 節點六面體單元聯合的方法來處理調節器有限元模型，殼體保護罩和蓋板屬于薄壁零部件，一般采用4 節點的二維網格進行處理。邊界的角域以及密集的油道布置等因素限制了整體的最小結構尺寸，確定網格的基本尺寸為2 mm。殼體采用局部加密方式來保證關鍵幾何特征的離散程度，其他零部件采用均勻網格，使結構剛度矩陣和質量矩陣的元素不致相差太大，可減小數值計算誤差［12］。

網格質量方面，使用Nastran 求解時，要求六面體網格的雅可比要大于0.6，四面體網格的坍塌率要大于0.1。除此以外，還要關注網格的長寬比、扭曲度和翹曲度等其他檢驗項。以調節器為例，其三維模型簡化到網格劃分階段，大體的處理思路如圖1 所示，簡化后模型如圖2 所示。

圖1 調節器模型預處理流程Fig.1 Modulator model preprocessing process

圖2 簡化后調節器模型Fig.2 Simplified rear regulator mode

3 關鍵子結構的模態分析及實驗驗證

在確保正確的關鍵子結構的有限元模型基礎上，再把其他零件通過各種連接方式動態地加到子結構上，組成整體有限元模型。殼體質量之和約為整體的40%，且殼體是整個裝置中單體體積最大的零件，因此殼體為關鍵部件，對調節器研究起主導作用。

3.1 殼體主要連接方式的等效建模

3.1.1 螺釘連接等效建模

殼體間是通過螺釘和油道密封圈進行連接的，基于不同的螺釘連接分析需求，可對該連接方式進行簡化處理。Bush 單元模擬螺釘需要準確的螺釘方向剛度值，單元本身無質量屬性。Beam 單元模擬螺釘需要螺釘的材料屬性、作用長度以及橫截面積，單元可以是有質量的。螺釘數量較多情況，其質量分布對結果存在影響，優先選擇Beam 單元進行螺釘的等效建模。圖3 是螺釘連接簡化示意圖，圖3（a）紅色虛線代表Spring 單元，圖3（b）紅色虛線代表Beam 單元。可以看出，用Beam 單元模擬螺釘時，耦合節點分別為螺釘頭部中心和螺桿末端的中心，兩節點間距離可以有效模擬螺釘作用長度。

圖3 螺釘連接簡化示意圖Fig.3 Simplified diagrammatic sketch of screw connection

螺釘預緊力作用下，殼體的連接狀態變得更“緊密”，這種“緊密”程度用連接區域的等效剛度來衡量，其值可以通過實驗進行參數識別或經驗公式計算所得，螺釘的剛度KS和連接區域的等效剛度KL共同作用下，決定了螺釘連接下的裝配剛度K。KL的計算公式為

式中：E為零件的等效彈性模量，DW為螺釘光桿部分直徑，θ為螺釘頭部和零件1 壓緊區域的升角［13］，一般可取30°；L1是零件1 的厚度，一般情況下，通常L1≤L2；DY為壓緊區域的直徑。壓緊區域DY和連接區域DL存在以下近似關系

Beam 單元模擬螺釘時，用Rbe2 單元模擬除軸向外其他兩個方向的剛度，如圖3 綠線所示，上節點耦合螺釘圓環狀壓緊區域上所有節點，下節點耦合零件2 螺紋孔內壁所有節點。連接區域同樣用Rbe2 單元模擬除軸向外其他兩個方向的剛度，上下節點分別耦合零件1、2 的圓環狀裝配區域，黃線代表具有等效連接剛度的單元。節點間無法完全對應時，采用圖3（a）耦合節點方式處理。

3.1.2 密封圈等效建模

為保證調節器裝配后的密封性，通過安裝密封圈來防止油泄露。忽略密封圈質量，密封處看作兩部分無相對運動，對應節點剛性直接相連即可。Virtual.Lab 振動與噪聲模塊支持組和組之間創建Generic Rigid Connection 來適應節點不完全對應情況，等效模型如圖4 所示。

圖4 密封圈連接簡化示意圖Fig.4 Simplified diagrammatic sketch of sealing ring con?nection

3.2 殼體模態計算

流量控制模塊殼體和導葉控制模塊殼體采用材料AlSi10Mg，其泊松比為0.33，相對密度為2.602 g/cm3，彈性模量為69 GPa。殼體的螺釘規格為HB 1?201F?M8X24，材料為1Cr17Ni2，其泊松比為0.28，相對密度為7.75 g/cm3，彈性模量為210 GPa。通過式（6）求解連接區域等效剛度KL為7.304×108N/m，代入仿真模型進行計算。

定義分析類型為模態分析、求解方法采用SOL 103?Lanczos，計算時不施加任何約束，求解自由狀態下的模態。兩個殼體裝配下的前5 階模態計算結果如表1 所示。

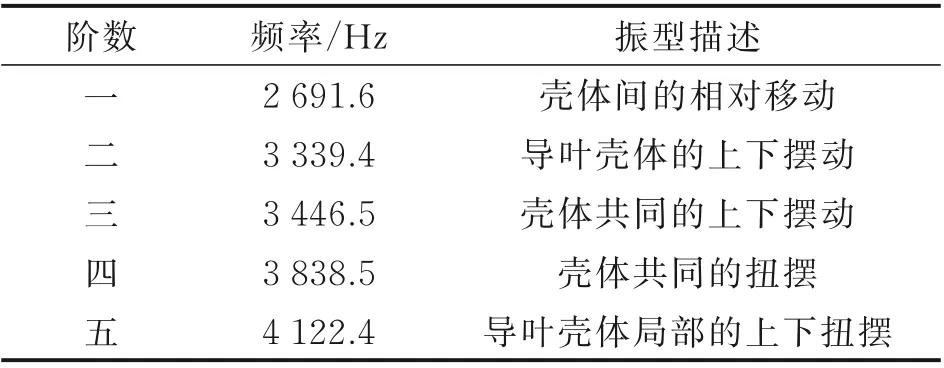
表1 殼體裝配體模態分析結果（連接區域彈簧等效）Table 1 Modal analysis results of shell assembly (spring equivalent in connection area)

從表1 結果來看，經驗公式計算所得連接區域等效剛度值較小，第一階模態振型是殼體間明顯的相對移動，為保證調節器的安全性和可靠性，調節器裝配的過程中會使用較大的預緊力來防止松動。視連接區域“永不分離”，采用Rbe2 代替彈性單元，前5 階模態計算結果如表2 所示。

表2 殼體裝配體模態分析結果（連接區域Rbe2 等效）Table 2 Modal analysis results of shell assembly (Rbe2 equivalent in connection area)

對比表1 的計算結果，連接區域剛度的增加，使得殼體間不再發生相對移動，整體模態頻率都有所升高，通過模態實驗結果可驗證以上兩種建模思路哪一種更加合理。

3.3 殼體模態實驗

3.3.1 實驗設計

圖5 模態實驗系統Fig.5 Modal experiment modal system

模態實驗系統包括被測對象、激勵系統、傳遞路徑測試系統和數據分析系統等，其模型如圖4 所示。設置采集信號頻帶帶寬為5 000 Hz，分辨率2.5 Hz，平均次數設為5 次，將平均響應函數作為測量結果，減小實驗誤差。采用單輸入多響應錘擊法（Single input，multiple output，SIMO），通 過PCB086D05 型力錘進行激振，加速度傳感器將響應點加速度信號轉換成電信號到傳遞路徑測試系統SCM209，采集系統將電壓信號轉化為數字信號輸出。最后，通過LMS.TEST.LAB 進行數據處理和分析數據后處理。

本實驗在殼體上共布置了42 個測點，圖6 為線框模型。激勵點選擇在放氣活門蓋工裝位置（Sheel：1），分別對X、Y、Z三個方向激勵，選擇激勵和響應之間相干性較佳數據進行分析。

圖6 殼體模態實驗線框模型Fig.6 Wireframe model of shell modal experiment

3.3.2 實驗結果

模態置信準則（Modal assurance criteria，MAC）可用于研究同一組中各估計模態的正確性。模態振動向量ψr和ψs之間的MAC 數學模型為

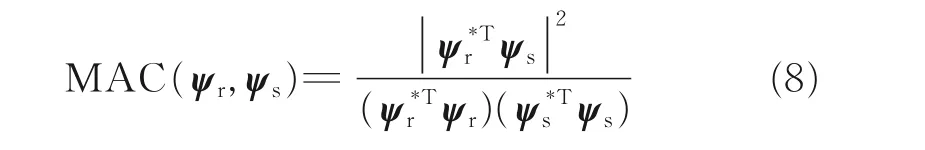
如果是ψr和ψs同一相似物理振型的估計，MAC 就應當趨近1，如果ψr和ψs是不同相異物理振型的估計，MAC 應該很小。通常，MAC＞0.9，認為兩個模態近似，如果MAC＜0.9，認為兩個模態不同，當MAC 值趨近于0 時，認為模態之間是相互獨立正交的。本次實驗所得的前5 階MAC 值矩陣為

除對角線外的MAC 值，最大為9.878%，可以認為本次實驗所得模態參數在可接受范圍內，并未發生模態振型混亂的現象。如果出現非對角線MAC 值較高，振型發生混亂的情況，可以減少振型相似的測點，增加導致振型產生差異的測點來進行糾正［14］。

3.4 計算結果和實驗結果對比

計算和實驗模態的振型大體一致，受篇幅限制，本文未給出振型對比圖，僅給出計算和實驗結果的誤差，如表3 所示。

前5 階模態頻率的數值差雖然在100 Hz 左右，最大為209.33 Hz，但絕對誤差都在5%以內。非線性網格選取的是一階單元，相比高階單元，計算精度偏低，其效果體現在計算值偏大，其次材料屬性誤差等也會造成仿真結果偏大。綜合評價：計算和實驗模態誤差本身不大，有限元模型可信度高，實驗數據較準確。

4 燃油泵調節器整體模型等效及模態分析

燃油泵調節器無油狀態下的模態分析結果是一種近似的結果，對其進行模態計算時，先要假定內部活門處于一固定位置，作動筒被拉至最頂端，以便求得其最危險位置的頻率。

4.1 其他主要連接方式的等效建模

將調節器的其他零件，如軸承、齒輪、活門及活門襯套、伺服閥等有效地、動態地和殼體連接起來，組成整體的有限元模型。除螺釘連接外，還存在其他連接方式，如彈簧連接、緊密連接和滑動連接等。彈簧連接用一個Spring或者Bush表示即可，建模簡單。

4.1.1 相鄰零件松、緊連接的建模

燃油泵調節器的零件多以壓緊或者滑動的方式裝配，軸承內圈和齒輪軸的過盈配合，軸承外圈和殼體的過渡配合及活門襯套和殼體間的緊配合等均為壓緊連接。活門襯套和活門、LVDT 和LVDT 保護罩等都是通過滑配的方式連接。滑動連接采用壓緊連接的相同處理方式，本文處理方法MPC 法，其模型如圖7所示。零件①采用大尺寸網格，零件②采用小尺寸網格。主節點為零件①的1、2、3、4，從節點為零件②的1′、2′、3′、4′、5′、6′。通過設定閾值完成連接，以主節點為圓心，閾值R為半徑，從面上所有圓內節點為從節點，優先選擇距離最近的點相連。壓緊連接時，為使解析面上盡可能多的節點進行連接，閾值盡量取較大值，滑配可以選擇較小的閾值。以典型活門和襯套為例，如圖8 所示，中間高亮部分為使用MPC連接后的解析面。

圖7 非協調網格MPC 連接示意圖Fig.7 MPC connection diagram of different element types

圖8 實體MPC 連接（襯套和活門）Fig.8 Solid MPC connection (bushing and valve)

4.1.2 非敏感零件的簡化建模

對非敏感零件的簡化很大程度上能夠縮減求解模型，僅考慮其質量分布對整體的影響，采用集中質量法是目前最常見的處理方式，通過加權平均單元RBE3 將質量平均分配到部件連接處。以伺服閥為例，對其采取稱重和幾何尺寸估算的方法，確定集中質量參數，加入到殼體零件的螺釘安裝孔上。

可簡化為集中質量的部件還有止動釘、密封環、自沖刷油濾骨架、傳感器和彈簧座等。

4.2 整機模態實驗

整機的模態實驗原理和試驗系統與殼體實驗一致，根據多體耦合下裝置模態可能發生的變化，應在鋁合金保護罩、線性可變差動變壓位移傳感器（Lin?ear variable differential transformer，LVDT）保護罩和各端蓋等子結構的模態布置測點，并考慮子結構安裝后對傳感安裝限制等客觀條件，合理調整測點位置。本實驗共布置了35 個測點，線框模型如圖9所示，激勵點仍選擇在放氣活門蓋工裝位置（ASS：1）。

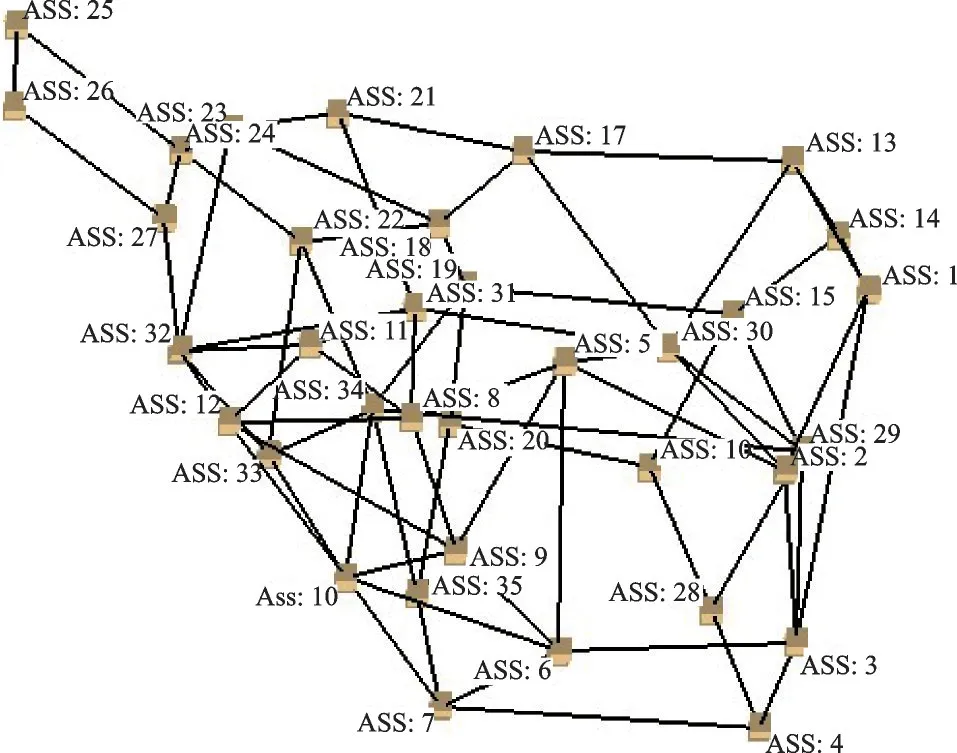
圖9 整機模態實驗線框模型Fig.9 Wireframe model of complete equipment modal ex?periment

實驗在外界干擾較小的室內進行，為了方便懸掛，先用細鐵絲將裝置綁定，通過彈性繩從鐵絲穿過，再將彈性繩綁定到支架上，實驗布置現場如圖10 所示。實驗將分5組進行，每組采集7個點的加速度，每個方向每組錘擊5次，測試頻帶帶寬設置為5 000 Hz，分辨率2.5 Hz。所有測點測完后，對相干性不佳的測點進行補測檢查相干性并及時進行補測。

圖10 整機模態實驗現場Fig.10 Complete equipment modal experiment site

4.3 模態計算結果和仿真結果對比

經質量校正，最終有限元模型的質量約為7.613 kg，與實驗模型的7.81 kg 相比，誤差為2.5%，屬于誤差可接受范圍。根據實驗結果，從計算結果中找出2 000 Hz 以內期望的模態和振型，其誤差如表4 所示。

表4 燃油泵調節器計算模態和實驗模態對比誤差Table 4 Comparison error between calculation mode and experimental mode of fuel pump regulator

對1 000 Hz 頻段內模態信息進行分析：調節器模態計算結果所得結構基頻為519.6 Hz，實驗所得基頻為512.7 Hz，兩者相對誤差為1.3%，振型均體現為LVDT 保護罩的彎曲，振型對比圖如圖11 所示。仿真和實驗的第二、第三階模態頻率分布在550 和650 Hz 附近，振型相似，主要體現為電插座和蓋板處的扭動。以第三階模態振型為例，如圖12 所示，裝置其他位置，如LVDT 保護罩、殼體保護罩和活塞末端均有輕微的變形。從第四階開始，振型開始集中體現為殼體保護罩的呼吸模態，不同階次振型為殼體保護罩各個面的彎曲模態，如圖13 所示，并伴有活塞末端和連接件的擺動，由于實驗部分并未在活塞遠端布置傳感器，其振型無法對比。

圖11 第一階模態振型對比Fig.11 Comparison of the first mode shapes

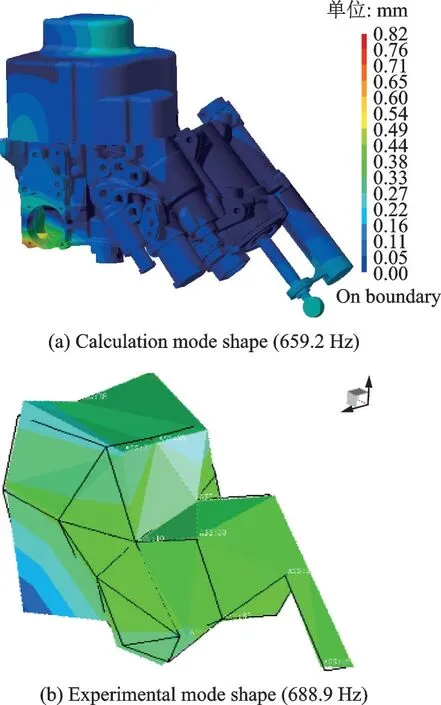
圖12 第三階模態振型對比Fig.12 Comparison of the third mode shapes

圖13 第四階模態振型對比Fig.13 Comparison of the fourth mode shapes

1 000～2 000 Hz 以內，仿真結果顯示1 150 Hz左右為傳動軸的彎曲模態，1 200 Hz 以上的振型為殼體保護罩和傳動軸共同的彎曲模態，實驗所得結果和計算結果之間絕對誤差均在10%以內，由于實驗并未在傳動軸布置傳感器，傳動軸上的振型無法對比。實驗和計算的1 600 Hz附近振型開始體現為殼體保護罩的二階彎曲，取第八階振型進行對比，如圖14所示。1 600 Hz以上實驗所得振型均為殼體的彎曲模態，而仿真結果在1 812 Hz 出現了蓋板的彎曲模態。

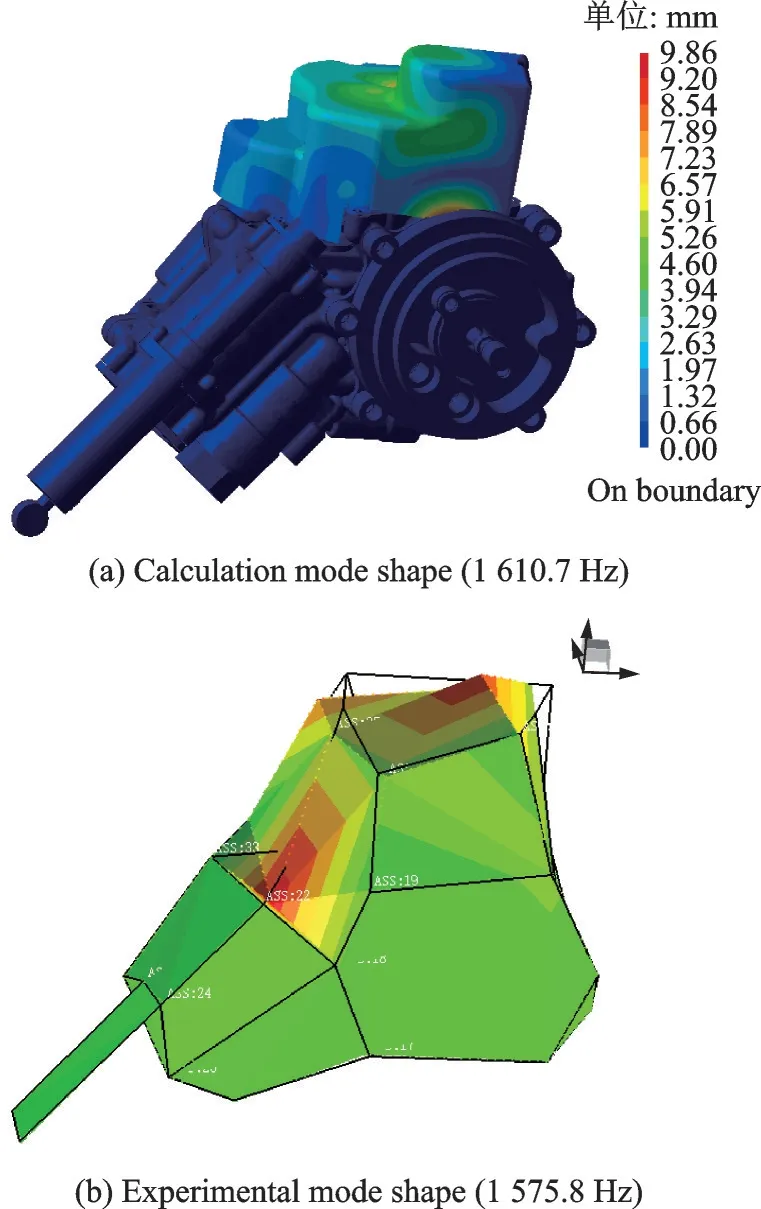
圖14 第八階模態振型對比Fig.14 Comparison of the eighth mode shapes

實驗系統由彈性繩?試件組成，其固有頻率小于試件的第一階固有頻率，仿真基頻大于實驗的基頻，這是因為實驗狀態是一種近似的自由狀態，而有限元模態分析的仿真模型采用理想的自由狀態。隨固有頻率的升高，振型依次體現為LVDT保護罩的彎曲模態、電插座附近的扭轉模態、殼體保護罩的一階彎曲模態、傳動軸的彎曲模態和殼體保護罩的高階彎曲和扭轉模態。活塞桿的末端通過連接件和LVDT 的末端相連，連接處在1 000 Hz 以內和1 000～2 000 Hz以內均可能出現單獨的彎曲模態或與其他局部模態共同體現。越往高頻，尤其是1 500 Hz 以上，保護罩X、Y、Z三向上的呼吸模態約明顯。

燃油泵調節器在0～2 000 Hz，振型主要為局部模態，頻率平均誤差小于4%，特別是在低頻段，誤差更小，在工程要求上屬于可接受誤差，滿足工程要求。所以，有限元模型等效建模具有一定有效性，模態計算結合實驗驗證對燃油泵調節器的動態特性研究具有指導意義和參考價值。本次分析對象存在大量輕質薄壁結構和細長結構，且與裝置主體距離較遠，從提高整體的固有頻率角度出發，可對結構進行加強，縮短零件的延伸長度。

5 結 論

本文以燃油調節為研究對象，詳細介紹了中小型裝備模態分析方法。從三維模型的簡化處理到有限元模型的等效建模，將計算模態與實驗模態進行對比，基于正確的子結構有限元模型進一步建立有效的整體有限元模型，為燃油泵調節器的動力響應提供可靠依據。從分析的結果來看總結歸納，得出以下結論：

（1）復雜結構的有限元分析過程中，三維模型的簡化以及有限元網格處理直接影響求解精度。特征處理是否恰當，模型離散化程度是否合理都可作為模態分析的重要研究內容。

（2）對子結構建模的有效性驗證是整體有限元模型正確的前提。對子結構模型的反饋和修正可以降低整體模型處理和修正的難度。

（3）對調節器中螺釘、密封圈、彈簧、緊配合和滑動配合建模，目的是為了模擬真實的裝配狀態，螺釘連接需要考慮在預緊力下產生的等效連接剛度，壓緊和滑動配合采用MPC 技術，實現不同單元類型網格的過渡問題，不易造成求解不收斂，從而提高了求解效率，適用于有小變形位移的大規模復雜有限元模型。

（4）受實驗條件限制，實驗結果振型體現不完整，但整體的分析效果良好。進一步提高模型等效程度和實驗數據的信服度是提升仿真精度的關鍵。