基于科普拉函數的電、熱負荷及風電出力間的相關性分析與建模

楊 柳，李 明

(國網通化供電公司，吉林 通化 134001)

隨著我國大規模的風電并網，給電網的運行也帶來了一定的沖擊，風電與熱、電負荷在時間和空間上均可能存在較強的相關性，如果不考慮這種關系將會影響風電的合理消納及風能的利用效率[1-2]。因此，在電網經濟調度中有必要對風電與熱、電負荷間的相關性進行精確建模，以量化變量的隨機性給電力系統帶來的影響，實現電網安全經濟運行。

研究變量間的相關性問題的關鍵在于正確處理非正態隨機變量之間的相關性[3]。 科普拉(Copula)理論作為多元分析方法中的一種方法，能較準確描述多元變量的相關結構，被廣泛應用于兩個(或多個)隨機變量的依賴結構建模。該方法被用于許多領域的研究，包括金融[4]、風電場相關性分析[5]、洪水風險分析[6]、頻率分析等[7]。文獻[8]提出構造混合Copula函數來模擬兩個風場之間的風速相關性，但沒有關于模型結構和驗證的細節。文獻[9]基于動態Copula理論構建風光聯合出力模型，用動態相關系數來描述相關性，并將其運用于數據驅動的風光聯合系統中。文獻[10]采用的是線性相關性建模，這對于非線性的變量無法準確地描述。鑒于此，本文提出采用Copula函數來推斷Copula參數及構建風-電-熱相關性模型。以某地區的熱負荷、電負荷和風電出力作為數據樣本，驗證Copula建模的有效性，結果表明所提方法的準確性和合理性。

1 Copula理論及相關性評價指標

1.1 Copula理論

Copula是一個無論其單變量分布如何，“連接”或“耦合”兩個或多個與時間無關的變量的數學函數。設H是具有邊際單變量分布F和G的聯合累積分布函數，X和Y是連續的二維隨機變量。斯科拉(Sklar)定理指出當F和G連續時，存在唯一一個確定的Copula函數C(·)滿足：

H(x,y)=C[F(x),G(y)]

(1)

Sklar定理也可以推廣到多元分布的聯合分布函數。

1.2 相關性指標

在非正態分布情況下，需要引入能夠很好測量隨機變量相關性的指標，通常通過參數和經驗依賴性度量之間的理論關系來估計，如肯德爾(Kendall)秩相關系數τ和斯皮爾曼(Spearman)相關系數ρ，若τ>0，表示變量間呈正相關；τ<0，表示變量間呈負相關[11]。ρ相關系數也呈同樣的變化關系。設兩隨機變量X，Y的分布函數分別為F(x)，G(y)，若u=F(x)，v=G(y)，則兩變量之間的相關性可由τ和ρ相關系數得到，即：

(2)

(3)

2 基于Copula函數變量相關性分析與建模

Copula模型的一個顯著優點就是變量的邊緣分布不受限制，它可以將邊緣分布和變量間相關性分開研究，所以由Sklar定理將Copula函數模型的建立分步來完成：第一步，確定變量的邊緣分布，由變量的歷史數據可確定邊緣分布；第二步，選取適當的Copula函數，只有選取合適的Copula函數才能準確的反應變量之間的相關結構；第三步，參數估計，得出Copula函數模型中的未知參數估計值。

2.1 邊緣分布估計

一般情況下，邊緣分布的確定有兩種方式，一種是參數方式，另一種是非參數方式。參數方式是指假設隨機變量服從某一確定的分布，比如一些常用的分布，然后根據極大似然估計法估計分布中的參數，最后進行檢驗；非參數方式是指不需要事先假設隨機變量服從哪種具體形式，而是以經驗分布與核密度估計為基礎，將經驗分布代替整體隨機變量分布，最后采用極大似然估計方法對模型的參數進行估計。在實際中，邊緣分布的確定對變量間的相關性分析是十分重要的，如果選取不當，將會影響最終數據的擬合效果。所以本文采用非參數方式，基于核密度的估計方法來確立隨機變量的邊緣分布，對于已知的數據樣本，核密度估計的結果主要取決于窗寬h的選擇。設隨機變量X的樣品點為(x1，x2，…，xn)，n為樣本個數，在任意點x處的概率密度函數f(x)的核密度估計為：

(4)

其中h為窗寬或帶寬，K(·)為核函數，起到一種加權作用，任一點x處的密度函數估計值的大小與該點附近所包含的樣本點的個數有關，若樣本點較稀疏，則估計值較小，反之則較大。對f(x)積分可以得到變量的邊緣分布函數F(x)，再將邊緣分布函數轉換為均勻分布U，對于r∈(0，1)存在：

P[F(x)≤r]=P[X≤F-1(r)]=

F[F-1(r)]=r?F(x)=U

(5)

2.2 Copula函數模型的確定

最優Copula函數的選取包括兩個方面，一是Copula函數參數的確定，二是Copula函數類型的確定。選取合適的備選Copula函數的方法有很多種，根據分析數據的特點來選擇合適的備選Copula函數。本文采用圖形法，通過二元頻率直方圖來選擇合適的備選Copula函數。如果兩變量的二元頻率直方圖是非對稱的，則可以選擇岡貝爾(Gumbel) Copula函數和克萊頓(Clyton) Copula函數，如果是對稱的，則選擇法蘭克(Frank) Copula函數、Norm Copula函數和t-Copula函數；如果二元頻率直方圖反應尾部的相關性，則可以選擇Gumbel Copula函數、Clyton Copula函數和t-Copula函數，如果不反應尾部相關性，則選擇Frank Copula函數和Norm Copula函數。在得到的各Copula函數所對應的最優參數的基礎上，通過平方歐式距離檢驗模型的擬合度，將平方歐式距離最小的備選Copula函數作為最優Copula函數。

2.3 參數估計

在確定了邊緣分布和最優Copula函數后，通過原始數據和選取的Copula函數進行模型的參數估計，采用分步極大似然估計法對變量間的Copula未知參數進行估計。根據式(6)可知，采用分步極大似然估計法進行估計，步驟為：

(6)

a.求參數θ1和θ2的極大似然值:

b.把θ1和θ2帶入下式，求出Copula函數中的參數α：

3 算例分析

本文選某地一年的風力發電和電、熱負荷的數據進行分析，它代表了在某地區一年中熱負荷和電負荷的基本趨勢和風電場輸出功率的波動情況，算法流程見圖1。目前變量間的相關性分析僅考慮在二元變量間進行分析，所以風-電-熱三變量需要分成兩兩一組進行分析。

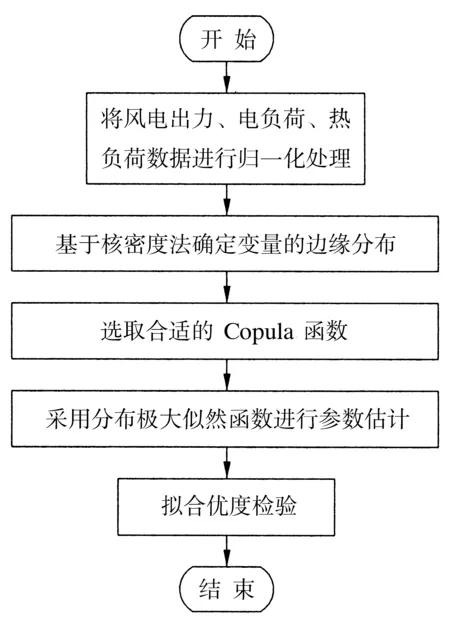
圖1 算法流程

3.1 確定變量的邊緣分布

采取基于核密度的估計方法來確立隨機變量的邊緣分布，其不需要事先假設隨機變量服從哪種具體形式，只從數據本身出發，通過與經驗分布對比檢驗核密度估計的準確性。圖2分別為電負荷、風力發電和熱負荷的經驗分布函數和核分布估計圖，由圖2可知該方法可以很好地擬合樣本數據，所以核密度估計是準確的。

圖2 邊緣分布函數

3.2 選取合適的Copula函數

在確定了電負荷、風力發電和熱負荷的邊緣分布后，繪制電負荷和風力發電、電負荷和熱負荷、風力發電和熱負荷的二元頻率和頻數直方圖，由于篇幅有限，僅對電負荷和風力發電進行分析，其余兩組分析方法相似。電負荷和風力發電的頻率直方圖見圖3，從圖3中可以看出電負荷和風電出力的二元頻率直方圖具有基本對稱的尾部，所以初選Norm Copula函數和t-Copula函數來描述變量之間的相關結構。

圖3 電負荷和風電出力的頻率直方圖

3.3 參數估計

確定了變量的邊緣分布和選取合適的Copula函數后，通過各變量的原始數據，采用分布極大似然估計法對所選取的Copula函數進行參數估計，表1為電負荷和風電出力模型估計所得到的參數，其中皮爾森(Pearson)系數用來描述變量間的線性相關程度，Kendall秩相關系數表示隨機變量間變化趨勢一致相關性，Spearman秩相關系數表示隨機變量間變化趨勢一致與不一致的概率之差倍數，自由度為t-Copula模型中的參數，平方歐氏距離反映了Copula函數模型擬合的情況，數值越小，代表模型擬合的越好，圖4和圖5為得到的模型。

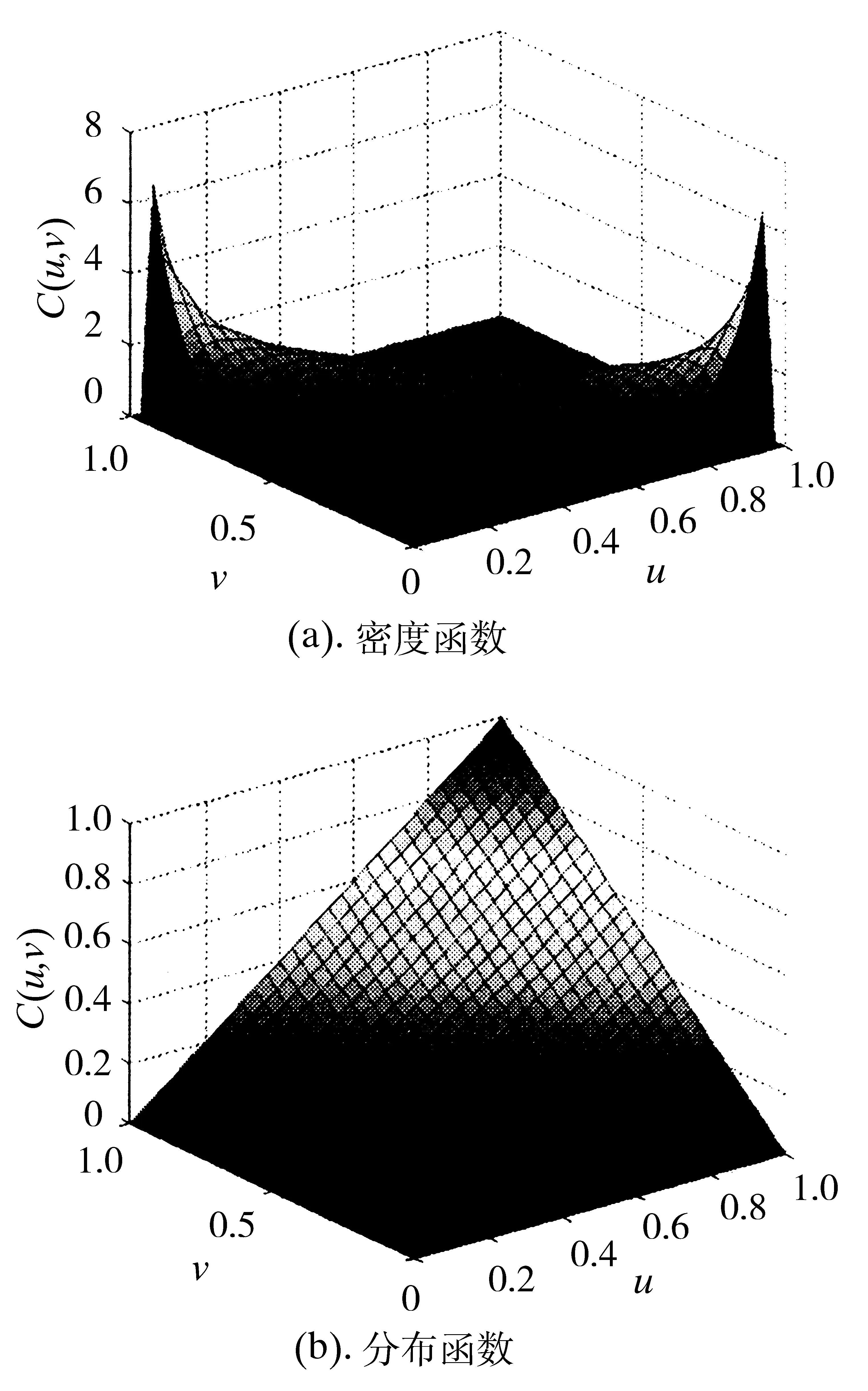
圖4 電負荷和風電出力Norm Copula密度函數和分布函數

圖5 電負荷和風電出力t- Copula密度函數和分布函數

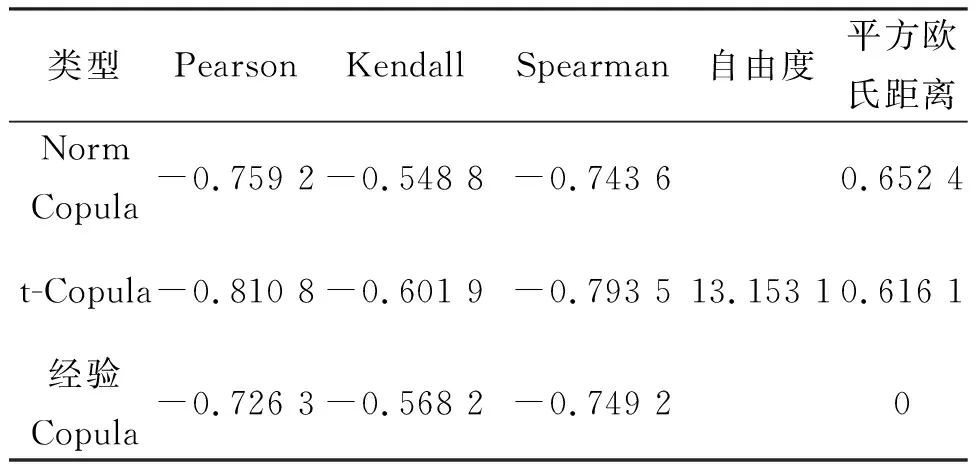
表1 電負荷和風電出力的參數估計

3.4 模型評價

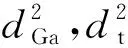
(7)

從圖4和圖5可以看出，電負荷和風電出力中的二元t-Copula函數的密度函數比二元Norm Copula函數的密度函數具有更厚的尾部特征，說明t-Copula函數可以更好地擬合電負荷和風電出力之間的相關關系。

4 結論

熱負荷、電負荷和風電出力三者之間的相關性對于風電合理消納、提高風能利用效率具有重要的意義。本文以Copula理論為基礎，首先確定變量間的邊緣分布，然后采用分布極大似然法對模型進行估計，最后通過平方歐式距離對所選取的Copula函數模型進行擬合優度檢驗。實例分析表明，t-Copula函數可以更好地描述電負荷與風電出力之間的相關性，并且可以準確地描述變量間的尾部相關性，避免了只關注秩相關系數的缺點。