基于信息熵與改進極限學習機的中長期徑流預測

岳兆新，艾 萍，熊傳圣，宋艷紅，洪 敏，于家瑞

(1.河海大學計算機與信息學院，江蘇 南京 211100； 2.南京工業職業技術大學計算機與軟件學院，江蘇 南京 210023；3.河海大學水文水資源學院，江蘇 南京 210098)

水文中長期預報是指基于水文現象演化的客觀規律，根據前期和歷史水文、氣象等信息，運用成因分析和數學建模等方法，對未來較長時間內水文情勢做出定性或定量預報[1-2]。及時、準確的中長期水文預報可為水資源高效利用、水利工程建設與運行，以及防汛抗旱指揮決策等提供重要的基礎數據和科學的決策依據。當前，中長期水文預報仍然處于探索、發展階段，預報精度還不能滿足各生產部門的實際需求。中長期徑流預測是中長期水文預報中的一個重要研究方向，也是水信息學科研究與應用的重要難題之一。

目前，常用的中長期徑流預測方法主要有成因分析方法、統計學方法、基于智能算法的預測方法和基于數值天氣預報的預測方法四大類。其中，成因分析方法[3]和統計學方法[4-5]是水文學科的典型方法，具有一定的適用范疇，但也存在諸多需要研究的問題。比如影響徑流序列長期變化的物理成因復雜，難以完全掌握其客觀規律。而統計學方法多以線性方法為主，難以適應徑流變化影響要素的復雜非線性特性，具有一定的局限性。基于智能算法和數值天氣預報的綜合預測方法是近些年發展起來的新方法，是伴隨計算機信息技術的發展和新數學建模方法的涌現而發展起來的新技術。前者具有較好的非線性映射、泛化和容錯能力，被廣泛應用于徑流預測領域[6-7]；后者則在水文預報中耦合一定預見期內的數值天氣預報產品，在探索增長徑流預報預見期方面，具有一定的研究意義[8]。基于智能算法的中長期徑流預測模型主要根據輸入輸出變量之間的函數關系構建基于人工神經網絡、支持向量機 (support vector machine, SVM)、小波分析等預測模型或者綜合采用多個模型對未來中長期徑流進行預測分析，并取得了諸多成果[9-13]。盡管上述基于智能算法的預測模型應用廣泛，但模型結構相對復雜，參數在訓練過程中需要初始化以及不斷優化調整，效率相對較低，且 BP神經網絡 (backpropagation neural networks, BPNN)采用基于梯度下降的方法，容易陷入局部最小值問題，算法需要多次迭代，因而整體效率不高。極限學習機[14](extreme learning machine, ELM)是一種單隱層前饋神經網絡，具有參數設置簡單、計算速度快、誤差小、泛化能力強等優點，被廣泛應用于故障診斷、圖像處理等領域。

此外，影響徑流過程變化的關鍵因子篩選也是中長期徑流預測需要研究的重要內容。因子篩選方法主要包括先驗知識法、相關系數法、主成分分析法和信息熵法[15-17]。先驗知識法主要依賴于人工經驗，主觀性較強，具有一定的局限性。相關系數法和主成分分析法，整體上屬于線性方法，難以適應中長期徑流過程影響因子的復雜非線性特性，具有一定的適用范圍。信息熵法，尤其是互信息方法忽略了變量分布，適用于備選因子間的線性和非線性相關關系。偏互信息方法是在互信息方法基礎上的改進，可以有效避免對已入選因子的影響，減少冗余變量，降低計算復雜度。

鑒于此，本文提出一種基于信息熵與改進極限學習機的中長期徑流預測方法。首先，基于不同水文站點的流域控制面積構造徑流綜合指數，在較宏觀層面表征流域水情豐枯變化；其次，采用偏互信息方法計算影響對象與徑流綜合指數之間的相關性，獲得徑流過程變化的關鍵因子集，形成預測模型的輸入；最后，結合K折交叉驗證與改進粒子群算法優化ELM參數，構建IPSO-ELM(improved particle swarm optimization, IPSO-ELM)模型，用于中長期徑流預測。

1 基于信息熵與改進極限學習機的中長期徑流預測方法

1.1 徑流綜合指數構造

粒計算作為人工智能研究領域中的一種新理念方法，其目的是在問題的求解過程中，用粒度合適的“粒”作為處理對象，從而在保證求得滿意解的前提下，提高解決問題的效率[18]。當前中長期徑流預測，主要基于流域內某些典型站點(單一粒度)的徑流變化來預測中長期徑流變化情勢，并沒有結合研究區域內多個水文時空對象進行多粒度綜合分析，導致復雜環境下流域中長期徑流預測的宏觀研判能力不足。因此，本文依據粒計算理論，通過研究分析流域中不同水文站點(細粒度)月平均徑流的一致性，構造描述流域月均徑流豐枯情況的流域徑流綜合指數(粗粒度)，在較宏觀的層面研究整個流域的徑流變化情勢，以提高流域中長期徑流預測的準確性和可靠性。以此為基礎，本文通過研究流域內多個不同水文站點月平均徑流的一致性，構造具有多粒度特性的流域徑流綜合指數(comprehensive runoff index, COM)，以表征流域徑流的豐枯情況。為了避免測站之間的累積影響，更客觀地使用各測站描述流域徑流豐枯情況，本文在確定所選水文站點的權重時，采用削減流域下游水文站對整體指數的貢獻度原則，基于站點流域控制面積構建流域徑流綜合指數。

假設流域站點數量為nS,第i個水文站的控制面積百分比為Si,第i個水文站，第j個月的月平均徑流為cij，則第i個水文站的權重wi和第j個月的徑流綜合指數cj分別為

(1)

(2)

1.2 基于信息熵的因子篩選

互信息(mutual information, MI)以信息熵理論為基礎，既能夠度量輸入變量與預測對象間的線性和非線性關系，也能夠度量一個變量中含有的關于另一個變量的信息量[19]。但采用MI對輸入變量進行篩選時，由于輸入變量之間的耦合關系會對MI的計算結果產生影響，從而導致誤選或漏選。因此，May等[20-21]提出了偏互信息法(partial mutual information, PMI)，通過計算條件期望消除了變量之間的聯系，從而保證了變量選擇的可靠性和準確性。偏互信息定義為

(3)

x′=x-E[x|z]

(4)

y′=y-E[y|z]

(5)

式中：E為期望值；x為備選輸入因子；y為預測對象。

給定N個離散樣本，偏互信息可采用如下離散形式定義：

(6)

1.3 IPSO-ELM預測模型構建

1.3.1極限學習機

假設給定任意N個不同樣本(Xi,ti)。其中，Xi=(xi1,xi2,…,xin)T∈Rn，ti=(ti1,ti2,…,tim)T∈Rm，目標函數定義如下：

式中：g(x)為激活函數；Wi為輸入層與隱含層之間的權重矩陣，Wi=(wi1,wi2,…,win)T；βi為隱含層與輸出層之間的輸出權重矩陣，βi=(βi1,βi2,…,βim)T；bi為第i個隱含層神經元的偏置；oj為第j個樣本的網絡輸出值；C為隱含層神經元個數。

預測值與真實值誤差最小，可表示為

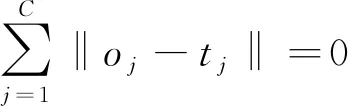
(8)

也就是存在βi、bi、Wi使得：

用矩陣表示為

Hβ=T

(10)

其中H(W1,…,WC,b1,…,bC,X1,…,XC)=

式中：H為隱層節點的輸出；β為輸出權重；T為期望輸出。

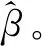
1.3.2結合K折交叉驗證與改進粒子群的ELM參數優化方法

粒子群 (particle swarm optimization, PSO)算法具有算法簡單、收斂速度快、可調參數少、尋優能力強等優勢，但是還存在一些不足[22]：隨機產生初始位置，導致部分粒子位置距離最優解較遠，影響了計算效率；參數設定較大時容易錯過最優解，導致算法不收斂，或者其他粒子可能錯過最優解，進而影響收斂速度和精度；可能出現“早熟”現象，導致局部極值點的出現。為避免出現上述情形，本文首先對PSO算法進行參數改進和變異操作，再以此為基礎，提出結合K折交叉驗證(K-fold cross validation, K-CV)與IPSO的ELM參數優化方法。具體步驟主要包括參數初始化、IPSO適應度函數選取、個體極值與群體極值的迭代更新和ELM最優參數生成。具體如下：

步驟1：初始化。給定訓練樣本[xi,yi] (xi∈RnIP，nIP為輸入神經元個數，i=1,2,…,NIP，NIP為訓練樣本個數)，確定激勵函數，并設置隱含層節點數C。初始化Np,IP個維數為D的參數向量tr,g(r=1,2,…,Np,IP)，其中任意一維的取值范圍為[-1,1]，g表示迭代次數，D=C(nIP+1)。

粒子群種群個體t由極限學習機的輸入權值向量a=(a1,a2,…,ac)和隱含層偏置矩陣d組成，t=(a11,a12,…,a1nIP,a21,a22,…,a2nIP,…,ac1,ac2,…,acnIP,d1,d2,…,dc)。對于每個種群個體tr,g，計算隱含層輸出矩陣H，并計算輸出權重β。

步驟2：適應度函數選取。計算10-CV的均方根誤差作為IPSO的適應度，尋找平均均方根誤差最小的個體。

步驟3：迭代更新。更新位置xi和速度vj，同時引入變異算子，在粒子更新之前有一定的概率初始化粒子速度和位置，計算適應度值，更新粒子的個體極值和群體極值。

步驟4：獲得ELM最優參數。判斷是否達到終止條件(達到適應度值預設精度或滿足最小誤差值或最大迭代次數)，則停止迭代，獲得ELM最優參數組合；否則，回到步驟3。

1.4 評價指標

本文選用水文預報領域常用的評價指標，包括平均絕對百分比誤差Emape、均方根誤差Ermse、確定性系數Edc、相對誤差Ere和合格率Eqr5種，以此綜合評價預測模型的性能。各項評價指標的計算公式如下：

(11)

(12)

(13)

(14)

(15)

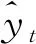
根據GBT 22482—2008《水文情報預報規范》，中長期徑流預報的相對誤差小于20%為合格。

2 實例驗證

2.1 研究區域與數據資料

雅礱江流域位于青藏高原東部，地理位置界于96°52′～102°48′E、26°32′～33°58′N之間，北以巴顏喀拉山與黃河分水，東以大雪山與大渡河分界，西以雀兒山、沙魯里山與金沙江上段相鄰，南接滇東北高原的金沙江谷地。流域東、北、西三面大部分為海拔4 000 m以上的高山包圍，其主峰均在5 500 m以上，南面分水嶺高程較低，約2 000 m左右[23]。雅礱江流域及其站點分布如圖1所示。用于雅礱江流域中長期徑流預測的相關資料包括：①1951年1月—2011年12月，130項大氣環流因子數據(本文選取與雅礱江流域相關的21項遙相關氣候因子)；②1960年1月—2012年9月的氣壓、溫度、濕度、降水、風速、日照等氣象資料；③1960年1月—2016年12月的兩河口、錦屏、官地、二灘水文站徑流資料；④1998年4月—2008年7月的歸一化植被指數(normalized difference vegetation index, NDVI)數據(旬尺度)。

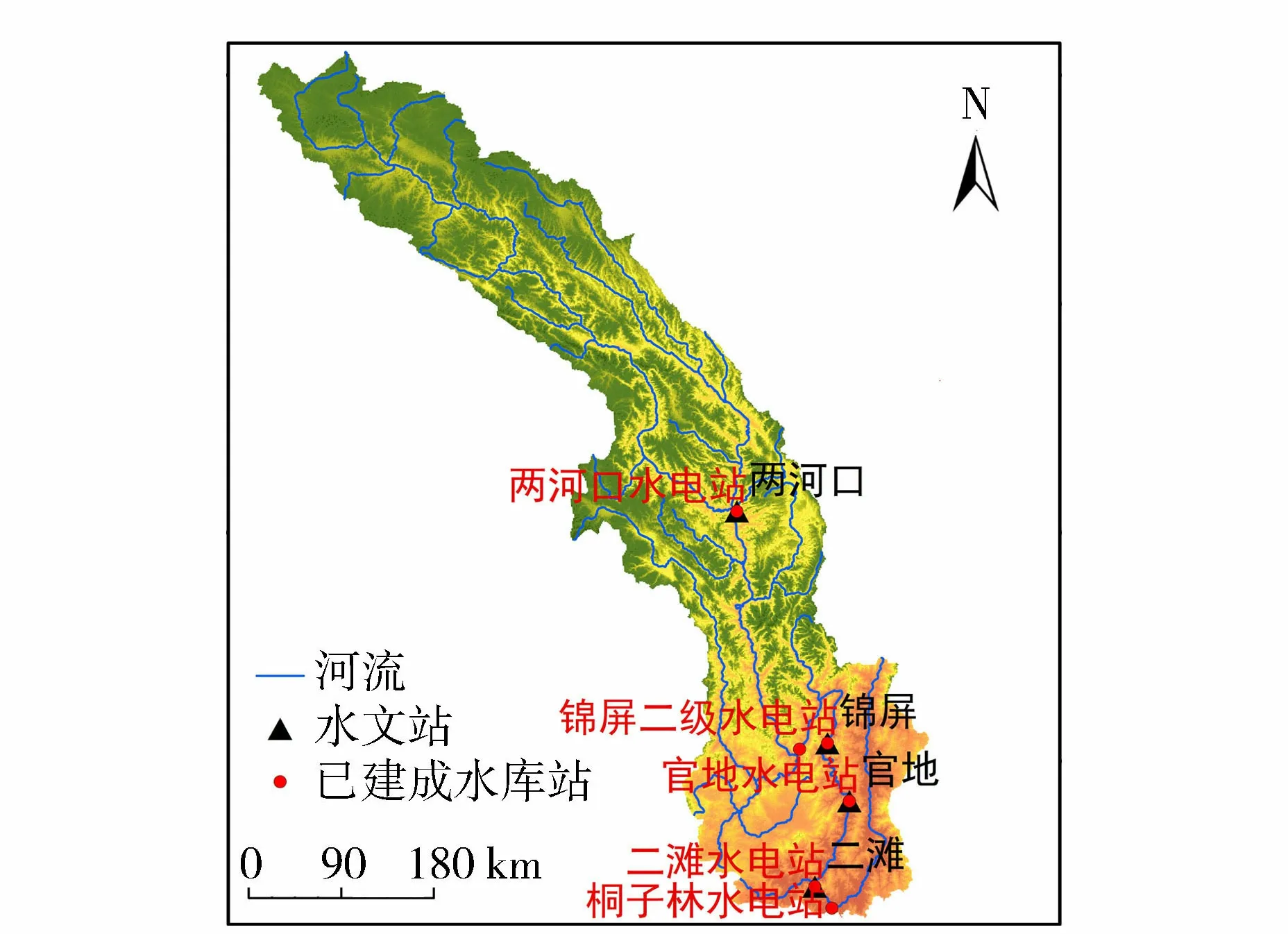
圖1 雅礱江流域及其站點分布

考慮水文時間序列的一致性，以及比較不同水文要素對流域徑流的影響，本文將數據集分為D1和D2兩組。其中，D1數據集時間跨度為1998年4月—2008年7月，包括前期流域徑流綜合指數、面雨量指數、遙相關氣候因子共計124組樣本；D2數據集時間跨度為1998年4月—2008年7月，包括前期流域徑流綜合指數、面雨量指數、遙相關氣候因子，以及植被指數數據共計124組樣本。

2.2 徑流綜合指數構造結果

本文首先對雅礱江流域4個水文站(兩河口、錦屏、官地、二灘)進行月平均徑流一致性分析，結果表明上述站點之間保持著很高的相關性(圖2)，因此基于上述水文站點的月平均徑流(細粒度)，構造流域徑流綜合指數(粗粒度)；然后根據式(1)(2)，計算不同水文站點權重，結果如表1所示；最后構建徑流綜合指數，并與4個水文站的月平均徑流進行Pearson相關性分析，結果表明構建的徑流綜合指數與4個水文站的月平均徑流高度相關(表2)。

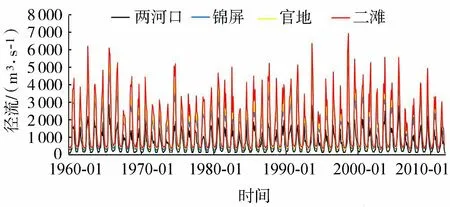
圖2 流域內4個水文站月平均徑流一致性對比

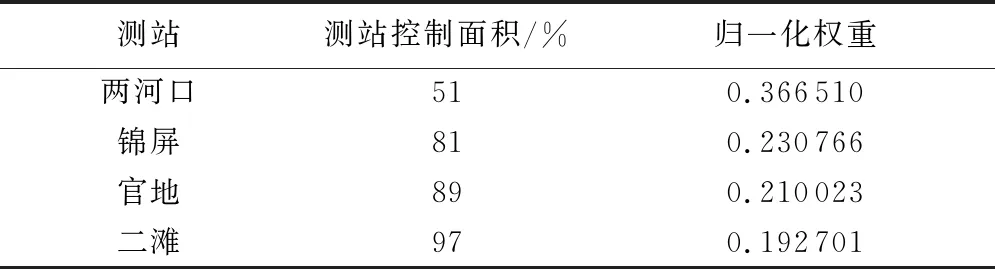
表1 基于4個水文站點流域控制面積構建流域徑流綜合指數權重

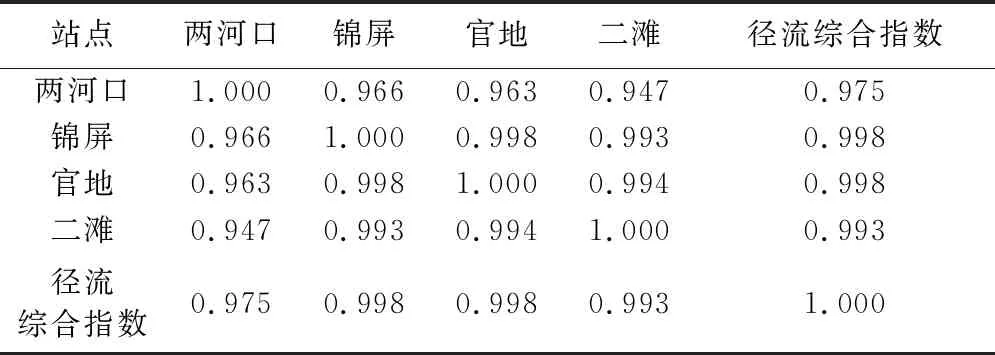
表2 徑流綜合指數與4個水文站月平均徑流量Pearson相關性分析

2.3 基于偏互信息法的因子篩選結果

D1數據集的候選因子包括雅礱江流域徑流綜合指數因子fcom(fcom(t-1)，fcom(t-2), …,fcom(t-12))、面雨量指數因子frain(frain(t-1)，frain(t-2)，…,frain(t-12))，21個遙相關氣候因子fatm1(fatm1(t-1)，fatm1(t-2)，…,fatm1(t-12))，fatm2(fatm2(t-1)，fatm2(t-2)，…,fatm2(t-12))，…,fatm21(fatm21(t-1),fatm21(t-2)，…,fatm21(t-12))等23個對象前期12個月的觀測值作為備選特征，總數為276(23×12)個；D2的候選因子則包括雅礱江流域徑流綜合指數因子、面雨量指數因子、21個遙感相關氣候因子，以及植被指數因子fndvi(fndvi(t-1)，fndvi(t-2)，…,fndvi(t-12))等24個對象前期12個月的觀測值作為備選特征，總數為288(24×12)個。具體如表3所示。

表3 雅礱江流域中長期徑流過程變化影響候選因子

為研究不同水文要素對中長期徑流預測效果的影響，并考慮自回歸項對整個因子篩選的影響太過顯著等特點，基于赤池信息準則方法并不完全適用于雅礱江流域徑流變化過程的因子篩選。因此，本文將在PMI方法基礎上結合人工挑選方式進行因子選擇：采用PMI方法對所有備選因子按照相關性大小進行排序，并在此基礎上分別選擇各自相關性大小排名前20的備選因子；以此為基礎，再通過人工挑選方式分別在D1與D2數據集上選取上述幾類水文對象中相關性大小各自排序前列的因子(最多排名前五)，最終組合形成新的綜合篩選結果。其中，D1數據集篩選后的因子為11個，D2為13個，具體如表4所示。

表4 不同數據集的因子篩選結果

2.4 基于IPSO-ELM模型的流域中長期徑流預測

2.4.1數據集劃分

本文將D1與D2數據集劃分為兩部分，一部分數據用于預測模型的10折交叉驗證(10-CV)，稱為交叉驗證期；另一部分數據用于模型測試。其中，用于10-CV的數據為1998年4月—2006年7月共計100組樣本(隨機選取90組用于訓練，余下10組用于驗證模型)，測試數據為2006年8月—2008年7月共24組樣本。交叉驗證期與測試期數據劃分如表5所示。

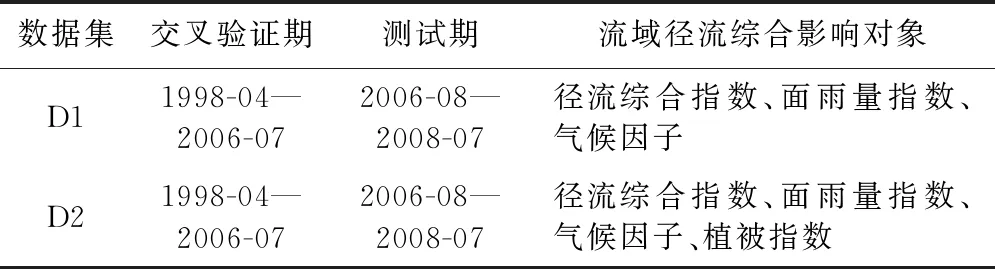
表5 交叉驗證期及測試期數據劃分

2.4.2參數設置

粒子群算法初始化為：種群規模為40，最大迭代次數為400，粒子位置區間為[-2,2]，粒子速度區間[-0.5,0.5]，其他參數設置為c10取值2.2，c11取值1.2，c20取值0.3，c21取值2.2，p0取值0.01，p1取值0.28，w0取值1，w1取值0.1，學習速率為0.1，訓練目標為0.001。適應度函數選擇ELM的10折交叉驗證的平均均方根誤差，ELM的激活函數選擇“sigmoid”。

為了保證對比試驗的可靠性，本文對BPNN和SVM算法進行了相應優化，其初始參數設置分別為：BPNN基于10-CV方法，采用與ELM相同的結構，訓練函數選擇“tansig”，學習函數選擇“logsig”，最大訓練次數為600，學習速率為0.1，訓練采用LM算法，動量因子為0.9，期望誤差為0.001；支持向量機回歸模型選擇徑向基核函數，采用10-CV方法，通過多次試驗尋找最佳參數：徑向基核函數中的σ=0.5，懲罰參數Ca=1，ε=0.001。

2.4.3訓練結果及分析

在10-CV階段，5種預測模型在D1與D2數據集上均具有較好的訓練效果，其中IPSO-ELM模型在Emape、Ermse和Edc3個指標方面整體優于其他4種預測模型，顯示了本文所提算法在該階段具有較好的擬合效果和泛化能力。另外，5種預測模型在D1數據集上的交叉驗證效果整體優于D2，說明當樣本較少時，考慮參與的徑流影響要素越多，效果反而較差。不同預測模型在D1與D2數據集上的10-CV性能對比如表6所示。

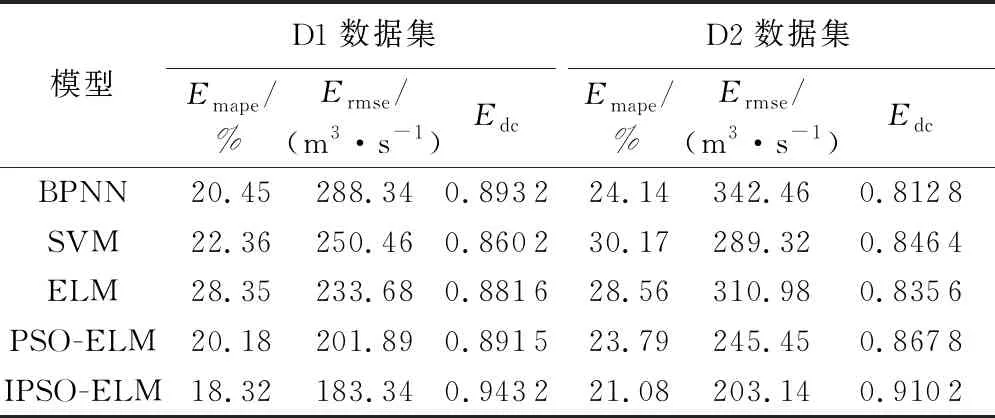
表6 不同模型在D1與D2數據集上10-CV的性能比較

2.4.4預測結果及分析

考慮到模型評測結果的可靠性，在D1與D2數據集上，測試集設計為2006年8月至2008年7月共24組樣本數據，對比模型選用BPNN、SVM、ELM和PSO-ELM。IPSO-ELM模型分別與其他4種模型在D1與D2數據集上的預測結果對比如圖3所示。相對誤差對比曲線如圖4所示，綜合性能對比如表7所示。

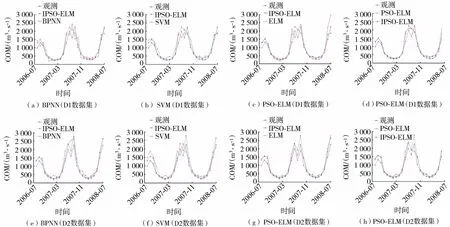
圖3 IPSO-ELM模型與其他4種模型在D1與D2數據集上的預測結果對比

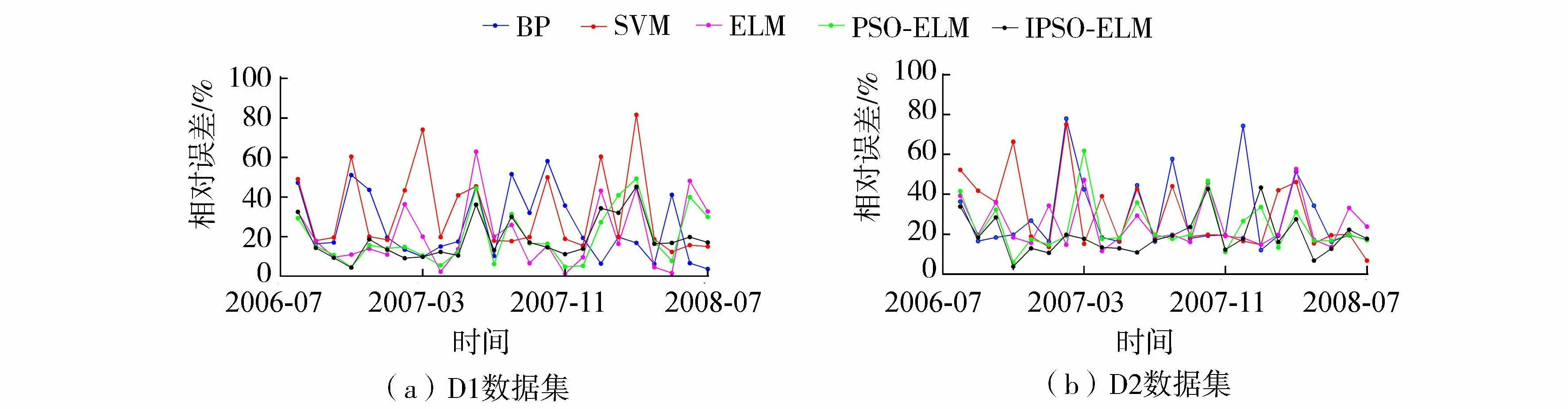
圖4 不同模型在D1與D2數據集上的相對誤差對比曲線

表7 不同模型在D1與D2數據集上的綜合性能對比

2.4.4.1 不同模型預測結果比較

在D1數據集上，5種預測模型均具有較好的預測效果，但在不同的評測指標上展現出具有差異性的結果。其中：在Emape指標上，IPSO-ELM模型最優，相比較，SVM在該項指標上得分較低；Ermse指標與研究區域的年來水量緊密相關，年來水量大的流域，其Ermse指標也較大，其中IPSO-ELM模型的Ermse最小，相比較，BPNN模型較大；在Edc指標上，5種預測模型的確定系數都較高，其中IPSO-ELM模型最優，說明5種預測模型在基于信息熵的因子篩選基礎上對流域中長期徑流預測都具有較好的擬合效果；在Eqr指標上，5種預測模型的合格率都較高，其中IPSO-ELM模型最優(IPSO-ELM為75%，BPNN為62.5%，SVM為58.3%，ELM為66.7%，PSO-ELM為66.7%)，說明5種預測模型均可以應用于水文作業，其中基于IPSO-ELM模型的預報方案屬于乙等，可用于向水文部門正式提供預報成果。

在D2數據集上，5種預測模型均具有較好的預測效果，但在不同的評測指標上展現出具有差異性的結果。其中：在Emape指標上，IPSO-ELM模型最優，相比較，BPNN和SVM在該項指標上得分較低；在Ermse指標上，IPSO-ELM模型最優，相比較，BPNN和SVM的均方根誤差較大；在Edc指標上，IPSO-ELM模型較好，相比較，BP和SVM的確定性系數較低；在Eqr指標上，5種模型的合格率都較高，其中IPSO-ELM模型最優(IPSO-ELM合格率為70.8%，BPNN為62.5%，SVM為58.3%，ELM為62.5%，PSO-ELM為66.7%)。

綜上所述，5種預測模型在D1與D2數據集上均具有較好的預測效果。其中，IPSO-ELM模型的預測效果最佳。主要原因在于：BPNN和SVM模型結構相對復雜，參數在訓練過程中需要初始化與不斷優化調整，整體效率不高，而ELM具有參數設置簡單、計算速度快、誤差小、泛化能力強等優點，因而整體預測效果優于上述兩種常用模型；針對傳統ELM模型輸入權值和隱含層閾值隨機給定，可能導致部分隱含層節點失效問題，本文結合K折交叉驗證與IPSO算法，加快了ELM模型參數尋優速度，因而提高了預測效果。

2.4.4.2 不同數據集上的預測效果比較

在增加徑流影響要素的情況下，5種預測模型在D1數據集上的預測效果整體上勝于D2(增加了NDVI植被指數)，主要原因在于：流域徑流影響要素增多導致模型的輸入變量增加，從而增加了模型的計算復雜度，導致在D2數據集上的整體運算效率不如D1；與中長期徑流預測有關的時間序列較短(訓練樣本較少)，模型難以充分學習，導致D2整體預測效果差于D1。因此，在流域徑流影響要素增多時，模型的輸入維度也相應增加，而時間序列又相對較短(訓練樣本較少)時，預測模型難以充分訓練學習，整體預測效果可能會相對較差。

3 結 論

a.基于各站控制面積的流域徑流綜合指數能夠較好地反映流域水情的豐枯變化。在此基礎上采用基于信息熵的因子篩選方法，獲得了影響流域中長期徑流過程變化的關鍵因子集合，形成IPSO-ELM模型的特征輸入。

b.以K折交叉驗證法求得的均方根誤差作為粒子的適應度，以適應度值為基礎對粒子進行尋優，通過迭代更新找到最優的個體粒子，獲得了ELM模型的最優參數，由此構建了IPSO-ELM模型，并用于流域中長期徑流預測，提高了預測精度。

c.實例計算與對比分析結果表明，所提方法具有較好的實用性，且所建模型性能優于BPNN、SVM、ELM和PSO-ELM等預測模型，可為流域中長期徑流變化趨勢預測分析提供一定參考。