基于數(shù)學(xué)史的圓周率探究活動的設(shè)計與實施

狄邁 余慶純 汪曉勤

【摘 要】一個數(shù)學(xué)主題背后的歷史往往揭示了歷史上數(shù)學(xué)家對該主題的探究過程，為教師設(shè)計探究活動提供了參照。HPM工作室學(xué)員以及來自上海不同學(xué)校的兩位數(shù)學(xué)教師分別設(shè)計了“圓的周長”的教學(xué)。他們都基于數(shù)學(xué)史設(shè)計了圓周率的探究活動，但數(shù)學(xué)史的運(yùn)用方式互不相同，各具特色。

【關(guān)鍵詞】數(shù)學(xué)史;探究活動;圓的周長;圓周率

【作者簡介】狄邁，華東師范大學(xué)教師教育學(xué)院在讀碩士研究生，主要從事數(shù)學(xué)史與數(shù)學(xué)教育研究;余慶純，華東師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院在讀博士研究生，主要從事數(shù)學(xué)史與數(shù)學(xué)教育研究;汪曉勤，華東師范大學(xué)教師教育學(xué)院教授、博士生導(dǎo)師，主要從事數(shù)學(xué)史與數(shù)學(xué)教育研究。

【基金項目】上海高校“立德樹人”人文社會科學(xué)重點研究基地之?dāng)?shù)學(xué)教育教學(xué)研究基地研究項目——數(shù)學(xué)課程與教學(xué)中落實立德樹人根本任務(wù)的研究（A8）

一、引言

荷蘭數(shù)學(xué)家、數(shù)學(xué)教育家弗賴登塔爾（H.Freudenthal）曾指出，數(shù)學(xué)學(xué)習(xí)應(yīng)該是有指導(dǎo)的再創(chuàng)造的過程。要實現(xiàn)“再創(chuàng)造”，教師在課堂上需要設(shè)計探究活動，讓學(xué)生經(jīng)歷知識的發(fā)生、發(fā)展過程或數(shù)學(xué)思想方法的運(yùn)用過程。一個數(shù)學(xué)主題背后的歷史往往揭示了歷史上數(shù)學(xué)家對該主題的探究過程，為教師設(shè)計探究活動提供了參照[1]。當(dāng)代許多西方HPM學(xué)者，如福韋爾（J.Fauvel）、詹克韋斯特（U.Jankvist）等，均指出數(shù)學(xué)史為學(xué)生提供了探究機(jī)會[2]。

《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2011年版）》要求，學(xué)生通過操作，了解圓的周長與直徑之比為定值，掌握圓的周長公式[3]。圓周率作為“圓的周長”主題中的重要內(nèi)容，是引導(dǎo)學(xué)生實現(xiàn)從有限到無限跨越的重要知識載體，因而其教學(xué)一直受到人們的重視。考慮到六年級學(xué)生的認(rèn)知水平，圓周率的探究式教學(xué)不可能完全采用演繹幾何的方式，而只能定位在實驗幾何與演繹幾何之間。

歷史上，古希臘數(shù)學(xué)家安提豐（Antiphon）首次提出用圓內(nèi)接正多邊形面積來逼近圓面積的思想。公元前3世紀(jì)，阿基米德（Archimedes）運(yùn)用同樣的思想，通過依次求出圓內(nèi)接和外切正六邊形、正十二邊形、正二十四邊形、正四十八邊形和正九十六邊形的周長，獲得圓周率的不足和過剩近似分?jǐn)?shù)[4]，即22371<π<227。公元3世紀(jì)，中國數(shù)學(xué)家劉徽利用割圓術(shù)，計算出圓內(nèi)接正一百九十二邊形的面積，得到圓周率的近似值為15750。公元5世紀(jì)，中國魏晉時期數(shù)學(xué)家祖沖之求得圓周率的兩個近似分?jǐn)?shù)，第一個分?jǐn)?shù)稱為“約率”，即阿基米德的227，第二個分?jǐn)?shù)稱為“密率”，即355113，這是祖沖之首創(chuàng)的。據(jù)推測，祖沖之可能是用天文學(xué)家何承天的“調(diào)日法”得到上述兩個分?jǐn)?shù)[5]。

阿基米德和劉徽的正多邊形逼近方法，以及祖沖之的圓周率近似分?jǐn)?shù)求法為來自上海市兩所不同初級中學(xué)的教師A和教師B的教學(xué)設(shè)計提供了參照。基于HPM的視角設(shè)計的“圓的周長”的教學(xué)，教師A擬訂的教學(xué)目標(biāo)如下。

（1）在“觀察—猜想—實驗—?dú)w納—驗證”過程中，探索出圓周長C與直徑d的關(guān)系，歸納圓的周長公式，并學(xué)會運(yùn)用圓的周長公式進(jìn)行簡單計算。

（2）在實驗操作中，體驗“化曲為直”“以直代曲”的數(shù)學(xué)方法;在運(yùn)用“調(diào)日法”計算圓周率的過程中，感悟“無限逼近”的數(shù)學(xué)思想。

（3）在探索過程中增強(qiáng)學(xué)生合作、交流的意識;了解中國古代數(shù)學(xué)家的事跡，增加學(xué)生的文化自信。

教師B擬訂的教學(xué)目標(biāo)如下。

（1）經(jīng)歷操作、歸納與合情推理的過程，探究圓周長與直徑的數(shù)量關(guān)系，得出圓的周長公式，掌握數(shù)學(xué)學(xué)習(xí)過程中“操作—猜想—?dú)w納—推理”的研究方法。

（2）在測量折紙等操作實驗中，感悟與掌握“以直代曲”“無限逼近”的數(shù)學(xué)思想，同時通過幾何畫板等技術(shù)手段的逼近過程，理解圓周率的數(shù)值及其數(shù)學(xué)本質(zhì)。

（3）深刻領(lǐng)會古代數(shù)學(xué)家在求圓周率過程中所運(yùn)用的數(shù)學(xué)思想方法，感受數(shù)學(xué)家堅韌不拔的鉆研精神與一絲不茍的嚴(yán)謹(jǐn)態(tài)度，品味多彩的數(shù)學(xué)文化。

二、教學(xué)過程

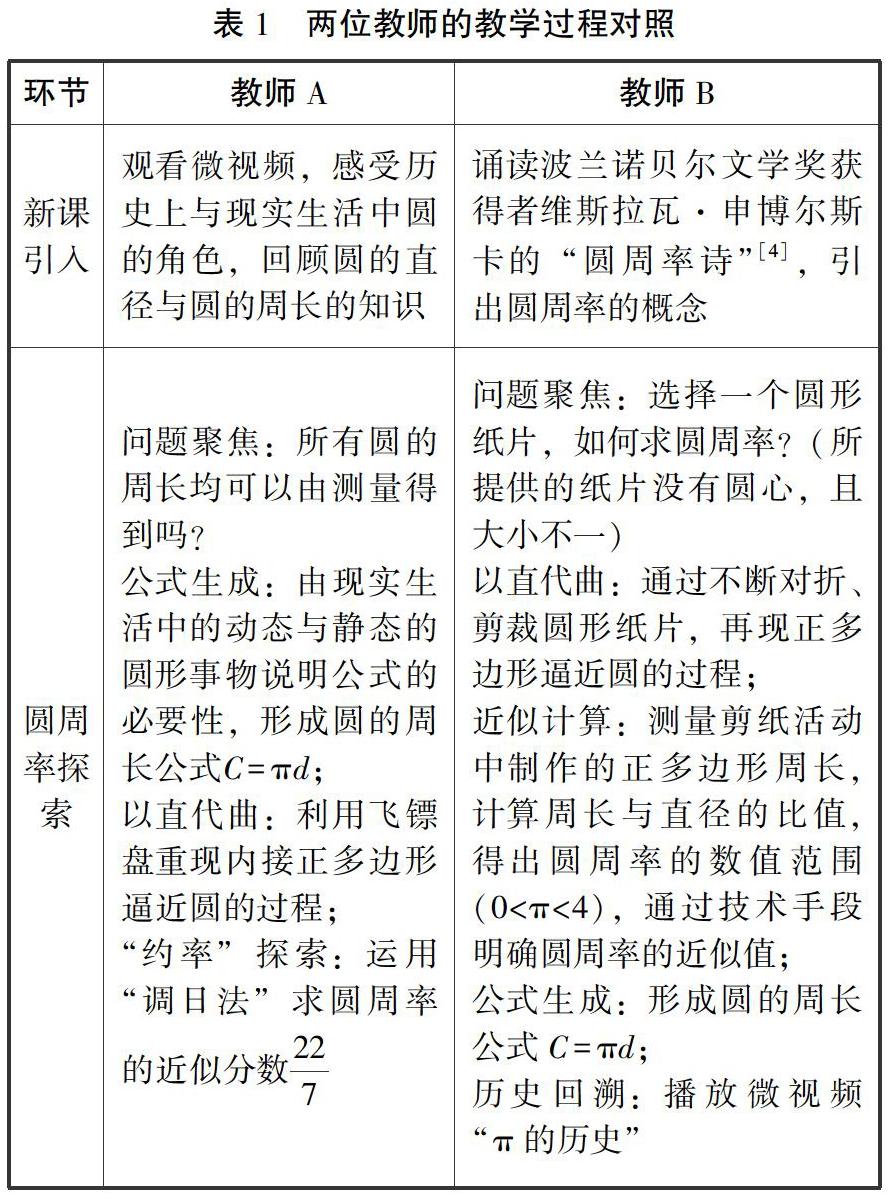
表1概括了教師A和教師B的教學(xué)過程。由表1可知，兩位教師均從數(shù)學(xué)外部引出課題，基于數(shù)學(xué)史，從“正多邊形的逼近”“圓周率近似值的探求”兩方面設(shè)計探究活動。

在“正多邊形的逼近”活動中，教師A由飛鏢盤教具演示，重現(xiàn)阿基米德內(nèi)接正多邊形的窮竭過程，引導(dǎo)學(xué)生體會“無限逼近”與“以直代曲”的數(shù)學(xué)思想;教師B則引導(dǎo)學(xué)生通過不斷對折、剪裁圓形紙片，感受“以直代曲”的思想，進(jìn)一步通過展開紙片，觀察折痕，體會“無限逼近”的數(shù)學(xué)思想方法。

在“圓周率近似值的探求”活動中，教師A引導(dǎo)學(xué)生結(jié)合數(shù)軸，運(yùn)用“調(diào)日法”，由有理數(shù)不斷逼近圓周率，達(dá)成對圓周率這一無理數(shù)的深刻理解;教師B通過測量正多邊形周長，計算其與直徑的比值，得出圓周率的范圍，并通過幾何畫板等技術(shù)手段呈現(xiàn)更精確的數(shù)值，在此過程中讓學(xué)生再次感受“無限逼近”的思想。

三、圓周率探究活動

為更好地進(jìn)行教學(xué)研究，以下是兩位教師圓周率探究活動的教學(xué)片段。

（一）正多邊形的逼近

【教師A的教學(xué)片段1：飛鏢盤模型】

師：古希臘數(shù)學(xué)家阿基米德通過“窮竭法”，運(yùn)用“無限逼近”的思想得出了圓周率的近似值，他是怎么做的呢？老師通過飛鏢盤給大家簡單演示一下。首先，在直徑為2的圓周上選取六個點，將圓周六等分，連接各個點得到一個正六邊形。此時正六邊形的周長等于6。現(xiàn)在這個正六邊形的周長與其直徑的比值是多少？

生：3。

師：它能代替圓周率的值嗎？

生：不能。

師：為什么？

生：差得太多了。

師：沒錯。阿基米德也覺得這樣不行，于是他又繼續(xù)分割，這樣能夠得到正幾邊形？（如圖1）

生：正十二邊形。

師：這樣求出的比值會怎么樣？

生：更接近圓周率的值。

師：是的。但是阿基米德還是不滿意，就繼續(xù)分割成正二十四邊形，正四十八邊形……這體現(xiàn)了什么思想？

生：體現(xiàn)了“無限逼近”的思想。

【教師B的教學(xué)片段1：剪紙】

師：請同學(xué)們拿出課前發(fā)的圓形紙片，通過不斷對折、剪裁，得到一個正多邊形[HTSS]（教師示范對折兩次紙片并加以剪裁的效果，如圖2）。

師：請問得到的是什么圖形呢？

生：正方形。

師：很好。接下來請同學(xué)們增加對折的次數(shù)，并加以剪裁，看看能得到什么圖形？

生：對折三次，得到了正八邊形，四次后得到正十六邊形……

師：（在黑板上展示學(xué)生探究所得的不同形狀的紙片）請仔細(xì)觀察，隨著對折次數(shù)的增加，你能發(fā)現(xiàn)什么規(guī)律？

生：對折次數(shù)越多，剪裁后的紙片就越像圓。

師：沒錯。因為操作折紙的對折次數(shù)是有限的，下面通過幾何畫板演示，觀察一下當(dāng)對折次數(shù)逐漸增加時，所裁剪的正多邊形的變化。

師：當(dāng)正多邊形的邊數(shù)無限增加時，還能看到正多邊形嗎？

生：看不到了。

師：不錯。當(dāng)圓的內(nèi)接正多邊形的邊數(shù)無限增加時，可以看到正多邊形的周長無限趨近于圓的周長，此時圓的周長即近似為正無限邊形的周長。用多邊形的每一條邊近似取代它們所對的弧，在數(shù)學(xué)上我們把這種思想叫作“以直代曲”。

（二）圓周率近似值的探求

【教師A的教學(xué)片段2：“調(diào)日法”】

師：我國著名數(shù)學(xué)家祖沖之將圓周率的值計算到了在3.1415926與3.1415927之間，但是他的偉大不僅僅局限于進(jìn)一步計算出圓周率的近似值，而是發(fā)現(xiàn)了用圓周率的小數(shù)形式計算圓的周長很麻煩，于是通過探索發(fā)現(xiàn)了“約率”227與“密率”355113，他是如何探索出來的呢？

師：其實該方法現(xiàn)在還在使用，這就是“調(diào)日法”（教師介紹“調(diào)日法”的計算，考慮用“調(diào)日法”逼近π。）。

師：為什么一開始的范圍是31<π<41？

生：π的取值在3和4之間。

師：是的。實際上古人是從幾何方面來看的。當(dāng)在圓內(nèi)接正六邊形時，根據(jù)其周長與直徑關(guān)系，得到圓周率π大于3;當(dāng)外切正方形時，得到圓周率π小于4。請問誰來介紹一下41<72<31是如何探究出來的？（如圖3）

生1：將31與41的分母與分子分別相加，得到41<72<31。

師：很好。那么數(shù)軸上41與72哪個數(shù)更逼近π？

生：72。

師：根據(jù)數(shù)軸的“逼近”，應(yīng)該舍棄哪個數(shù)呢？

生：舍棄41。

師：很好，下面我們繼續(xù)探究。

【教師B的教學(xué)片段2：測量與幾何畫板】

師：通過剛剛的探索，知道當(dāng)圓內(nèi)接正多邊形邊數(shù)無限增加時，正無限多邊形的周長便是圓的周長。由此，可以通過正多邊形與直徑的比值來求解圓周率的值嗎？

生：可以。

師：下面請同學(xué)們測量手中圓形紙片內(nèi)接正方形、正八邊形與正十二邊形的周長，計算它們與圓直徑之間的比值，并請每個小組分享一下你們的發(fā)現(xiàn)。

生：計算出來的多邊形周長與直徑的比值與3.14相差比較大。

師：為什么？

生1：因為在測量過程中存在一定的誤差。

生2：但是計算的數(shù)值是介于3與4之間。

師：是的。由于測量誤差，計算得出的圓周長與直徑的比值與3.14有一定的距離，但是它們均介于3與4之間。接下來，通過幾何畫板客觀精確地感受當(dāng)正多邊形邊數(shù)增加時，其周長與直徑比值之間的關(guān)系。（如圖4）

師：大家觀察到了什么？

生：當(dāng)圓的內(nèi)接正多邊形邊數(shù)無限增加時，其周長與直徑的比值越接近圓周率的實際值。

師：實際上，在公元前3世紀(jì)，古希臘數(shù)學(xué)家阿基米德利用“窮竭法”使內(nèi)接正多邊形與外切正多邊形共同逼近，推求圓的周長進(jìn)而得到圓周率π的近似值。其通過圓的內(nèi)接與外切正多邊形，當(dāng)正多邊形的邊數(shù)n無限增加時，兩個正多邊形的周長都會無限接近圓的周長，以此探求圓的周長與圓周率的值。（如圖5）

四、圓周率探究活動評析

由以上分析可知，兩位教師均解析了圓周率的相關(guān)歷史，提煉其發(fā)展過程中的重要思想，并基于此設(shè)計數(shù)學(xué)探究活動。現(xiàn)對教師A和教師B在兩個數(shù)學(xué)探究活動中所運(yùn)用的數(shù)學(xué)史及其方式進(jìn)行分析（見表2）。

教師A順應(yīng)式地運(yùn)用阿基米德的“窮竭法”，以飛鏢盤模擬圓內(nèi)接正多邊形的分割過程，重現(xiàn)“無限逼近”“以直代曲”的數(shù)學(xué)思想方法;同時，順應(yīng)式地運(yùn)用何承天的“調(diào)日法”，引導(dǎo)學(xué)生用有理數(shù)逼近圓周率，促進(jìn)對π這一無理數(shù)的深入了解。在此過程中，教師A忽略了阿基米德“窮竭法”的外切正多邊形這一方面，使該方法在課堂上沒有完整地呈現(xiàn)。由此可見，教師A基于圓周率發(fā)展史上兩個重要階段——阿基米德“窮竭法”的幾何逼近與何承天“調(diào)日法”的數(shù)值逼近，順應(yīng)式地設(shè)計了相應(yīng)的探究活動，引導(dǎo)學(xué)生完成對圓周率由幾何和數(shù)值兩方面的逼近，滲透“無限逼近”的數(shù)學(xué)思想，達(dá)成了本節(jié)課的教學(xué)目標(biāo)。

對于課后學(xué)習(xí)單中問題“通過這節(jié)課的學(xué)習(xí)，你能否解釋‘地球是圓的，但是我們感覺自己是行走在平地上，而不是球面上的現(xiàn)象”，大多學(xué)生這樣解釋：由于地球太大了，因此我們行走的弧可以看成直線。這反映出學(xué)生對“無限逼近”與“以直代曲”思想的深刻理解，能夠運(yùn)用掌握的數(shù)學(xué)知識解釋現(xiàn)實現(xiàn)象，解決實際問題，這也從側(cè)面反映出教學(xué)目標(biāo)的達(dá)成。

另一方面，教師B借鑒阿基米德“窮竭法”，運(yùn)用順應(yīng)式，將兩個探究活動有機(jī)地連接在一起，進(jìn)而滲透“無限逼近”的思想。第一階段的剪紙活動引導(dǎo)學(xué)生自己動手操作，在剪裁過程中體會“以直代曲”思想，通過制作的正多邊形與圓的比較，感受“無限逼近”的過程與思想，在操作與思維的交互過程中與古人對話;第二階段通過測量與計算，得到圓周率的范圍在3～4之間，學(xué)生在得到與自己心目中相差甚遠(yuǎn)的答案時實事求是，體現(xiàn)了數(shù)學(xué)研究過程中的求真意識，達(dá)成德育之效[6]。借助幾何畫板呈現(xiàn)數(shù)值，使學(xué)生在幾何與數(shù)值方面體會了“無限逼近”的過程。

在課后的反饋中，部分學(xué)生對由“無限逼近”得到的錯誤結(jié)論“π=4”的原因進(jìn)行了思考與闡述。可見，通過探究活動，教師B的學(xué)生對“無限逼近”與“以直代曲”有了新的思考，并能對其進(jìn)行拓展與延伸，達(dá)成了教師B提出的“感悟與掌握‘以直代曲‘無限逼近的數(shù)學(xué)思想”的教學(xué)目標(biāo)。

綜上所述，兩位教師均基于圓周率發(fā)展的“幾何逼近”與“數(shù)值逼近”兩個方面，開展教學(xué)實踐;但從融入的方式來看，兩位教師均采用了順應(yīng)式而非重構(gòu)式，即將歷史上探究圓周率的方法作為參照設(shè)計探究活動，進(jìn)行古今對照。

五、教學(xué)啟示

對兩位教師設(shè)計的基于數(shù)學(xué)史的圓周率探究活動進(jìn)行分析，可為今后HPM視角下探究式教學(xué)提供以下啟示。

（1）加強(qiáng)歷史研究，提升專業(yè)知識。由上文可知，兩位教師均未采用重構(gòu)的方法融入數(shù)學(xué)史，且在圓周率的探究活動上缺乏基本的發(fā)生動因。究其原因是由于教師對圓周率的歷史發(fā)展并未深入了解，也未將其作為參照來開展探究性教學(xué)。因此，一線教師要加強(qiáng)歷史研究，解析數(shù)學(xué)史料，提升數(shù)學(xué)專業(yè)知識;同時基于教學(xué)實踐，提升教學(xué)內(nèi)容，促進(jìn)數(shù)學(xué)史自然地融入數(shù)學(xué)教學(xué)。

（2）融入信息技術(shù)，優(yōu)化數(shù)學(xué)教學(xué)。在教師B的課堂中，通過對制作的正多邊形的周長進(jìn)行測量，對周長與直徑的比值進(jìn)行計算，得出圓周率的范圍，之后再通過幾何畫板的演示，讓學(xué)生更加精確地感受圓周率的數(shù)值，并在此逼近過程中滲透“無限逼近”與“以直代曲”的思想，引導(dǎo)學(xué)生感受知識源流，品味古今數(shù)學(xué)文化，達(dá)成相應(yīng)的教學(xué)目標(biāo)。

參考文獻(xiàn)：

[1]弗賴登塔爾.作為教育任務(wù)的數(shù)學(xué)[M].陳昌平，唐瑞芬，等，譯.上海：上海教育出版社，1995.

[2]汪曉勤.HPM：數(shù)學(xué)史與數(shù)學(xué)教育[M].北京：科學(xué)出版社，2017.

[3]中華人民共和國教育部.義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2011年版）[M].北京：北京師范大學(xué)出版社，2012.

[4]汪曉勤，趙紅琴.阿基米德與圓周率[J].數(shù)學(xué)教學(xué)，2004（1）：40-41，39.

[5]曲安京.祖沖之是如何得到圓周率π=355/113的？[J].自然辯證法通訊，2002（3）：72-77，96.

[6]張冰，蔡春夢，雷沛瑤.HPM視角下的指數(shù)函數(shù)概念教學(xué)設(shè)計研究[J].中小學(xué)課堂教學(xué)研究，2021（6）：5-10.

（責(zé)任編輯：陸順演）