面向深度調峰的火電機組靈活性改造規劃模型

楊寅平，曾 沅，秦 超，王成山

（智能電網教育部重點實驗室（天津大學），天津市 300072）

0 引言

可再生能源大規模接入電網，對電網調峰能力提出了更高的要求。以中國現有的電源結構，無論裝機容量還是發電量都是以火電為主，故利用火電機組進行深度調峰仍是當前電網的主要選擇［1-2］。在火電機組參與深度調峰時，需要提前進行靈活性改造以降低機組的最低出力極限。文獻［3］構建了適用于大規模風電接入場景下的火電機組靈活性改造規劃模型，在優化目標中計及了改造、發電和棄風成本，并采用Benders分解法實現了模型的高效求解。文獻［4-5］從技術角度分析了影響火電機組調峰能力的主要因素，提出了火電機組在各調峰階段中的能耗成本模型，并詳細分析了火電機組在不同調峰深度下對系統產生的影響。目前，研究工作仍集中于火電機組在實施不同靈活性改造方案下的系統經濟性分析，網絡拓撲結構對靈活性改造規劃所造成的影響以及方案在多個場景下的適應性等仍有待進一步深化研究。

綜上，結合火電機組在深度調峰階段的運行特性，本文提出了一種基于區間整體優化［6-9］的火電機組靈活性改造規劃模型，該模型具有如下特性。

1）在模型中引入了火電機組在深度調峰不同階段運行中的詳細成本模型，包含了顯性的燃料費用和用于穩定鍋爐燃燒的柴油費用，以及隱性的機組損耗費用［4-5］。因此，所構建的成本模型更加貼近實際運行中的經濟特性。

2）火電機組運行在深度調峰階段中的單位發電成本大幅上升，選擇以非投油調峰方式和投油調峰方式來消納風電，或者選擇棄風均會對系統運行費用產生較大影響。針對這一問題，在模型中引入了區間優化方法，以結合多個場景運行費用以及機組改造費用的年綜合費用區間作為優化目標，并使用2個步驟來實現求解。首先，使用多領頭群優化（group search optimizer with multiple producers，GSOMP）算法［10-12］來協同優化目標區間的2個特征量，得到多個具有不同目標區間特性的候選方案。其次，使用多屬性決策（multiple attributeddecision making，MADA）方法［13-14］對各個候選方案的目標區間進行綜合評估，從而得到一組綜合經濟性最優的方案。

3）需要火電機組進行深度調峰的電網往往接入了高比例風電，這些風電的高不確定性極易造成各運行場景下的潮流阻塞，尤其在風電極限送出場景下。所提出的模型以區間優化方法實現了全場景優化，特別考慮了各風電極限送出場景下的潮流優化，從而提高了模型所提供方案的潮流適應性，有效減少了各場景下由于潮流阻塞所造成的棄風量。

1 火電機組靈活性改造規劃模型的建立

1.1 火電機組調峰成本模型

依據不同的調節能力和成本特性，火電機組的運行過程可以分為常規調峰（regular peak regulation，RPR）、非投油調峰（deep peak regulation without oil，DPR）、投油調峰（deep peak regulation with oil，DPRO）3個階段。如圖1所示［4-5，15］，Pa、Pb、Pc、Pmax分別為機組在RPR、DPR和DPRO階段的最小技術出力以及最大出力。

圖1 火電機組調峰過程示意圖Fig.1 Schematic diagram of peak regulation process of thermal power units

在RPR階段，火電機組的運行成本僅包含煤耗費用，該費用通常基于煤耗特性函數f(·)進行計算，如式（1）所示。

式中：a、b、c分別為機組耗量特性函數的二次項、一次項、常數項系數，其取值與機組類型、鍋爐型號和煤質有關；Scoal為當季的單位煤炭價格；P為機組有功出力。

在DPR和DPRO階段，深度壓低機組出力會造成轉子軸系熱應力過大，引起轉子低周疲勞損耗和蠕變損耗，進而導致機組本體發生嚴重的變形和斷裂，縮短機組壽命。汽輪機轉子壽命的計算是一個非常復雜的問題，現有研究中尚無公認的計算公式可以有效解決。本文將按照轉子材料的低周疲勞特性關系進行低周疲勞壽命損耗計算。

Manson-coffin公式體現了總應變幅度與轉子致裂循環周次的關系，其函數關系為：

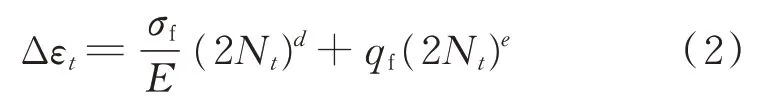
式中：σf為材料的疲勞強度系數；qf為材料的疲勞延性系數；d為材料的疲勞強度指數；e為材料的疲勞延性指數；Nt為時刻t轉子致裂循環周次，與機組出力P有 關；Δεt為 時 刻t轉 子 總 應 變 幅 度；E為 彈 性模量。

根據機組轉子的應力及離心切向應力可得到轉子的總應變幅度Δεt，代入式（2）可以確定轉子致裂循環周次Nt，再結合機組購機成本可粗略得到機組的損耗費用wcost(P)為：

式中：Sunit為機組購機成本。

在DPRO階段，鍋爐的燃燒穩定性、水動力工況安全性都迅速下降，會出現無法穩定燃燒的情況，機組需要投油助燃以保證機組的安全運行，投油費用woil為：

式中：Scost為機組當季燃油價格；Zoil為機組投油量。

綜上，火電機組在不同調峰階段中的運行成本具有不同的特性，詳細的火電機組運行成本可以表述為如下的分段函數：

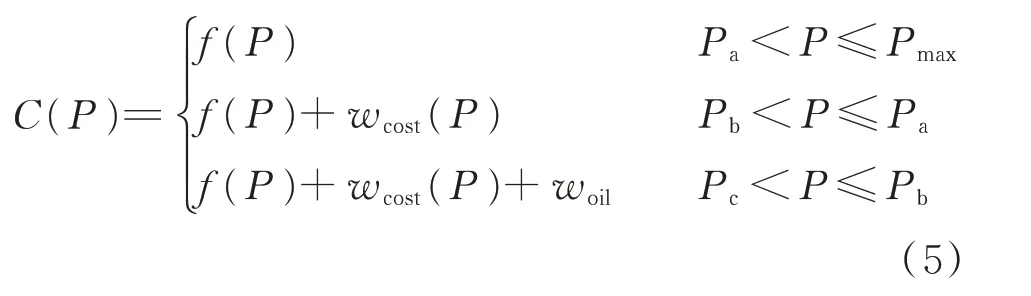
式中：C（P）為火電機組的運行成本。

式（5）中f(P)和woil均屬于顯性成本；wcost(P)屬于隱性成本。

1.2 火電機組靈活性改造規劃確定性模型

所建立的火電機組靈活性改造規劃確定性模型，綜合考慮了火電機組的靈活性改造費用以及改造后的運行費用。為了便于長期規劃及運行中計算周期的統一，將模型的優化周期選擇為1年，即以年化改造費用和年運行費用的年綜合費用作為模型的優化目標。該模型具體表述如下。

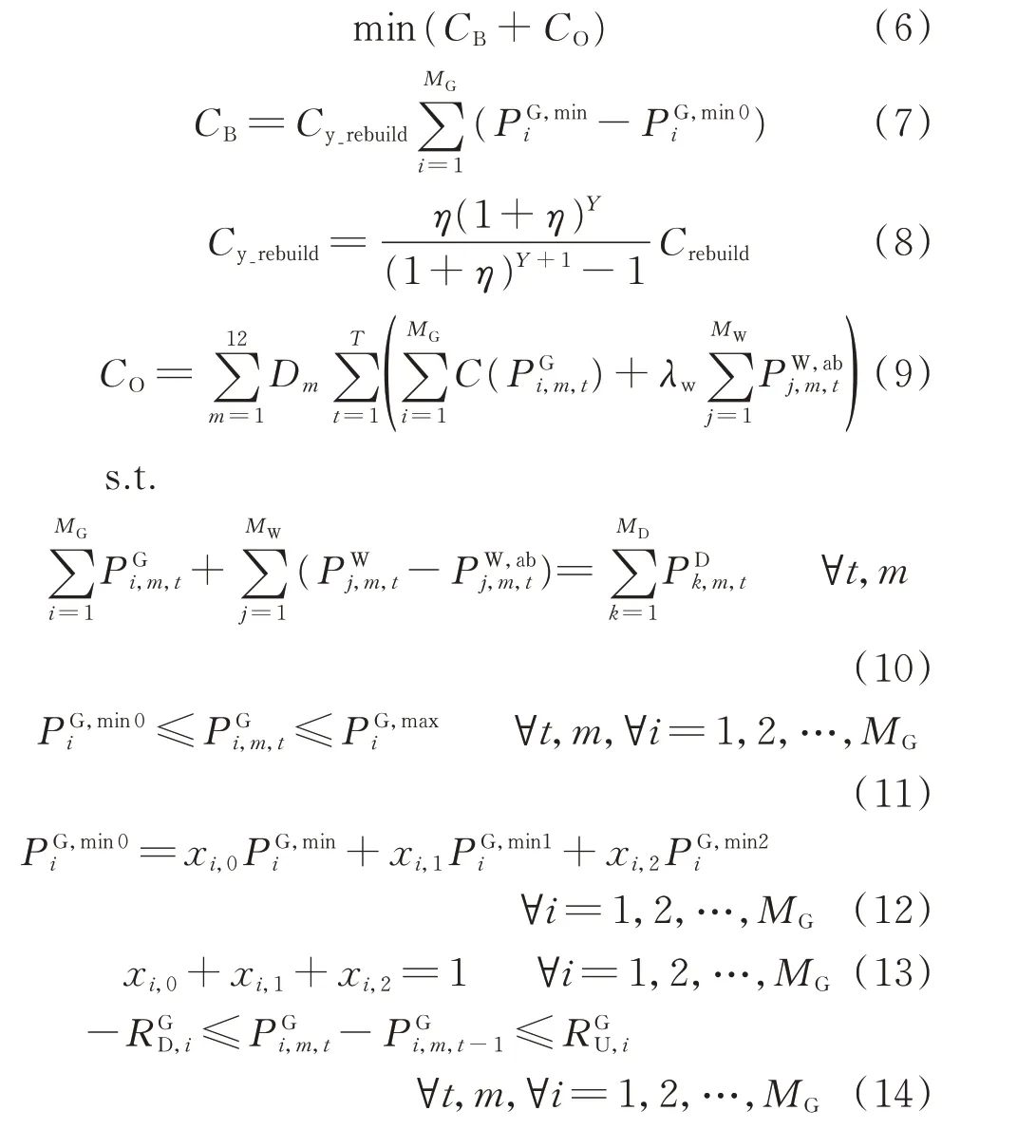
式（6）表示模型的優化目標為最小化年綜合費用，包括了年化改造費用和年運行費用。式（7）給出了火電機組年化改造費用的公式。式（8）給出了單位容量的年改造費用的折算公式。式（9）給出了系統中年運行費用的公式。式（10）為系統中的功率平衡約束。式（11）為火電機組的出力約束。式（12）和式（13）為火電機組的靈活性改造約束。式（14）為火電機組的爬坡約束。式（15）為線路潮流約束。式（16）為風電機組的棄風量約束。

該模型可以表示為如下的通用形式：

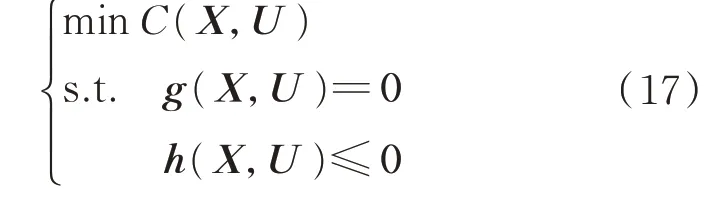
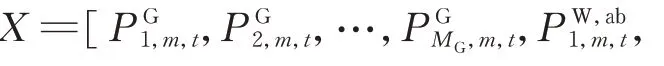
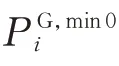
1.3 火電機組靈活性改造規劃區間模型

較之傳統的火電機組，風電機組的出力具有較強的波動性，這導致實際計算中風電的出力存在較高的不確定性。當多個風電場在各時段出力范圍區間內波動時，將產生多個不確定場景，不確定場景s可表示為：

從給出的場景s表達式Ps，m中可以看出，考慮到多個風電場的波動性后，會衍生出大量的不確定場景。在系統中存在大量不確定場景的情況下，區間方法通過限定各個節點不確定場景的波動范圍，進而限定場景集的邊界，邊界范圍內可以覆蓋所有過渡場景中的值。所提出的模型旨在尋找一組火電機組靈活性改造方案，使之能夠滿足在多個運行日中風電波動范圍內電網潮流可行并具有最優的經濟性。

原模型中的式（9）—式（11）、式（14）—式（16）可以轉換為區間形式，其表述形式以及相應的場景削減方法如下。

1）系統運行費用

年運行費用區間的上、下限分別如式（20）和式（21）所示。

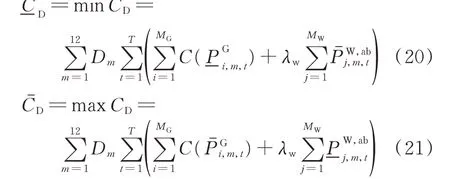
2）功率平衡等式

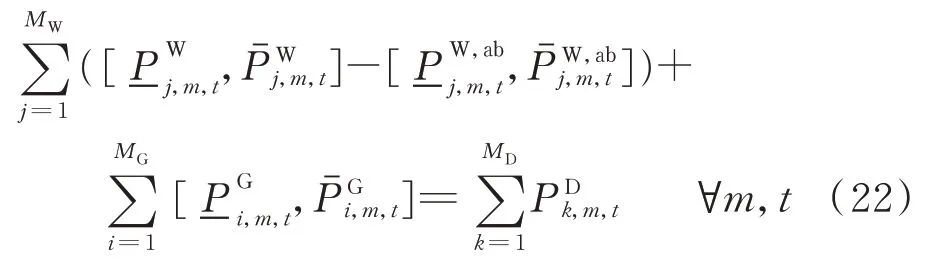
系統中的功率平衡等式由4個部分構成，分別為火電機組出力、風電機組出力、負荷以及棄風量。由于風電機組出力及負荷功率都是一個已知量，故可將該已知量轉移至等式的等號右側，從而反映未知量的出力范圍。

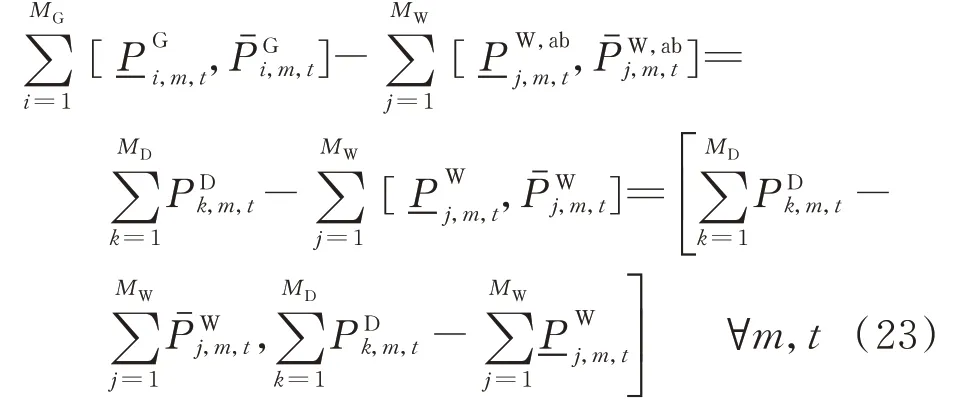
將式（23）等號左側2個區間的上限值和下限值分別進行結合，可以得到2個極限場景，該區間等式可以轉換為如下2個極限場景下的功率平衡等式。

依據區間不等式的上限、下限嚴格約束，可以將式（26）轉換為以下2個不等式。

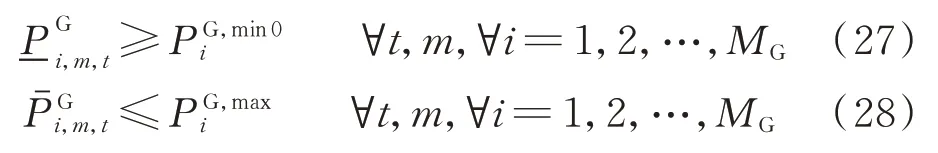
4）爬坡約束

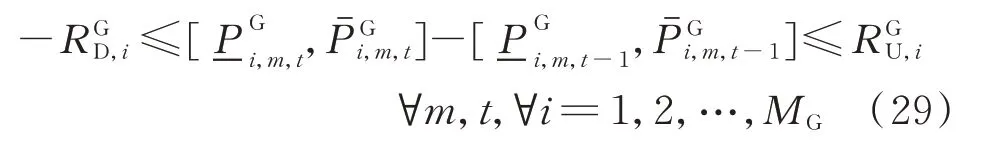
通過對這2個區間的上限、下限進行約束，可以將式（29）轉換為以下2個不等式。

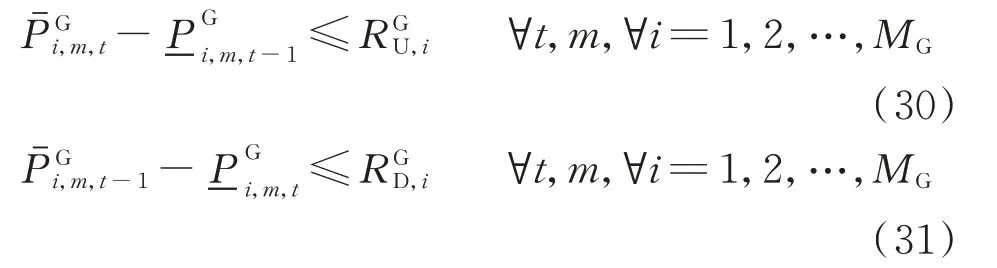
5）線路潮流約束

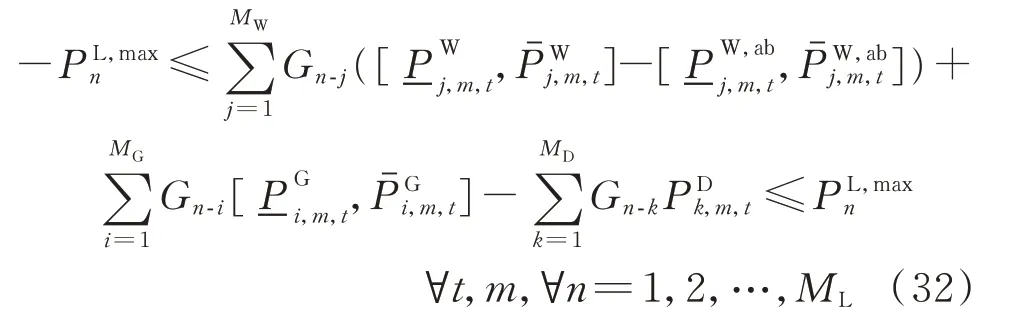
將該區間不等式的已知量與未知量分別轉移至不等式的兩側，并將該雙側不等式轉換為2個單側不等式以便于求解，可得：

對于等式右側的已知量，依據低邊界理論對區間邊界進行縮緊，選擇不等式右側的最小量作為邊界的縮緊條件，該條件為加于線路潮流中的最緊約束，可以保證所有可能場景下的潮流可行。對于等式左側的未知量，依據區間的上限、下限進行約束。通過上述過程，可以將2個不等式轉換如下。

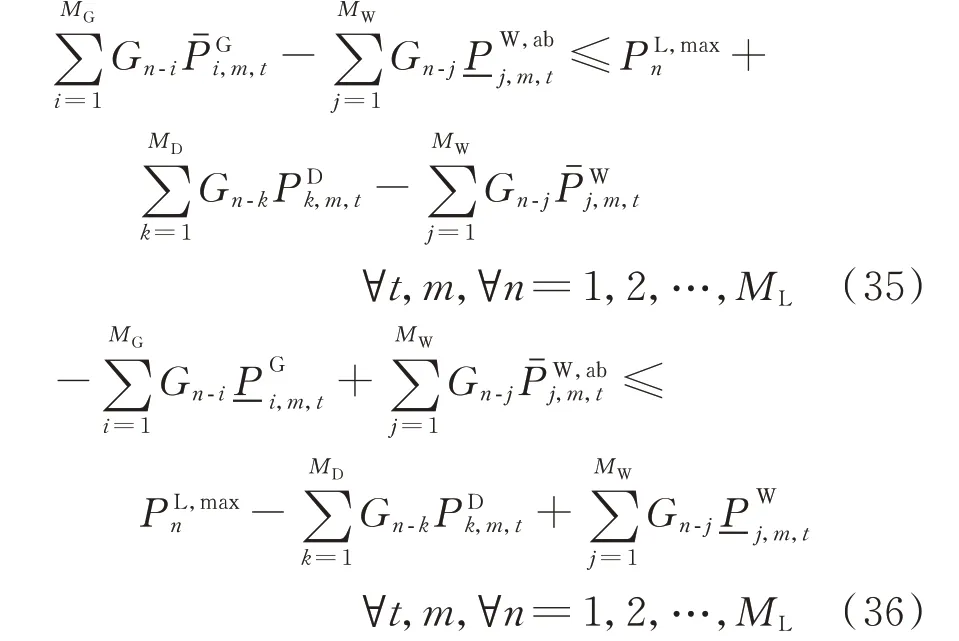
6）棄風約束

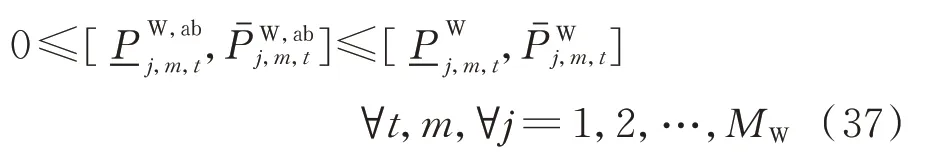
對于該區間不等式，只要對2個區間的上、下限分別進行約束即可保證所有場景均可滿足要求。該不等式可轉換為以下2個約束。

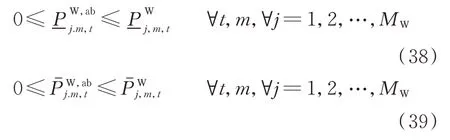
綜上所述，原有模型中的約束條件以及目標函數可以由區間形式來表述，并可以通過嚴謹的數學推導來進行全場景削減，確保各區間范圍覆蓋了所有可能的過渡場景。原模型可以表述為如下的通用形式：

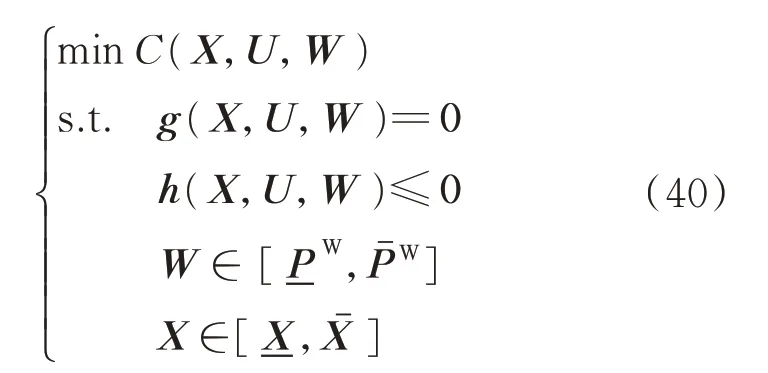
所提出模型的優化目標中共包含2個部分，一部分是火電機組的年化靈活性改造費用，是一個單值目標；另一部分是在給定風電出力預測區間下形成的年運行費用區間，是一個區間目標。為了便于計算，合并這2個部分的費用得到年綜合費用區間。為了綜合衡量目標區間的整體特性，使用區間均值和偏差值作為區間的特征量來進行協同優化。原模型可以轉換為［9，11，16］：

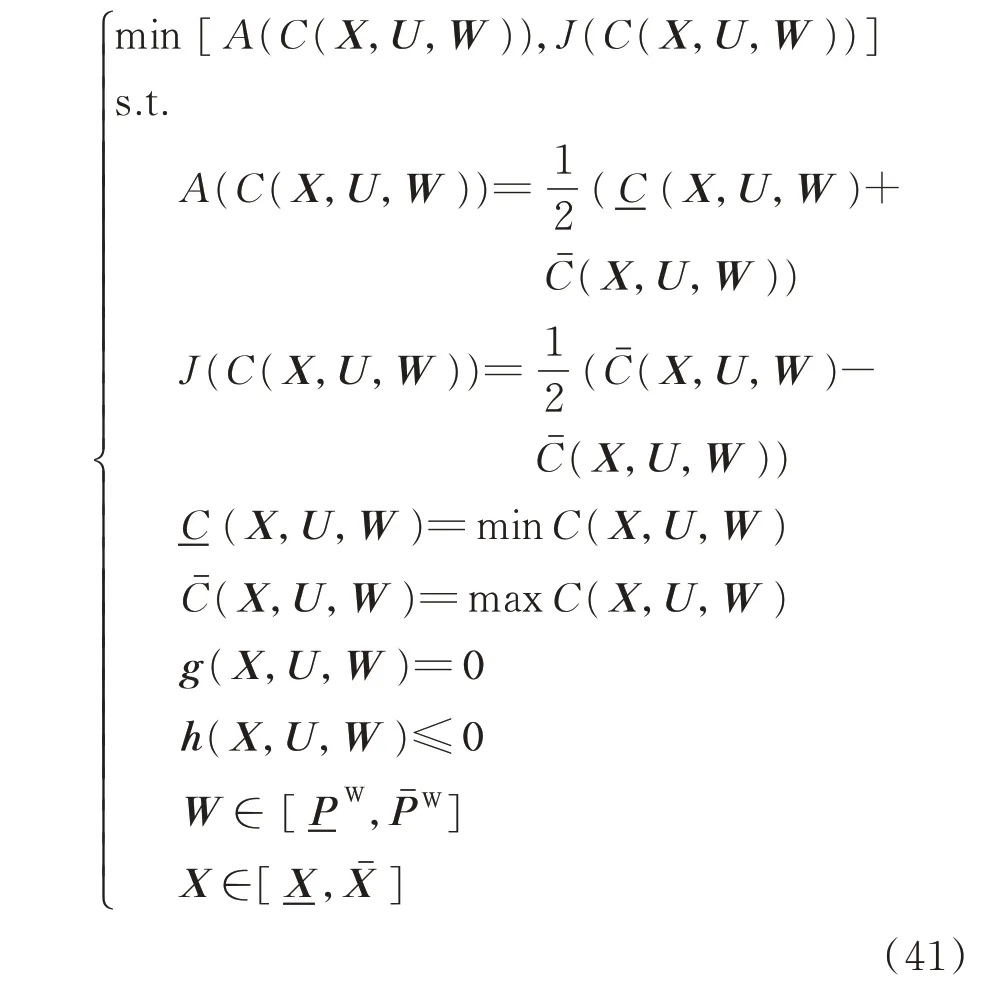
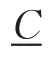
2 火電機組靈活性改造模型求解方法

本文中將所提出的火電機組靈活性改造模型轉換為一個多目標優化問題。多目標優化本質上是一個兩階段優化問題，包含多目標尋優和多目標決策2個階段。在該模型的求解中，首先，使用GSOMP算法對所提出的模型進行多目標尋優，求解得到一組最優的非支配解集。其次，使用證據推理方法對解集內的每個解進行綜合評估，依據用戶的需求從解集中選擇一個最優解。

2.1 基于GSOMP算法的區間優化模型求解方法

GSOMP算法［11-12］是一種基于群體搜索的多目標優化方法。該方法在尋優過程中模擬了蜂群智能搜索技術，因而在搜索非支配解集的應用中具有良好的表現。本文采用GSOMP算法求取一組側重于不同子目標的非支配最優解集（帕累托解集），具體的計算流程如圖2所示。圖2中K和Kmax分別為迭代次數和最大迭代次數。

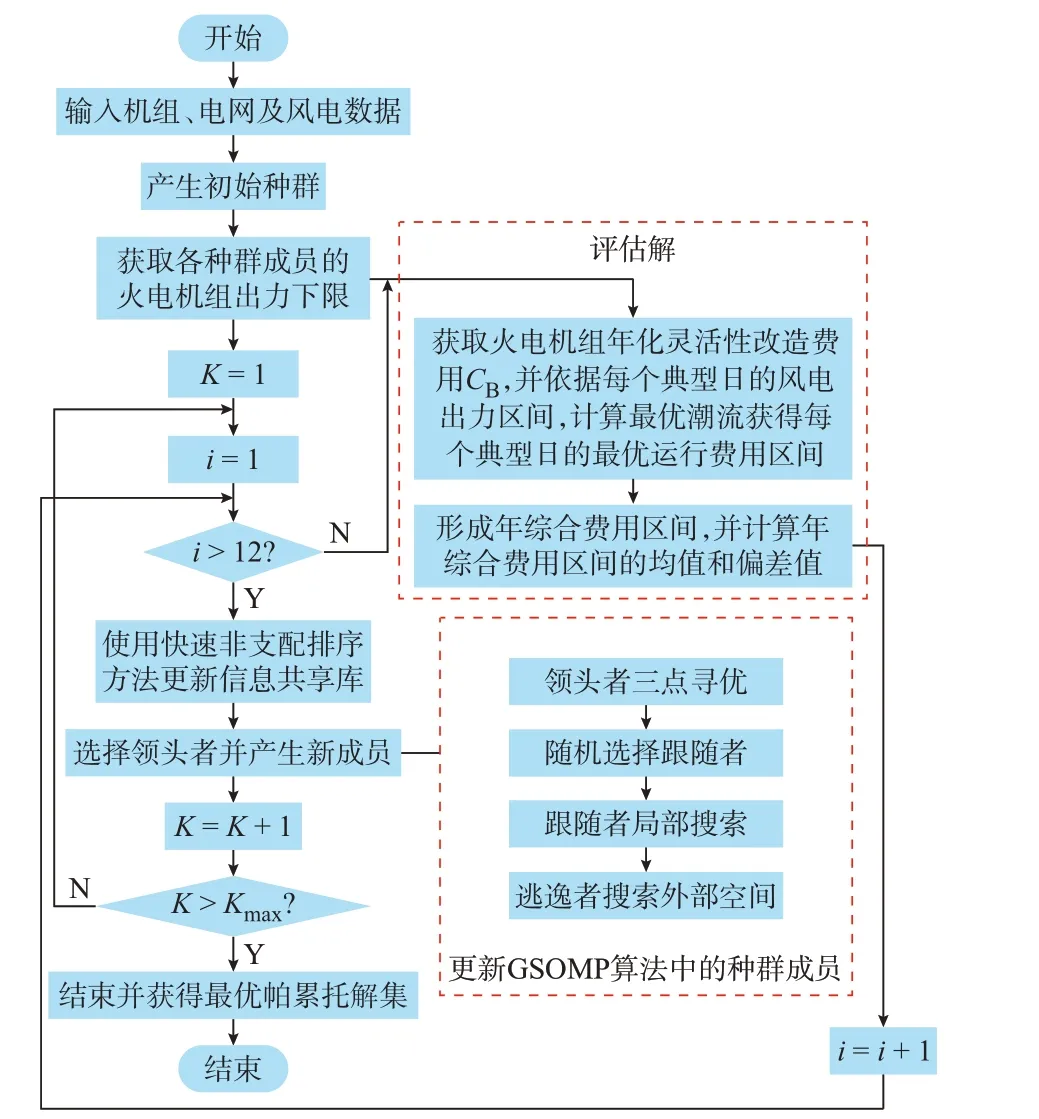
圖2 采用GSOMP算法求解模型的流程圖Fig.2 Flow chart of model solved by GSOMP algorithm

2.2 基于證據推理的目標區間評估方法

采用GSOMP算法對所提出的模型進行多目標尋優可以獲取一組非支配解集，該解集中包含了多個具有不同年綜合費用區間特性的候選方案。本節采用證據推理方法對多個優化子目標進行綜合評估，從多個候選方案中選擇最優方案。

證據推理方法是一種基于屬性的三層啟發式評估方法［13-14］，整體結構如附錄A圖A1所示。在評估框架的底層，定義了各待評估的基本屬性Ii（i=1，2），每個基本屬性具有一個相應的權重值αi（i=1，2），該模型中的基本屬性即為年綜合費用區間的均值和偏差值。在評估框架的中間層，共設置了5個評價等級Hn（n=1，2，3，4，5），分別為優秀、良好、一般、勉強和差。該層將各個基本屬性劃分至5個評價等級中并生成相應的等級置信度βn，i，通過結合各個基本屬性的等級評估結果以及權重值，可以得到各方案在5個評價等級上的綜合評估結果。在評估框架的頂層，將各個等級的評估結果以及相應的等級需求程度進行結合，就得到了方案的綜合評估結果。

依據上述步驟對每個候選方案進行評估，并對評估結果進行依次排序即可得到一組最優方案，具體的評估方法如文獻［9］所述。

3 算例分析

3.1 基礎算例

本文以修改后的IEEE 39節點系統［17］為例，驗證所提出的火電機組靈活性改造規劃模型及其求解方法的有效性。該算例系統包含10臺火電機組，裝機容量共計6 512 MW；系統中擁有17個負荷節點，各節點負荷共計6 147 MW。該系統在節點28、30、37、38分別接入了1個風電場，容量均為700 MW。火電機組參數詳見附錄A表A1，機組的運行參數采用算例原始數據，機組的煤耗數據來自實際電網中的火電廠數據，煤炭價格和投油所用的柴油價格分別為550元/t以及6 130元/t，購機費用為火電廠的實際建設費用［1］。節點負荷數據詳見附錄A表A2，各月典型日的負荷數據來自實際電網，負荷在各時段的值則依據各節點的原始負荷情況按比例進行增減。風電場的出力采用某電網中的實際風電場出力，風電場出力的預測誤差設置為20%，棄風懲罰費用為500元/（MW·h）［18］。火電機組損耗參數［15］見附錄A表A3，該表顯示了火電機組在不同調峰深度下的機組損耗情況。

火電機組在實施靈活性改造前的調峰容量為額定容量的50%［19］。按照不同的調節能力可將火電機組的靈活性改造方案分為2種，分別為非投油調峰改造方案和投油調峰改造方案，改造后的機組最低出力分別為額定容量的35%和20%。火電機組的靈活性改造費用為105萬元/MW［20］，按照改造后機組繼續運行20年、年利率6%進行折算，年化靈活性改造費用為8.8萬元/MW。在模型的求解中，設置GSOMP算法中的最大迭代次數為60次，每次迭代中存儲5個最優解，附錄A圖A2中給出了不同迭代次數下的最優非支配解集，以驗證所設置的迭代次數可以保證足夠的計算精度。在評估階段設置了5個評價等級，分別為{優秀、良好、一般、勉強、差}，各個評價等級的劃分標準表述如下：依次排序各個候選方案中的年綜合費用區間和偏差值，選擇最優值為優秀等級的評價標準，選擇最差值為差等級的評價標準，其他等級的評價標準則依據最優值和最差值之間的偏差均分得到。各個評價等級所設置的效用值分別為{1.00，0.85，0.55，0.35，0}［13］。

3.2 基礎算例仿真結果

在MATLAB軟件中搭建所提出的模型，使用CPLEX求解器進行求解。所提出的模型以包含火電機組年化改造費用和多個不確定場景下運行費用的年綜合費用區間作為優化目標。當協同優化目標區間的均值和偏差值時，可以獲取6個非支配最優解，每個解代表一組火電機組靈活性改造方案，分別為方案A1、A2、A3、A4、A5、A6。

如圖3所示，以所獲取的6個候選方案A1至A6實施火電機組靈活性改造時，各組方案所形成的年綜合費用區間呈現出不同的區間特性。方案A1具有最低的區間均值，方案A6具有最小的區間偏差值。從方案A1到A6，各方案中的區間偏差值持續降低，而區間均值則有所升高。年綜合費用區間的均值和偏差值作為模型中的2個優化子目標，往往呈現相互沖突的關系。

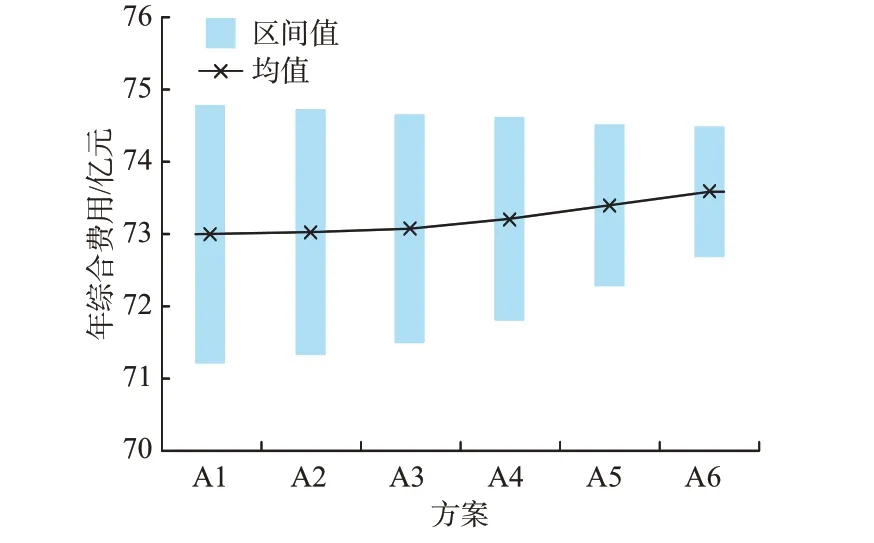
圖3 候選方案的年綜合費用區間Fig.3 Annualized comprehensive cost intervals of candidate schemes

為了綜合考慮和權衡各候選方案的年綜合費用區間的均值和偏差值，使用證據推理方法進行綜合決策。對各個候選方案的年綜合費用區間的均值和偏差值分別進行等級評估，并結合每個區間特性所對應的權重值，得到候選方案在各個評價等級上的分布情況。依據等級評估結果以及所設置的等級效用值，可以得到候選方案的綜合評估結果，即為綜合效用值。在評估過程中，為了更好地計及各場景的運行費用，采用風電出力的概率分布生成3 000個隨機場景，并依據年綜合費用區間均值和偏差值的概率分布情況來實現等級評估。評估的具體步驟如文獻［9］所述，評估結果如表1所示。將候選方案A1至A6的綜合效用值進行排序可知，方案A2為所選擇的最佳方案，綜合效用值是0.70。

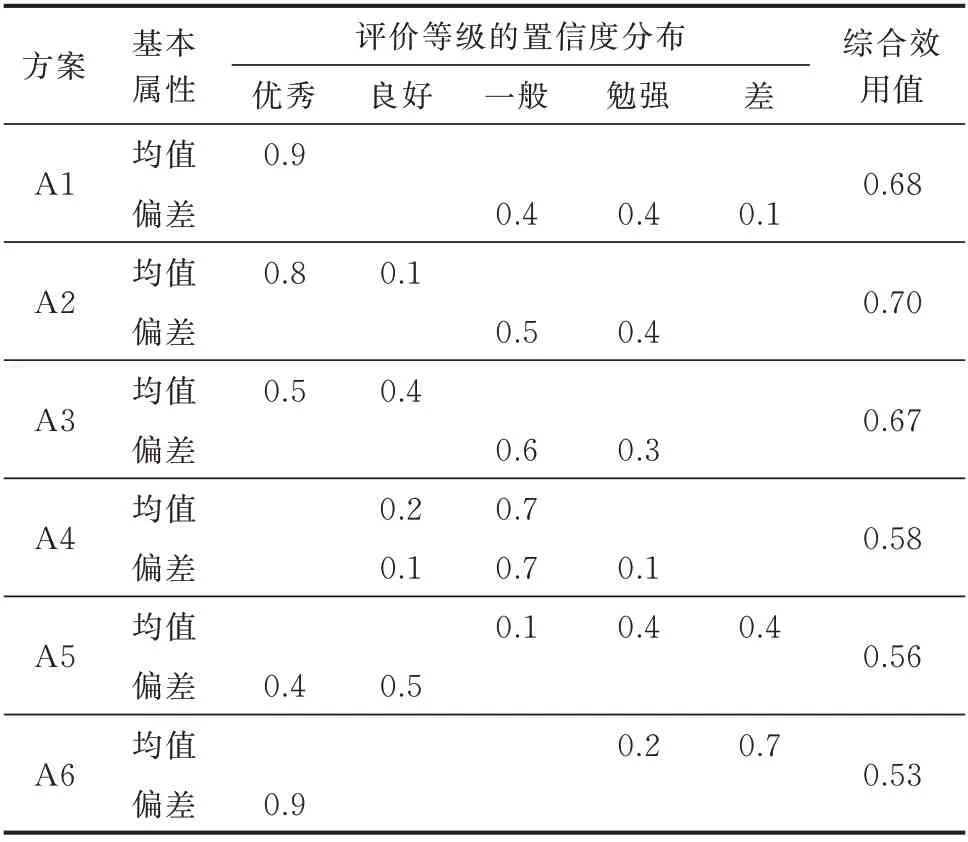
表1 候選方案的多屬性決策結果Table 1 Multi-attribute decision-making results of candidate schemes

表2給出了火電機組G1至G10的靈活性改造的候選方案A1至A6。表3給出了各候選方案中的機組改造容量。表4給出了各個候選方案中的各項費用。如表3所示，方案A1至A6中實施了調峰改造的機組容量分別為1 166.4、1 068.9、996.0、934.8、832.2、769.8 MW，各組方案中的改造容量呈現逐漸減少的趨勢。

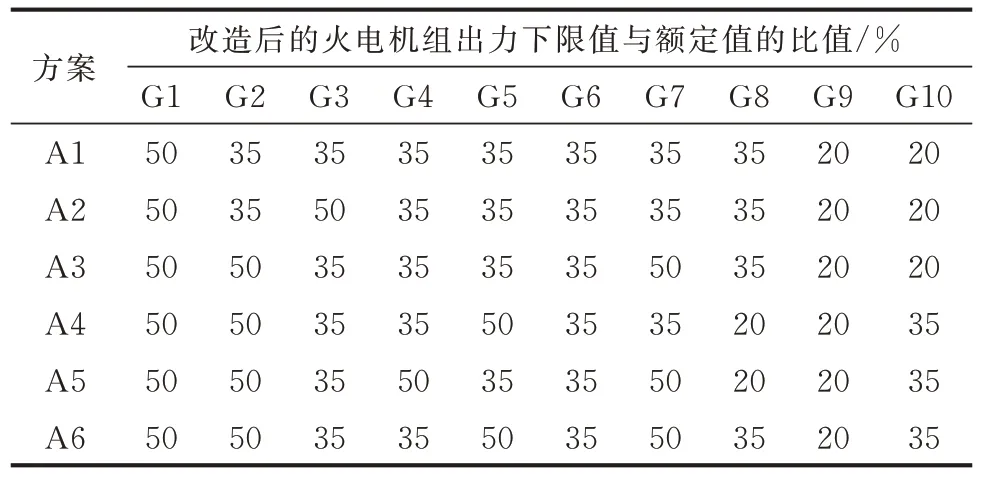
表2 火電機組靈活性改造候選方案Table 2 Candidate schemes for flexibility reformation of thermal power units

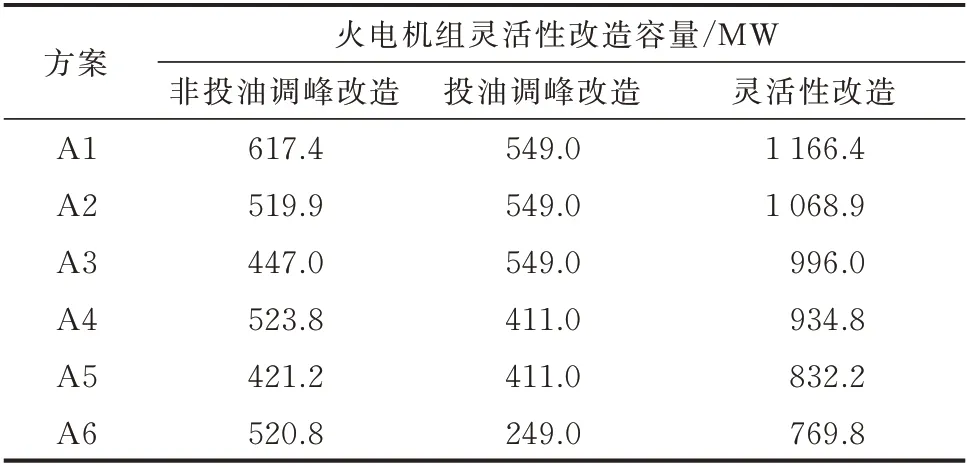
表3 候選方案的火電機組靈活性改造容量Table 3 Flexibility reformation capacity of thermal power units in candidate schemes

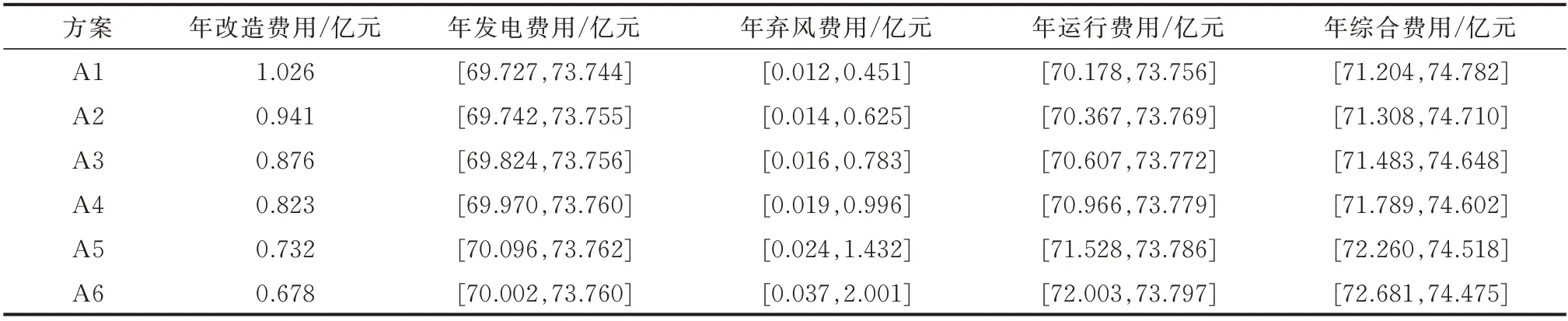
表4 火電機組靈活性改造候選方案的各項費用Table 4 Various costs for flexibility reformation of thermal power units in candidate schemes

方案A1具有最大的機組調峰改造容量，該方案盡可能地提高了系統中的風電消納量，減少了所有場景中的棄風費用，但由于方案中的調峰改造容量相對較大，引起機組調峰改造費用的增加，造成方案的綜合經濟性有所下降。最優方案A2適當地削減了機組調峰改造容量，雖然在部分運行場景中棄風費用有所增加，尤其是在風電出力波動范圍的上限，即風電大發場景下的棄風量最大，造成區間的下限略微上升，但大部分場景中的運行費用仍可以維持在較低值，結合方案中較低的機組調峰改造費用，該方案的綜合經濟性最優。方案A3至A6中的機組調峰改造容量進一步降低，系統中逐漸出現調峰容量不足的現象，各方案中的棄風量呈現大幅上升的趨勢。由于棄風費用相對較高，故各方案中的運行費用也隨之大幅上升，在方案A6中運行費用的增加已非常明顯。雖然各方案中的機組調峰改造費用會相應地有所下降，但由于棄風所引起的運行費用上升則更為明顯，造成各方案的經濟性逐漸變差。

綜上，在所得到的最優方案中提供了各機組的最優靈活性改造計劃以及改造容量。并且該方案可以實現對系統中大部分風電的消納，同時將部分造成經濟性不佳的風電予以丟棄，有效地折中了機組改造費用以及多個場景下的運行費用。

3.3 算法比較

當火電機組在深度調峰階段運行時，機組的單位發電成本明顯上升，各運行場景中將面臨單位發電成本不均衡的現象。本文以區間整體優化方法來綜合多個場景下的運行費用，從而提高模型在各場景下的適應性。同時，區間優化方法以全場景方式進行優化，從而提高模型在高風電接入比例下的潮流適應性。為了驗證所提出模型的有效性，與文獻［3］中所提出的模型進行了對比，該模型中僅考慮了火電機組靈活性改造方案在各月典型場景中的適應性。表5給出了2種優化方法得到的最優火電機組靈活性改造方案。表6給出了2種最優方案中的具體改造容量。方案A2和方案B1分別代表區間優化方法和確定性優化方法所得到的最優方案。

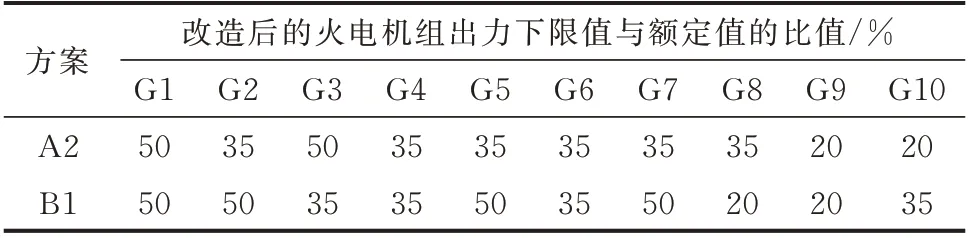
表5 兩種優化方法下的最優火電機組靈活性改造方案Table 5 Optimal flexibility reformation schemes of thermal power units with two optimization methods

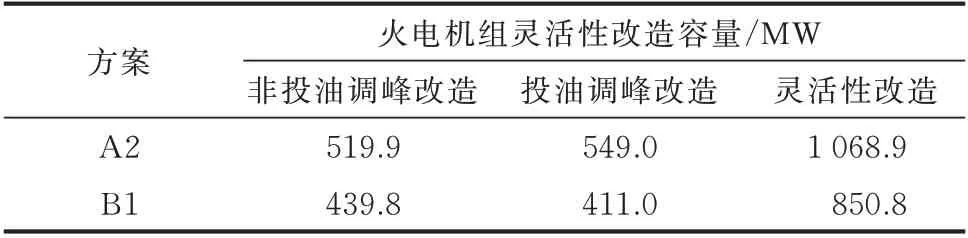
表6兩個最優方案中的火電機組靈活性改造容量Table 6 Flexibility reformation capacity of thermal power units in two optimal schemes

圖4給出了2種優化方法所得到的最優方案在不同風電出力場景中的年運行費用。如圖4所示，在常規風電出力場景中，方案A2和方案B1的年綜合費用相近；而在風電出力較大的場景中，方案A2的年綜合費用則明顯偏低。綜合多個風電出力場景下的年綜合費用，可表明方案A2的綜合經濟性更佳。為了更加直觀地表明2個方案在不同風電出力場景下的運行經濟性，選擇了3個典型風電出力場景并將這些場景中的各項費用列于表7中。其中方案A2和方案B1的年化靈活性改造費用分別為0.941億 元和0.749億元。

如表7和圖4所示，方案A2明顯降低了風電出力較大的一些場景中的運行費用以及棄風量。該現象主要由2個原因造成：第一，風電出力較大場景中的火電機組出力較低，故這些場景中的運行費用將明顯受到火電機組靈活性改造方案的影響，而在改造方案中選擇非投油調峰改造、投油調峰改造或者棄風下的單位運行費用會存在2～3倍的差距，所提出的模型以全場景優化方式計及了風電出力較大場景中的運行費用，有效降低了這些場景中的運行費用；第二，所提出的模型考慮了全場景下的潮流優化，所得到的機組改造方案具有更好的潮流適應性。如表5所示，方案A2適當增加了風電送出側的機組改造容量，從而有效降低了由于線路阻塞所造成的棄風懲罰費用。附錄A圖A3和圖A4分別給出了方案A2和方案B1中風電送出側線路1-2在冬季典型日中傳輸的有功功率，進一步說明了方案A2有效緩解了半夜時段和晚高峰時段的風電阻塞現象。

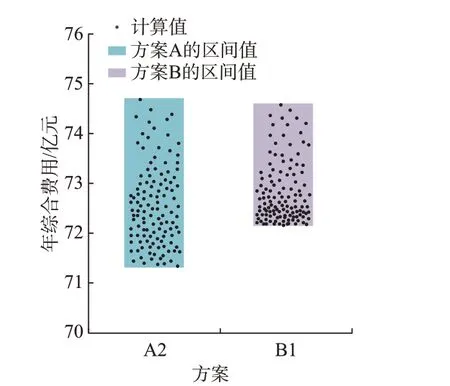
圖4 兩個最優方案在不同風電出力場景下的年綜合費用Fig.4 Annualized comprehensive costs of two optimal schemes in different wind power output scenarios

表7 兩個最優方案在不同出力場景下的費用Table 7 Costs of two optimal schemes in different wind power output scenarios

4 結語

本文提出了一個基于區間優化的火電機組靈活性改造規劃模型。該模型以火電機組靈活性改造費用和多場景運行費用的年綜合費用區間作為優化目標，并采用全場景優化方法來協同多個場景下的運行費用，從而得到一組綜合經濟性最優的火電機組靈活性改造方案。

所提出的模型提取了目標區間的均值和偏差值作為該區間的特征量，并將其選擇為模型中的2個優化子目標。為了綜合衡量目標區間的整體特性并篩選出最大限度滿足用戶需求的方案，在模型求解中使用了多目標尋優和多屬性決策2個步驟。首先，使用GSOMP算法來協同優化目標區間的均值和偏差值，從而生成多個候選方案，每個方案具有不同的年綜合費用區間特性。其次，使用多屬性決策方法對各個方案中的年綜合費用區間進行評估，依據各區間特征量的綜合表現選擇一組最優的方案。經算例驗證，所提出的模型有效提高了方案的綜合經濟性以及潮流適應性。在經濟性方面，由于火電機組在深度調峰階段中的單位發電成本變化明顯，故各不確定場景下的運行費用均將很大程度地依賴于改造方案。該模型采用全場景優化方法，明顯改善了風電出力較大場景下的運行費用，并維持了常規風電出力場景下的低運行費用，實現了方案的綜合經濟性提升。在潮流適應性方面，全場景優化方式能夠更好地適應高風電接入比例下的潮流不確定性，有效緩解了潮流阻塞現象并減少了各不確定場景下的棄風量。

需要說明的是，所提出的模型僅對機組靈活性改造的布點和方案進行了優化，并沒有考慮機組改造停運所造成的影響。實際上，機組進行靈活性改造具有一定的停運周期，而這部分停運周期會對電網的安全穩定運行造成一定的影響，故機組的靈活性改造應遵循一定的時序性。因此，下一步計劃開展具有時序特性的機組改造方案研究，以提供在保證電網安全穩定運行前提下可以逐步實施的火電機組靈活性改造方案。

附錄見本刊網絡版（http：//www.aeps-info.com/aeps/ch/index.aspx），掃英文摘要后二維碼可以閱讀網絡全文。