計及充電站無功補償的配電網日前-實時協調優化模型

王強鋼，田雨禾，王 健，胡方霞，周念成

（1.輸配電裝備及系統安全與新技術國家重點實驗室（重慶大學），重慶市 400044；2.重慶工商職業學院電子信息工程學院，重慶市 400052）

0 引言

近年來，環境污染和化石能源危機日益嚴重。綠色高效的電動汽車（electric vehicle，EV）對解決環境和能源問題起到了重要作用，EV接入配電網規模也日益增加［1-2］。但EV充電負荷具有隨機性和分散性，大規模EV接入配電網將產生不可忽視的影響，可能引起線路過載、網損增大或在負荷峰值時段造成配電網低電壓問題［3-4］。這對配電網安全穩定運行提出了挑戰，故需要對EV充放電進行控制。

針對EV的充放電控制，文獻［5］提出了EV分級充電控制策略用于降低配電網負荷峰谷差，文獻［6］建立了基于區域交通網和出行鏈模擬的EV充電負荷預測模型，文獻［7］建立了基于路網-電網交互式框架的EV充電負荷預測模型。據此，文獻［8］分析了在充電價格差異較大的情況下，通過電動汽車入網（V2G）技術能夠降低配電網運營成本。上述文獻集中于EV的有功功率控制，但EV通過充電樁的變流器接口接入電網，除有功功率外，還有一定的無功補償能力，可用于改善配電網電壓質量［9-10］。

配電網電壓調節主要有電容器組（capacitor bank，CB）和有載調壓變壓器（on-loadtap changer，OLTC）等裝置［11-12］。然而，傳統電壓調節裝置響應速度慢，應對EV不確定接入的能力較差。而充電樁具有靈活、快速的控制特性，對EV主動控制能夠有效地改善配電網的電壓分布［13］。文獻［14-15］利用雙向充電樁進行電壓調節，文獻［16］基于對充電樁的功率因數調節的策略來實現節點電壓穩定運行。前述文獻僅分析了充電樁的無功功率調節能力，但未與配電網已有的電壓調節裝置進行綜合調控。

當EV充放電控制時須考慮其荷電狀態（state of charge，SOC）約束，文獻［17］建立了考慮EV數量和SOC約束的EV可調度模型，文獻［18］建立了考慮移動儲能特性的EV模型，但僅考慮EV統一的SOC邊界約束（即固定的最大和最小區間），未考慮不同EV的SOC邊界差異。對此，文獻［19］提出了計及SOC邊界的EV接入配電網的實時優化調度方法，在此基礎上，文獻［20］提出了一種基于聚合商模型的大規模EV的SOC評估方法。但是，現有研究采用的SOC邊界沒有計及EV前一時刻SOC的影響，可能造成鄰近SOC邊界時EV的功率分配不當導致SOC越限。

為解決以上問題，本文提出了一種計及充電站無功補償的配電網日前-實時協調優化模型。日前優化模型以配電網運營成本最低為優化目標，有載調壓變壓器和電容器組等設備調節限制為約束條件。然后，實時優化以日前優化結果為運行參考點，通過多層優化模型之間協調互補，實現配電網、電動汽車充電站（electric vehicle charging station，EVS）和EV之間功率的有效分配。此外，為保證EV離開時達到期望SOC，充分考慮了SOC邊界條件。最后，通過算例分析驗證了該模型的有效性。

1 日前-實時協調優化框架

計及充電站無功補償的配電網日前-實時優化框架如附錄A圖A1所示。框架由日前優化和實時優化兩部分組成，日前-實時優化框架中配電網、充電站和EV的具體執行步驟如下。

步驟1：在日前優化部分，充電站將所有EV數據的概率分布傳輸給配電網，包括初始時刻、離開時刻、初始SOC和離開時的SOC。

步驟2：配電網根據信息，結合分時電價、負荷需求曲線、網絡參數、有載調壓參數和電容器組參數，建立了配電網運營成本最低的優化模型。

步驟3：將充電站日前有功功率、電容器組投切和有載調壓擋位作為實時優化的參考運行點，以降低實時優化中配電網的運營成本。

步驟4：在實時優化部分，當EV接入充電樁后，充電站根據EV的初始時刻、離開時刻、初始SOC和離開時的SOC，計算出其有功功率范圍和SOC范圍，然后將信息提供給配電網。

步驟5：配電網根據信息，結合充電站日前有功功率，建立以充電站有功功率偏差最小為目標的優化模型，計算出充電站的有功功率。

步驟6：充電站根據信息建立以EV的總無功容量最大為目標的優化模型，計算出EV的有功功率和最大無功容量。

步驟7：充電站根據EV的最大無功容量，計算出充電站的最大無功容量，然后將信息提供給配電網。

步驟8：配電網根據信息建立以網損最小為目標的優化模型，計算出充電站實際的無功功率。

步驟9：充電站根據信息建立以EV的總視在功率最小為目標的優化模型，計算出EV實際的無功功率。

步驟10：EV在步驟6和9中執行來自充電站的有功和無功功率信號。

步驟11：下一個時間周期的EV參數更新時，重復步驟4至步驟10。

2 日前優化模型建立

2.1 EVS日前功率模型

EVS日前功率模型是基于整體EV數據的概率分布進行建模，不同EV的充放電狀態不同，而不同狀態對應的損耗模型也有所區別。在日前優化中忽略了充放電損耗，表達式為：

2.2 日前優化模型

日前優化模型約束條件包括潮流方程、安全約束、有載調壓變壓器約束和電容器組裝置約束。

1）潮流方程

文獻［21-22］采用線性化DistFlow模型來表示潮流方程，且考慮了系統網損。本文基于DistFlow線性化方程，配電網的潮流方程表達式為：

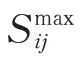
3）有載調壓變壓器約束

本文對有載調壓作了簡化處理，將變壓器模型等效為一個節點處理，即不考慮變壓器支路，節點電壓變成可調變量，即

4）電容器組裝置約束

本文假設每組電容器的調節容量一定，通過調節投運組數來優化電網運行情況，即

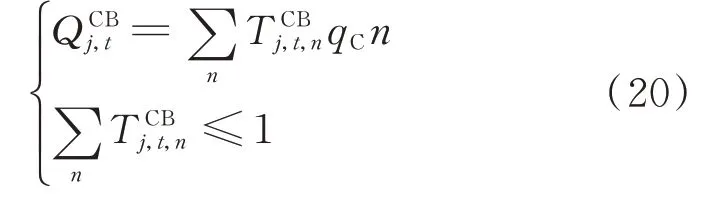
式中：ct為分時電價；cL為損耗成本；cC為電容器組無功補償成本；cQ為EV無功成本；Pg，t為從上級電網注入配電網的有功功率；E為網絡中所有支路集合；NCB為包含電容器組裝置的節點集合；NEVS為包含充電站的節點集合；cT為每次有載調壓的成本；nT為T時段有載調壓的總次數。

3 實時優化模型建立

3.1 EV功率模型

EV的SOC表 示 為：

式中：ex，y，t為t時段充電站x中第y個EV的SOC；在實時優化模型中，時間間隔Δt取15 min。

當EV接入充電樁時，通過EV上的電池管理系統獲取電池當前SOC、EV停留時間和離開時期望的SOC，來確定SOC邊界［19-20］。如圖1所示，紅色和綠色曲線分別表示SOC的上邊界和下邊界。

圖1 EV的SOC動態邊界Fig.1 Dynamic SOC boundary for EV

在本文的模型中，配電網首先是調度充電站，如果充電站的SOC邊界僅基于EV的SOC邊界，則可能會增加其SOC邊界的范圍，導致優化時可能造成鄰近SOC邊界時EV的功率分配不當導致SOC越限，而不能確保EV離開時達到期望的SOC。為了解決此問題，考慮EV前一時刻的SOC。SOC動態邊界表達式為：

式 中：NEV為 充 電 站x中EV的 集 合；Ex，t為t時 段 充電站x內所有EV的SOC總和。

3.3 實時優化模型

實時優化模型包括配電網和充電站的有功和無功優化模型。

1）模型1為配電網有功優化模型

當EV接入充電樁后，提供電池當前SOC、停留時間以及離開時期望的SOC等信息，充電站根據EV信息產生其電池側功率范圍和SOC范圍。配電網基于充電站提供的信息和充電站日前有功功率建立優化模型，配電網有功優化模型優化目標是充電站的有功功率偏差最小。

由此，該目標函數線性化為：

約束條件為式（33）至式（36）。

模型1是被設計來決定每個充電站電池側的實際功率，同時有功功率偏差最小能夠有效減少配電網運營成本。

2）模型2為充電站有功優化模型

在確定充電站電池側的有功功率之后，通過以下優化模型可以得到EV電池側的有功功率，即

約束條件為式（23）、式（26）至式（30），以及式（39）和式（40）。

模型2的優化目標是EV的總無功容量最大，而且確保EV有足夠的無功補償能力。

3）模型3為配電網無功優化模型

充電站將基于EV的無功容量和有功功率提供給配電網，通過以下優化模型可以得到充電站的無功功率，即

約 束 條 件 為 式（10）至 式（21）和 式（31）、式（32）。

模型3的優化目標是網損最小。

4）模型4為充電站無功優化模型

基于充電站的無功功率，通過以下優化模型可以得到EV的無功功率，即

約束條件為式（24）、式（25），以及式（43）和式（44）。

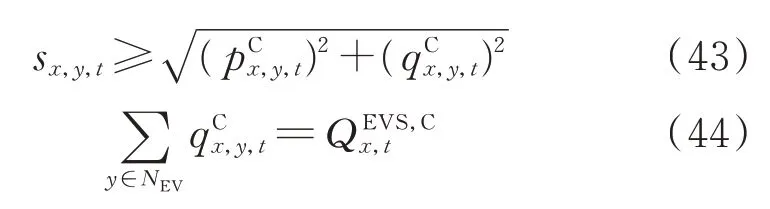
式 中：sx，y，t為t時 段 充 電 站x中 第y個EV的 視 在功率。

模型4的優化目標是EV的總視在功率最小，同時避免充電樁的過載情況。

式（3）、式（15）、式（17）、式（25）、式（32）、式（39）和式（43）是非線性方程，會增加優化模型求解的難度，文獻［23］通過圓約束和二次平方項線性化的方法對方程進行線性化處理。本文采用分段線性化法將日前優化和實時優化模型線性化處理。

4 算例分析

4.1 算例基礎數據

本文采用IEEE 33節點系統來驗證模型的有效性。算例是采用MATLAB R2018a-YALMIP仿真平臺進行測試，并調用CPLEX12.10.0版本進行優化求解，電腦的硬件參數為主頻3 GHz、內存8 GB［24］。

IEEE 33節點系統如圖2所示，節點1為有載調壓變壓器，初始擋位為3，有5個調節擋位，調節范圍為［0.98，1.02］。節點3、8、14、19、23、30為EVS，每個節點有100臺EV進行充電，充電樁功率容量為7 kVA，電池容量為60 kW·h，充放電的效率為95%。EV的到達和離開概率分布分別符合正態分布N（19 h，12）和均勻分布U（6 h，8 h），初始SOC符合正態分布N（0.6，0.12），離開時的SOC值都設為0.95。節點10、16、28安裝有電容器組投切裝置，其中每個節點為4組，每組大小為0.05 Mvar。節點電壓限制是［0.95，1.05］p.u.。負荷需求和分時電價如附 錄A圖A2所示，EV的 控制周期為17：00—次日08：00。

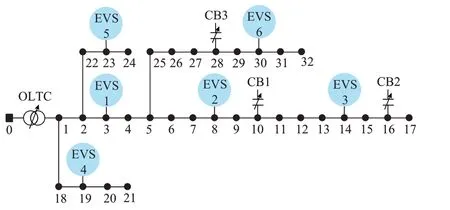
圖2 IEEE 33節點系統Fig.2 IEEE 33-bus system

4.2 日前優化結果分析

為了驗證充電站無功補償在日前優化模型中的有效性，設立如下3個案例進行分析。

案例1：無有載調壓和電容器組投切裝置，EV的無功功率不可注入。

案例2：投入有載調壓和電容器組投切裝置，EV的無功功率不可注入。

案例3：投入有載調壓和電容器組投切裝置，EV的無功功率可注入。

表1所示為不同案例日前優化模型的仿真結果。

表1 日前優化結果Table 1 Results of day-ahead optimization

案例1沒有考慮有載調壓、電容器組投切裝置和EV無功成本，購電成本、網損成本和總成本在3個方案中最高。相比于案例1，案例2增加了有載調壓和電容器組投切裝置，購電成本、網損成本和總成本都有所降低。在案例3中，注入EV的無功功率使得購電成本、網損成本、電容器組成本進一步減少，總成本在3個案例中最低。

附錄A圖A3為不同案例日前優化模型的配電網電壓曲線。在案例1中，平均電壓和最低電壓均存在低于電壓下限的情況；案例2通過投入有載調壓和電容器組投切裝置提升了配電網節點電壓，節點28～32的最低電壓低于電壓下限，如附錄A圖A4所示，有載調壓調節一次到5擋，電容器組投切組數較多；案例3通過增加EV的無功功率進一步改善配電網節點電壓，相比于案例2，所有節點電壓均在電壓下限之上，有載調壓調節擋位沒有調節，電容器組投切組數大幅減少。

4.3 實時優化結果分析

實時優化模型被稱為案例4。案例4中購電成本、網損成本、電容器組成本、有載調壓成本、EV無功成本和總成本分別為42 592、3 521、115、0、631、46 859元，總成本比案例3更高，因為日前優化模型是基于整體EV概率分布的，僅考慮到EV的數量、電池容量和充電樁功率容量，忽略了每個充電樁的有功和無功功率約束，以及EV的SOC邊界，會造成日前優化模型中充電站提供的無功補償范圍更大，方案3中購電成本和網損成本更低一些。附錄A圖A5為案例4的配電網電壓曲線，可見所有節點電壓都大于電壓下限，電壓曲線與案例3大致相同，證明日前優化模型能夠作為實時優化模型的參考對象。

案例4中充電站的有功和無功功率如附錄A圖A6所示。17：00—20：00處于負荷高峰階段，充電站的有功功率很小，20：00—21：00充電站有功功率開始注入配電網。在負荷低谷階段，充電站有功功率從24：00開始增加到次日05：00，后因EV逐漸離開充電站，有功功率從05：00開始降低。充電站的無功功率通常為負，說明EV在配電網進行無功補償，在高負荷需求時段（19：00—23：00）有大量無功功率注入配電網。

4.4 求解效率分析

通過分段線性化法將日前優化和實時優化模型線性化處理，日前優化模型是線性規劃模型，實時優化的模型1到模型4是線性規劃或者混合整數線性規劃模型［23］。日前和實時優化求解時間如表2所示。日前優化求解時間小于10 s，實時優化求解時間小于0.1 s，能夠滿足EV的實時優化運行要求。

表2 日前和實時優化求解時間Table 2 Solving time of day-ahead and real-time optimization

5 結語

本文提出了一種計及充電站無功補償的日前-實時協調優化模型，通過算例分析，結果表明：

1）日前優化模型能夠提供配電網運營成本最小的優化結果，基于日前優化結果和EV實時參數建立實時優化模型，日前和實時優化之間緊密聯系，綜合提高了配電網經濟性；

2）當注入EV的無功功率時，配電網運營成本最低，EV通過充電樁分擔了一部分無功補償需求，使得電容器組補償的無功功率和有載調壓調節次數有所下降，對配電網電壓調節有著積極的影響；

3）在滿足期望的SOC需求基礎上，EV可根據分時電價錯開負荷高峰期進行充電，避免增加配電網負擔。

附錄見本刊網絡版（http：//www.aeps-info.com/aeps/ch/index.aspx），掃英文摘要后二維碼可以閱讀網絡全文。