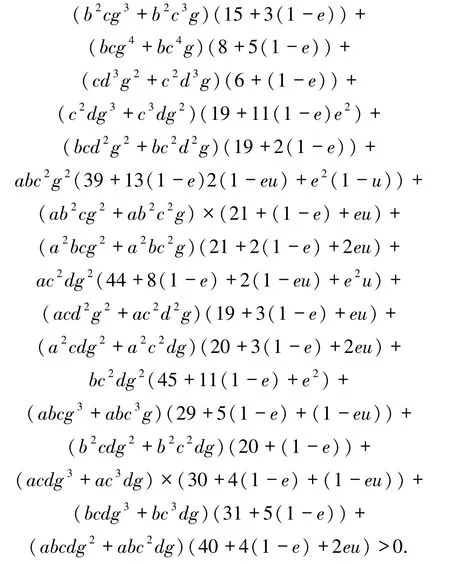敏感型和耐藥型HIV毒株感染模型的全局動(dòng)力學(xué)

陳 偉， 滕志東

（新疆大學(xué) 數(shù)學(xué)與系統(tǒng)科學(xué)學(xué)院，新疆 烏魯木齊830046）

眾所周知，HIV病毒侵入人體后，人體的免疫功能遭到破壞，最終導(dǎo)致人體死亡，1982年被正式命名為艾滋病.艾滋病毒有3種傳播方式：血液傳播、母嬰傳播和性接觸傳播.目前，許多具有特異性免疫反應(yīng)的病毒動(dòng)力學(xué)研究日益受到重視，這些研究對(duì)預(yù)防和控制艾滋病有一定的指導(dǎo)作用［1-6］.

在治療HIV感染患者方面，有4類抗逆轉(zhuǎn)錄病毒（ARV）藥物：

1）核苷/核苷酸逆轉(zhuǎn)錄酶抑制劑（NRTIs），

2）非核苷逆轉(zhuǎn)錄酶抑制劑（NNRTIs），

3）蛋白酶抑制劑（PIs），

4）進(jìn)入/融合抑制劑（EIs）［7］.每種藥物針對(duì)病毒生命周期的不同階段.HIV耐藥的出現(xiàn)最早是由一些核苷抑制劑記錄的，這些抑制劑通過其作為DNA鏈終止劑的活性抑制病毒復(fù)制［8］.在臨床中，艾滋病毒耐藥性可由耐藥突變體向易感個(gè)體傳播或通過在治療期間產(chǎn)生的突變而產(chǎn)生.Rong等［9］提供了一個(gè)理論框架，用于探索在使用其他HCV蛋白酶抑制劑或聚合酶抑制劑治療期間，預(yù)先存在的突變變體的患病率和耐藥性的演變.

為了研究HIV感染患者在治療過程中產(chǎn)生耐藥性的機(jī)制，Rong等［7］提出了如下包括敏感型和耐藥型毒株的動(dòng)力學(xué)模型

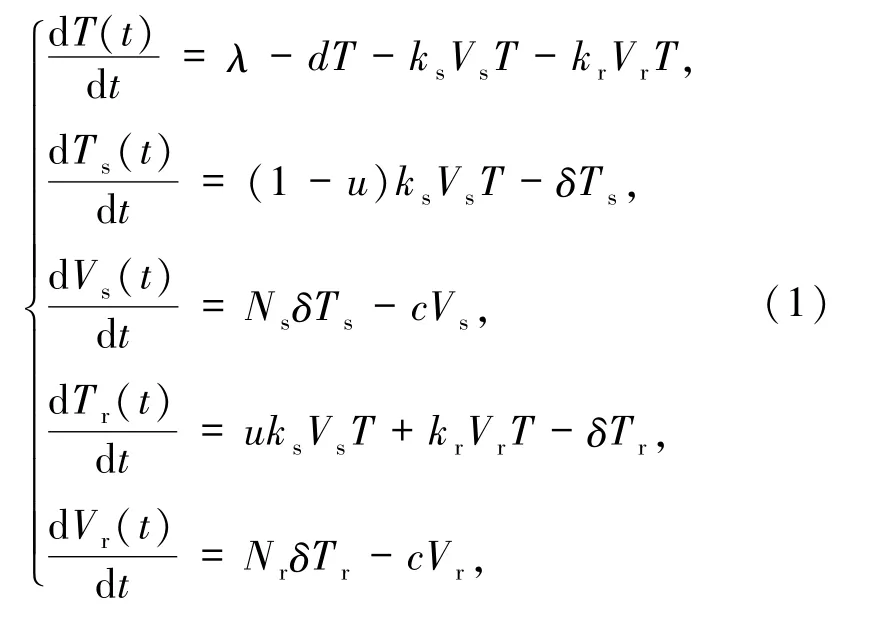
其中，T（t）為未感染細(xì)胞在時(shí)間t的濃度，Ts（t）為敏感毒株感染細(xì)胞在時(shí)間t的濃度，Tr（t）為耐藥毒株感染細(xì)胞在時(shí)間t的濃度，Vs（t）為敏感毒株在時(shí)間t的濃度，Vr（t）為耐藥毒株在時(shí)間t的濃度，λ為未感染細(xì)胞的補(bǔ)充率，d為未感染細(xì)胞的病死率，ks為敏感毒株感染細(xì)胞的感染率，kr為耐藥毒株感染細(xì)胞的感染率，δ為感染細(xì)胞的病死率，Ns為敏感毒株的釋放率，Nr為耐藥毒株的釋放率，c為游離病毒的清除率.

在模型（1）中，參數(shù)u（0＜u＜1）是病毒RNA逆轉(zhuǎn)錄成原病毒DNA（簡(jiǎn)稱SR轉(zhuǎn)化）過程中，敏感型毒株發(fā)生突變并且產(chǎn)生耐藥性的轉(zhuǎn)化率.需要注意的是，在開始治療之前，宿主體內(nèi)就存在大量的敏感毒株，因此從耐藥型向敏感型毒株的后向突變就可被忽略［10-11］.為了準(zhǔn)確地計(jì)算出模型的平衡點(diǎn)，以及確定模型平衡點(diǎn)的穩(wěn)定性，生物動(dòng)力學(xué)的入侵閾值，即傳染病中基本再生數(shù)的概念起著決定性的作用［12］.

文獻(xiàn)［7］僅研究了模型（1）中無病平衡點(diǎn)，具有耐藥型毒株感染的邊界平衡點(diǎn)以及共存平衡點(diǎn)的存在性和局部穩(wěn)定性［7］（命題1和命題2），全局動(dòng)力學(xué)包括平衡點(diǎn)的全局漸近穩(wěn)定性和HIV感染模型的一致持續(xù)性都沒有考慮.因此，在本文中，將對(duì)這些問題進(jìn)行深入研究.對(duì)無病平衡點(diǎn)、具有耐藥型毒株平衡點(diǎn)、共存平衡點(diǎn)的局部及全局穩(wěn)定性和HIV感染模型的一致持續(xù)性建立了一系列的閾值準(zhǔn)則.

1 基本性質(zhì)

對(duì)任意整數(shù)n＞0，定義

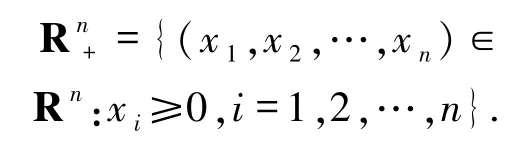
模型（1）的初始條件可表示為

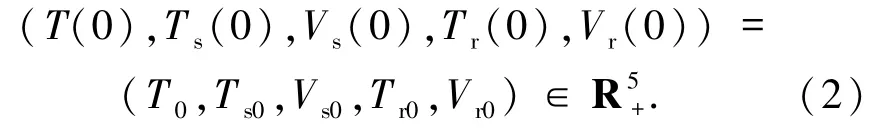
關(guān)于模型（1）解的正性和有界性，有定理1.

定理1對(duì)任何初始值

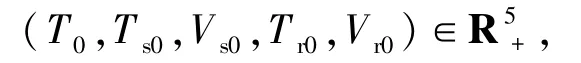
模型（1）具有初始條件（2）的解

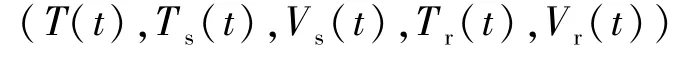
在t∈［0，∞）上有定義，非負(fù)且最終有界.

證明首先，證明解的非負(fù)性.顯然，只需要證明對(duì)滿足任意正初始值（T0，Ts0，Vs0，Tr0，Vr0）的解（T（t），Ts（t），Vs（t），Tr（t），Vr（t））也是正的.定義m（t）=min｛T（t），Ts（t），Vs（t），Tr（t），Vr（t）｝，則有m（0）＞0.用反證法.假設(shè)存在一個(gè)t*＞0使得m（t*）=0，并且對(duì)所有的t∈［0，t*）有m（t）＞0，則有以下5種情形：

1）m（t*）=T（t*），2）m（t*）=Ts（t*），

3）m（t*）=Vs（t*），

4）m（t*）=Tr（t*），

5）m（t*）=Vr（t*）.

對(duì)于情形1），由于當(dāng)t∈［0，t*）時(shí)有m（t）＞0，則從模型（1）的第一個(gè)方程有

因此，可以得到0=Ts（t*）≥Ts（0）e-δt*＞0，矛盾.與上述論證類似，可以得到情形3）、4）和5）都是矛盾的，這表明m（t）總是正的.因此，解（T（t），Ts（t），Vs（t），Tr（t），Vr（t））是非負(fù)的.

下面證明解的最終有界性.定義Lyapunov函數(shù)

這說明解（T（t），Ts（t），Vs（t），Tr（t），Vr（t））也是最終有界的.定理得證.

根據(jù)在文獻(xiàn)［12］中提出的傳染病基本再生數(shù)的概念，定義如下敏感型毒株感染基本再生數(shù)Rs和耐藥型毒株感染基本再生數(shù)Rr為：

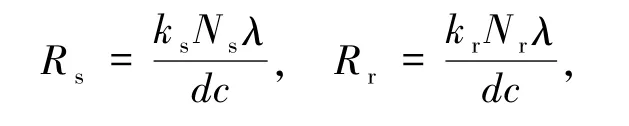
其中，1/c表示毒株i（i=r，s）的平均生命周期；λ/d表示毒株i在感染過程開始時(shí)，少量病毒感染易感細(xì)胞的感染細(xì)胞數(shù)量（接近于無感染穩(wěn)態(tài)）；ki Ni代表一個(gè)i型毒株在其平均存活時(shí)間內(nèi)產(chǎn)生的病毒顆粒數(shù)量.將這些量全部乘積起來就可以得到一個(gè)i型毒株感染細(xì)胞產(chǎn)生新的感染細(xì)胞的數(shù)量，也就是Ri.

下面討論模型（1）平衡點(diǎn)的存在性.平衡點(diǎn)可以由下列方程組得到

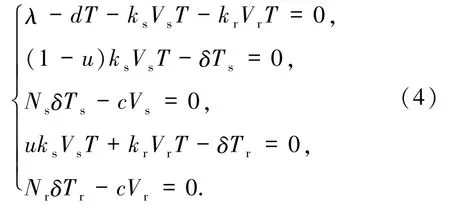
通過求解方程組（4），很容易得到定理2.

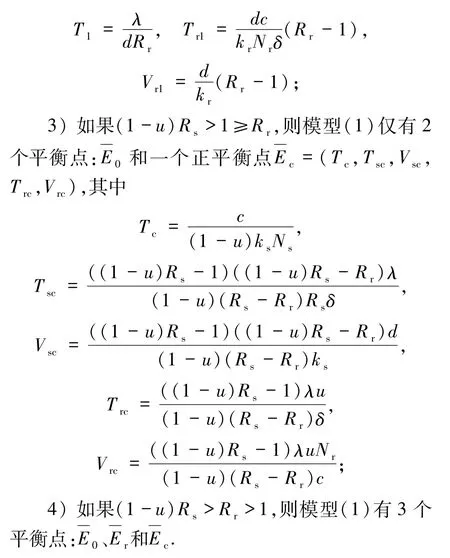
2 全局穩(wěn)定性

令E=（T，Ts，Vs，Tr，Vr）是模型（1）的任意平衡點(diǎn)，則在平衡點(diǎn)E處的Jacobi矩陣如下

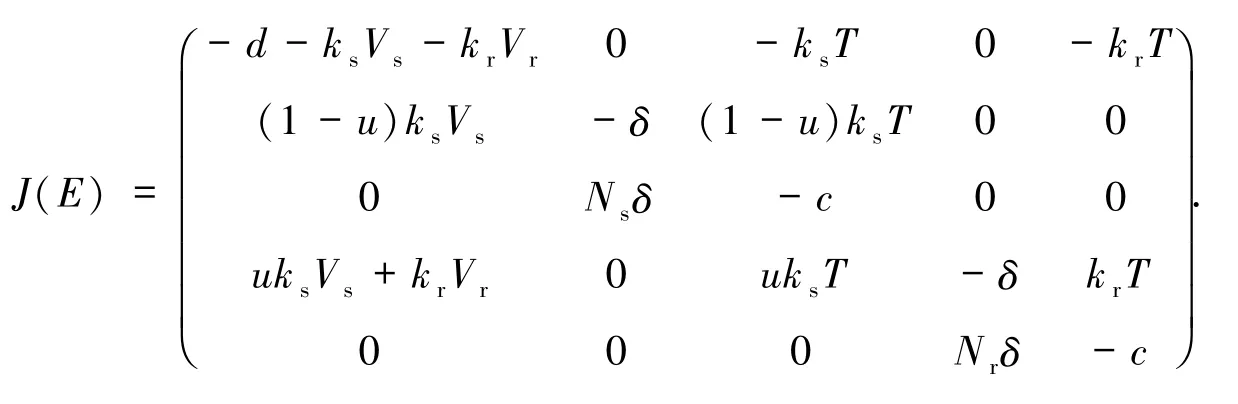
（5）式的一個(gè)根為X1=-d.當(dāng)（1-u）Rs＜1且Rr＜1時(shí)，方程

3 一致持續(xù)性

定理6 如果（1-u）Rs＞max｛1，Rr｝，則模型（1）是一致持續(xù)的.也就是說，存在一個(gè)正常數(shù)δ，使得對(duì)模型（1）的任意正解（T（t），Ts（t），Vs（t），Tr（t），Vr（t）），都有

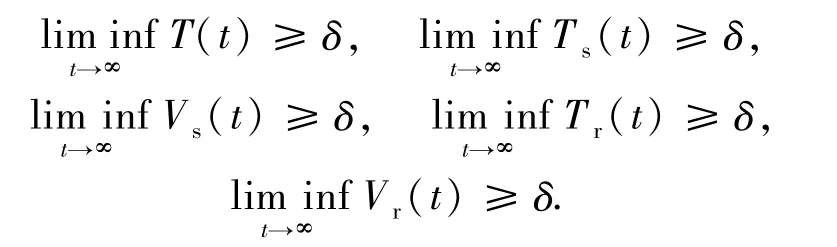
證明對(duì)任意

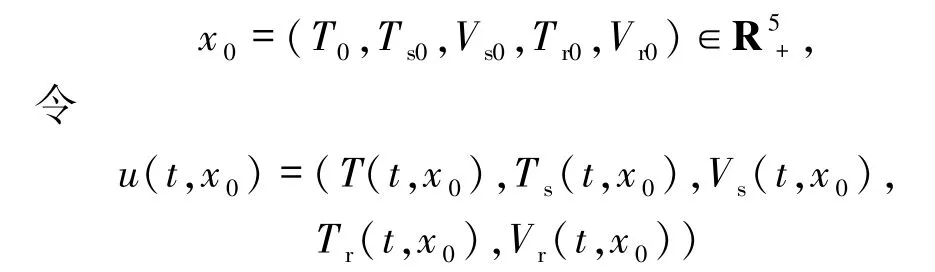
是模型（1）具有初始條件u（0，x0）=x0的解.從定理1的證明可以得到

4 數(shù)值模擬

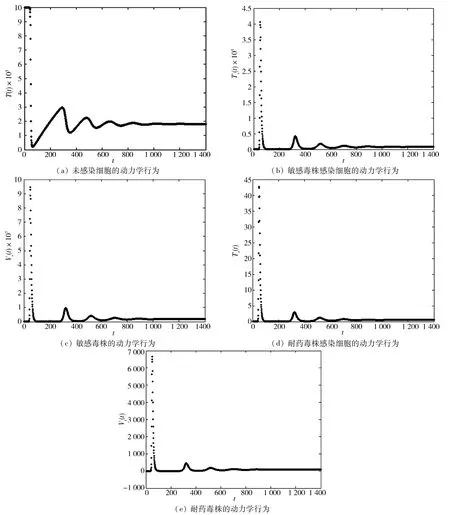
圖1 HIV感染模型的動(dòng)力學(xué)行為Fig.1 Dynamical behaviors of HIV infection model

表1 模型（1）的初始值Tab.1 The initial values of model（1）

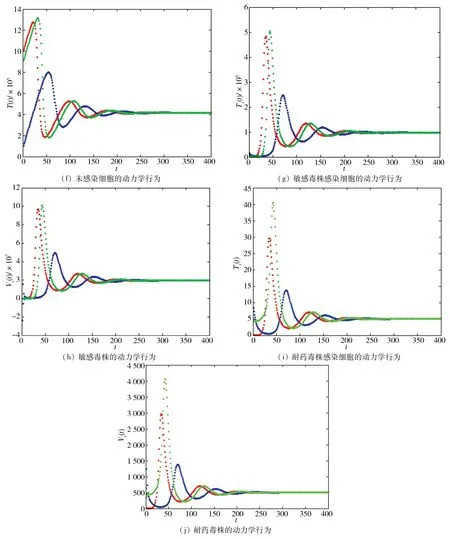
圖2 HIV感染模型的動(dòng)力學(xué)行為Fig.2 Dynamical behaviors of HIV infection model

5 結(jié)論

本文主要研究了敏感型和耐藥型2種毒株的HIV感染模型的全局動(dòng)力學(xué).敏感毒株在逆轉(zhuǎn)錄過程中會(huì)發(fā)生突變并產(chǎn)生耐藥性.主要結(jié)果在定理1～定理6中給出.具體地說，在定理1中得到解的正性和有界性，在定理2中計(jì)算出耐藥型毒株感染平衡點(diǎn)和共存平衡點(diǎn)，定理3～定理5中分別得到每個(gè)平衡點(diǎn)的局部和全局漸近穩(wěn)定的充要閾值條件，在定理6中建立HIV感染模型的一致持續(xù)性.

同樣也有很多問題值得更深地去研究.首先，注1～注3考慮了一個(gè)有趣的開問題就是能否在對(duì)應(yīng)的條件下建立平衡點(diǎn)的全局漸近穩(wěn)定性.其次，研究更加復(fù)雜的模型，比如具有飽和發(fā)生率的2種毒株感染模型［15-16］.此外，具有空間擴(kuò)散的多毒株感染模型平衡點(diǎn)全局穩(wěn)定問題和具有年齡結(jié)構(gòu)感染模型的動(dòng)力學(xué)行為［17-18］等問題仍然值得去研究.