交換半環上有限生成半模的基數問題

張小梅， 舒乾宇

（四川師范大學 數學科學學院，四川 成都610066）

對于半環上半模結構的研究已經有了很長的歷史.1979年，Cuninghame-Green［1］在max-plus代數中構建了類似于線性代數的一系列理論，之后研究者們又在該理論上得到了許多類似于線性代數的結論［2-6］.2007年，Di Nola等［7］在MV-max代數中構建了半環上半模的結構，引入了許多定義并提出了一些開問題，其中之一就是每組基的基數是否相同.這個問題在max-plus代數中已經得到了證實［8］.2011年，Zhao等［9］在join半環中給出每組基有相同基數的充要條件.2014年，Tan［10］在交換半環中給出每組自由基有相同基數的充要條件.同年，Shu等［11］在交換半環上的n-維半線性空間中給出每組基有相同基數的充要條件.2016年，Tan［12］討論了自由集及其性質.區別于模的是，在半模中，線性無關的向量組不一定是自由的.因此，研究者們把線性無關分成了半線性相關和強線性無關2類.但對交換半環上強線性無關集的性質和含有強線性無關基的有限生成半模的基數問題至今沒有討論，本文將在交換半環上對強線性無關集的性質和含有強線性無關基的有限生成半模的基數問題進行討論.

1 預備知識

為了下面討論方便，本節將給出一些定義和基本結論.

定義1.1［13］半環L=（L，+，·，0，1）是滿足下述性質的代數結構：

1）（L，+，0）是交換幺半群；

2）（L，·，1）是幺半群；

3）對任意的r，s，t∈L，滿足r·（s+t）=r·s+r·t和（s+t）·r=s·r+t·r；

4）對任意的r∈L，有0·r=r·0=0成立；

5）0≠1.

若對任意的r，r′∈L，滿足r·r′=r′·r，則稱L是交換半環.

例1.11）設N是所有自然數構成的集合，N連同普通的加法和乘法運算構成交換半環.

3）模糊代數〈［0，1］，max，min，0，1〉是交換半環.

定義1.2設L=〈L，+，·，0，1〉是半環，M=〈M，+M，0M〉是加法交換幺半群.若外積*：L×M→M滿足對任意的r，r′∈L和a，a′∈M都有：

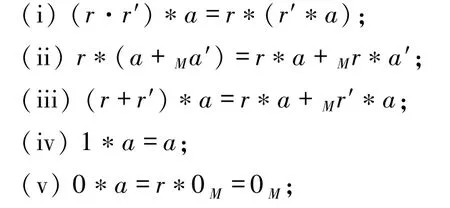
則稱〈L，+，·，0，1；*；M，+M，0M〉為左L-半模.

類似的可以定義右L-半模，其中外積的定義為M×L→M.

為了方便，在不會引起混淆的情況下，在左L-半模〈L，+，·，0，1；*；M，+M，0M〉中，對任意的r∈L，a∈M，將用r a代替r*a，用0代替0M.

若無特別說明，下文中的半模都指左L-半模.令=｛1，2，…，n｝，其中n是任意正整數.用｜S｜表示集合S中元素的個數，稱為集合S的基數.半模中的元素稱為向量，半環中元素稱為標量或系數.前者用粗體表示以區別標量.可以構造出下面一些半模.

例1.2（a）設L=〈L，+，·，0，1〉是半環.對n≥1，令

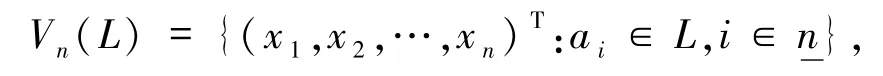
其中（x1，x2，…，xn）T表示（x1，x2，…，xn）的轉置.對任意的x=（x1，x2，…，xn）T，y=（y1，y2，…，

設N是L-半模M的非空子集，如果N中的元素關于M中的加法和乘法運算封閉，那么稱N是M的子半模.對M的任意子半模N1、N2，稱N1+N2=｛x+y：x∈N1，y∈N2｝和N1∩N2=｛x：x∈N1且x∈N2｝分別為子半模的和與子半模的交.顯然子半模的和與子半模的交還是子半模.

設S是L-半模M的非空集合，在M中所有包含S的子半模的交仍為M的子半模，稱為是由S生成的子半模，記作Span（S），容易證明合.如果S=｛x1，x2，…，xm｝，那么

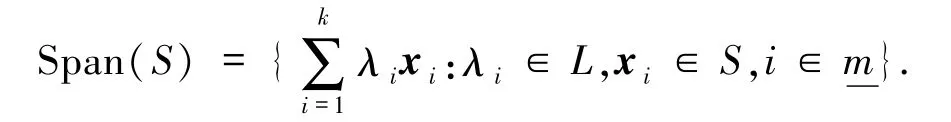
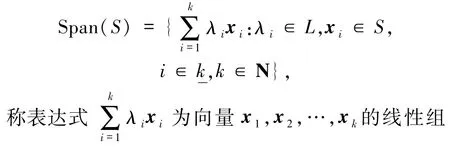
若Span（S）=M，則稱S是M的生成集.若M中存在有限生成集，則稱M是有限生成半模.稱M中生成集的最小基數為M的秩，記作r（M）.顯然在有限生成半模M中，秩是存在的.

定義1.3［7］在L-半模M中，單個向量x是線性無關的.若向量組x1，x2，…，xn，n≥2中任一向量都不能由其余向量線性表示，則稱向量組x1，x2，…，xn是線性無關的.否則，稱向量組x1，x2，…，xn線性相關.

定義1.4［13］在L-半模M中，線性無關的生成集稱為M的基.

定義1.5［10］設x1，x2，…，xn是M的向量組.對任意的α∈M，若α最多用一種方法由x1，x2，…，xn線性表出，則稱向量組x1，x2，…，xn是自由的.若Span（x1，x2，…，xn）=M，則稱該向量組為半模M的自由基.

用Mm×n（L）表示L中所有m×n矩陣組成的集合.特別地，令Mn（L）=Mn×n（L）.對任意的A=（aij），B=（bij）∈Mm×n（L）和C=（cij）∈Mn×l（L），定義運算如下：

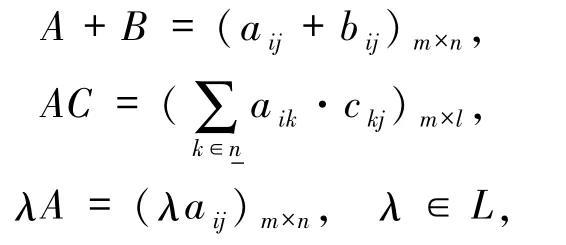
則（Mn（L），+，·，On，In）是一個半環，其中，

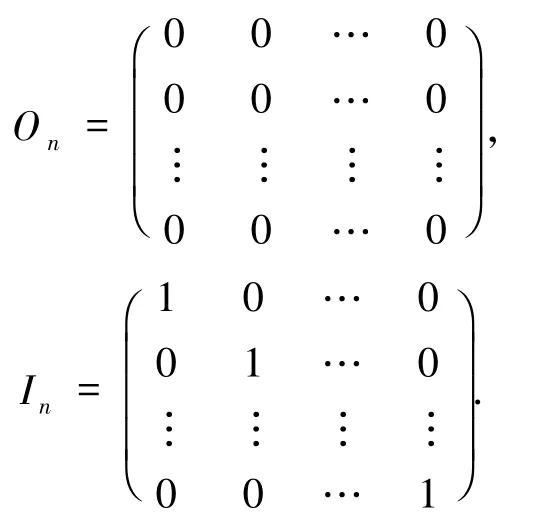
定義1.6［13］稱A∈Mn（L）是左可逆的（或右可逆的），如果存在B∈Mn（L）使得AB=In（或BA=In）.若A既是右可逆的又是左可逆的，則稱A是可逆的.

攤鋪過程的質量控制應首先從攤鋪設備抓起，如果條件許可，應盡量選用性能穩定、技術先進的攤鋪機，全套設備盡量使用相同品牌。面層施工必須全幅攤鋪，采用浮動基準梁控制攤鋪厚度和平整度。當路面滯水時，應暫停施工；氣溫低于10℃時，應停止攤鋪；氣溫低于15℃時，應控制瀝青混凝土的最大運距，以保證碾壓溫度在規定的范圍之內；未經壓實即遭雨淋的瀝青混凝土應全部清除，更換新料。

定義1.7［10］設A=｛x1，x2，…，xm｝和B=｛y1，y2，…，yn｝是L-半模M的2個子集.若對任意的xj，j∈可由y1，y2，…，yn線性表出且對任意的yi，i∈可由x1，x2，…，xm線性表出，則稱A和B等價，記作A～B.

引理1.1［14］設L是交換半環，A，B∈Mn（L）.若AB=In，則BA=In.

若無特別說明，在下文中總是假設L是交換半環.

2 強線性無關集的性質

本節將討論在有限生成L-半模M中強線性無關集的一些性質以及它與自由集之間的關系.首先，給出相關的定義.

定義2.1［13］在半環L中，a∈L是加法可消的當且僅當對任意的b，c∈L，由a+b=a+c知b=c.用K+（L）表示L中所有加法可消元組成的集合.若K+（L）=L，則稱L是加法可消半環.令V（L）=｛a∈L：存在b∈L，使得a+b=0｝.若a∈V（L），則稱a是加法可逆的.顯然V（L）?K+（L）.

令W（L）=｛a∈L：若b∈L，則存在元素r∈L，使得a+r=b或a=b+r｝.顯然W（L）是非空的，因為0∈W（L）.如果W（L）=L，那么稱L是yoked半環.

定義2.2［13］設0≠a∈L，若存在非零元b∈L使得ab=0，則稱a是左零因子，b是右零因子.若一個非零元既是左零因子又是右零因子，則稱之為零因子.沒有零因子的半環稱為整半環.

根據定義2.1和定義2.2，類似地可以定義.

定義2.3在半模M中，x∈M是加法可消的當且僅當對任意的y1，y2∈M，由x+y1=x+y2知y1=y2.用K+（M）表示M中所有加法可消元組成的集合.若K+（M）=M，則稱M是加法可消半模.令V（M）=｛x∈M：存在y∈M，使得x+y=0｝.對任意的0≠x∈M，若對任意的非零元b∈L使得b x≠0，則稱M是整半模.

定義2.6在L-半模M中，強線性無關的生成集稱為M的強線性無關基.

引理2.1［16］設L=〈L，+，·，0，1〉是半環，則：

1）對任意的a，b∈L，a+b∈V（L）當且僅當a，b∈V（L）；

2）對任意的a∈V（L），r∈L，則ra，ar∈V（L）.

根據定義1.5和定義2.4有如下結論.

命題2.1在L-半模M中，若｛x1，x2，…，xn｝是自由的，則｛x1，x2，…，xn｝是強線性無關的.

引理2.2［12］設M是有限生成自由半模，A是M的生成集且｜A｜=r（M），則A是自由基.

根據命題2.1和引理2.2有下面的結論成立.

推論2.1設M是有限生成自由半模且r（M）=n，則M中任意含有n個向量的基都是強線性無關的.

引理2.3設半環L中存在0≠a∈L是加法可逆的非零因子.M為L-半模，向量組x1，x2，…，xn，n≥2是M的向量組.

由0≠a∈L是加法可逆的非零因子和引理2.1知0≠ark∈V（L），其中k∈｛j，j+1，…，n｝.又由M是整半模和xj≠0知arj xj≠0，從而存在J1?｛j，…，n｝，J2?｛j，…，n｝且J1∩J2=?，使得

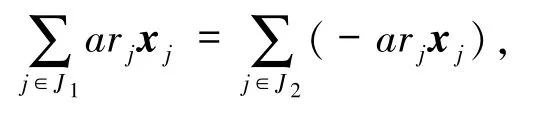
即x1，x2，…，xn半線性相關，矛盾.

定理2.4設L是yoked半環且存在0≠a∈L是加法可逆的非零因子，M是整的且加法可消的半模.｛x1，x2，…，xn｝是強線性無關的當且僅當｛x1，x2，…，xn｝是自由的.

證明由命題2.1知只需證明必要性即可.

必要性 對任意的α∈M，若

根據定理2.4和文獻［12］中的命題2.3有如下結論.

即A可由UA線性表出.從而UA是M的生成集.

2）要證UA是M的基，由1）知下面只需證UA是線性無關的即可.

假設UA是線性相關的，則存在i0∈s，j0∈n，使得

定理2.7設半環L滿足dim（V1（L））=1.設｛x1，x2，…，xm｝和｛y1，y2，…，ym｝是半模M上的兩組向量，滿足關系式（y1，y2，…，ym）=（x1，x2，…，xm）A，A∈Mm（L），其中｛x1，x2，…，xm｝是強線性無關的.若A是可逆的，則｛y1，y2，…，ym｝也是強線性無關的.

證明若y1，y2，…，ym是線性相關或半線性相關的，則存在2個不相交的非空指標集kj∈L，使得

由存在kj≠0且a11，a22，…，amm≠0（因為a11，a22，…，amm∈U（L））知存在kj ajj≠0，即x1，x2，…，xm是線性相關或半線性相關的，矛盾.故y1，y2，…，ym是強線性無關的.

3 強線性無關的基的性質

本節將討論強線性無關集的GM-rank并給出任意基都是強線性無關的等價刻畫.

定義3.1［17］設x1，x2，…，xn是M的向量組.若存在2個非空不交的指標集L，使得

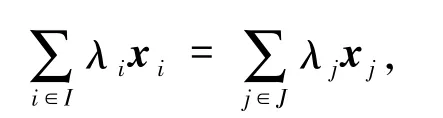
則稱向量組x1，x2，…，xn是Gondran-Minoux相關的，簡稱為GM-相關的；否則，稱向量組x1，x2，…，xn是GM-無關的.向量組x1，x2，…，xn的Gondron-Minoux rank是指向量組中強線性無關子集的最大基數，簡記為GM-rank.半模M的Gondran-Minoux rank=max｛k：k是M中GM-無關集的基數｝，簡記為GM-rank（M）.

注3.1由定義3.1、定義2.4和定義2.5知，若向量組x1，x2，…，xn是GM-無關的當且僅當x1，x2，…，xn是強線性無關的當且僅當x1，x2，…，xn的GM-rank等于n.若向量組x1，x2，…，xn是GM-相關的當且僅當x1，x2，…，xn是線性相關或半線性相關的.

由定義3.1知下列命題成立.

命題3.1設x1，x2，…，xm是半模M的向量組.若GM-rank（M）=n且m＞n，則x1，x2，…，xm是線性相關或半線性相關的.

命題3.2若x1，x2，…，xm是半模M的強線性無關的向量組，則GM-rank（M）≥m.

命題3.3若GM-rank（M）=n，則M中任意含有n+1個向量的向量組都是線性相關或半線性相關的.

命題3.4若M是含有強線性無關基的有限生成半模，則r（M）≤GM-rank（M）.

在下文中討論的半模都是含有強線性無關基的有限生成半模.

定理3.1半模M中任意強線性無關集的基數都不超過n當且僅當GM-rank（M）≤n.若M還滿足r（M）=n，則GM-rank（M）=n.

證明充分性和必要性根據定義3.1容易得到.

設x1，x2，…，xm是M的強線性無關的基，由r（M）=n知m≥n.又由M中任意強線性無關集的基數都不超過n知m≤n.故m=n，從而

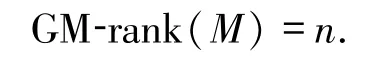
引理3.2若半模M的GM-rank（M）=r（M），則M的每組強線性無關基的基數都等于GM-rank（M）.

證明設GM-rank（M）=r（M）=n且x1，x2，…，xm是M的強線性無關基.由r（M）=n知m≥n.若m＞n，又由GM-rank（M）=n知x1，x2，…，xm是線性相關或半線性相關的，矛盾.因此，m=n.

引理3.3［18］在半模Vn（L）中每組基的基數都不會小于n.

推論3.1設在整半環L中存在0≠a∈V（L），則在半模Vn（L）中，每組強線性無關基的基數=GM-rank（Vn（L））=n.

定理3.4設在整半環L中存在0≠a∈V（L），若A=｛x1，x2，…，xn｝和B=｛y1，y2，…，ym｝是Vn（L）的2組基，則下列結論等價：

1）B是強線性無關的；

2）m=n；

3）B的GM-rank等于n.

證明由注3.1和推論3.1知只需證明2）?3）.

2）?3） 由于B是Vn（L）的一組基且含有n個向量，則B自由基，由命題2.1知B是強線性無關的，故B的GM-rank等于n.

由定理3.4有如下結論.

推論3.2設在整半環L中存在0≠a∈V（L），則下列結論等價：

1）Vn（L）中的每組基都是強線性無關的；

2）Vn（L）的每組基都有相同的基數.

定義3.2［19］設矩陣A∈Mm×n（L），A的列向量組的GM-rank記作GMc（A），A的行向量組的GM-rank記作GMr（A）.當GMc（A）=GMr（A）時稱為A的GM-rank，記作GM（A）.

注3.2由定義3.2知GM（A）≤min｛m，n｝.

定理3.5設M是整半模且x1，x2，…，xn和y1，y2，…，ym是M的2組向量，其中x1，x2，…，xn是強線性無關的，滿足關系式（y1，y2，…，ym）=（x1，x2，…，xn）A，A=（aij）∈Mn×m（L）.若存在0≠a∈L是加法可逆的非零因子且GMc（A）＜m，則y1，y2，…，ym是線性相關或半線性相關的.

證明設

則方程（9）可以等價的寫成

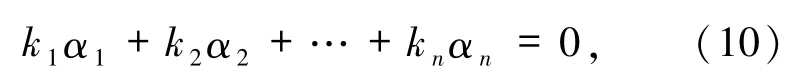
其中α1，α2，…，αn是A的列向量組.由GMc（A）=m知α1，α2，…，αn是線性相關或半線性相關的.又由引理2.3知在方程（10）中存在ki≠0，i∈n，從而x1，x2，…，xn是線性相關或半線性相關的，矛盾.同理，可由m＞n得出矛盾，故m=n.

4 結論

在本文中，在有限生成半模上給出了自由集和強線性無關集兩者之間的關系.其次，給出了交換半環上有限生成半模中強線性無關基和半模M的GM-rank之間的關系，然而對于含有強線性無關基的有限生成半模的基數問題仍沒有解決.