矩和矩不變量在圖像處理和模式識別中的應用綜述

舒華忠

（東南大學 計算機學院 影像科學與技術實驗室，江蘇 南京210096）

從基礎學科的生物學、醫學、化學、地質學等，到工程領域的機器人控制、遙感、增強虛擬現實等，灰度圖像和彩色圖像都起著非常重要的作用.所有這些領域都需要通過某種方法來提取、量化和解釋它們所包含的信息，這些方法通常涉及圖像處理.

盡管圖像分析的方法依賴于具體的應用，但在許多問題中，目標不變量的描述對于物體的檢測、配準、檢索以及更廣泛的模式識別都具有重要的意義.它們首先要處理圖像的幾何變換，如平移、縮放和旋轉，甚至更一般的情況如仿射變換.圖像模糊是面臨的另一個問題，模糊可以由對焦錯誤、對象或相機運動造成.研究針對圖像幾何變換和模糊的不變量，長期以來吸引著學者的關注.

一類流行的不變特征構造方法是基于矩函數.正如Ghorbel等［1-2］指出的，圖像描述符評估的最重要特性是：1）對某些幾何變換的不變性；2）對噪聲、模糊、非剛性和小局部變形的穩定性；3）完備性.本文的一個目的是綜述模式識別中矩不變量的研究現狀.由于矩的計算復雜度高，其快速計算也有諸多的研究，本文將對此做一比較全面的介紹.

彩色圖像在實際中的應用起來越多，傳統處理彩色圖像的方法有2類：一是將其轉化為灰度圖像，這類方法的不足是丟失了顏色信息；另一類是對彩色圖像的每個通道分別進行處理，然后將輸出結果進行組合，這類方法沒有考慮3個通道的內在關聯.要克服傳統方法存在的不足，需要找到一種途徑，它能夠以一種整體的方式同時處理彩色圖像的每個像素.本文的另一個目的是介紹基于四元數矩的彩色圖像處理方法.有關矩的綜述文章和專著，可參見文獻［3-10］.

本文的組織結構如下：第1節介紹灰度圖像矩的定義、不變量構造方法以及精確和快速計算；第2節闡述彩色圖像四元數矩的有關理論；最后一節是總結.

1 灰度圖像矩

1.1 灰度圖像矩的定義對于密度函數為f（x，y）的一幅二維灰度圖像，其矩函數的一般定義形式為

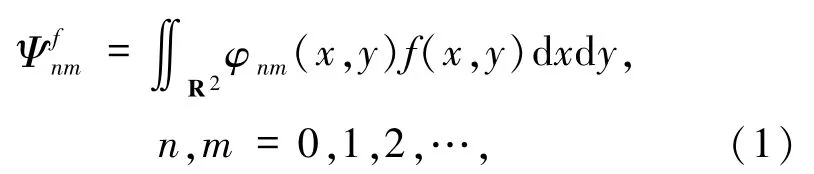
式中的φnm（x，y）稱為基函數，其選擇決定了矩的類型.

1.1.1 幾何矩 幾何矩是將圖像映射至單項式，即φnm（x，y）=xn ym，（n+m）階的幾何矩為

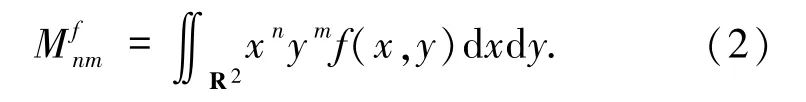
幾何矩在圖像分析和模式識別中應用最為廣泛，這主要得益于它的簡單性、不變性，以及低階矩所具有的幾何意義.實際上，零階矩M00代表灰度圖像的質量，一階矩（M10，M01）表示質心的位置，二階矩（M20，M11，M02）可用于表征圖像橢圓的特性［3］.

1.1.2 復數矩 復數矩對應的基函數為

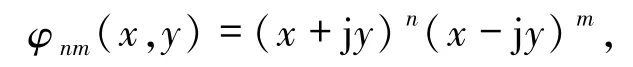
這里j為虛數符號，（n+m）階復數矩的定義［11］為

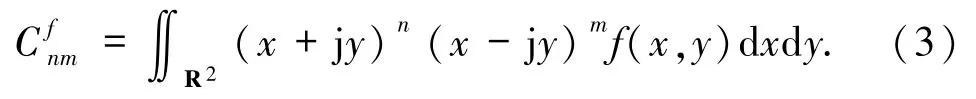
上式可以轉化為極坐標下的形式

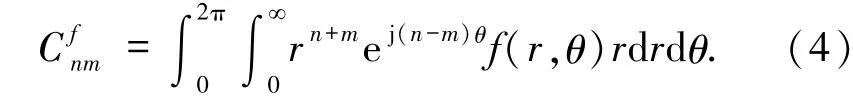
（4）式定義的矩也稱為徑向矩.

當圖像沿逆時針旋轉角度φ，即

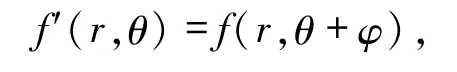
則旋轉前后圖像的復數矩具有如下關系

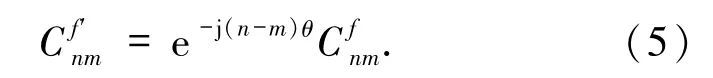
1.1.3 正交矩 如前所述，幾何矩是圖像f（x，y）在單項式xn ym上的投影.然而，基集｛xn ym｝不是正交的.因此，就信息冗余而言，幾何矩不是最優的.此外，由于缺乏正交性，使得基于幾何矩的圖像重建是一個病態問題.復數矩也具有同樣的問題.為了克服這些不足，Teaguem［12］使用連續正交多項式（如Legendre和Zernike多項式）定義一類新的正交矩.之后，學者們又引入離散正交矩：Tchebichef矩［13］、Krawtchouk矩［14］、Racah矩［15］和dual-Hahn矩［16］等.下面分別予以介紹.

（a）連續正交矩（Legendre矩）.Legendre矩的基函數為φnm（x，y）=Pn（x）Pm（y），其中Pn（x）為n階Legendre多項式，其定義如下

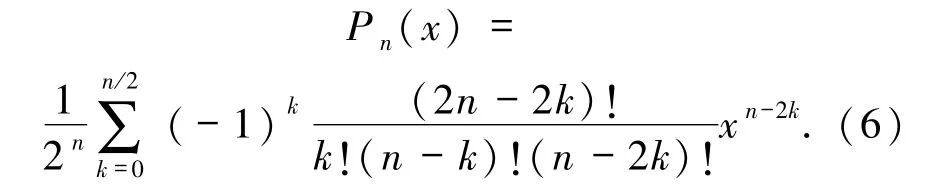
二維灰度圖像f（x，y）的（n+m）階Legendre矩由下式［12］給出因

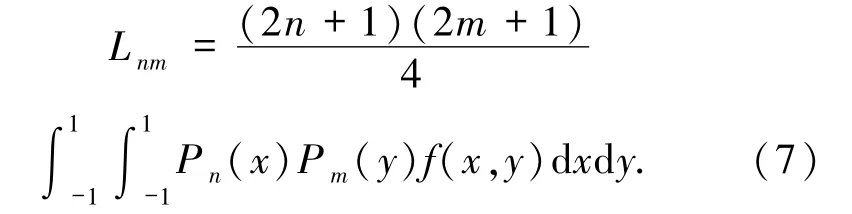
為Legendre多項式在區間［-1，1］內正交，所以圖像f（x，y）可由下式重建

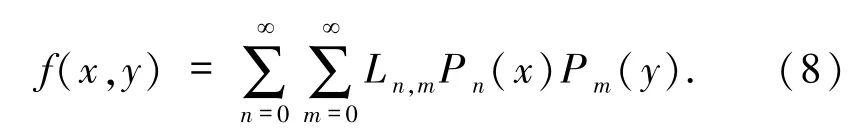
Zernike矩.對于一幅二維圖像f（r，θ），其Zernike矩Znm（n表示階數，m為重復度）的定義［12］為

Zernike矩具有與復數矩類似的性質，也就是說，若f′（r，θ）=f（r，θ+φ），則旋轉前后圖像的Zernike矩具有如下關系

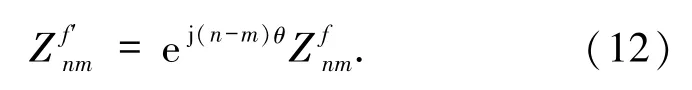
對上式兩端取模，則Zernike矩的模對圖像旋轉具有不變性.得益于這一性質，Zernike矩在模式識別中得到廣泛的應用.其他定義在單位圓內的正交矩還有偽Zernike矩［17］、Chebyshev-Fourier矩［18］和廣義的偽Zernike矩［19］等，感興趣的讀者可閱讀相關的文獻.

（b）離散正交矩.連續正交矩在圖像分析和模式識別中獲得了廣泛應用，但存在以下不足：1）它們都定義在特定區域，需要對圖像做相應的變換；2）實際計算中，需要對積分進行離散，會帶來離散化誤差；3）使用反變換重建圖像時，需要進行截斷，存在截斷誤差.為解決上述問題，學者們于21世紀初引入離散正交矩（Tchebichef矩）.

對于一幅N×N的數字圖像f（x，y），其（n+m）階Tchebichef矩的定義［13］為

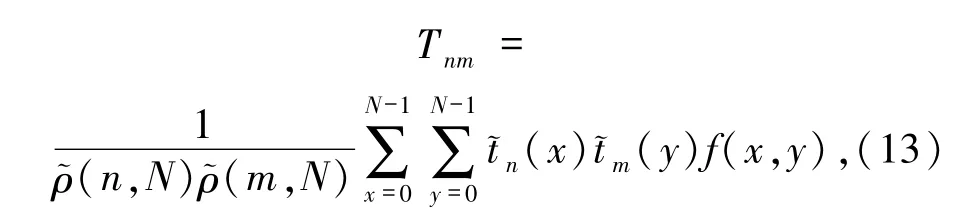
這里~（x）為歸一化的n階Tchebichef多項式，滿足如下正交性

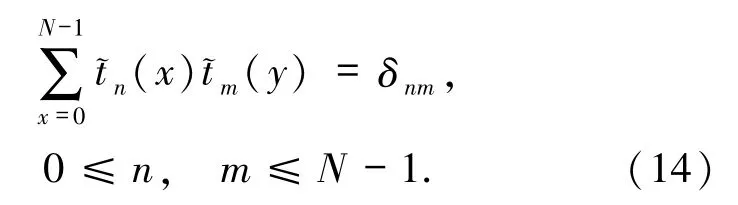
（13）式對應的反變換為

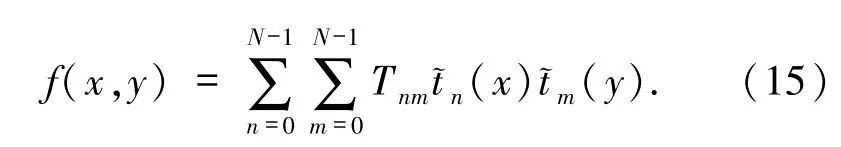
其他類型的離散正交矩還包括Krawtchouk矩、Racah矩和dual-Hahn矩等，限于篇幅，本文不一一介紹.

1.2 矩不變量構造方法目標不變量的構造在模式識別中具有十分重要的意義.矩函數在圖像處理和模式識別領域獲得廣泛應用的一個重要原因是因為它們具有一些良好的性能，如對幾何變換、圖像模糊的不變性.下面分別予以介紹.

1.2.1 幾何不變量 在過去的幾十年，矩不變量的構造方法得到了廣泛的研究.這些方法可分為3類：1）歸一化技術；2）間接方法；3）直接方法.眾所周知，歸一化過程可用來實現不變性.然而，這樣的處理會帶來不精確性，因為圖像的歸一化需要重新采樣和量化.間接法利用幾何矩或復數矩來實現不變性，但其時間開銷較大.為了提高計算精度和效率，文獻中報道了許多直接算法.

Hu［20］在20世紀60年代提出了構造矩不變量的開創性工作.基于不變代數理論，Hu推導了7個與圖像尺度、平移和旋轉無關的矩不變量，這些不變量是零至三階幾何中心矩的線性組合.Sadjadi等［21］將Hu的不變矩推廣至三維.Liu等［22］提出了構造不變矩的一般框架.Suk等［23］構造了一組針對投影變換的不變矩.前文介紹的復數矩以及定義在單位圓內的正交矩都具有旋轉不變性.

正交矩的尺度不變性和平移不變性問題也曾經是一個研究熱點.Chong等［24］提出了一種建立偽Zernike矩尺度不變量集的方法，該方法直接基于偽Zernike多項式的性質；文獻［25］使用類似的方法來構造Legendre矩的平移和縮放不變量；文獻［26］還研究了Zernike矩的平移不變性.Zhu等［27］提出了一種構造Tchebichef矩的尺度和平移不變量的方法.結果表明，文獻［24-27］中提出的方法比傳統的圖像歸一化方法和間接方法具有更好的性能.

矩不變量的完備性問題也引起了學者的關注.如果一組不變描述子滿足以下性質，則稱其為完備的：2個物體具有相同的形狀當且僅當它們具有相同的不變描述子集.Flusser［28-29］通過對復數矩進行歸一化，構造了一個完整并且獨立的旋轉不變量集合.Ghorbel等［1］研究了利用復數矩的線性組合構造相似不變量（平移、旋轉和縮放）完備集合.Zhang等［30］基于Fourier-Mellin矩，提出了構造完備不變量集合的一種通用方法，該方法很容易推廣至其他矩.

仿射變換較平移、縮放和旋轉具有更一般的形式，仿射不變矩也因此具有更好的性能.Reiss［31］以及Flusser等［32］分別基于代數不變量和張量理論推導了仿射不變矩.Suk等［33］使用圖方法構造仿射不變矩.Liu等［34］提出了一種自動生成仿射不變量的方法.歸一化是另一種構造不變矩的方法.仿射歸一化方法最早由Rothe等［35］提出.在他們的工作中，使用了2種不同的仿射分解：第一種分解方法包括2種傾斜，各向異性縮放和旋轉；第二分解方法由2個傾斜和各向異性縮放組成.Zhang等［36］對這些仿射分解進行了研究，指出這2種分解都會導致一些歧義，并提出了進一步的改進.Pei等［37］對非對稱物體提出了仿射歸一化方法；Suk等［38］對對稱物體進行了處理.Shen等［39］利用廣義復矩分析了它們在對稱物體識別中的性能.Zhang等［40］采用Legendre矩，提出一種構造具有正交特性的仿射不變量方法.

1.2.2 模糊不變量 由于成像系統大多是不完善的，并且環境條件隨著時間的推移而變化，因此獲取的圖像往往是真實場景的退化版本.在實際應用中，面臨的一類重要的退化是圖像模糊，它可以由衍射、透鏡像差、錯誤聚焦和大氣湍流引起.模糊通常可以描述為一個未知的原始圖像與空間不變的點擴散函數的卷積，即

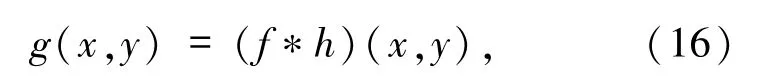
其中，g（x，y）是實際獲取的圖像，也稱為退化圖像，f（x，y）為理想圖像，h（x，y）是成像系統的點擴散函數，它通常是未知的，*表示線性卷積.

在模式識別中，對模糊圖像的處理，有2類方法已被廣泛研究：一種是通過兩步方法識別物體，即先恢復理想圖像，然后對后者應用識別方法；另一種是通過設計一個沒有模糊效應的一步解決方案.在前一種情況下，由于點擴散函數通常是未知的，因此圖像復原是一個病態問題，需要通過先驗知識做一些額外假設.在后一種情況下，找到一組不受模糊影響的不變量是關鍵.

Flusser等［41］在這一領域做了開創性的工作，他們基于點擴散函數具有中心對稱的假設，使用幾何矩構造了針對圖像模糊的不變量.這些不變量被成功應用于衛星模式識別、模糊數字和字符識別.Flusser等［42］進一步引入了針對圖像模糊和旋轉變換的組合不變量，在此基礎上，Suk等［43］還構造了一組對仿射變換和模糊的組合不變量.模糊不變量還被進一步推廣至任意維的情況［44-45］.由于正交矩在信息冗余方面優于非正交矩，并且對噪聲具有更強的魯棒性，Zhang等［46］采用Legendre矩，構造了針對圖像模糊的不變量，較之前的方法具有更好的性能.Chen等［47］基于Zernike矩，提出了對相似變換和模糊的組合不變量.

1.3 矩的精確和快速計算方法

1.3.1 矩的精確計算 大多數矩函數是以連續形式定義的.以二維圖像為例，（1）式中的二重積分通常用二重求和來近似.為了提高精度，Liao等［48］針對幾何矩和Legendre矩常用的近似公式，提出了改進，文獻［49］還將這一策略應用于Zernike矩.Xin等［50］提出了一種在極坐標系下高精度計算Zernike矩的方法.Kotoulas等［51］使用分段多項式插值來獲得更高精確的幾何矩.Jacob等［52］提出了一種小波矩的精確計算方法.Sheynin等［53］提出了一種計算由樣條曲線邊界描述的二維物體幾何矩的方法.

1.3.2 矩的快速計算方法 文獻中已經報道了許多算法.在早期的工作中，Hatamian［54］對大小為N×N的二維圖像使用了只需要O（N2）加法的因果空間濾波器.Zakaria等［55］提出了二值圖像的delta方法，這種方法適用于由y線表示的圖像.Dai等［56］和Li［57］對其進行了改進.另一些快速算法利用了物體的邊界角點［58-60］，這類方法僅適用于二值圖像，需要O（K）加法和乘法，其中K表示角點的數目.通過擴展Jiang的算法，Li［61］提出了一種計算多面體三維圖像幾何矩的快速算法.Sheynin等［62］進一步給出了顯式計算公式.Tuzikov等［63］提出了一種計算任意維多面體表面矩的通用方法.

另一類快速算法是基于格林公式將二重積分轉化為圍線積分，以此減少運算量.Li等［64］描述了一種僅需要O（N）次加法和乘法的快速方法.他們的方法雖然有效，但精度不夠高.使用離散的格林定理，Philips［65］提出幾何矩的一種精確計算方法，但效率略低.Yang等［66］采用精確的離散格林公式，提出一種灰度圖像幾何矩的高效算法；文獻［67］將該方法推廣至三維.Spiliotis等［68］提出一種二值圖像塊表示方法，以此為基礎研究了矩的快速計算；Flusser［69］對其進行了改進；Chung等［70］將相關方法推廣至灰度圖像.

上述算法大多是針對級聯系統設計的，Chen［71］首次提出了一種適合于并行實現的矩的計算方法.Liu等［72］針對灰度圖像，提出一種僅需要加法運算就可以獲得矩值的方法，并且可以并行實現.

針對正交矩的快速計算問題，Mukundan等［73］首先使用格林公式，然后采用迭代方法計算Legendre多項式.Shu等［74］提出了Legendre矩的改進方法，有效提高了精度和計算效率，文獻［75］進一步擴展到多面體的Legendre矩計算.Zhou等［76］研究了由y線表示圖像的Legendre矩計算問題.Zernike矩的快速計算問題也得到了廣泛的研究.Mukundan等［73］提出了一種從正方形到圓形的圖像變換來簡化計算.Belkasim等［77］使用Zernike多項式的徑向和角度展開來加速算法.采用Zernike多項式的遞歸性質，Gu等［78］研究了一種有效的迭代方法.Wee等［79］提出了一種混合算法來計算Zernike矩.Hwang等［80］利用Zernike基函數的對稱性，提出了一種快速準確的計算方法.Chong等［81］研究了一種p-遞歸方法，該方法使用低階多項式的組合來推導具有相同重復度q的高階多項式，以提高計算效率.

離散正交矩的快速計算也受到了人們的關注.使用Tchebichef多項式的對稱性質，Mukundan［82］研究了Tchebichef矩的快速計算方法.利用Clenshaw遞推公式，Wang等［83］推導了一種適合VLSI實現的Tchebichef矩的遞推算法.Shu等［84］采用圖像塊表示方法，提出了一種有效計算Tchebichef矩的方法.

2 四元數矩

2.1 彩色圖像四元數矩的定義

2.1.1 四元數及基于四元數的彩色圖像表示 四元數是數學家Hamilton［85］在1843年提出的，它是傳統復數的推廣.四元數有1個實部和3個虛部，即

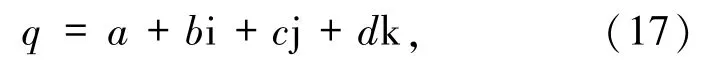
其中，a，b，c，d∈R，i、j、k是3個純單位虛數且滿足如下關系

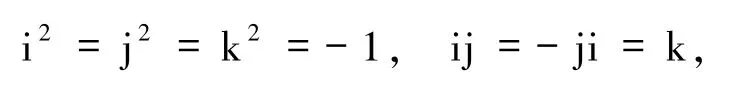
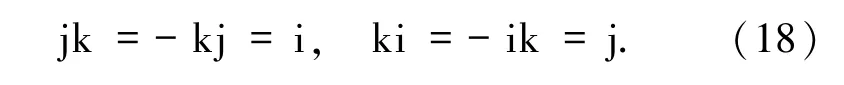
若實部a=0，q稱為純四元數，四元數的共軛和模分別由下式定義：

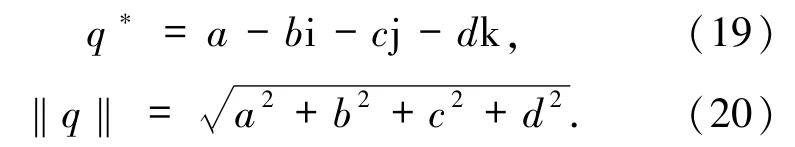
若f（x，y）為一幅彩色圖像，則它的每個像素可用四元數表示為

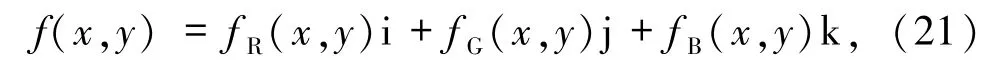
其中，fR（x，y）、fG（x，y）和fB（x，y）分別為每個像素的紅、綠和藍3個通道的值.

2.1.2 四元數矩及其快速計算方法 彩色圖像的四元數矩通常都定義在極坐標內，由（18）式可知，四元數的乘法不具有交換性，因此相應的矩具有2種不同和形式：左邊（L）和右邊（R），以下用上標標識.給定一幅彩色圖像f（r，θ），它的右邊四元數矩的一般形式為

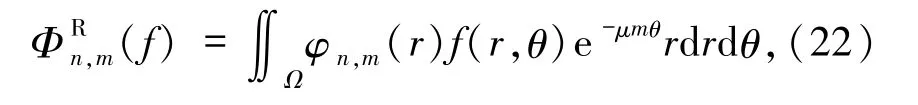
其中φn，m（r）為一實值多項式.

表1列舉了若干常用的多項式類型，Ω是圖像定義域，μ是一個單位純四元數，它的一種常用選擇方式為

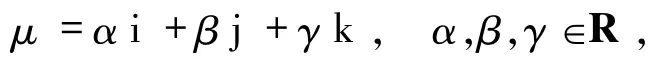
且‖μ‖=1.

對于一幅尺N×N的數字圖像［86］，（22）式可用下式近似得到

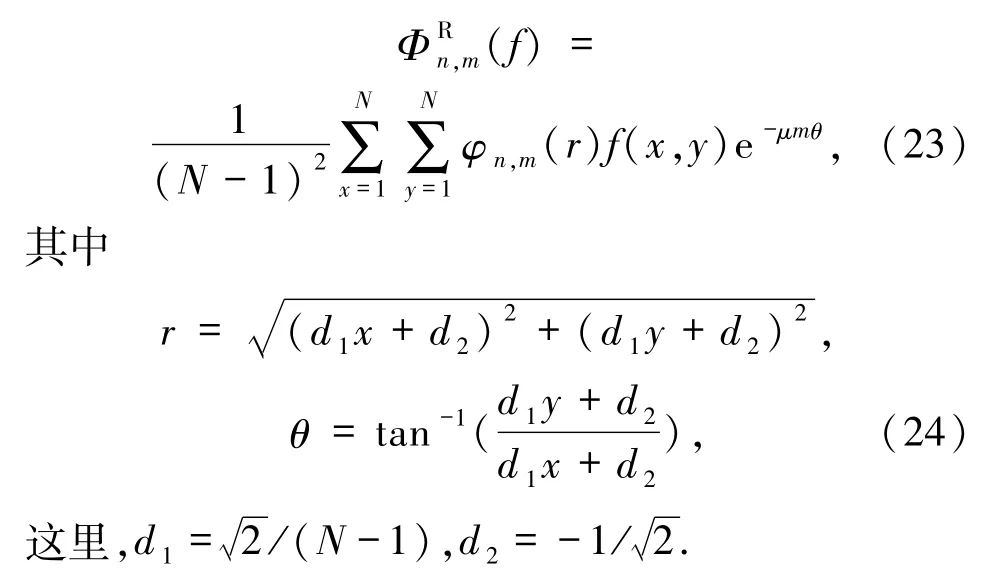
需要指出的是，表1中列舉了7種不同的徑向函數，其中前3種為非正交函數，后4種為正交函數.如果徑向多項式是正交的，則圖像f（r，θ）可通過下述反變換重建

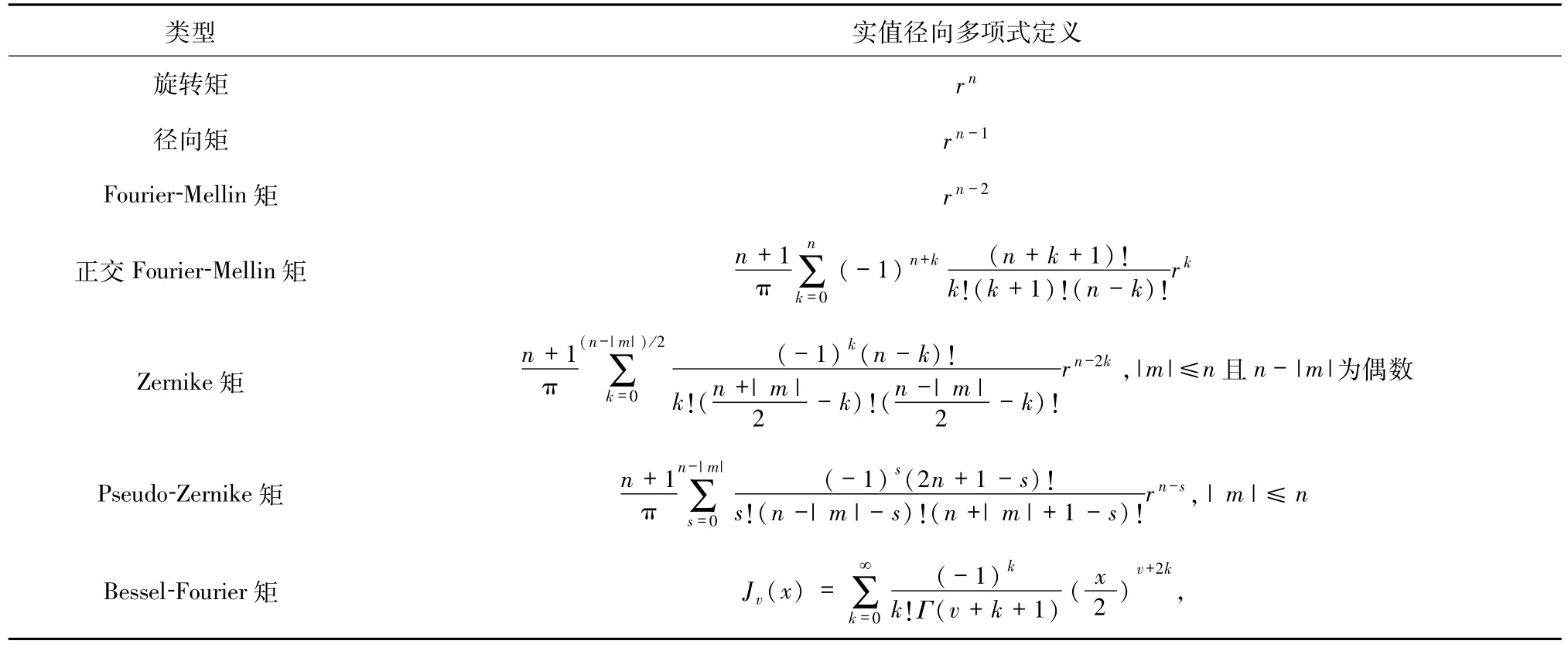
表1 四元數矩徑向多項式的定義Tab.1 Definition of radial polynomials used in the quaternion moments

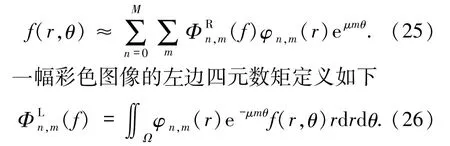
對應的反變換為

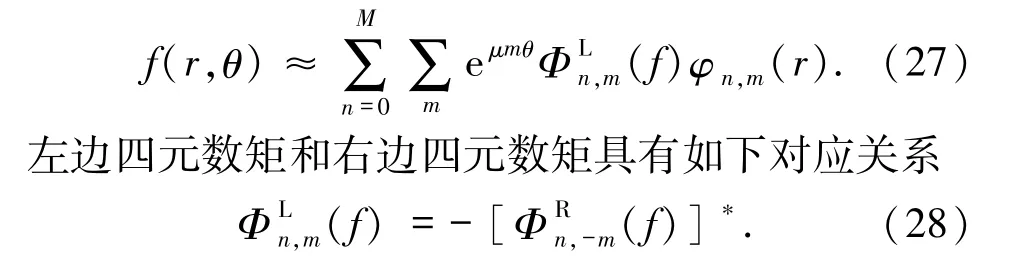
后文將會介紹，借助這個性質，可以構造四元數矩的旋轉不變量.

較之灰度圖像矩，四元數矩的計算復雜度更高，因此需要尋找有效的計算方法.Chen等［86］提出一種降低計算復雜度的方法，簡要介紹如下.

考慮μ=αi+βj+γk的情況，則可將（23）式表示為

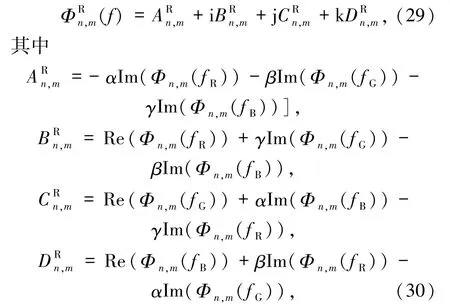
這里，Φn，m（fR）、Φn，m（fG）和Φn，m（fB）分別表紅、綠和藍3個通道的矩，即與傳統的灰度圖像矩一致；Re（x）傳統復數x的實部，Im（x）為虛部.

采用上述方法，算術運算量可減少一半，更重要的是，對每個通道的矩，可以通過使用灰度圖像矩已有的高效計算方法，進一步提高計算效率.

2.2 四元數矩的不變量構造物體對平移、縮放和旋轉等幾何變換的不變性，是模式識別中的一個關鍵特征.本節介紹如何構造一組針對幾何變換的四元數矩不變量.以四元數Zernike矩為例來進行說明.

Guo等［87］推導了一組關于平移、縮放和旋轉變換的不變量.然而，它們的旋轉不變性是通過對四元數矩取模來實現的，這不僅導致了相位信息的丟失，而且只提供了一個實值不變量.Chen等［88］提出了一種構造四元數不變矩集的通用方法，并將其應用于彩色目標識別和模板匹配.下面對這一方法做一介紹.

（a）平移不變性.Suk等［89］采用下式定義了彩色圖像的質心（xC，yC）

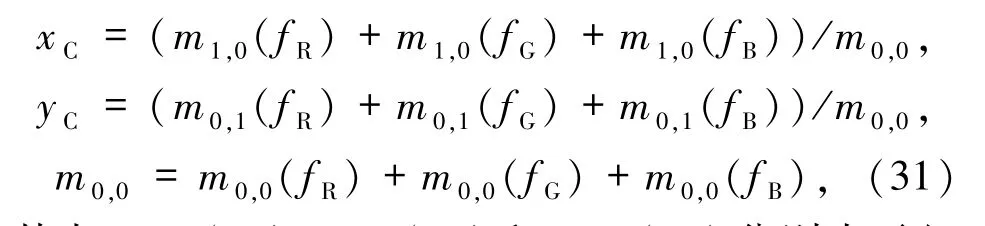
其中，m0，0（fR）、m1，0（fR）和m0，1（fR）分別表示紅色（R）通道的零階和一階幾何矩，下標G和B分別代表綠色和藍色通道.

將坐標軸原點置于（xC，yC），則定義的中心矩具有平移不變性.

（b）旋轉不變性.設f′（r，θ）=f（r，θ+φ），這里φ表示圖像的旋轉角度，則有

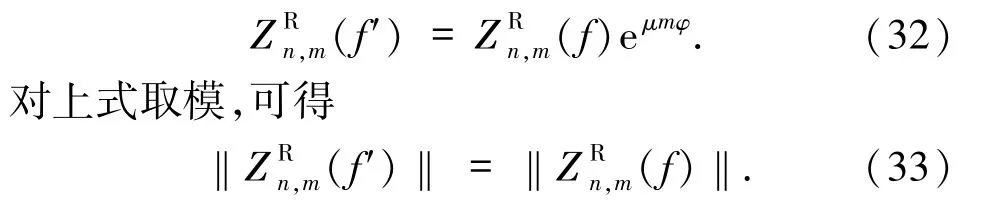
上式表明，四元數矩的模對圖像旋轉具有不變性，但取模丟失了相位信息.為此，提出一種新的方法得到旋轉不變量.將上述過程運用于左邊四元數矩，可以得到

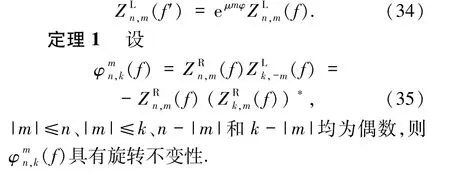
（c）縮放不變性.記f″為圖像f縮放后的圖像，縮放因子為λ，即f″（r，θ）=f（r/λ，θ），則有以下定理.

定理2設

定理1至3的證明感興趣的讀者可參閱文獻［88］.

如前所述，平移不變性可通過將坐標原點置于圖像的質心得到，因此可以獲得四元數矩針對平移、旋轉和縮放的不變量.上面介紹的方法可以很容易推廣到其他類型的四元數矩.限于篇幅，此處不再贅述.

需要指出的是，Shao等［90］引入了四元數Bessel-Fourier矩，將其相位作為彩色圖像的特征描述子，用于彩色圖像的物體識別，獲得了很高的識別率.限于篇幅原因，本文不做詳細介紹.

3 總結

本文在介紹灰度圖像矩和彩色圖像四元數矩的概念之后，全面闡述了矩的不變量構造方法，為了能夠解決實際中需要實時或近乎實時處理的問題，詳細介紹了矩的快速算法.需要指出的是，不變矩只能用于解決部分計算機視覺中的問題，如何能夠讓這一曾經被廣泛應用的概念煥發新的活力，需要研究者們付出更多的努力.