基于FUNWAVE-TVD模型的岸礁次重力波數值模擬

馮衛兵，華偉豪,2，張 俞,2

(1.河海大學港口海岸與近海工程學院，江蘇 南京 210098； 2.河海大學海岸災害及防護教育部重點實驗室，江蘇 南京 210098)

岸礁海岸是一種典型的珊瑚礁海岸，主要分布于南北回歸線之間的熱帶海洋，在我國的海南島和雷州半島沿海分布廣泛。岸礁地形主要由陡峭的礁前斜坡、水深較淺且相對平坦的礁坪及礁后斜坡組成，礁前斜坡與礁坪連接處為礁緣，發育成熟的礁坪寬度通常幾百米至幾千米不等。波浪是影響和塑造岸礁海岸最重要的海洋動力因素之一[1]，當深海波浪傳至礁前斜坡時，由于該區域內水深急劇變化，波浪經淺水變形在礁緣附近破碎并損耗大量能量，破碎后波浪繼續沿礁坪向岸傳播，此過程中受礁坪底摩阻的影響波能進一步耗散，最終到達岸線處的高頻短波能量很小，此處波浪動力一般由頻率較低的次重力波主導[2]。次重力波頻率位于0.004～0.04 Hz之間，其生成機制主要包括兩種：(a)Longuet-Higgins等[3]提出的約束波機制，即由波浪差頻作用形成的伴隨波群傳播的二階次諧波，其幅值在向岸入射過程中隨水深減小幅值逐漸增長，并在短波破碎后從波群釋放成為自由長波[4]；(b)Symonds等[5]提出的破碎點移動機制，入射波高的變化導致破碎點在垂岸方向振蕩，隨時間變化的輻射應力梯度在破碎帶內生成向岸與離岸的自由長波。次重力波是岸礁海岸的形成、發育和演變的主要動力之一，因此研究岸礁海岸的次重力波的生成與傳播規律具有非常重要的意義。

早期對于岸礁海岸的波浪研究以現場觀測和物理模型試驗為主，隨著計算機技術的發展，數值模擬成為研究該問題的主要方法之一。van Dongeren等[6]采用基于非線性淺水方程的Xbeach模型分析了帶有潟湖的Ningaloo岸礁上的次重力波運動；Ma等[7]采用基于N-S方程的非靜壓模型NHWAVE研究了次重力波波高及能量在岸礁地形的沿程變化；Pelez-Zapata等[8]采用非靜壓模型SWASH研究了短波與次重力波在礁后斜坡的爬高。由于Boussinesq模型兼顧了計算效率與精度，可模擬波浪的非線性與色散性，因此近年來被廣泛應用于珊瑚礁地形的波浪數值模擬中，如Nwogu等[9]采用任意水深層Boussinesq模型捕捉到了礁坪末端低頻波的一階共振放大現象；Su等[10]將激波捕捉法應用于完全非線性的Boussinesq模型FUNWAVE-TVD,研究了岸礁底摩阻與礁坪水位等對次重力波的影響，隨后諸裕良等[11]應用該模型模擬了不規則波在岸礁上的傳播過程，分析了礁坪寬度、礁后斜坡坡度對礁坪傳遞波高和爬高的影響；Ning等[12]進一步總結了水位與地形等條件對次重力波爬高的影響；Yao等[13]利用高階非線性Boussinesq模型結合現場觀測資料研究了實際尺度下岸礁地形的次重力波的生成并分析了其在礁坪上的激發模態。

從已有研究來看，以往利用Boussinesq模型對岸礁地形次重力波的數值模擬研究多涉及波高與波浪爬高，對非線性能量傳遞過程涉及較少；考慮到次重力波存在多種生成機制及其較高的反射系數，采用相關性分析區分各重力波分量在時域上的傳播過程對研究岸礁地形的次重力波運動尤為重要。本文在岸礁地形不規則波物理模型試驗數據驗證的基礎上，采用FUNWAVE-TVD模型3.4版本分析了次重力波在岸礁地形的生成、傳播及相關的能量演變過程。

1 數值模型簡介

FUNWAVE-TVD模型是特拉華大學開發的完全非線性的Boussinesq數值模型，該模型基于由Chen[14]建立的控制方程：

ηt+?·M=0

(1)

uα,t+(uα·?)uα+g?h+V1+V2+V3+Rf+Rs=0

(2)

數值模型控制方程采用有限體積法和有限差分法進行離散，對色散項使用有限差分法處理，其他項使用有限體積法求解；時間積分采用較為穩定的Runge-Kutta法確定自適應時間步長，利用CFL準則保證計算收斂；計算過程結合HLL近似黎曼求解器計算數值通量、高階MUSCL-TVD法求解界面通量。

FUNWAVE-TVD模型在模擬波浪破碎過程中可采用激波捕捉法將波高水深比作為判斷波浪破碎的閾值，通過關閉色散項將方程退化為非線性淺水方程模擬波浪破碎過程，但其模擬結果可能造成對礁坪上次重力波頻段波能的顯著低估[10,12]。本文采用改進后的在控制方程中添加人工渦旋黏性項的方法[15]模擬波浪破碎時能量的耗散，人工黏性項Rbx表達式為

(3)

其中ν=Bδb2(h+η)ηtP=(h+η)u

式中：ν——黏性系數；P——水平動量流；δb——混合長度系數，δb=1.2；u——水質點水平速度；B——黏性項啟動系數，根據自由波面對時間的偏導數ηt控制該項開啟或關閉，表達式為

(4)

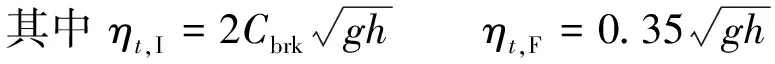
式中：Cbrk——破碎參數；ηt，I——破碎起始閾值，當ηt≥ηt，I時，波浪破碎開始；ηt，F——破碎終止閾值，當ηt<ηt，F時黏性項為0，破碎終止。

FUNWAVE-TVD模型可對固邊界、動邊界和吸收邊界進行模擬。模型固邊界時令固壁處法向速度、波面法向梯度及切向速度法向梯度都為0；動邊界采用干濕網格法進行處理；吸收邊界通過設置海綿層實現，海綿層采用Larsen等[16]直接衰減型與摩阻型的組合，前者令海綿層內變量φ(即u,η)在每個時間步長直接發生衰減：

φ=φ/Cs

(5)

式中：Cs——衰減系數；n——網格數；αs、γs——參數，用于控制衰減系數隨網格的變化率。摩阻型海綿層直接采用模型中的底摩阻項加以處理，數值模型中通過在動量方程中添加底摩阻項的方法模擬底摩阻的影響：

Rf=-Cduα|uα|

(6)

式中：Cd——底摩阻系數。

2 模型驗證

2.1 物理模型試驗簡介

為了驗證FUNWAVE-TVD模型對岸礁地形波浪傳播數值模擬的適應性，采用Demirbilek等[17]在密歇根大學進行的風浪水槽物理模型試驗數據驗證模型。該試驗在長35 m、寬0.7 m、深1.6 m的水槽中進行，如圖1所示，x為距礁緣水平距離，地形剖面由復合坡度的礁前斜坡、4.8 m寬的礁坪和1∶12的礁后斜坡組成，礁坪對應z=0 m高程，礁坪與槽底的垂直距離為0.5 m，岸礁模型表面為相對光滑的PVC材質。造波機距礁前斜坡坡腳15.5 m，入射波基于隨機相位的JONSWAP譜生成，譜峰增強因子為3.3。自造波機向岸沿程8個測點(G1～G8)處布置的波高儀用于記錄波面時間序列，測點距礁緣水平距離分別為-5.91 m、-5.72 m、-5.39 m、-1.12 m、-0.58 m、0 m、2.17 m和4.34 m位置，采樣頻率均為20 Hz。

圖1 物理模型試驗設置Fig.1 Experiment setup of physical model

2.2 參數設置

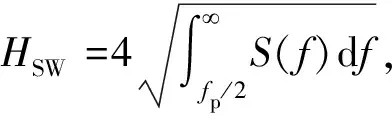
表1 入射波工況

(7)

式中：N——測點數；xm——試驗值；xp——模擬值。I越接近1說明模型精度越高。

2.3 參數敏感性分析

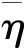
取破碎參數Cbrk=0.40、0.55、0.70分別進行數值模擬計算，結果如圖2所示。3種工況下短波有效波高的模擬值與試驗值吻合均較為良好，譜峰周期較小時短波傳至礁前斜坡時已開始耗散且無顯著的淺化成長。次重力波有效波高在礁前斜坡有所增長，在礁坪上呈波動狀，并隨入射波譜峰周期增大而增大。模型對礁前常水深處次重力波波高有所高估，但礁坪上模擬值與試驗值吻合較好，模型較合理地模擬了次重力波波高的沿程變化。Test45中，時均水位的模擬值與試驗值吻合較好，其余兩種工況下模擬值較試驗值偏大。破碎參數取不同值時，礁坪上次重力波有效波高有所變化，但對模擬結果總體影響較小。

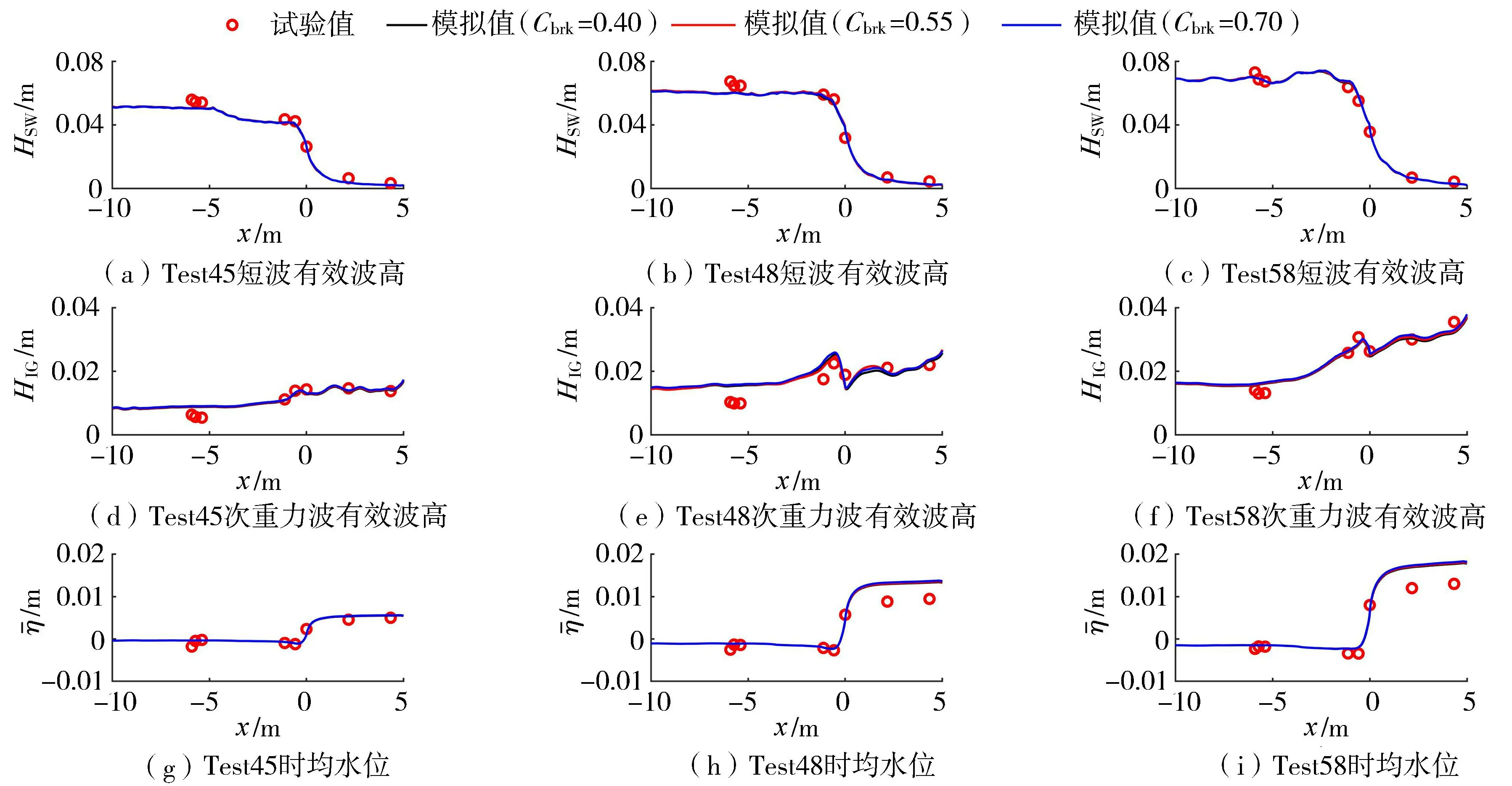
圖2 不同破碎參數條件下參數試驗值與模擬值空間分布對比Fig.2 Spatial distribution comparison of measured and predicted results with different breaking parameters

取底摩阻系數Cd=0.001、0.005、0.010、0.015分別進行數值模擬計算，結果如圖3所示。底摩阻系數對短波影響較小，礁坪上短波有效波高隨底摩阻系數增大有輕微下降；次重力波有效波高對底摩阻系數變化敏感，隨底摩阻系數增大而減小，由于礁前常水深處部分次重力波能量來自礁后斜坡反射的次重力波，因此此處波高也受底摩阻系數影響較大；時均水位對底摩阻系數變化基本不敏感。總體而言，底摩阻系數取0.005或0.010時岸礁上次重力波有效波高模擬值與試驗值吻合更好。

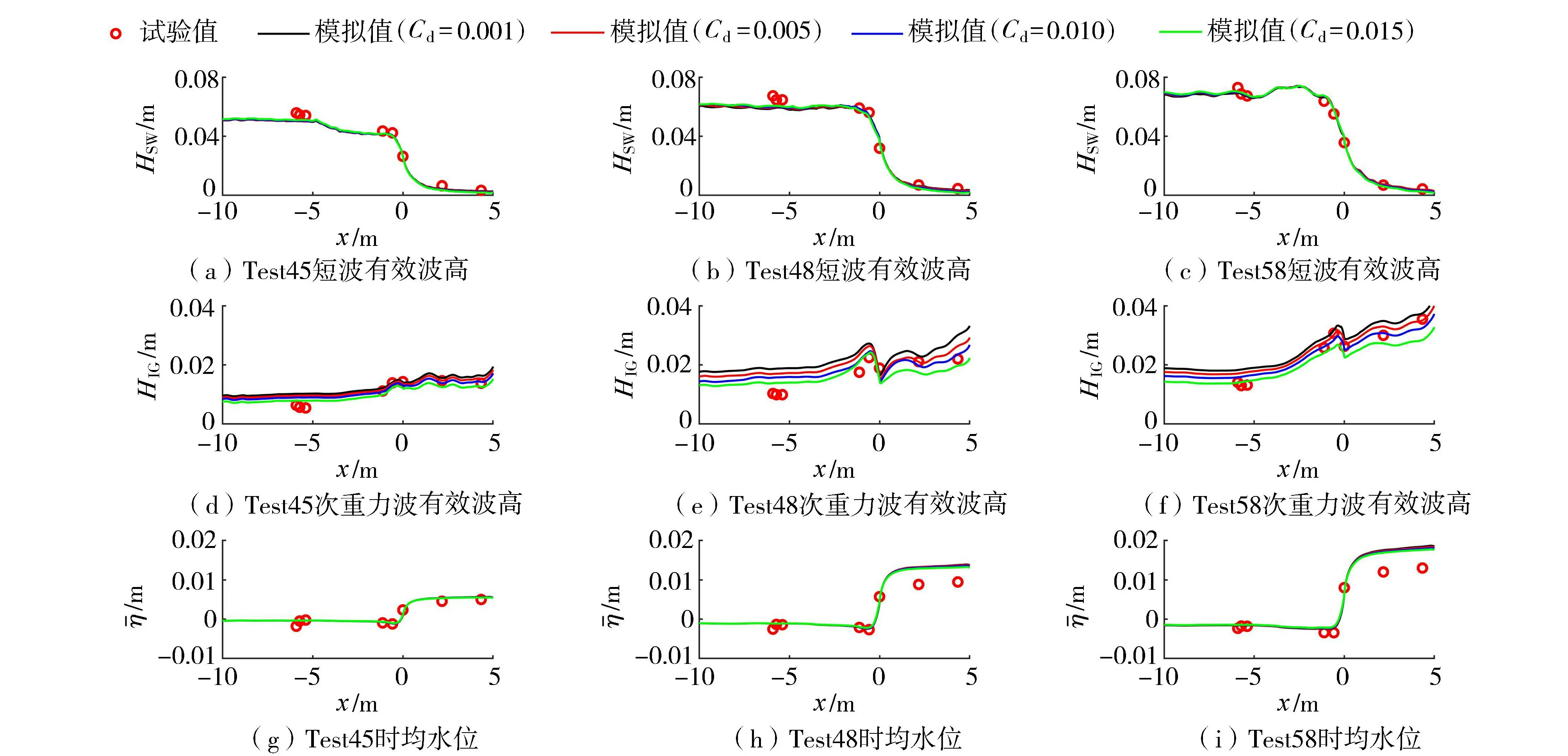
圖3 不同底摩阻系數條件下參數試驗值與模擬值空間分布對比Fig.3 Spatial distribution comparison of measured and predicted results with different friction coefficients

表2為破碎參數與底摩阻系數取不同值時由式(7)計算的短波、次重力波有效波高和時均水位的模擬精度，模型對于短波有效波高的模擬精度均可達到0.9以上，次重力波有效波高與時均水位模擬精度受入射波要素影響較大且后者對破碎參數與底摩阻系數變化基本不敏感。結合圖2、3分析認為Cbrk=0.55、Cd=0.010時，數值模擬結果更為理想，3組試驗次重力波有效波高模擬精度分別為0.83、0.74和0.91。

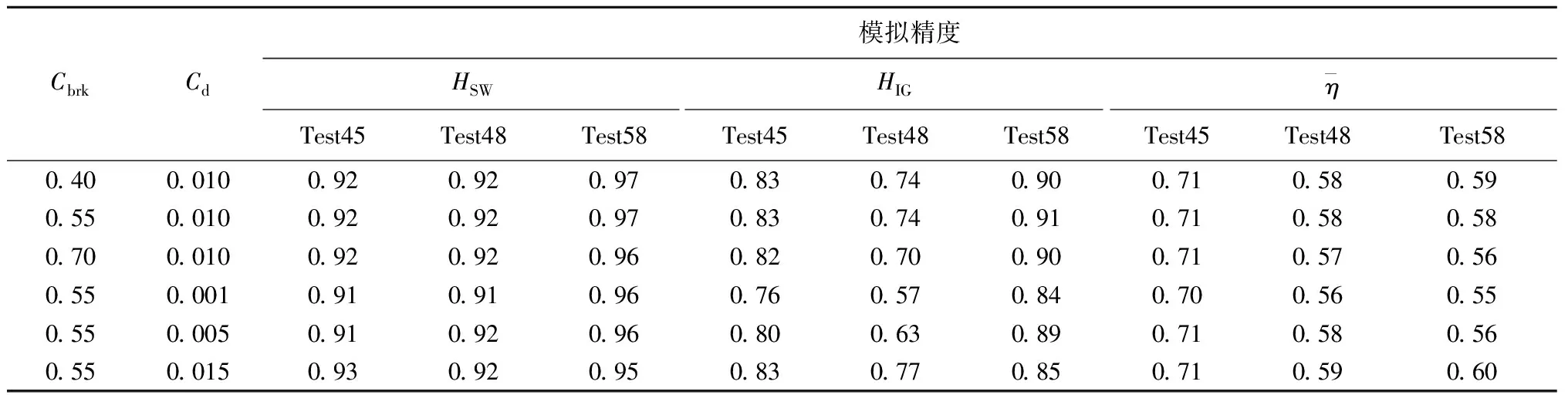
表2 不同參數下數值模型的模擬精度

3 次重力波的傳播過程與波能演變

采用前面驗證后的數值模型，仍基于Demirbilek等[17]的試驗(未專門指明時均以Test48為例)對次重力波的生成與傳播及相關的波能演變進行分析。

3.1 次重力波的生成與傳播

次重力波在近岸的兩種生成機制均與短波波群有密切的關系，可通過互相關分析的方法研究次重力波運動規律[4]。以兩組時域信號X(t)與Y(t)為例，歸一化后的互相關系數為

(8)

式中：τ——信號在時域上的延遲；σX、σY——X(t)、Y(t)的標準差；〈 〉——時間平均。相關系數RXY(τ)代表兩組時域信號在不同時間延遲上的相關程度，取值在-1～1之間，絕對值越大，兩組信號相關性越強。對短波包絡與次重力波波面時間序列進行互相關分析，并通過二者相關性在時域與空間域的分布可推知短波作用下次重力波的生成與傳播過程。次重力波波面時間序列可直接由低通濾波得到，短波包絡A(t)為

A(t)=|ηhf(t)+Hil{ηhf(t)}|lf

(9)

式中：Hil——希爾伯特變換算子；下標hf、lf分別表示高通濾波(f>0.5fp)與低通濾波(f<0.5fp)。

對Test48的模擬結果進行互相關分析。圖4(a)為測點G2處的短波包絡與沿程各點次重力有效波波面序列的互相關分析結果，黑色虛線對應測點G2位置，白色實線對應τ=0。測點G2在τ=0時存在一負相關峰，向岸靠近時該相關峰對應的時域延遲τ逐漸增大，對應入射的約束波，由于約束波波谷與波群包絡的波峰對應，因此與短波包絡呈負相關性，該相關峰幅值在礁前常水深處較小，在礁前斜坡上有顯著的增強。x≈0 m處，在τ≈5 s時出現的向岸正相關峰與離岸的負相關峰分別對應破碎點移動機制激發的向岸與離岸的次重力波，前者在τ≈12 s時傳遞至岸線處并在礁后斜坡反射，因此礁坪上次重力波有效波高呈駐波形態。入射的約束波相關峰在礁緣處消失，未能傳至礁坪上，可能在礁緣處反射或隨短波破碎而耗散。Su等[10]對于非平直礁坪地形的互相關分析顯示，高水位時約束波可傳遞至礁坪末端，而本工況中相對淹沒水深較小，因此礁坪上次重力波的生成由破碎點移動激發機制主導。在τ>20 s時礁緣離岸一側可以觀察到向岸傳播的正相關峰與反射的正相關峰的疊加，根據該相關峰對應的時域延遲，可能是破碎點激發的離岸次重力波在邊界發生了二次反射，模型中海綿層未能充分吸收離岸的長波。總體而言，數值模型較準確地模擬了兩種生成機制激發的次重力波在岸礁地形上的運動趨勢，與Pomeroy等[20]基于現場觀測的分析結果基本符合。

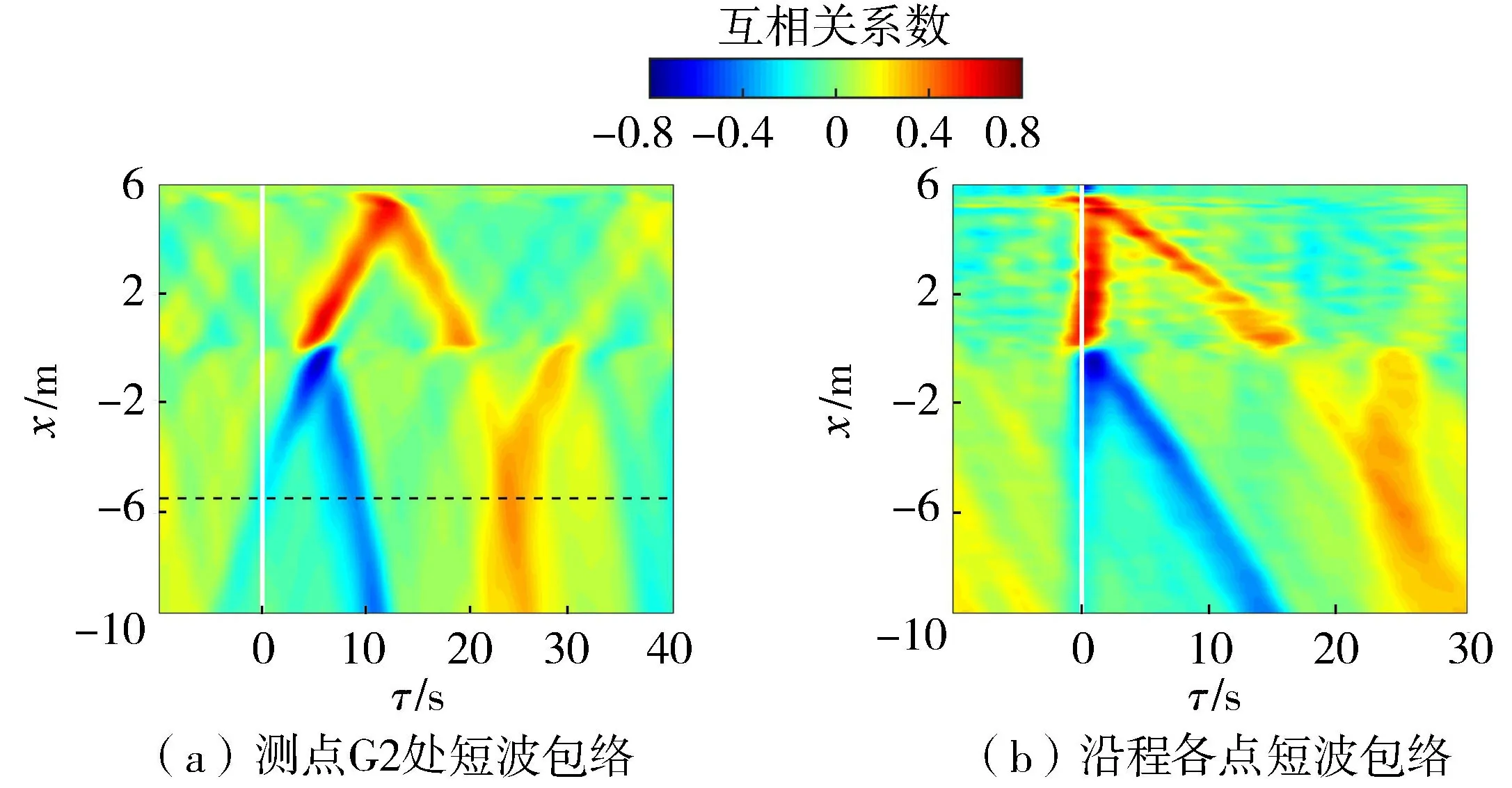
圖4 短波包絡與次重力波互相關分析結果Fig.4 Cross-correlation analysis results between short-wave envelopes and IG wave motions

圖4(b)為沿程各點短波包絡與相應位置的次重力波波面時間序列互相關分析結果，在礁前常水深處約束波負相關峰始終處于τ=0處，說明此時約束波與短波波群以相同速度傳播。隨著水深減小，該相關峰逐漸偏離白色實線出現在τ>0的一側，說明傳播過程中約束波的波谷逐漸滯后于短波包絡的波峰。

圖5對比了試驗值與模擬值在測點G2處短波包絡與其他部分測點次重力波信號的互相關性，模擬結果中兩種生成機制激發的次重力波對應的相關峰，在時域上出現的時間及各自演化趨勢與試驗結果基本吻合。此外測點G2試驗值在τ≈20 s時可觀察到一向岸傳播的負相關峰，該峰出現的時間約等于離岸的負相關峰以淺水波速傳遞至造波機處并反射回測點G2所需的時間，因此該相關峰為二次反射的長波，而數值模型在造波源后設置了海綿層，因此二次反射波的相關峰在時域上出現略滯后于試驗值，模擬結果顯示該相關峰反射過程中由負相關變為正相關，在Su等[10]的研究成果中也同樣發現該現象，因此模擬結果中測點G2在τ≈24 s時離岸的正相關峰與二次反射的正相關峰在此處疊加，相關性較試驗值更強，可能與礁前常水深處(測點G1～G3)次重力波有效波高的模擬值較試驗值偏大有關。

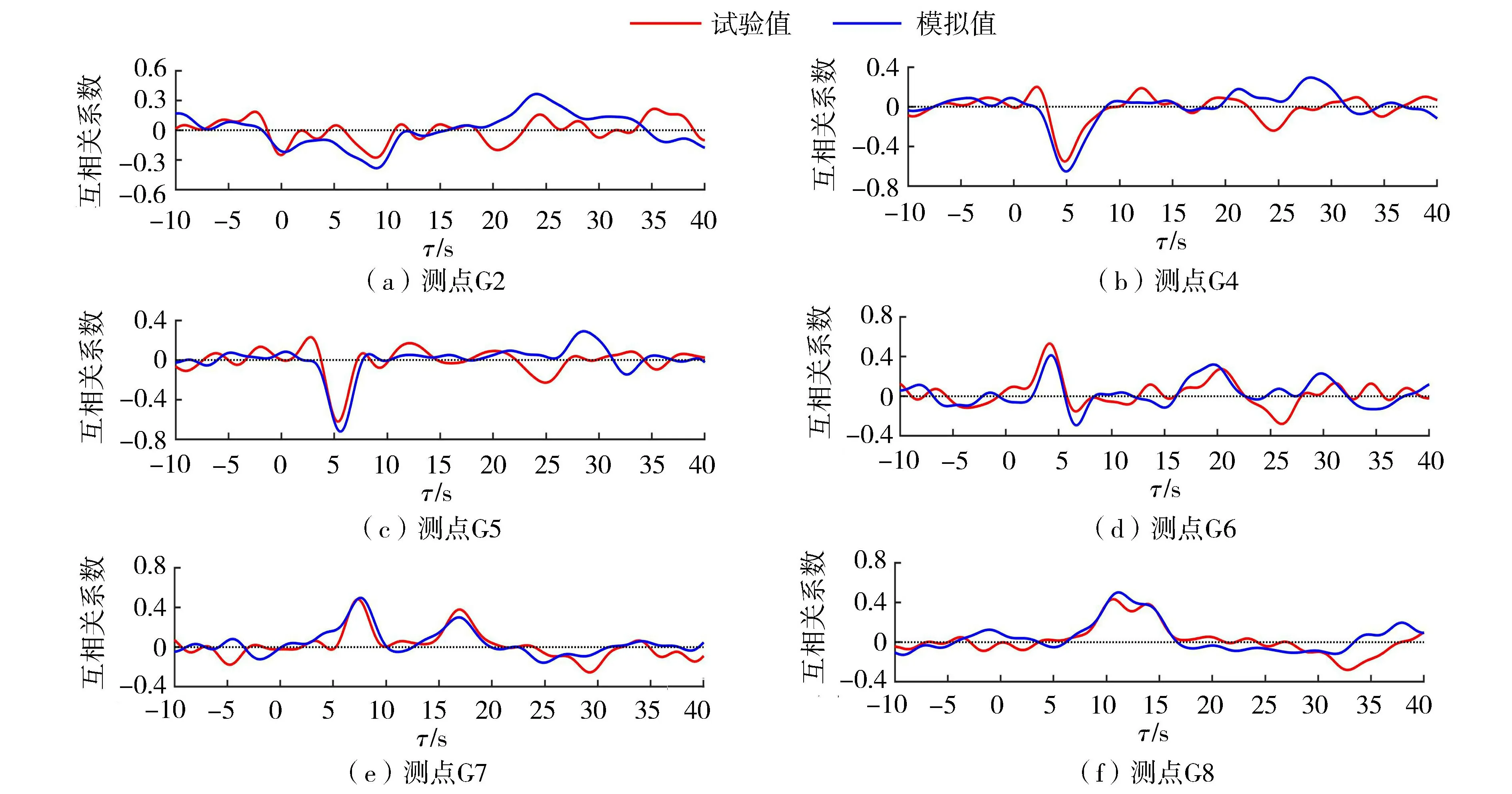
圖5 測點G2處短波包絡與各測點次重力波互相關分析Fig.5 Cross-correlation analysis between short-wave envelopes at G2 and IG wave motions at gauges

3.2 波能的沿程變化

波浪在岸礁地形傳播過程中伴隨著波能在低頻與高頻間的傳遞，該過程與次重力波關系密切。圖6(a)～(d)為波能譜的試驗值與模擬值對比，選取的4個測點分別代表了礁前常水深處、礁前斜坡、礁坪中部以及礁坪末端的頻譜結構，黑色虛線用于區分次重力波與短波頻段。測點G2模擬值與試驗值在譜峰頻段吻合較好，模型對低頻段頻率f≈0.03 Hz處的譜峰的高估導致此處次重力波有效波高模擬值較試驗值偏大；測點G5由于水深減小，譜峰頻率兩側的低頻與高頻波能均有所增長；波浪到達測點G7、G8時短波能量已大量耗散，模型較準確地捕捉了礁坪上幾個主要的低頻譜峰，測點G8在0.03 Hz附近的顯著譜峰與礁坪上理論一階共振放大頻率較吻合[9]。結合互相關分析結果和測點G2、G8在0.03 Hz附近顯著的譜峰來看，造成測點G2該頻率譜峰偏大的原因可能與模型礁后斜坡反射的次重力波以及邊界二次反射的次重力波形成的駐波有關，測點G2正好位于該頻率駐波波腹附近，而物理模型中由于長波的相位差異，測點G2在0.03 Hz附近波能并不顯著。圖6(e)～(h)為Test45與Test58在測點G2與G8的波能譜，試驗值與模擬值均吻合較好，但兩組工況同樣存在礁前0.03 Hz附近波能高估的現象。

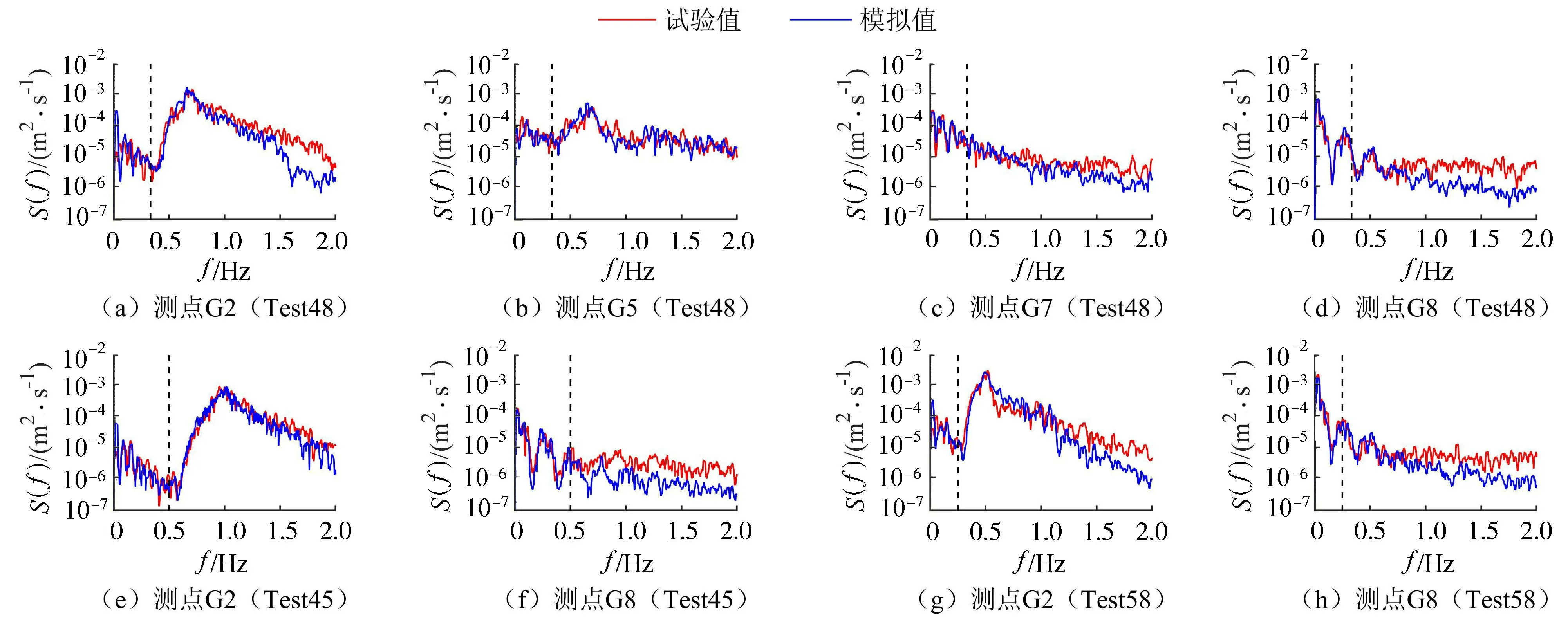
圖6 波能譜試驗值與模擬值對比Fig.6 Comparison of measured and predicted wave energy spectra

為了進一步研究波能在高頻與低頻間的傳遞過程，考慮到次重力波周期較長，采用Dong等[21]Morlet小波二階譜理論對波浪間的非線性相互作用進行分析，該方法相比基于傅里葉變換的二階譜法在相同條件下可達到更高的顯著性水平。對滿足f1+f2=f3頻率關系的波浪信號小波二階譜Bw表達式為

(10)

式中：WT(f,t)——波面時間序列小波變換結果；上標*表示復共軛。該二階譜表示時間T內頻率為f1和f2的波浪與頻率為f3的波浪間的相互作用程度，其中虛部代表能量的傳遞，虛部為正，能量由(f1，f2)傳遞至f3，如果為負則能量傳遞方向相反，虛部為0則波浪處于穩定狀態,該頻率之間無波能傳遞。圖7為Test48測點G2、G5、G8的試驗值與模擬值小波二階譜虛部圖。

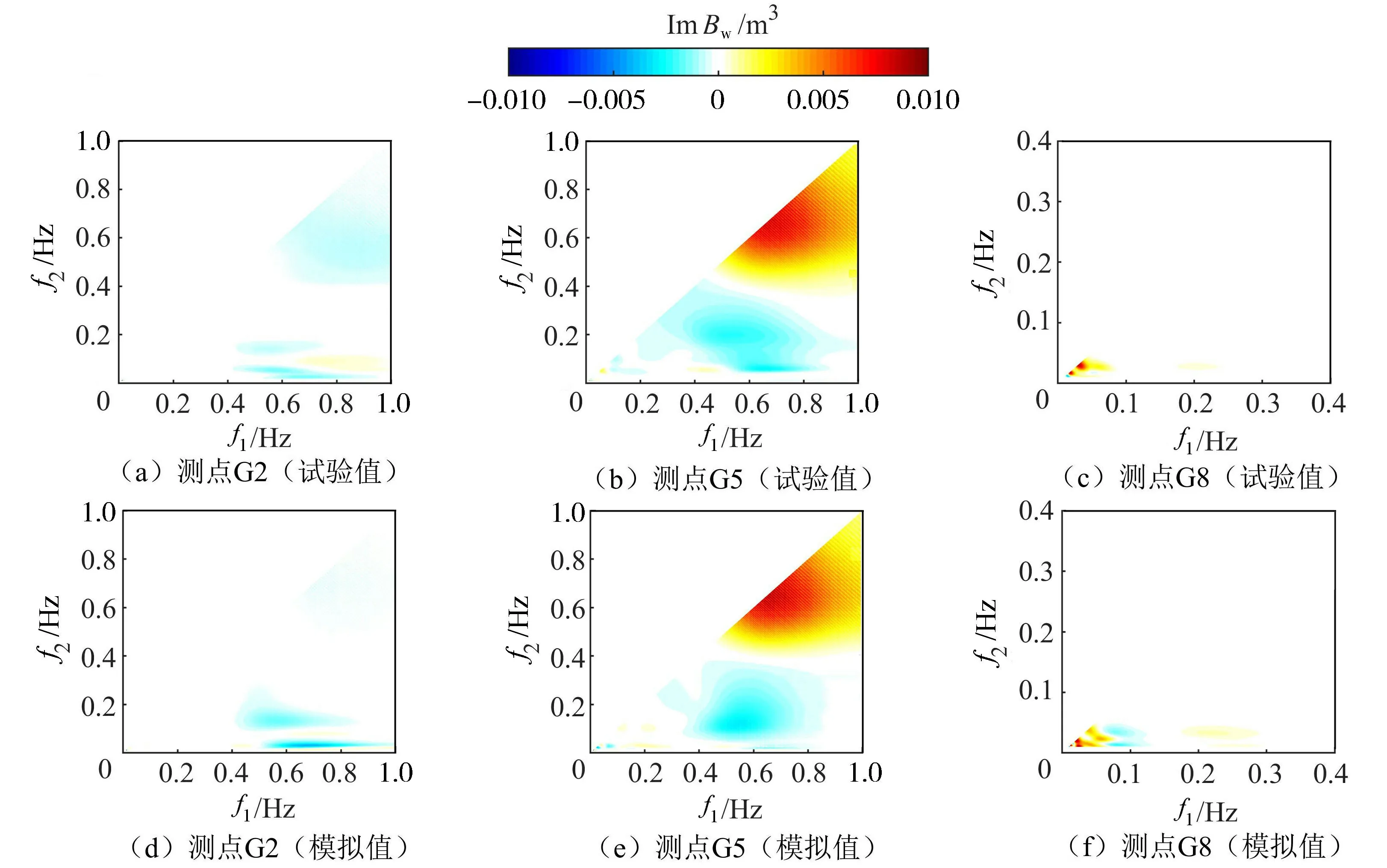
圖7 試驗值與模擬值的小波二階譜虛部Fig.7 Imaginary part of measured and predicted wavelet bispectra

測點G2(圖7(a)(d))波能傳遞主要發生在短波與頻率小于0.2 Hz的次重力波之間，能量由譜峰頻段向低頻段傳播，模擬值對于該處的非線性作用強度較試驗值偏大，但對于高頻段傳至譜峰頻段處的能量有所低估，同時試驗結果顯示(0.1 Hz, 0.7 Hz)～(0.1 Hz, 0.9 Hz)存在能量向高頻段的傳遞。試驗值與模擬值都觀察到0.03 Hz的長波從高頻段得到能量，結合前文分析結果，除短波與約束波外，該處的能量傳遞可能還來自短波與二次反射的向岸長波之間。

測點G5(圖7(b)(e))處存在較強的非線性相互作用，大量能量由譜峰頻段傳遞至高頻段，因此測點G5波能譜在2倍譜峰頻率處有較顯著譜峰，該過程中超諧波生成。同時0.05～0.35 Hz頻段附近的低頻波從高頻段獲得能量，造成約束波幅值增長。

測點G8(圖7(c)(f))顯示礁坪末端的非線性能量傳遞主要發生于次重力波之間，原因是短波受波浪破碎與礁坪底摩阻作用已大量耗散，到達礁坪末端的短波波能很小，雖然模型對于某些低頻處非線性能量傳遞的模擬值與試驗值略有差異，但總體趨勢基本一致。

4 結 論

a.FUNWAVE-TVD模型能夠較準確地模擬不規則波作用下岸礁地形上短波、次重力波有效波高及時均水位的沿程變化，敏感性分析結果顯示，在文中試驗地形條件下破碎參數Cbrk取0.55、底摩阻系數Cd取0.010時可獲得較為準確的模擬結果。

b.波浪在岸礁地形傳播過程中伴隨著波能的非線性傳遞，礁前次重力波頻段從譜峰頻段獲得能量；隨著水深減小非線性作用加劇，更多波能從譜峰頻段傳至高頻段與低頻段，該過程中向岸的約束波成長并滯后于短波波群；礁坪上的次重力波主要由破碎點移動產生，礁坪末端的非線性能量傳遞主要發生在次重力波之間。

c.數值模型較好地捕捉了次重力波在岸礁上的生成與傳播過程，但吸收邊界對于長波的吸收效果并不理想，可能導致礁前次重力波能量被高估。