基于VMD-ARIMA模型的BDI短期預測
張振朋



摘要:本文基于VMD算法和ARIMA模型,構建VMD-ARIMA模型,選取2015年10月28日到2018年4月30日的BDI日數據作為測試集,預測未來4天的BDI值。實證結果表明,VMD-ARIMA模型的預測結果優于ARIMA模型的預測結果。
關鍵詞:VMD算法;ARIMA模型;BDI;預測
1.引言
在波羅的海航交所發布的眾多指數中,波羅的海干散貨運價指數(Baltic Dry Index,BDI)是目前最具代表性的,BDI被稱為國際干散貨運輸市場走勢的晴雨表。為把握市場方向以及為航運企業提供參考,多年來對于BDI預測方面的研究已經相當深入。前期的研究是從單一時間尺度出發,預測BDI。李正宏[1]對剔除趨勢性和季節性因素的BFI,構建ARMA預測模型。杜昭璽[2],武佩劍[3]都建立ARMA模型對BDI進行短期預測。聶金龍和李序穎[4]使用ARFIMA模型對波羅的海干散貨運價指數進行預測。近年來,學者們開始從多時間尺度角度,預測BDI。劉子健[5],宋揚[6]和靳廉潔[7]先使用小波分析處理數據,再使用其他方法對運價指數進行預測,發現構建的組合模型預測精度優于單一模型。
本文構建VMD-ARIMA模型預測BDI。首先運用VMD[8]算法分解BDI序列,產生若干模態;然后用ARIMA模型分別預測各模態未來值;之后把各模態的預測值相加,即為BDI的預測值;最后比較VMD-ARIMA模型和ARIMA模型的預測效果。
2.模型介紹
2.1 VMD算法
VMD算法的總體思路是求解變分問題,具有十分堅實的理論基礎。該算法假設信號(序列BDI)是由K個具有中心頻率為ωk的模態分量(具有有限帶寬)uk(t)組成,由此構造變分問題。再通過乘法算子交替方向法不斷搜尋變分問題最優解,使得每個模態的估計帶寬之和最小。最終,自適應地將信號中的單一組分模態成功分離。
(1)變分問題
其中:{uk}={uu,u2,…,uk}表示分解出的K個模態分量uk(t),{ωk}={ω1,ω2,…,ωk}表示個分量的頻率中心,
(2)求解變分問題所用到的增廣拉格朗日表達式
(3)? ? 轉到頻域的表達式
(4) 轉換到頻域的表達式
(5)迭代停止條件
2.2 ARIMA模型
ARIMA模型是用于處理非平穩時間序列的一種模型,是時間序列預測分析方法的其中之一。ARIMA(p,d,q)中,AR是表示“自回歸”,p為自回歸階數;MA為“滑動平均”,q為滑動平均階數,d為把非平穩序列化為平穩序列所做的差分次數(階數)。
ARIMA(p,d,q)模型可以表示為:
其中是L滯后算子,d∈Z,d>0。
3.模型實證分析
3.1數據選取與分析
文中選取從2015年10月28日到2018年5月4日的BDI日數據(數據源自clarksons網站)。為了方便預測,文中把數據分為訓練集和測試集。訓練集的時間范圍為2015年10月28日到2018年4月30日(共624個數據),測試集的時間范圍為2018年5月1日到2018年5月4日(共4個數據)。
本文選用平均絕對誤差(MAE),均方根誤差(RMSE)和平均絕對百分比誤差(MAPE)作為衡量預測精度的指標,具體公式形式分別如下:
其中yt表示BDI的實際值,? 表示BDI的預測值,n是預測集數據的個數。
3.2 BDI的VMD分解
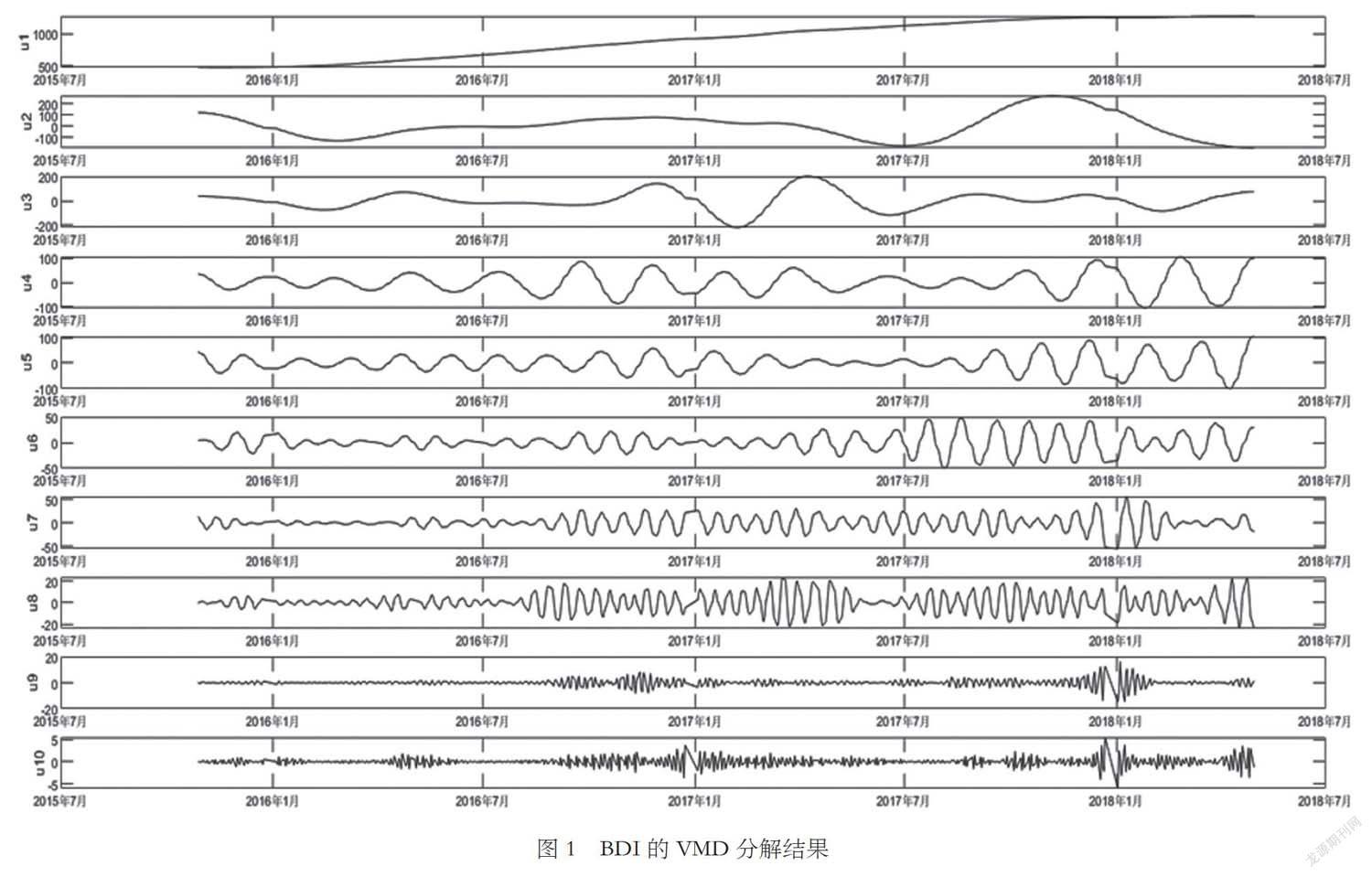
VMD算法的解產生的模態數量K需要提前設定,K對于VMD算法的分解效果有較大影響,本文是通過觀察中心頻率的方法選擇K值[9]。通過觀察不同K值條件下的中心頻率,本文中VMD算法的K=10,其他的參數設定為:懲罰因子? ?=2000,判別精度e=10-7。BDI分解的結果如圖1(從上到下依次為u1,u2,u3,u4,u5,u6,u7,u8,u9和u10。
3.3 模型預測結果
對VDM算法分解得到的各模態數據,使用ARIMA模型,預測10個模態和未來4天的值,10個模態對應日期的預測值相加,所得結果,即為VMD-ARIMA模型的預測值(見表1)。對訓練集數據,使用ARIMA模型預測BDI未來4天的值,所得結果即為ARIMA模型預測值(見表1)。測試集數據為未來4天BDI實際值(見表1)。
3.4 模型預測效果對比
本文使用模型評價指標MAE,RMSE和MAPE,評價VMD-ARIMA模型和ARIMA模型的預測精度,兩個模型的預測精度結果見表2。
從表2可以看出,VMD-ARMA模型的MAE,RMAE和MAPE均小于ARIMA模型的MAE,RMAE和MAPE,說明VMD-ARIMA模型的預測效果優于ARIMA模型的預測效果。
4.結論與展望
本文選取2015年10月28日到2018年4月30日的BDI日數據作為測試集,分別使用VMD-ARIMA模型和ARIMA模型,預測2018年5月1日到2018年5月4日BDI的值,結果表明VMD-ARIMA模型的預測精度優于ARIMA模型的預測精度。
本文所選取的時間區間比較單一,使用的預測模型僅為ARIMA模型,后續的研究可以從以下兩個方面繼續探索。
一方面,可以選取多組時間區間,驗證VMD-ARIMA模型預測精度優于ARIMA模型預測精度這一結論的適用性。另一方面,可以選用新的預測模型,如神經網絡(BP)和SVM算法等預測模型,比較組合預測模型和單一預測模型的精度。
參考文獻:
[1]李正宏,袁紹宏.波羅的海運價指數相關性分析[J].水運管理,2004(08):24-27.
[2]杜昭璽,李陽,靳志宏.波羅的海干散貨運價指數預測及實證分析[J].大連海事大學學報(社會科學版),2009,8(01):77-80.
[3]武佩劍,陳永平.波羅的海干散貨運價指數波動規律及對我國的啟示——國際干散貨運輸市場走勢的晴雨表[J].價格理論與實踐,2010(11):50-51.
[4]聶金龍,李序穎.波羅的海干散貨運價指數的ARFIMA模型研究[J].中國水運(下半月),2009,9(04):57-58.
[5]劉子建.基于小波理論的國際干散貨航運市場周期波動及預測研究[D].大連海事大學,2009.
[6]宋揚.金融危機下的國際干散貨運價指數預測研究[D].大連海事大學,2009.
[7]靳廉潔.基于支持向量機的干散貨運價指數預測研究[D].大連海事大學,2010.
[8]DRAGOMIRETSKIY K,ZOSSO D.Variational Mode Decomposition[J].IEEE Transactions on Signal Processing,2014,62(3):531-544.
[9]劉長良,武英杰,甄成剛.基于變分模態分解和模糊C均值聚類的滾動軸承故障診斷[J].中國電機工程學報,2015,35(13):3358-3365.

