不中斷交通高速公路改擴建交通仿真參數標定

陳雅楠， 修 輝， 李美玲， 冉 晉， 馬曉剛

(1.山東建筑大學 山東高校重點實驗室道路與交通工程實驗室， 濟南 250101； 2.山東省交通科學研究院， 濟南 250102； 3.山東高速股份有限公司， 濟南 250101)

隨著區域經濟的快速發展和汽車保有量的迅速增長，先期建成的高速公路有很多已近飽和狀態，通行效率下降嚴重，亟需改造提升。高速公路改擴建是一種很重要的改造方式，此類公路多為超大中修期服役，受數據采集設備和調查工具局限，較難得到改擴建道路持續真實的運行狀態，借助仿真手段搭建微觀交通模型[1]。近些年，PTV研發的VISSIM軟件在道路交通研究領域廣泛應用，但其中大量的獨立參數顯現的是德國交通系統特征，并不符合我國道路的實際情況，因此模型缺省值參數的標定工作對于特定工程的研究是必要的。

交通仿真參數標定主要有宏觀參數校正法和全微觀參數校正法，前者改變模型參數的輸入值，以縮小宏觀數值與實測值誤差；后者利用加速度、車頭時距、停車間距等實測微觀數據校正[2]。涉及到的標定參數集各自取值范圍龐大且無交集，國內外學者通過提高尋優效率的算法進行全局枚舉工作。如孫劍等[3]以城市信號燈控交叉口為例，建立遺傳模擬退火啟發式算法，實現仿真參數的自動化校正；章玉等[4]發現模型標定時SPSA算法比GA算法快1.7倍；韓國華等[5]基于PSO算法提出完整校正流程；楊艷芳等[6]驗證了SOGA算法應用；還有一些學者著力于改進遺傳算法，進一步提高精確性和計算速度[7]。以上大多是針對復雜城市道路網系統進行的研究，由于不同場景交通流特性的差異，對于高速公路改擴建工程的參數標定還需進一步探討。

參數標定的實質是不斷調整微觀交通仿真模型缺省值，選取模型輸出結果與實測值誤差最小的校核指標和參數，使標定后的仿真模型與道路實際運行狀況更為接近。本文基于不中斷交通高速公路 “雙側加寬”形式的仿真模型，研究指標參數取值與標定方法改進。標定好的模型能更好地呈現改擴建期間交通運行狀況，可應用于濟青高速后續相關問題的仿真研究，為今后類似的改擴建工程項目仿真參數標定提供參考依據。

1 交通仿真參數標定流程

改擴建期間因“邊通車、邊施工”，難以獲得大量準確的微觀實測數據，故應用現有的參數校正體系[8]，參考周晨靜等[9]有關全局參數敏感性分析的研究，依據微觀交通仿真試驗自身特性和方差分析理論，降低標定工作的復雜度。具體標定流程如下：

1) 提出高速公路改擴建工程模型駕駛參數選取依據，采集相關數據；

2) 對待標定指標和參數組合進行敏感性分析，檢驗各參數變化對模型運行結果的影響程度，篩選出對交通運行狀況具有較大影響的重要指標和參數集，以簡化標定工作量；

3) 設計交通仿真方案。利用科學有效的正交表格安排分析多因素、多水平的交通仿真試驗，模擬驗證具有代表性的參數水平組合，分析并評價仿真運行結果以全面了解目標問題，找出具備均勻分散、齊整可比的最優水平組合，作為不中斷交通的高速公路改擴建工程模型參數標定方案[9-10]，如圖1所示。

圖1 模型參數標定流程

2 敏感性分析和參數標定的方法

2.1 參數選取和數據采集

2.1.1 標定參數選取

仿真模型中，國內外的車輛尺寸、道路寬度及類型等物化設施無明顯差異，但駕駛習慣不同，需考慮駕駛行為的參數模型，如期望車速、跟馳模型和車道變換模型等。改擴建期間高速公路在道路線形和施工環境等方面存在較大的不同，極易引起駕駛員的心理波動。面向高速公路的跟車行為以Widemann-99模型為選取依據，變道行為使用Willmann和Sparamann的基于行為閥值的換車道模型，核心模型采用德國大學教授的生理-心理模型[11]。

因此，考慮不中斷交通的改擴建高速公路特性，選取2類關鍵參數進行標定：一是影響交通流穩定性較大的因素j作為校核指標Ai，包括目標道路的總流量、車輛行程時間、平均延誤、平均排隊長度、平均速度；二是選擇基于道路特征的微觀參數j作為待標定參數Nj，包括跟車模型參數CCm(停車間距、車頭時距、跟車變量、前后車的縱向擺動約束、進入跟車狀態的閾值、消極跟車狀態的閾值、積極跟車狀態的閾值、車速振動、振動加速度、停車的加速度、80 km/h車速時的加速度)和換道模型參數Cn(最大減速度、可接受的減速度、消散前的等待時間、最小車頭空距)。

2.1.2 實際數據采集

實際數據采集是特征路段模型建立的準備工作，在一定程度上影響交通流模擬的真實性，是參數標定中極其重要的基礎性工作。通常采用隨機抽樣法保證樣本的無偏性，樣本的多少取決于研究精度需求[12]。

2.1.3 待標定參數驗證

通過敏感性分析獲得待標定指標和參數集，可直接采取正交試驗設計法標定。將仿真輸出值與實測值相對誤差作為評價指標，誤差值越小效果越好。考慮到交通調查的誤差以及道路交通運行狀態本身所具有的隨機性，當擬定參數誤差指標控制在5%之內時，即認為仿真值和實際調查數據有較好的擬合度，通過了有效性評價，可滿足模型標定的精度要求，如式(1)：

(1)

式中：Q為調查實測值；Q′為仿真運算值。

2.2 參數指標組合敏感性分析

此工作需借助搭建的交通微觀仿真模型，可參考文獻，選擇便捷、精確的敏感性分析方法[13],對具有代表性的多個標定指標和駕駛微觀參數重新組合，并確定標定指標及指標參數集。

2.2.1 參數指標組合

將眾多參數組合成不同水平的指標參數集Ai·Nj，通過構建參數指標組合矩陣Pij進行敏感性分析，選出每個指標對應的標定參數相關性最大組合，如式(2)：

CC1…CCnC1…Cm

P=[maxPij]

(2)

式中：Pij為參數指標組合矩陣；P為參數指標最優組合；Ai= [A1，A2，…，Ai]，i= 1，2，3，4，5為校核指標集合；Nj=[CCn，Cm]，j= 1，2，…，n+m為標定參數集合；CCn= [CC0，CC1，…，CCn]，n= 0，1，2，…，9為跟馳模型參數集合；Cm= [C1，C2，…，Cm]，m= 1，2，3，4為變道模型參集合；λi,n+m為判斷指標。

2.2.2 參數敏感性分析

敏感性分析又稱為參數靈敏度分析，是對仿真模型輸入變量對輸出變量影響程度的定量描述方法。適用于校正參數集篩選，預先有效排除標定指標重要度較低的駕駛行為參數，以減少標定工作量。構建仿真試驗分析矩陣如式(3)～式(7)，判定仿真參數對校核指標的敏感性。

(3)

(4)

(5)

(6)

(7)

式中：Xij為仿真試驗分析矩陣；隨機種子所取水平數l= 1，2，3，…，n；k= 1，2，3，…，m為仿真參數變化水平；Iij為參數變化引起試驗結果標準差的算術平均值；I′ij為隨機因子變化引起試驗結果標準差的算術平均值；STDEVA為樣本標準差函數；λi,n+m為判斷指標，如果λi,n+m>1.5，判定仿真模型參數對校核指標具有影響，如1<λi,n+m<1.5，有影響，不顯著，否則λi,n+m<1，無影響。

2.3 參數標定方法

全面試驗法的優點在于對各因素與試驗指標的關系剖析清楚，缺點是不做重復試驗無法區分主次因素；簡單比較法次數少但考察的因素水平僅限于局部區域。由于改擴建工程模型涉及的實際數據難以采集，亦沒有數學公式科學表示，標定極為復雜，因此根據研究目的，選擇相關指標與參數組合進行敏感性測試與分析。經過綜合考慮決定，選擇使用不同水平數之間有交互作用的多指標正交試驗法，既可減少試驗次數，提高效率，又可利用科學的規格化表格安排多因素試驗，次數可控、精準高效，適合改擴建模型參數標定[14-15]。

3 案例應用

3.1 工程介紹與特征路段選取

選取濟青高速公路改擴建工程中青島方向K306+500路段作為參數標定工作的研究對象。既有濟南—青島高速公路為雙向4車道，改擴建后采用雙向8車道高速公路標準，是我國目前一次性改擴建里程最長、投資最大的高速公路改擴建工程，也是國內首次采用下面層行車的改擴建保通方案。

K306+500路段為雙向2車道，經過中分帶開口后變換為單車道的直行路段，中分帶開口長225 m、寬3 m，車道寬度為3.75 m，如圖2所示。實際數據采集時間為2018年4月，交通量為1 450 pcu/h，選取單向輸入方式，入口交通流量輸入2 000 pcu/h，車輛運行期望速度為80 km/h，中分帶開口段限速40 km/h，小汽車與貨車、大型客車的流量比為7∶2.5∶0.5，仿真時長3 600 s，有效周期時長選取其中第600 s ～ 3 000 s。

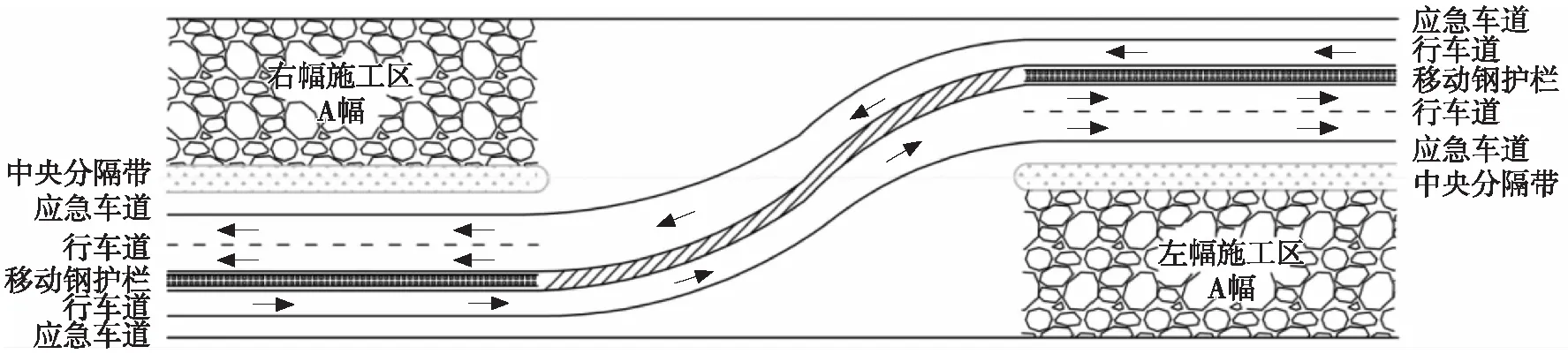
圖2 K306+500段車流轉換形式

3.2 試驗方案設計

3.2.1 指標參數選取

仿真模型輸出參數：600 s ～ 3000 s內整個路段的總流量、行程時間，中分帶開口段車輛的平均延誤、平均速度、中分帶開口段上游車輛的平均排隊長度，共5個標定指標。待標定的14個微觀參數(跟馳參數CCm和換道參數Cn)默認值及取值范圍參考使用手冊[11]。

3.2.2 敏感性分析

采用插值法將各個參數在其取值范圍內10等分，使每個仿真參數具有11個取值水平，仿真隨機種子選取20、60、100、140、180共5個水平，在不同水平的隨機種子下每次仿真只變化1個參數的水平值，其他參數取值設為默認值。

現以停車間距(CC0)為例對此路段總流量的敏感性進行分析。獲取在仿真參數CC0數值變化和隨機種子變化條件下的試驗結果，按照式(3)～式(7)分別計算仿真輸出的試驗結果標準差，其最終判別指標為1.33，判定停車間距對整個路段總流量有影響但并不顯著，具體結果如表1所示。

按照以上分析方法可得出其他微觀標定參數對校核指標的敏感性狀況，如圖3所示。其中CC1、CC2、CC8三個參數對5個校核指標都有顯著影響，CC7對流量和平均速度有顯著影響，CC3對延誤、行程時間和排隊長度有顯著影響。考慮到數據采集的便捷性，選取整個路段的車流量作為標定指標，CC1、CC2、CC7、CC8四個參數為標定參數。

3.2.3 正交試驗法參數標定

敏感性分析的標定指標結果為路段車流量，待標定參數為車頭時距(CC1)、跟車變量(CC2)、振動加速度(CC7)、停車的加速度(CC8)4個微觀參數，每個參數劃分3個水平。選用3水平4因素正交表L9(34)進行仿真試驗，按照正交表中各參數標定試驗方案的水平組合運行VISSIM仿真，9個方案分別在不同的隨機種子下運行5次，對試驗結果進行極差分析，得出不同因素不同水平值對試驗指標的影響程度及主次順序，進而確定最優因素水平組合：CC1=1，CC2=5，CC7=0.6，CC8=7。

3.3 標定參數精度分析

敏感性分析選取5個標定指標和14個微觀參數，選取受參數影響較多的指標作為微觀交通仿真的參數標定指標。正交試驗將路段車流量指標與待標定的4個微觀參數重新科學組合成參數集最優解，再次仿真輸出的流量為1 428，標定后的最優仿流量值與實測數據接近，誤差在可接受范圍內。

對4個微觀參數標定結果的均值進行主效應驗證，每個參數劃分為3個水平，如圖4所示。由圖4可知，趨勢線不平行于橫軸表示存在主效應，線越陡峭主效應量值越大，故經驗證所用標定組合有效。

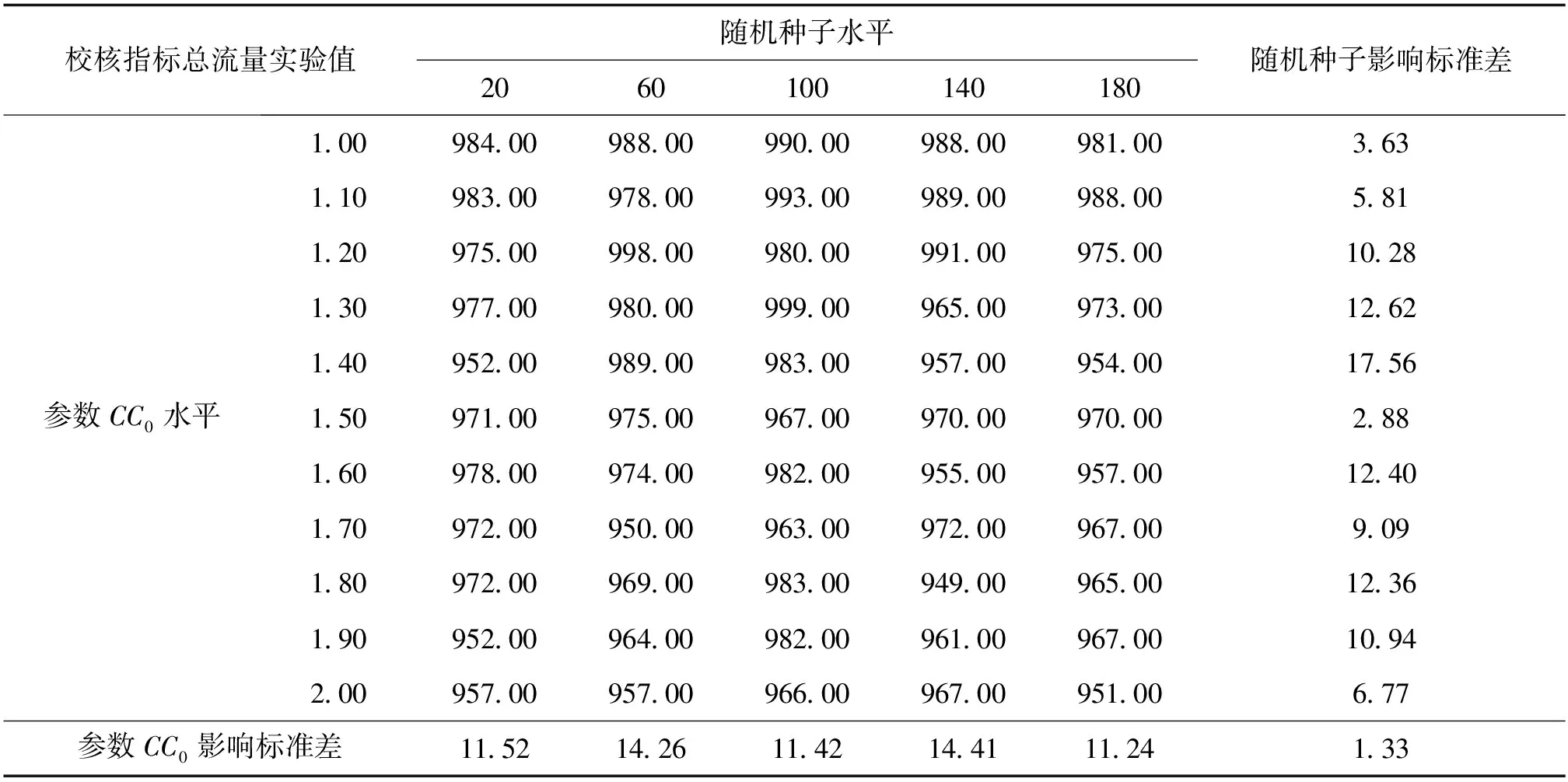
表1 停車間距(CC0)對總流量敏感性分析

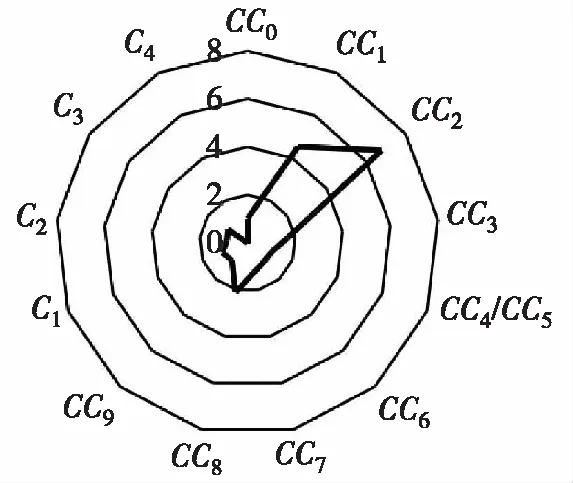
(a) 延誤對參數敏感性

(b) 流量對參數敏感性

(c) 速度對參數敏感性

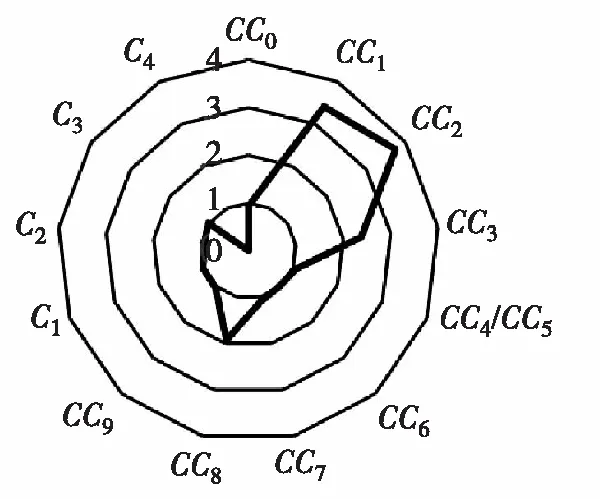
(d) 排隊長度對參數敏感性

(e) 行程時間對參數敏感性

最終微觀參數標定結果如表2、表3所示，其他參數保持缺省值不變。

圖4 標定結果均值的主效應驗證

表2 期望車速標定參數結果

表3 駕駛行為標定參數結果

4 參數標定結果對比分析

為了驗證本文提出的敏感性分析與正交試驗相結合的參數校正方法具有科學性、實用性和有效性，搜集國內外部分高速公路的參數標定結果進行對比分析，結果如表4所示。

A列采集美國880號州際公路自南向北方向(簡稱1-880N)交織區內1 d的實際數據，目的是建立實時事故風險預測模型[16]。將每30 s車輛速度仿真結果值與速度分布默認值、計算事故風險值與事故風險分布默認值比較，發現此模型CC4～CC7校正值與缺省值差別較大。B列以廣深高速公路廣州收費站建模[17]，標定值變化幅度較大，表明該模型可作為大流量高速公路普通路段的參考依據。C列以新建邢衡高速為仿真對象[18]，考慮了匝道入口處的交通流特性，針對部分跟馳參數進行校正。

表4 不同高速公路的參數標定結果對比

D列是本文案例標定的參數值。通過對比分析可知，不同的場景參數有明顯差異，需要特殊問題特殊研究。本文提出的方法以實際地點車輛速度的調查數據對期望車速進行詳細標定，并選擇14個跟馳模型和變道模型的參數進行標定，全面具體，貼近實際，標定好的模型可同時對不間斷交通的高速公路改擴建期間大量問題路段的仿真進行研究。此外，經由完善的標定方法借助科學有效的方式篩選出影響程度較高的參數水平組合，在一定程度上可以減少數據采集和標定工作量。

5 結束語

針對不中斷交通的改擴建工程特點，完善了仿真參數標定流程，提出了敏感性分析與正交試驗相結合的參數校正方法，并校正關鍵參數指標涉及的駕駛行為參數模型。

以濟青高速改擴建工程為例，通過敏感性分析篩選出5個基于道路特征的微觀參數j作為校核指標Ai，基于參數j選取14個跟馳模型參數CCm和換道模型參數Cn，作為待標定參數Nj，由此克服了指標選取的盲從性，降低了標定復雜度和工作量。通過正交表格設計科學有效的仿真方案，找出具備均勻分散、齊整可比的最優水平組合作為參數標定結果。經案例應用分析并評價仿真運行結果發現，CC1=1、CC2=5、CC7=0.6、CC8=7為最優因素水平組合。研究結果為今后類似的改擴建高速公路仿真模型構建提供了借鑒。