公路邊坡數值模型幾何尺寸的影響分析

潘永堅， 王華俊， 卿翠貴， 張 建

(1.浙江省工程勘察設計院集團有限公司， 浙江 寧波 315012； 2.寧波大學 土木與環境工程學院， 浙江 寧波 315211)

在公路邊坡設計過程中通常涉及到大量的數值計算，以確定最優坡比及相應的支護方案，數值計算結果是工程決策的重要依據[1-2]。為了提高計算效率，數值計算過程要在計算效率與計算準確性之間達到平衡。由于數值模型存在邊界約束條件，構建合理的數模是獲得可靠參考數據的前提[3]。閆東晗等[4]對一邊坡模型(取右側邊界R= 2.5H、下側邊界B= 2H、左側邊界L= 1.5H，H為坡高，各參數的意義見圖1)利用強度折減法計算時，發現采用二維模型左側邊界對計算結果影響次于下邊界。郭昊天等[5]在對路塹高邊坡進行分析時，采用了類似R=H、B=H、L=H的等邊界尺寸模型進行計算，并對相關工程案例進行了分析。任晉嵐等[6]在進行強度折減計算時，為了減小尺寸效應的影響，建模時將模型的邊界尺寸盡可能擴大，以減小邊界約束條件對計算結果的影響。孫志杰等[7]在物理模型試驗中，采用坡體寬度大于高度的物理模型試驗，以降低模型尺寸邊界對物理試驗結果的影響。Ma等[8]在三維數值分析中比較了運算時間長度，當W=H時(W為三維模型寬度)，所得三維模型進行分析結論較為可靠。張坤勇等[9]采用W> 6H的模型進行計算時，發現可以將三維問題簡化為二維問題來處理，以減小運算時間，但當W< 3H時，數模的三維效應應當被考慮。陳達章等[10]認為W取值較小時，會對計算結果有較大影響，取坡體模型寬度為坡高的一倍以上時可滿足精度要求。

圖1 邊坡數值模型幾何參數示意

在工程應用過程中，盛曉杰等[11]通過延長模型邊界的方法進行計算，但是并沒有考慮到模型尺寸與計算結果可靠性的關聯。謝洪斌等[12]在研究高邊坡在動力作用下的動力響應特征時所采用的模型邊界取值偏小，其對結果的影響也缺乏進一步說明。王鈺[13]在對經典模型進行計算時，分析了3種典型模型，但所采用的尺寸各不相同，模型尺寸對分析結果的影響并未詳細說明。

基于以上文獻分析，目前對坡體數模尺寸的選用并沒有統一的分析結論。在構建數值模型過程中，通常不考慮計算效率，取較大的邊界值以獲得準確的計算結果。為了獲得較準確的分析結果及較高的計算效率，數值模型尺寸到底該如何設計，是值得進一步討論的問題。鑒于此，本文采用系統分析的方法，分別討論基于強度折減法[14]及有限差分軟件(FLAC3D)[15]在進行二維及三維邊坡模型分析時，數模尺寸對分析結果的影響，闡述數值模型對幾何尺寸的敏感性，并給出針對模型構建的實用性建議。

1 二維模型邊界尺寸影響分析

初始分析模型先在有限元軟件ANSYS中構建，劃分網格后將模型的節點及單元尺寸信息導入FLAC3D中構建最終的分析模型。所有模型均采用相同的網格密度，劃分的最小網格單元體尺寸為2 m。數模的上部為自由界面，無任何約束，下邊界為全約束，左右界面采用法向約束，即不可水平方向發生位移。取坡高H= 20 m，左側邊界L= (0.25-3.5)H，右側邊界R= (0.25-3.5)H，底部邊界B= (0.25-3.5)H。土體的強度計算本構關系采用經典的摩爾-庫倫準則。計算過程中涉及到的土的物理參數為：土體重度γ= 20 kN/m3，內聚力c= 20 kPa，內摩擦角φ= 20°，彈性模量E= 30 MPa，泊松比v= 0.3。

1.1 模型幾何尺寸與坡體安全系數的關聯分析

1) 3處邊界取值相同的情況

設計如下試驗：取L=R=B=C，C有0.25H、0.5H、H、1.5H、2H、2.5H、3H、3.5H等共計8組取值，坡角θ=45°。通過等比例逐步擴大模型的邊界尺寸，計算得到的安全系數FS見表1。

表1 等邊界條件下的安全系數求解結果

從表1可以看出，計算所得的坡體安全系數隨邊界取值的不同呈波動變化。在該組試驗中，最大安全系數與最小安全系數的幅度相差7.2%，從第3組取值開始，模型尺寸越大，計算所得安全系數逐漸遞增，計算所需要的存儲空間及計算時長也逐步增加。

根據以上分析，當模型的邊界約束尺寸較坡體本身的尺寸較大時，計算所得的安全系數相對較大。但這個較大的安全系數并不是對工程實際的真實反映，因為求解模型來源于簡化的工程實體，以犧牲運算效率為代價，為增加數值分析結果與實際問題解的接近程度的做法，并沒有具體的實際意義。因此，在合理的取值范圍內，解算結果偏于安全的邊界取值才是數值分析搜尋的目標。針對表1的計算結果，數值模型中3處邊界取值均為1.5H時，所得的安全系數相對較小，用此時的安全系數評價邊坡的穩定性結果偏于安全，可用于實際參考。

為了進一步分析坡角大小對計算結果的影響，分別取坡角為30°、39°、45°、51°、60°進行試驗，邊界取值從0.5H遞增至2.5H，等間隔設置遞增幅度，結果見圖2。由圖2可知，坡角會對計算結果產生影響，隨著模型邊界尺寸的增加，坡角分別為為30°、39°、45°、51°、60°時，安全系數的波動幅度分別為1.5%、2.8%、4.1%、2.2%、1.6%。其中，坡角取值θ=45°時，安全系數的波動幅度最大，可作為分析邊界尺寸時的一個典型的坡角取值情況。

圖2 坡角及邊界大小對分析結果的影響

2) 3處邊界取值不相同的情況

以上分析是建立在坡體左側邊界、右側邊界、上邊界取值相同的假設情況下進行的。為深入分析3處邊界取值不等的情況下坡體數模尺寸對分析結果的影響，試驗根據前述分析，取典型情況(坡角θ=45°)進行分析。具體方案為：將數模的右側邊界和下邊界固定取值為1.5H，左側邊界則由0.5H遞增到3.5H，找到最佳的左側邊界取值；再在此基礎之上，固定左側邊界和下邊界，變化右側邊界，找到最佳的右側邊界取值；最后變化下邊界，確定最優的模型邊界取值。試驗設計方案以結果繼承的方式進行，主要目的是為了有效控制試驗次數，使問題簡化可解。

得到的分析結果見表2。分析可得，左側邊界的變化對分析結果有一定影響，隨著左側邊界尺寸的增加，計算所得結果略有波動，最大變化率為1.4%。其中，考慮到第1組試驗因左側邊界取值太小，認為邊界約束條件對計算結果產生較大影響。左側邊界取值H和1.5H時所得的安全系數較小，左側邊界取值為H時，所得安全最小為1.148。當左側邊界取值不小于2H時，計算所得坡體安全系數近似趨于穩定。考慮到使安全系數計算收斂的邊界值因坡角等取值的變化而變化，根據前文對數值分析結果取用原則的界定，確定左側邊界的最優取值為H，即可保證計算結果的可靠性及運算效率。

表2 左側邊界對分析結果的影響

根據表2的分析，設計下一步試驗：將模型的右側邊界尺寸由0.5H逐步遞增到3.5H(增幅固定)，左側邊界與下邊界分別固定為H和1.5H，所得計算結果見表3。根據表3的結果，認為第1組取值不可靠，不予考慮。在左側邊界取值H、下邊界取值1.5H的情況下，右側邊界取值為H及1.5H時所得的安全系數最小，均為1.148。

為進一步確定下邊界的最佳取值，取左側邊界為H，右側邊界分別取值H(A組試驗)與1.5H(B組試驗)，下邊界取值由0.5H遞增至3.5H，遞增幅度為0.5H，所得安全系數見表4。由表4可知，在右側邊界分別取值H與1.5H時，隨著下邊界的變化，安全系數均有一定波動，右側邊界取值H、1.5H時，波動幅度分別為2.8%、4.1%。當左側邊界取值為H、下邊界取值為1.5H，右側邊界取值H和1.5H時，所得安全系數均為1.148。由此可知下邊界的最優取值為1.5H。

表3 右側邊界大小對計算結果的影響

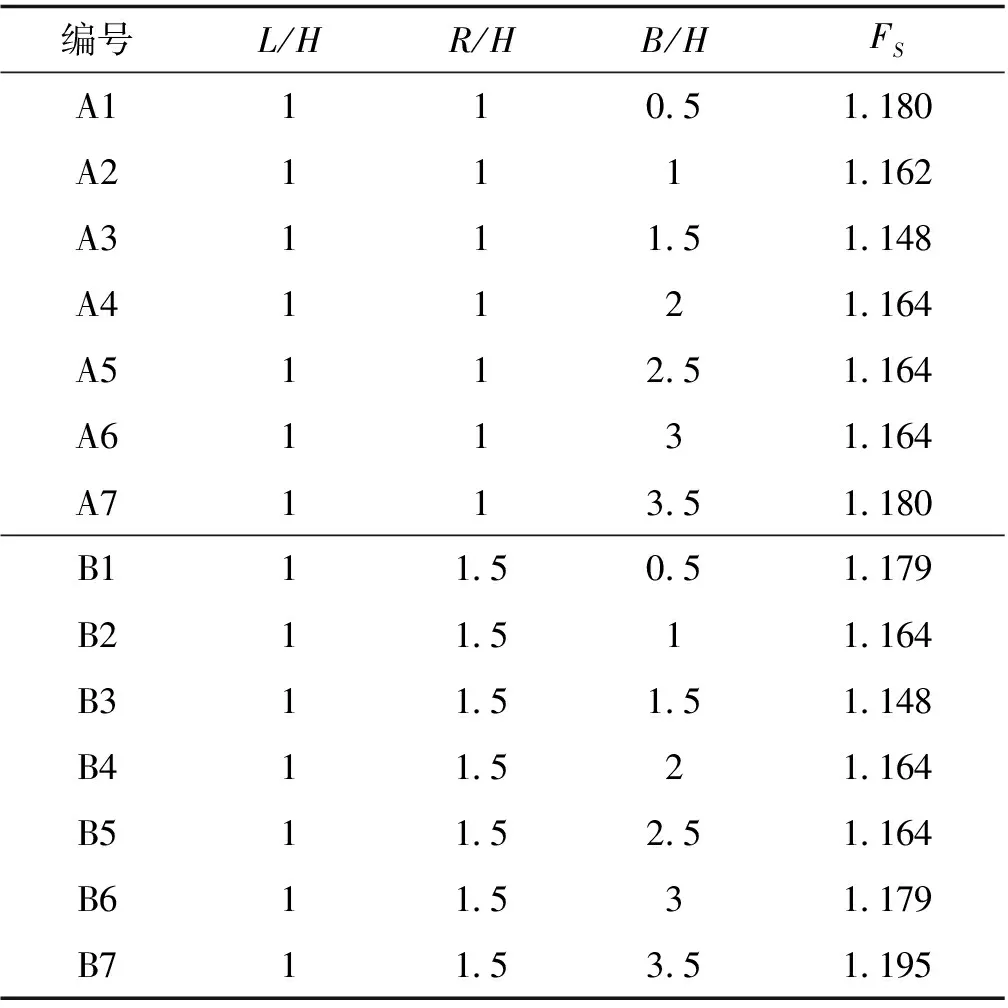
表4 坡體底部邊界大小對計算結果的影響

在左側邊界取值H、底邊界取值1.5H時，右側邊界分別取值H和1.5H的模型運算平衡狀態下的剪應變增量云圖見圖3。從圖3可知，右側邊界取值H時的剪應變增量比取值1.5H時的剪應變增量小，且后者的剪應變區域要比前者的大，但兩者的剪應變區均已由坡腳貫穿至坡頂，2種情況在這一點上差異很小。考慮到邊界越大，解算時間越長，建議右側邊界取值為H。

1.2 二維模型尺寸選用建議

等邊界取值建模時(即模型的左側邊界、右側邊界與底邊界的尺寸取值相同)，取3處邊界值均不小于1.5H時，結果較為可靠。在等邊界試驗所得結果的基礎上，以結果繼承的方式設計試驗，獲得分析模型左側邊界的最佳取值為H，右側邊界取值為H，底邊界取值為1.5H。此時，數值分析所得安全系數取值可靠且運算速率快。

(a) L=H，R=H，B=1.5H

(b) L=H，R=1.5H，B=1.5H

2 數值模型三維效應分析

為得到三維數模計算精度與運算速度之間的平衡點，在二維數模分析結論的基礎上開展三維模型尺寸效應的分析研究。相比較于二維數模分析情形，模型三維效應的區別主要體現在模型寬度對數值分析結果的影響上。設計如下試驗：模型左側邊界取值H(本次分析過程中H=20 m)，右側邊界取值H，下邊界取值1.5H，模型寬度從1 m(0.05H)逐漸增加至70 m(3.5H)，作為對照，坡角分別為27°、45°、63°三種情形進行試驗，模型下邊界完全約束(無自由度)，左右側邊界法向約束(只能在上下方向上發生位移)，與y軸垂直的邊界也采用法向約束，模型上部為自由邊界。計算過程中采用的土體參數均與二維試驗的土體參數相同。數模試驗分析結果見表5。

從表5的計算統計數據可得出，三維數模的寬度對計算結果有一定影響，在不同坡角情況下，隨著模型寬度的增加，安全系數均逐漸增加并最終趨于穩定。對于邊坡寬高比為2∶1(坡角為27°)的情形，當模型寬度取值大于等于H(20 m)時，坡體安全系數取值趨于穩定為1.709，相較該坡比情形下的二維模型(寬度為0.05H)，計算結果的偏大約4.8%。對于邊坡寬高比為1∶1(坡角為45°)的情形，當模型寬度取值大于等于1.25H(25 m)時，計算所得安全系數趨于穩定為1.258，與該坡比下的二維模型計算結果相比較，計算結果的偏大幅度達到了9.6%。對于邊坡寬高比為1∶2(坡角為63°)的情形，三維模型計算結果與二維模型結算結果的最大偏差達到了8.5%。因此，三維模型的構建寬度及坡比均對分析結果有一定影響。

表5 模型寬度變化對安全系數的影響

3 結論

1) 二維數值模型邊界尺寸對分析結果的影響受坡角的影響，坡角小于30°和大于60°時，邊界效應對分析結果的影響不明顯，坡角取值45°時，分析結果對邊界效應最敏感。二維模型的左側邊界、右側邊界及底邊界的取值均小于坡高H時，邊界約束效應對計算結果的影響較大，計算結果的準確性較差。當左側邊界與右側邊界均不小于H、底邊界不小于1.5H時，計算結果較為可靠。

2) 三維模型解算結果普遍大于二維模型解算結果，隨著三維模型寬度的逐漸增加，計算所得安全系數呈遞增收斂趨勢，收斂速度受坡角的影響，坡角越小收斂越快。若左側邊界、右側邊界、底邊界分別取值H、H、1.5H，對于坡角小于45°的情形，模型的寬度取值應不小于H；對于坡角大于45°的情形，模型的寬度取值應不小于1.5H。