一種關于“判知結論浮動”現象的多元主義解釋框架

徐英瑾

判知結論浮動（epistemic shift，直譯為認知浮動）是西方知識論文獻的一個常見說法。這個略顯拗口的詞組描述的是這樣一種現象：一個認知主體持有的某信念，在某些條件下被知識裁判人（knowledge ascriber）判定為“知識”，而在另一些條件下被判定為“非知識”。舉例來說：假設你是一位知識裁判人，現在請想象有個叫張三的人——他正看著自己一雙充滿老繭的手發呆。那么，你是否會裁定說“張三的確知道他有兩只手”呢？筆者相信大多數人會給出肯定的回答。這樣一來，“張三有兩只手”就是張三的“知識”的一部分。然而，在另一語境中，張三盡管在盯著他的手發呆，你卻被額外地告知：張三有可能就是一個“缽中之腦裝置”的犧牲品（根據“缽中之腦”的思想實驗，張三關于“自己有兩只手”的幻覺是通過一位邪惡的科學家精心刺激他的大腦皮層所產生的。除了一個被放置在營養缽之中的大腦之外，張三就沒有身體的其余部分）——在這種情況下，你是否會依然裁定說“張三的確知道他有兩只手”呢？恐怕這時候你的裁定就不會那么斬釘截鐵了。換言之，在引發“缽中之腦”之類的懷疑論思維的語境中，原本可以被判定為知識的信念，卻無法被判斷為知識。這就是所謂的“判知結論浮動”現象。

那么，我們究竟該如何解釋這種判知結論浮動現象呢？不同的哲學家提供了不同的理論方案。例如，著名哲學家劉易斯（David Lewis）、亞利桑那大學的科恩（Stewart Cohen）、耶魯大學的德羅斯（Keith DeRose）等語境主義者（contextualist）［1］（P91-123）［2］（P913-929）［3］［4］（P549-567），以及像羅格斯大學的夏佛（Jonathan Schaffer）這樣的比對主義者（contrastivist）［5］（P73-103）均認為，判知結論浮動現象之所以發生，是因為知識裁定活動本身是敏感于那些可以為知識裁判人獲知的語境信息的。也就是說，只要人們對“知道”的語義理解跟著語境變了，判知結論浮動現象也會隨著發生。至于像斯坦利（Jason Stanley）［6］這樣的“基于利害的不變主義者”（stake-based invariantists），則不是這樣看問題的。他們在解釋這一現象的時候，會訴諸那些與認知主體相關的因素，比如認知活動牽涉的旨趣與實踐方面的利害關系。對于同類現象做出不同解釋的還有“智性不變主義者”（intellectual invariantists），代表人物有多倫多大學的內格爾（Jennifer Nagel）。她主張運用與認知場景中的主體（而不是故事外的知識裁判人）自身相干的心理要素來解釋判知結論浮動現象，而她采用的具體解釋資源則來自心理學概念“固知需求（need-for-clo‐sure）”［7］。

不過，與某些讀者的預期可能相反，筆者不會在上述立場中選邊站，不會簡單地提出一種新立場來反駁上面的任何一種理論。毋寧說，本文將構造一種大一統框架，以便在重構上述各種理論的基礎上吸收其精華。而且筆者將說明，如果吾輩要以一種先天的方式來研究判知結論浮動問題的話，為何上述這種大一統框架乃是吾輩所能期盼之最佳結果。換言之，從元哲學的角度看，對于判知結論浮動的恰當哲學說明，必須容忍關于判知結果之沉浮的多種解釋的多元性，以顯示其應有的“海乃百川”的特征。而任何一種想在這些多元因素中凸出一點而不顧其余的做法，均會使得自己落入盲人摸象之境地。

一、導論：從“概率”含義的澄清說起

本文將利用特定的概率論規則（貝葉斯定理）構建大一統框架，理由在于：貝葉斯定理等概率規則都表達了特定的先天真理，對于它們的調用不太會遭遇明顯的爭議。所以，這些概率規則也就非常適合打造一個中立的理論框架，以供品鑒各種不同的知識論理論。

筆者注意到，此前已經有澳大利亞天主教大學的霍桑（John Hawthorne）和希伯來大學的克瓦特（Igal Kvart）兩位學者做出了類似的嘗試。他們在構建知識論框架時也將“知道”這一概念與概率論相聯系（順便說一句，英文中knowing與knowledge分享共同的詞根，對于“知道”條件的討論，基本等同于對于“知識”條件的討論）。那么，筆者的框架與他們的工作又有哪些區別呢？

第一，筆者與那兩位學者關于“概率”的定義不同。在克瓦特的理論中，概率既不是主觀概率，也不是相對的概率，而是所謂的“客觀的機遇”。他認為“概率”所刻畫的，是在給定世界先驗歷史（a priorhis‐tory of the world）的情況下，出現某個經驗事實發生之機遇［8］（P6）。而且，“世界的先驗歷史”是完全外在于知識裁判人的，是純客觀的。與之類似，霍桑也采用了客觀主義版本的“概率”概念［9］（P28）。但是，在筆者看來，在知識論研究中運用這種客觀主義色彩濃郁的“概率”觀，不太妥當。正如羅格斯大學的古德曼（Alvin Goldman）所指出的，解釋“知道”的含義基本相當于解釋大多數人關于“知道”的語言直覺［10］（P199）。這在很大程度上屬于心理學的范疇，與客觀世界所具有的先天歷史無太直接的聯系。古德曼的描述中已經出現了一種打通心理學研究和知識論研究的傾向，這一傾向亦在內格爾的工作中被大大強化［7］。她直接采用心理學概念“固知需求”作為具體解釋資源——順便說一句，在心理學領域，該概念的提出者乃是克魯格斯基（Arie Kruglanski）與韋伯斯特（Donna Webster）［11］。秉承古德曼、內格爾兩人的精神，筆者使用的“概率”概念也是主觀主義的。

第二，筆者與克瓦特、霍桑兩位學者關于“概率”概念的適用范圍不同。克瓦特的理論主要處理知覺知識［8］（P3）。筆者的理論不僅可以解釋那些牽涉知覺知識的場景，還可以容納諸多別的場景。

第三，筆者與克瓦特、霍桑兩位學者各自的理論立場所具有的“寬容度指數”不同。為了解釋日常生活中的知識評判現象，霍桑在其知識論構建中引入了所謂的“摩爾式的知識限制條件”［9］（P111），眾所周知，G·E·摩爾乃是一位以尊重日常生活中的常識判斷為著稱的哲學家。但是，既然霍桑引入了摩爾式的知識限制條件，也就引入了一種接近于摩爾主義的常識主義立場，這種立場不可能兼容其他關于判知結論浮動的理論立場。與之相比，筆者的理論對所有立場保持中立，以超然的態度來評判各種不同的理論。

筆者無意給出一個完整的關于“知識”的定義，僅僅試圖給出一種如何解釋判知結論浮動現象的理論。有限的理論目的，將能夠使筆者僅僅關注“知識”構成的必要條件，減少理論構建的負荷。

二、用概率論刻畫“知”之底線

毫無疑問，要羅列“知識”得以成為知識的充分必要條件，是非常麻煩的。在知識論的研究史上，已經有太多人做出過努力，目下依然沒有哪一項關于“知識”的定義得到學界的普遍贊同。既然本文的目的是去說明判知結論浮動現象，筆者就可以由此合理規避全面定義“知識”的任務，而只需要聚焦知識構成的某個必要條件，并把它設定為“知”之底線，一個信念至少應當先滿足該底線所提出的要求，才有可能成為知識。這種研究思路來自木桶效應——木桶的水位取決于圍成木桶諸木板的最低那塊的高度，我們可以通過討論那塊最關鍵的（它往往就是最低的）木板的高度來討論木桶的水位。同理，我們也可以通過對于某條“知”的底線高低的討論，來介入判知結論浮動現象的討論。

我們先對底線作粗線條勾勒。從一常識開始我們的探索：只有當一個主體所持有的信念是一個內容為真的信念時，我們才能說該信念是知識，或者說主體知道它。

例如，當一個小姑娘對你說，她知道“巴黎是英國的首都”，你一定不會覺得她真“知道”這一點，事實上倫敦才是英國的首都，“巴黎是英國的首都”是不符合事實的。說得抽象一點，要去判定某認知主體S是否“知道”某事P，至少需要檢查兩個條件是否滿足：其一，S本人是否相信P；其二，該信念P是否與外部事實P相符。如果S的信念和外部事實不相符，P就不是知識，任何一個知識裁判人也就不能說S知道P。在此，“外部事實P”就可以被稱為“P 的使真者（truth-maker，指對于使得內部信念為真的外部事實，下同）”。

現在我們就用“P內”指涉命題P在主體S心靈內部的信念表征，“P外”則指與P相關的外部事件。根據這樣的記號，我們得出一個“知之底線”的刻畫草案：

一個信念P被判斷為“知識”，至少得滿足條件：Pr（P外|P內）=1。

自然語言的翻譯就是：一個信念P被判斷為“知識”，至少得滿足的條件：在P內本身已經被認為是真的前提下，我們計算P外的后驗概率得到的結果是1。需要注意的是，討論P內約束下的P外的后驗概率，就等于討論“針對P內這一現象的基于P外的解釋的合理性”。舉例來說，針對張三擁有“倫敦在英國”的信念這一有待解釋的現象，我們搬出“倫敦的確就在英國”這一事實，是不是就能夠完美地完成解釋任務呢？如果草案里的概率值的確是取1的話，那么，問題的答案就是肯定的。

顯然，這個公式用概率學的語言，刻畫了前面提到的那條常識：只有當一個主體所持有的信念其內容為真時，才能說該信念是“知識”。

但我們還不能滿足于這種刻畫。按照上述刻畫方案，知識裁判人將會永遠將該主體的信念判定為知識，這樣也就不會出現判知結論浮動現象。為了解釋判知結論浮動現象，我們必須引入一個可以被度量的變量，而且這個變量恰好能夠影響知識判定的結論。基于上述考量，筆者引出“知之底線”的刻畫草案（改1）：

一個信念P被判斷為“知識”，至少得滿足條件：Pr（P外|P內）的值必須足夠高。

“足夠高”的確是一個含混的表達，但筆者是有意利用它的含混性，以包容不同的關于判知結論浮動的理論。

然而，這樣的刻畫還不能應對一些特殊的知識論案例，如下面的案例：有個名叫漢娜的小姑娘，還沒上過學，對現代化學一無所知。可是，當有人問她各種化學問題的時候，她回答的竟然都對，這是因為有一個萬事通小天使偷偷告訴她各種化學問題的答案了。假如信念P表示“一個甲烷分子是由一個碳原子和四個氫原子組成的”，顯然P在外部世界中是真的，即P外的值為1。在小天使的耳語下，漢娜又的確產生了信念P，而且相信P是真的，故此，P內的值為1。這樣一來，表達式Pr（P外|P內）的值應該也是1。根據前文的定義，作為知識裁判人的我們此刻應當判定漢娜知道關于甲烷的化學構成的知識。但是在直觀上，恐怕很多人未必會覺得漢娜知道這一點。不少人會傾向于說：真正知道化學知識的是小天使，而不是漢娜，后者只是鸚鵡學舌罷了。

即使面對上述反例，從純粹邏輯角度看，我們似乎還是能夠堅持關于“知之底線”的刻畫草案，因為該草案僅僅涉及“知道”的必要條件，而非充分必要條件。然而，僅僅從這個角度應對反駁，又會使得草案顯得過于粗糙而缺乏對于“知識”之本質的穿透力。因此，我們最好還是沿著上述反例提出的思路，細化草案。由此，讀者給出了修改方案“知之底線”的刻畫草案（改2）：

一個信念P被判斷為“知識”，至少得滿足條件：我們（知識裁定人）在評估Pr（P外|P內）值的時候，考慮到P（rX）的抵消作用，發現這個值依然必須足夠高。

那么，這里出現的X是指什么呢？筆者把X稱為“異常使真者”（Abnormal Truth-maker），也就是使得內部信念成真的外部因素中的異常者。這是相對于“常規使真者”（Normal Truth-maker）而言的。在漢娜接受化學測試的例子中，“一個甲烷分子在事實上的確是由一個碳原子和四個氫原子組成的”這一點，就是一個“常規使真者”。但漢娜沒接受過科學教育，這個使真者自身無法獨立地解釋她為何會具有甲烷構成的真信念。所以，我們就得引入一個“異常使真者”來解釋，此即那個天使的作用。“異常使真者”的出現，會使得知識裁判人更不傾向于認為漢娜是具有知識的，因此，我們就必須在考察Pr（P外|P內）值的時候，充分考慮Pr（X）的值——它其實就是“異常使真者”出現的先驗概率值——的大小，并將其作為干擾因素予以扣除。我們可以得到“知之底線”的刻畫草案（改3）：

一個信念P被判斷為“知識”，至少得滿足的條件：Pr（P外|P內）的值足夠高，且Pr（P外|P內）= 1- Pr（X）。

對于“Pr（P外|P內）= 1- Pr（X）”這一結論的概率推算如下：

先根據貝葉斯定理計算Pr（P外|P內）：

（1）Pr（P外|P內）= Pr（P內|P外）× Pr（P外）/Pr（P內）

要算出等式左邊的值，我們顯然要計算等式右邊諸項的值。P內的概率值必須是1（因為根據某種“準笛卡爾主義”的理論精神，內在信念的可靠性基本是不可懷疑的）。但是如何確定Pr（P內|P外）的值呢？筆者認為此值也是1。這是基于一種常識性的考慮，即與P相關的事實在通常情況下會產生與P相關的真實信念。

由（1）可得（2）：

（2）Pr（P外|P內）= 1 × Pr（P外）/1= Pr（P外）

那么，我們又該如何確定Pr（P外）值？筆者建議采用“全概率公式（Law of total probability）”，據此，得到：

（3）Pr（P內）=1= Pr（P內|P外）× Pr（P外）+ Pr（P內|X）×Pr（X）

=1 × Pr（P外）+1 × Pr（X）

=Pr（P外）+ Pr（X）

據此，

（4）Pr（P外）=1-Pr（X）

結合（2）與（4），得到：

（5）Pr（P外|P內）= 1-Pr（X）

當然，可以降低Pr（P外|P內）值的“異常使真者”的數目可能不止一個。考慮到這一點，上述草案應被升級為“知之底線”的刻畫草案（改4）：

一個信念P被判斷為“知識”，至少得滿足的條件：Pr（P外|P內）的值足夠高，且Pr（P外|P內）(Xi)（n≤N）。

對于上述公式的自然語言表達：在關于P的內部表征已經被確定的情況下，該內部表征的知識地位的穩固度，等于1減去所有使得P內得以產生的“異常使真者”的概率之和后的余數。此處，N指知識裁判人所能想到的異常使真者的最大數目。如何確定N的值，與對于知識裁判人本人的工作記憶容量的評判結果相關。

根據“草案（改4）”可知，諸“異常使真者”對知識的顛覆力越大，知識裁判人就越不會傾向于把信念判定為知識，反之亦然。所以，對于判知結論浮動現象的討論就能被轉化為這樣一個問題：知識裁判人能想到多少個異常使真者，以及每一個異常使真者在知識裁判人眼中的知識顛覆力有多大。這些顛覆力的加權和，就是(Xi)的值。

語境主義者、比對主義者、基于利害的不變主義者和智性不變主義者都可能對筆者的這種貌似過于缺乏斷言內容的建議提出異議。他們可能不反對筆者對“異常使真者”的刻畫方式，但會進一步提出：我們應該聚焦于某個更重要的認知因素，以便更為細致地刻畫“異常使真者”對于知識的顛覆力。在語境主義者眼中，這個更重要的因素是“語境因素”［2］（P913-929）［3］（P1-52）；在比對主義者眼里，該因素便是“語境比對項（Semantic Contrast）”［5］，而在“基于利害的不變論者”眼中，該因素便是“利害關系”（Stakes）［6］，而在“智性不變論者”那里，該因素是“固知需求”（Need-for-Closure）［7］。

在筆者看來，所有這些理論都犯了以偏概全的錯誤。下面筆者先來批評語境主義。

三、透過“合理性”與“敏感性”概念重構語境主義

在一般的談話中，沒人會覺得自己是“缽中之腦”，而在哲學教師教授懷疑論的哲學課堂中，我們卻很有可能會懷疑自己的確就是“缽中之腦”。在語境主義者看來，之所以我們會對于“自己是不是缽中之腦”問題產生不同的答案，要害就在于：知識判定的語義標準會依語境而變化——在日常談話的語境中，這個標準是比較低的，而在引發懷疑論思維的語境中，該標準會被提高。那么，為何日常談話的語境與引發懷疑論的語境能夠各自提出不同的知識標準呢？對于該問題，不同的語境主義者的解答方案是彼此不一樣的。比如，根據亞利桑那大學的科恩教授的觀點，這主要取決于一個相關的“異常使真者”所具有的合理性程度究竟有多高［1］；而耶魯大學的德羅斯教授認為這牽涉到我們的目標信念自身所具有的敏感性的程度都有多大［3］。

先討論科恩的想法，那是基于合理性的語境主義：

當且僅當如下的條件被滿足時，對于目標信念P而言，對于該信念的一個異常使真者h必須要被知識裁判人所考慮到：即在特定理由r被給定的情況下，h自身所具有的后驗概率必須足夠高。其中，“足夠高”的標準則取決于特定的語境的規定［1］。

舉例而言：假設目標信念P是“我看到了一個看上去是斑馬的動物”。對信念P來說，有兩個競爭解釋：一個解釋表征了“正常的使真者”，即我眼前真有一匹斑馬。另一個解釋由“異常使真者”提供：我所看到的并非是斑馬，而是被精心涂抹成斑馬的騾子。那么，對于知識裁判人來說，“我所看到的只是一頭被涂成斑馬花色的騾子”這個假設，是否應該被考慮呢？這取決于在給定動物園的環境和知識裁判人已知的信息的情況下，該假設自身成真的后驗概率有多高。如果它的后驗概率高過了一定的閾值，這個解釋就是相關的，應當被納入考慮范圍。閾值有多高，由語境本身來決定。

科恩的描述已經頗具概率論色彩，可以被輕易順化為筆者的解釋框架。略為麻煩的是對基于“敏感性”概念的語境主義的概率化重述。

什么叫“敏感性”？這個概念是美國哲學家諾齊克（Robert Nozick）提出的。根據他的看法，若一個主體S是以具有“敏感性”的方式去持有信念P的，那么這就能保證S是的確知道P的。“敏感性”條件之被滿足，當且僅當如下條件被滿足：只有在P自身是真的情況下，P才能夠被S所相信——反之，如果信念P本身非真，那么主體S就不會相信P［12］。譬如，如果法國的首都的確不是柏林，那么，張三就不會相信法國的首都是柏林；如果張三的確不是缽中之腦，則張三就不會相信自己是缽中之腦。從這個意義上說，S的信念是敏感于P自身的真值的，并與其有“隨動關系”（P的成立對應于S關于P的正向信念，而P的不成立則對應于S關于P的否定性信念）。德羅斯在表述他自己的語境主義概念時，利用了諾奇克的“敏感性”概念，這是基于敏感性的語境主義：

當我們要確定某個主體S知道或不知道某個命題P時，在某些必要的情況下（特指懷疑論語境出現的情況——引者注），知識的標準就會提高到這樣的水平：主體S對于命題P的擁有方式必須具有敏感性，以便使得這個信念P本身能夠被視為知識的一部分［3］（P36）。

乍一看，德羅斯的上述說法沒有涉及概率學的術語，很難被順化為筆者的表述框架。這里的一個明顯技術麻煩是：傳統上用來描述敏感性的技術框架乃是“可能世界語義學”，而非概率論。但筆者依然認為這種順化乃是可能的。很明顯，用概率論的方式來直接表征敏感性，我們就必須訴諸Pr（~P內|~P外）的值（該公式的意思是：相應外部事實P自身不存在的情況下，相應的內部表征也不存在的后驗概率）。這個值應當比較高（非常接近1），以便表示這樣的一個想法：相應外部事實P自身不存在的情況下，相應內部表征也不存在的可能性也非常高。這便構成了對于“敏感性”的下述含義的改寫：

當P自身非真時，S就基本上會去相信“非P”。

那么，如何進一步確定“Pr（~P內|~P外）”自身的值非常高的條件呢？我們不妨先利用貝葉斯定理來計算Pr（~P內|~P外），可得：

（6）Pr（~P內|~P外）=Pr（~P外|~P內）×Pr（~P內）/Pr（~P外）

為了計算等式右邊的值，我們需要先確定Pr（~P內）和Pr（~P外）的值。兩者均包含了否定性表征，或者說，均涉及了對于否定性事件的概率的賦值。那么，此類事件的概率究竟該如何賦值呢？筆者認為這不是一個容易解決的問題。正像蒯因（W.V.Quine）指出的，以否定性的方式得到表征的表達式——比如“非烏鴉”——是無法直接對應于世界中的自然類的，而是人為約定的產物［13］。換句話說，人們可以隨機確定某物為“非烏鴉”，比如桌子、電腦、布谷鳥，等等，而這些事物之間并無正面的共享特征將其連接到一起。這種做法顯然將導致指稱的含混性。要清除這種含混性，我們就必須對此類否定性表征所留下的邏輯空間包含的事物進行更加細致的區分。舉例而言，我們若想要計算“不下雨”的概率，實際上我們就得計算“天晴”“多云”“下雪”等所有能夠被歸類為“不下雨”事件的概率的析取值。為了計算一個否定性事件的概率，我們就不得不計算一系列能夠被囊括為該否定性事件的所有的正面的子事件的概率。這也是我們在以概率論的術語刻畫“敏感性”時不得不采用的策略。

在進行了此番的操作后，“非P”之類的表達，就必須被兌現為一個個以正面方式得到表征的子事件。這些子事件的數量是海量的——譬如，對應“并非我眼前有一匹斑馬”這個否定性的表達，就會有無數個以正面形式出現的命題：“我眼前有一頭駱駝”“我眼前有一個外星人”，等等。但并非所有的命題都與懷疑論的哲學困惑有關，因為懷疑論的肯綮在于：任何一個既具有“非P外”的血統，又不具備“非P外”之外觀的、并以正面形式被表述出來的命題，恰好能夠用來解釋“P內”在認知主體表征系統內部的生成。也正因為這一點，認知主體才會在該解釋與基于“P外”的“正常解釋”之間反復踟躕，懷疑再三。這一點當然就會導致“Pr（P內|~P外）”的值與“Pr（P內|P外）”的值彼此大約相等（大約都是50%），讓人無法找出優勝者。這也會導致整個“Pr（~P內|~P外）”的值——這也就是對于“敏感度”的度量值——的降低。從概率學的角度看，如果“Pr（P內|~P外）”的值接近50%的話，“Pr（~P內|~P外）”的值是不可能接近1的（好比說，如果你知道不下雨會將人渴死的概率只有50%的話，你是無法從中推出同等條件下人不渴死的概率是接近1的。后者的值應當也接近50%才對）。這也就是說，懷疑論的語境，就是那些使得“Pr（~P內|~P外）”的值得以被明顯降低的語境。

在這些懷疑論語境中出現的任何一個既具有“非P外”的血統，又不具備“非P外”之外觀的、并以正面形式被表述出來的命題，既然都能用來解釋“P內”在認知主體表征系統內部的生成，它們就是使得“P內”為真的“異常使真者”，它們的“知識顛覆力”——在此就是指“敏感性顛覆力”的大小——可以通過對于的值的估量而得到判定。由此，語境主義的話語框架，也就被順化為筆者的話語框架。

四、“異常使真者”如何在語境主義的框架中被甄別

在上節中，筆者僅僅是在形式上把科恩和德羅斯的語境主義敘述方式順化為筆者的敘述方式，但不意味著語境主義本身是一種站得住腳的立場。筆者對語境主義的疑慮在于：他們是否提出了一些相應的規則，以說明為何某些“異常使真者”需要我們在考慮懷疑論的問題時被加以考量，而有些則不需要被加以考量？就筆者所知的范圍內，在該問題上給出最系統思考的語境主義者乃是大衛·劉易斯（David Lewis）。他提出了一系列規則，用以甄別出哪些“異常使真者”是不能被忽略的［4］。筆者在此僅僅提到二者，一是保守主義規則：

那些從常識角度看，不能被忽略的“異常使真者”是不能被忽略的。

譬如，如果你生活在一個假斑馬充斥的世界中的話，那么“假斑馬很多”就會成為你的常識的一部分。這樣一來，“你看到的所謂斑馬就是被精心涂抹的騾子”的那種可能性就不能被忽略［4］（P559）。不過這也就意味著：那些從常識角度看可以被忽略的“異常使真者”，大約是可以被忽略的。

二是注意力規則：

那些在特定的談話語境中，的確引發談話人之注意的“異常使真者”乃是不能被忽略的［4］（P559）。

舉例來說，在哲學教師教授懷疑論思想的課堂上，“缽中之腦”的假設如果的確引發了同學們的興趣與注意的話，那么，在解釋“為何我看上去有兩只手”這一點時，同學們就無法忽略“這一信念是由一臺復雜的缽中之腦裝置所引發”這一異常的解釋。

筆者的擔憂是：這兩條規則似乎互相打架。“注意力規則”實際上具有求新、求異的意蘊，故此新聞界才有諺語說“狗咬人不是新聞，人咬狗才是新聞”。但“保守主義規則”則具有反向的意蘊，該規則不鼓勵大家天馬行空地胡思亂想。譬如，除非“缽中之腦”的案例的確已經大量出現在了生活之中，并成了我們常識的一部分，否則，在知識論討論中引入基于該案例的“異常使真者”，就是白費力氣。

從論證的責任來看，究竟該如何順化上述這些規則的關系，乃是語境主義者自己的事情。但在他們澄清這一問題之前，我們不妨就可以認為語境主義在不少重要細節方面具有瑕疵。與之相比較，筆者對于“判知結論浮動”的一般性解釋框架就不用承擔這種解釋負擔。道理是非常簡單的：筆者的解釋框架只是用來展示各種關于“判知結論浮動”的特定理論的一種中立性平臺，缺乏細節不是對該平臺的合適指控。

下面我們重述并評估別的關于判知結論浮動的特定知識論理論，以“基于利害的不變主義”為例。

五、重估“基于利害的不變主義”

“基于利害的不變主義”或“與利害相關的不變論（Interest-Relative Invariantism）”是指這樣一種立場：相關的認知主體是否會將一個目標信念視為知識，在相當程度上與此類賦知活動帶給他的實際好處或者壞處有關。具體而言，當相關主體的現實利益處于高風險時，其做出錯誤判斷所要帶來的代價也較大，這樣一來，我們就更難說該主體所持有的相關信念P乃是知識的一部分，反之亦然。

若用筆者的模型來表達，上述立場就相當于以下兩種說法的結合：

（甲）“草案（改4）”是成立的，即：Pr（P外|P內）=

（乙）對于任何一個解釋“P內”的備選性解釋而言，當且僅當有足夠的利害關系與之牽扯時，它才值得被填入“Xi”槽中。在此“Xi”是指那些有特定的利害或興趣與之相關的“異常使真者”。

本節所談的這種立場的意蘊，可以通過“銀行案例”來加以說明。假如張三背著巨額房貸，而且，張三還相信每月最后一個周日是當月還貸的最后期限。現在再假設有兩種可能引發了他的這個信念：其一，該信念是基于他對于銀行還貸日的正確的記憶；第二，該信念是基于他對于銀行還貸日的錯誤的記憶。假設張三的財務情況非常好，那么即使他搞錯了還貸的日子，他的信用記錄也不會因此而留下污點。這樣一來，“錯誤記憶”這一“異常使真者”所導致的知識削弱力就不會太大，并因此可以被忽略。反之，如果張三的財務情況是入不敷出的，那么，及時還貸就會對其征信記錄的清白產生莫大的影響。在這種情況下，“錯誤記憶”這一“異常使真者”所導致的知識削弱力就會被放大，并因此無法被忽略。這也就是說，在張三本身的財務風險不大時，“草案（改4）”中“”的值會變得很小，“” 的值就會隨之較大，而“Pr（P外|P內）”的值也相應會變得較大。這樣一來，張三的相關信念就更容易被判定為知識的一部分。但是，如果張三的信用風險很高，那么，“草案（改4）”中的值就會隨之變大，的值就會隨之變小，而“Pr（P外|P內）”的值也會隨之下降。這樣，張三的相關信念就更難被判為知識的一部分。

由此看來，“基于利害的不變主義”是可以被順化為筆者的模型的某種變體的。

但這種學說本身卻依然是有問題的。正如羅格斯大學的夏佛（Jonathan Schaffer）所指出的，“基于利害的不變主義”無法處理類似缽中之腦等懷疑論案例［14］（P87-107）。舉個例子：在張三看著自己的兩只手的時候，他是否知道自己有兩只手呢？在這個問題中，“我有兩只手”這個信念被“缽中之腦之類的裝置所引發”這種可能性是否應該被忽略呢？在哲學課堂上，這種可能性大概率是不應被忽略的。但這并不因為“缽中之腦”這種設想與張三有任何利害關系，而僅僅是因為我們在理論上不應忽略這種可能性。從這個角度看，“基于利害的不變主義”無法處理懷疑論等案例，因此，該立場不具備普遍可應用性。

上述的批評甚至還可以被施加到對于施羅德（Mark Schroeder）對于斯坦利的“基于利害的不變主義”的改進方案之上［15］。他的改進方案的核心思想是：

只要下述條件被滿足，那么，S相信p的理由就至少與S相信~p的理由一樣充足：

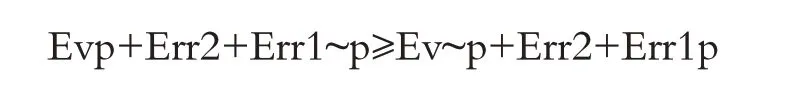
這個公式的意思是：S用以支持p的證據強度、S犯下“乙型錯誤”的代價以及S犯下“相信～p的甲型錯誤”的代價之和，必須大于或等于S用以支持～p的證據強度、S犯下“乙型錯誤”的代價以及S犯下“相信p的甲型錯誤”的代價之和（這里所說的“甲型錯誤”是指“將某個命題的真值搞反的錯誤”，“乙型錯誤”則是指“將某類事項完全忽略的錯誤”）。

對于施羅德的上述意見，筆者的反駁是：他是否提出了某種統一的量綱，以便我們去統一地計算“S用以支持p的證據強度”“S犯下乙型錯誤的代價”等變量的值呢？如果施羅德無法給出這種計量方法的話，那么，他的方案就無法具有真正的普遍適用性。

在下文，筆者將考察“不變主義”的另一個變體——“智性不變主義”。

六、重估“智性不變主義”

根據內格爾的“智性不變主義”觀點，“判知結論浮動”現象不能通過主體所處的環境要素來解釋，而應通過主體內部的信念形成過程來描述［7］。這就牽涉到“固知需求”這一心理變量。

心理學家克魯格斯基和韋伯斯特將“固知需求”定義為：在一個特定的話題上，心理主體有特定的心理需求，而將某些信息固定為知識。固知需求這一心理學變量既能體現出個體差別（比如有人在固定知識的過程中顯得性急，有人則顯得拖沓），也能夠體現出環境差異（比如同一個人在某些環境下會傾向于立即給出問題的答案，在有些環境下會舉棋不定）［11］。

內格爾用固知需求重新解釋了前文提到的銀行案例，大意是：一個人的財務風險越高，其搞錯銀行還貸日帶給他的潛在麻煩就越大，因此，他也就有更多的理由去反復檢查還貸日期是否真被搞錯了。在這樣的情況下，他的固知需求就會變得比較小，而他做出有銀行還貸日的知識指派的效率也會被降低。反之，一個人的財務風險越小，其搞錯銀行還貸日帶給他的潛在麻煩就越小，因此，他也就缺乏更多的理由去反復檢查還貸日期是否真被搞錯了。在這樣的情況下，他的固知需求就會變得比較大，而他做出有關于銀行還貸日的知識指派的效率也會被提高［7］（P289）。

盡管內格爾描述的固知需求似乎只與利害關系相關，但實際上她提到了其他幾個影響固知需求的因素，比如時間壓力、疲勞程度、背景噪音，等等［7］（P288）。她沒有提供一個統一的模型來解釋這些因素是如何彼此融合、相互協調的，但至少她的確對判知結論浮動的動力因機制采取了一種多元主義觀點。這與筆者的模型所隱含的多元主義思想頗為接近。內格爾的理論可以通過筆者的模型被重構如下：

（甲）“草案（改4）”是成立的，即：Pr（P外|P內）= 1

（乙）對于任何一個解釋P內的“候選使真者”，當且僅當它附帶一個比較低的“固知需求”的值時，它才值得被填入Xi槽中。

在筆者看來，內格爾的理論還是不夠多元性，她忽略了一些在原則上無法被還原為固知需求的要素——這些要素對于解釋判知結論浮動現象來說，的確是頗為重要的。筆者想到的這一被內格爾所忽略的要素，與知識裁判人自身的社會角色轉變頗為相關。

為何要考慮這一要素呢？

古德曼就曾提出，在面對“缽中之腦”之類的玄想時，經過良好訓練的哲學從業者會比普通人更快入戲。即使在面臨一個日常生活中的信念時，哲學家或哲學系的學生也會比一般人考慮更多的“異常使真者”［10］。從這個角度看，作為一種社會現象，哲學教育的功能便體現于：它能夠幫助從業者迅速從日常的思維頻道切換到哲學的（特別是懷疑論）思維頻道。

筆者認為古德曼的考量頗有道理。但他的這段評論卻給內格爾的理論帶來了麻煩，因為古德曼所談到的關涉到社會角色轉變的要素，是無法被順化為固知需求的。為何這么說呢？

關鍵在于“時間”這一變量。眾所周知，任何的心理過程的展開，包括知識判定活動，都需要花費時間。對于一個受良好訓練的哲學從業者而言，在進行知識判定時，他只需要消耗非常少的時間，就可以從普通人的思維模式迅速切換到哲學從業者的思維模式，由此熟稔地處理“缽中之腦”的懷疑論案例。

另外，按照內格爾的理論，對于“缽中之腦”這類案例的研究卻顯然需要降低固知需求，以便為主體爭取更多的時間來評估相關“異常使真者”的合理性。這樣一來，面對同一案例，相關評判人的社會角色轉換所需時間越短，其固知需求就會隨之降低，導致判知時間延長。因此，社會角色的快速切換所導致的時間消耗量，與固知需求所導致的時間消耗量，在量的特征方面彼此相反。與社會角色切換相關的要素就很可能是固知需求之外的一個獨立要素，不能被簡單還原為后者（好比說，當你在檢查一個宏觀的經濟運作體系的時候，如果有某種生產模式被發現一直在增加碳排放量，另外一種生產模式則一直在削減此類排放，那么，這兩種模式就極可能是彼此獨立，而不可被彼此還原）。但內格爾的模型沒有提到這一獨立要素，那么，她關于判知結果浮動效應的解釋模型就是有所遺漏的。與之相比，筆者的理論模型沒有對任何導致判知結果浮動效應的特定解釋進行偏袒，也就不存在遺漏某項特定要素的問題。

七、結 論

語境、利害關系、固知需求等要素都對判知結論浮動現象有所影響，但它們都只強調了現象得以發生的某個特殊方面。語境主義者無法說明如何恰當地甄別那些值得關注的“異常使真者”；“基于利害的不變論者”則無法恰當地處理那些沒有明顯的利害牽扯的懷疑論案例；至于基于“固知需求”的智性不變主義者，則無法解釋那些不可被還原為“固知需求”的社會因素在知識指派中的作用。針對筆者對于上述立場的批評，有人也可以反駁說：我們為何不能找到更多的影響判知結論浮動的要素，全面升級前面的理論呢？筆者對此建議的回復是：升級雖然在邏輯上可行，但被涉及的因素越多，模型就會包含越多的語言學、心理學或社會學成分，最終使得相關的理論模型具有更強的實證科學氣味，而由此遠離哲學。如果想停留在哲學層面上討論相關問題，我們就只能滿足于刻畫判知結論浮動何以可能的諸要素的形式特征。這也是本文概括出來的“草案（改4）”完成了的工作。該模型既能提供一些關于判知結論升降的先天真理（并因此足夠哲學化），又對所有現有的關于“判知結論浮動”現象的經驗性解釋保持中立（并因此足夠海納百川），實為哲學家所能期盼的關于此現象的最終解釋了。