人致振動載荷下樓蓋結構的瞬態動力學分析
付章建, 岳祖潤
(1.石家莊鐵道大學 土木工程學院,河北 石家莊 050043; 2.河北省建筑科學研究院有限公司,河北 石家莊 050021; 3.石家莊鐵道大學 省部共建交通工程結構力學行為與系統安全國家重點實驗室,河北 石家莊 050043; 4.石家莊鐵道大學 道路與鐵道工程安全保障省部共建教育部重點實驗室,河北 石家莊 050043)
隨著建筑行業的不斷發展,工程師在設計建筑結構時,綜合考慮了建筑結構的安全性、適用性、耐久性、美觀性等因素的影響,使設計出來的結構可以滿足工程的基本需求。但是,在使用過程中有時會出現由于建筑物振動過大,使得建筑物在使用年限內出現由于共振引起的安全性問題。因此,近年來人們對建筑結構在服役期間的振動問題進行了廣泛研究,尤其是人致振動作用下的橋梁結構[1-3]和大型公共場所樓蓋結構,世界各國普遍采用健康監測的方法實時監測建筑物狀態,并通過主動或者被動控制方式對建筑結構產生的振動進行控制[4-7],保證建筑物在使用期限內的安全性。學者們在結構動力學方面進行了深入的探索,取得了豐碩的成果。文獻[8-10]從舒適度方面提出了改進的方法,提高了人行橋的振動舒適度;文獻[11-14]通過數值仿真,分別對過街天橋、登機橋、地板、人行過道結構進行了計算分析,總結了所研究結構的人致振動規律;De[15]通過實驗方法揭示了在各種人致荷載作用下,復合材料樓板的動力性能;文獻[16-21]采用多種人致振動激勵方式,對引起的樓蓋振動響應的影響因素進行分類分析;An等[22]對弦支組合樓蓋結構進行了人致振動分析,并進行了多載荷工況下的的現場試驗,表明該結構受到多種載荷作用明顯。上述研究多局限于對整個建筑結構的簡單理論求解或者模態分析,對結構中樓蓋各個響應點的動力特性研究分析相對較少,而工程中不同使用功能的樓蓋對于結構動力特性的要求不盡相同,結構的響應規律也各異。
本文以河北省衡水市桃城區某小學體育館為工程實例,通過實驗測試和有限元驗證的方法,以一層樓蓋局部混凝土樓板為研究對象,采用人致振動激勵,通過單點拾振獲取所測樓板各測點的振動響應速度,分析在跳躍和屈伸運動激勵作用下的樓蓋動力學速度響應情況,對比并總結了2種工況下樓板的能量傳遞形式、機理及其響應規律。
1 測試樓蓋結構及實驗設計
本次測試結構為河北省衡水市桃城區某小學體育館樓蓋,該結構為地上2層的混凝土框架結構,一層為梁板式樓蓋,平面布置圖如圖1所示。本次測試區域為樓蓋中部區域,測試區域橫向跨度10.35 m,縱向跨度15 m,橫向主梁截面尺寸為300 mm×650 mm,縱向主梁、次梁截面尺寸均為250 mm×600 mm,柱子截面尺寸均為400 mm×400 mm,樓板為現澆樓板,厚度為110 mm,結構梁、板、柱混凝土強度等級均為C30。
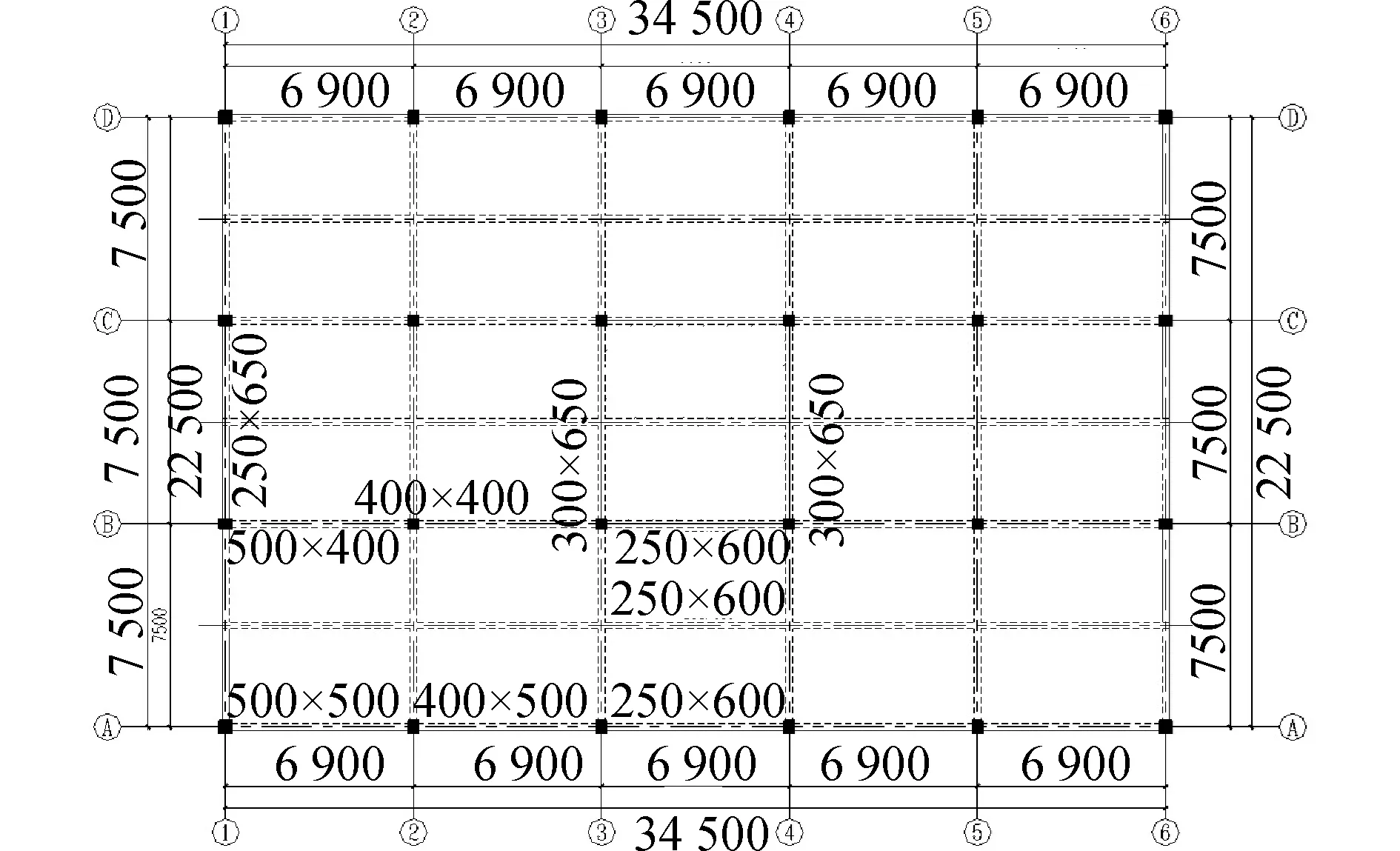
圖1 一層樓蓋平面布置Fig.1 The plane layout of the first floor
樓蓋結構響應作為結構分析的一個重要特性,能夠系統地反映整個樓蓋的各項指標,通過對各個指標的詳細分析,可以對樓蓋的動力學性能進行預測,判斷樓蓋結構的振動特性,進而可以從減振角度實現優化結構形式的目的。通過樓蓋的結構動力響應實驗分析,可以得到樓蓋各個位置處的速度值,進而可以驗證理論計算結果準確性。
樓蓋板構件作為連續彈性體,當在不同位置進行激勵時,響應各點的振幅不同,往往從激勵點向周圍呈輻射狀分布。為了準確測量響應信號,振動測試方向應與結構樓板的垂直方向(法向)一致,將測點在沿橫梁和縱梁方向上,分別等間隔布置。對于板構件的振動測試,測點數量不應少于5個,通過同步測量14個測點的響應,對比不同激勵狀態下樓蓋結構的動力學響應規律,以期得到良好的測試效果,1~14號測點布置圖如圖2所示。
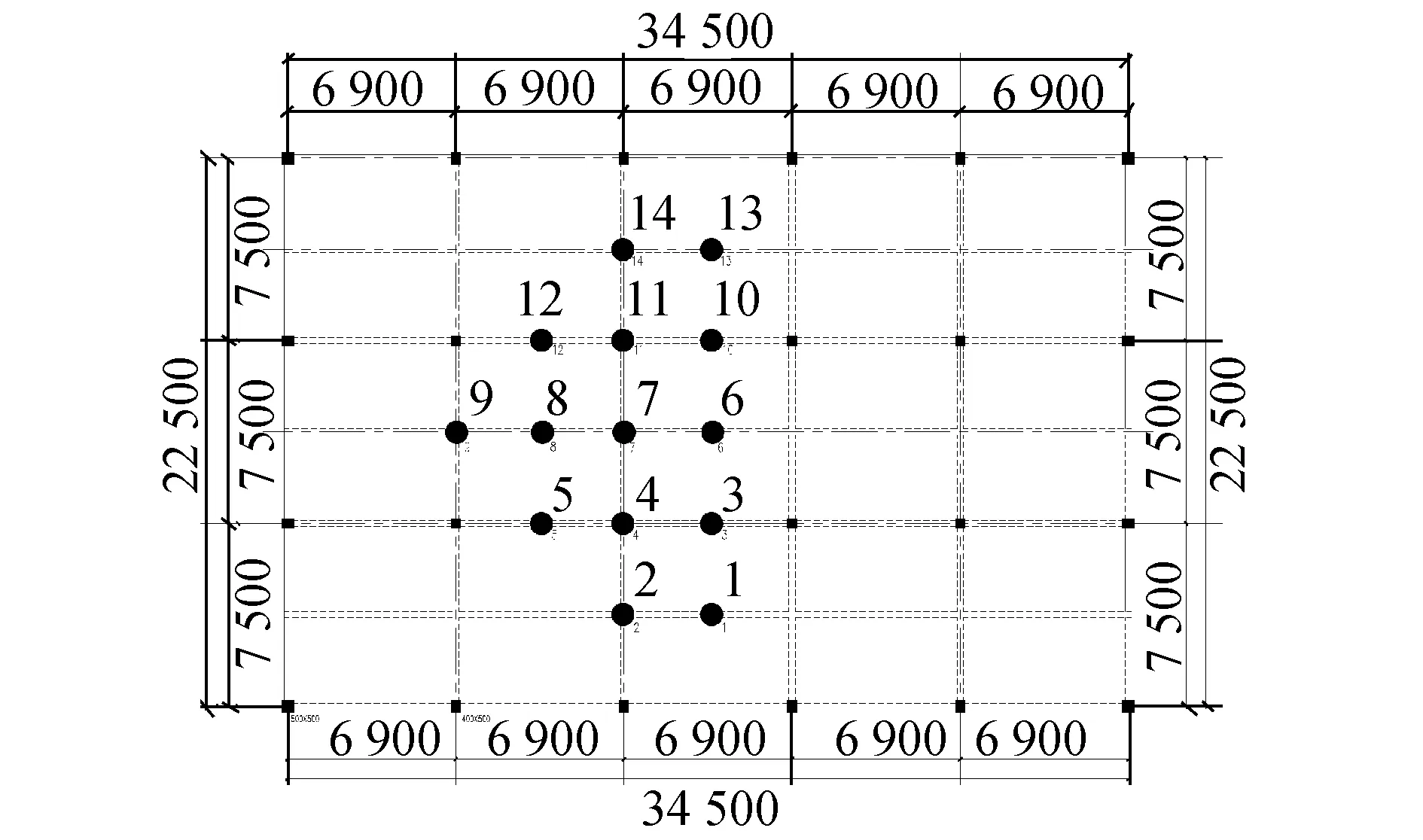
圖2 測點布置Fig.2 The plane layout of the test point
本次實測用到的儀器設備主要有:16通道東華(DHDAS-5921)動態信號采集分析系統1臺、100 m的2×0.3RVVP信號屏蔽線、東華2D001VDH610V速度傳感器及信號接收軟件等。其中,速度傳感器靈敏度指標在(0.33~0.37 V/(m·s-2)),可以滿足對樓蓋結構測試信號要求。
每組測試時間為25 min,數據采集頻率為0~100 Hz,采集完成后通過數據采集器對數據進行初步分析整理,分析不同激勵狀態下樓蓋的響應情況,從而得到樓蓋在不同時刻的速度變化情況。
2 有限元分析及約束條件
2.1 瞬態動力學理論
瞬態計算采用瞬態動力學平衡方程,將離散的有限元模型進行數值計算,得到不同時刻下的動力學響應,基本計算方程為:
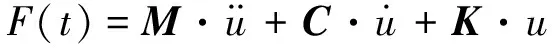
(1)
式中:F(t)為外加激勵作用;M為質量矩陣;C為阻尼矩陣;K為剛度矩陣;u為位移變量。
瞬態求解過程需要進行差分計算,其中最常用的方法為Newmark有限差分方法,在一個時間間隔內有:
(2)
(3)
式中:u為位移變化量;α、β為Newmark積分參數。
需要對下一時刻的位移un+1進行求解,對式(2)、(3)進行整理得:
(4)
(5)
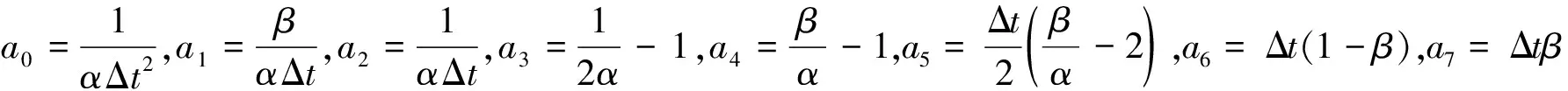
將方程(4)、(5)與方程(1)聯立可以求解出隨時間變化的瞬態動力學響應參數。
外加激勵F(t)則根據實驗速度激勵信號,通過傅里葉級數方法進行擬合,傅里葉級數的基本公式為:
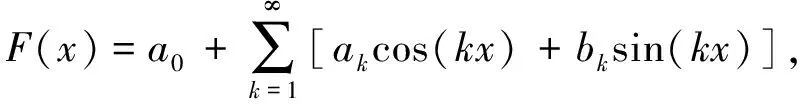
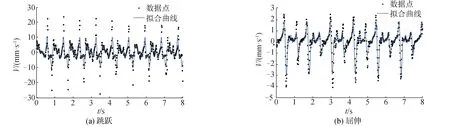
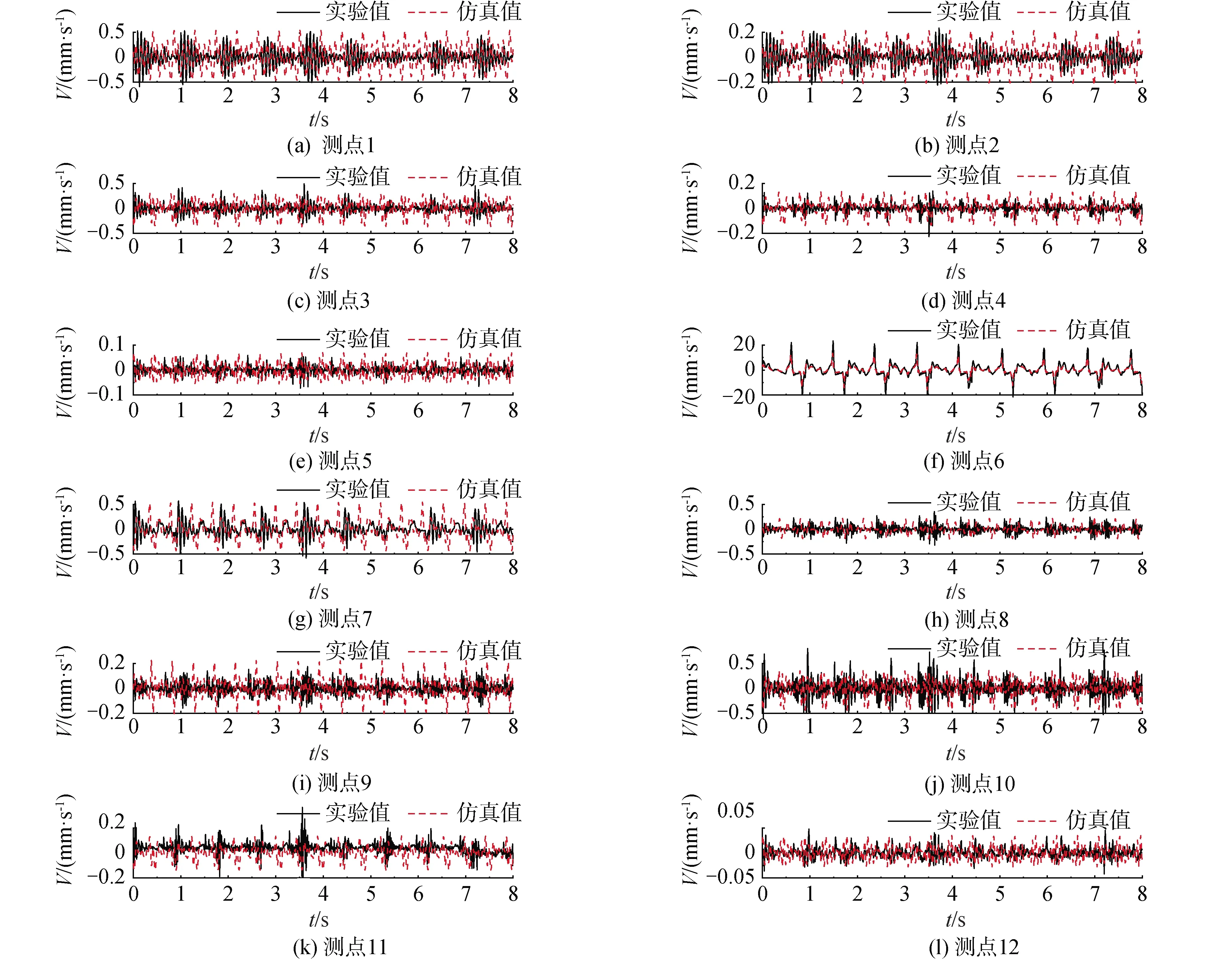
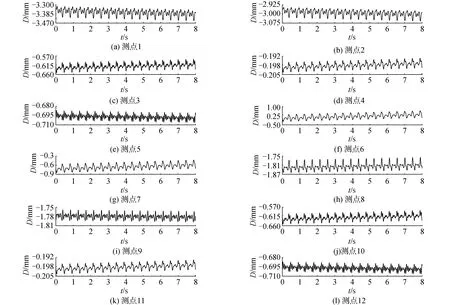
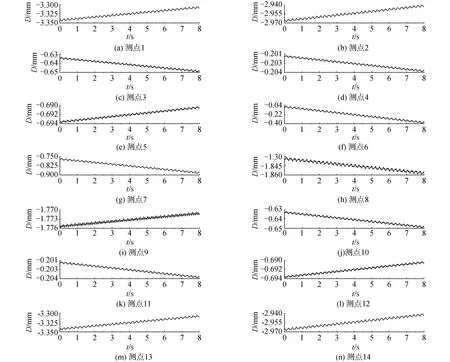
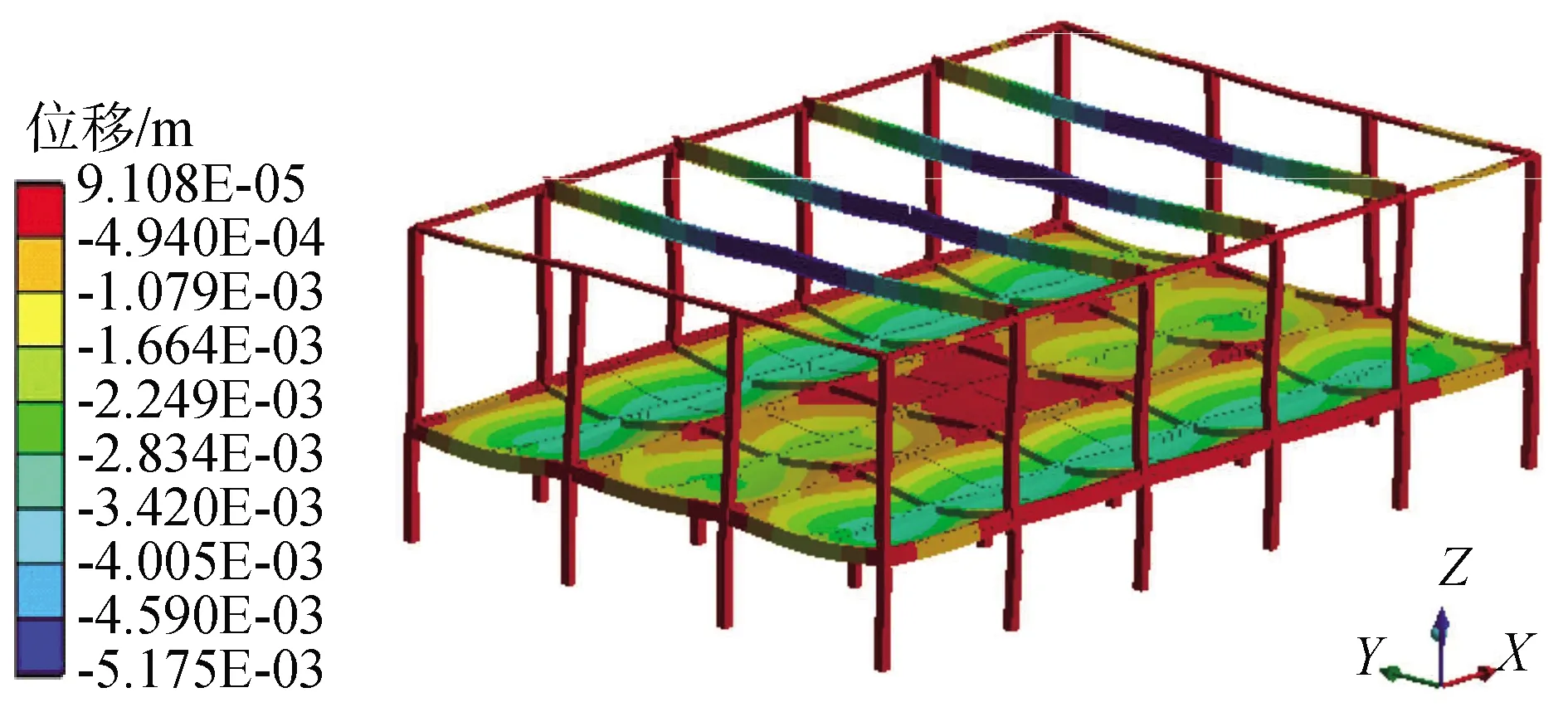
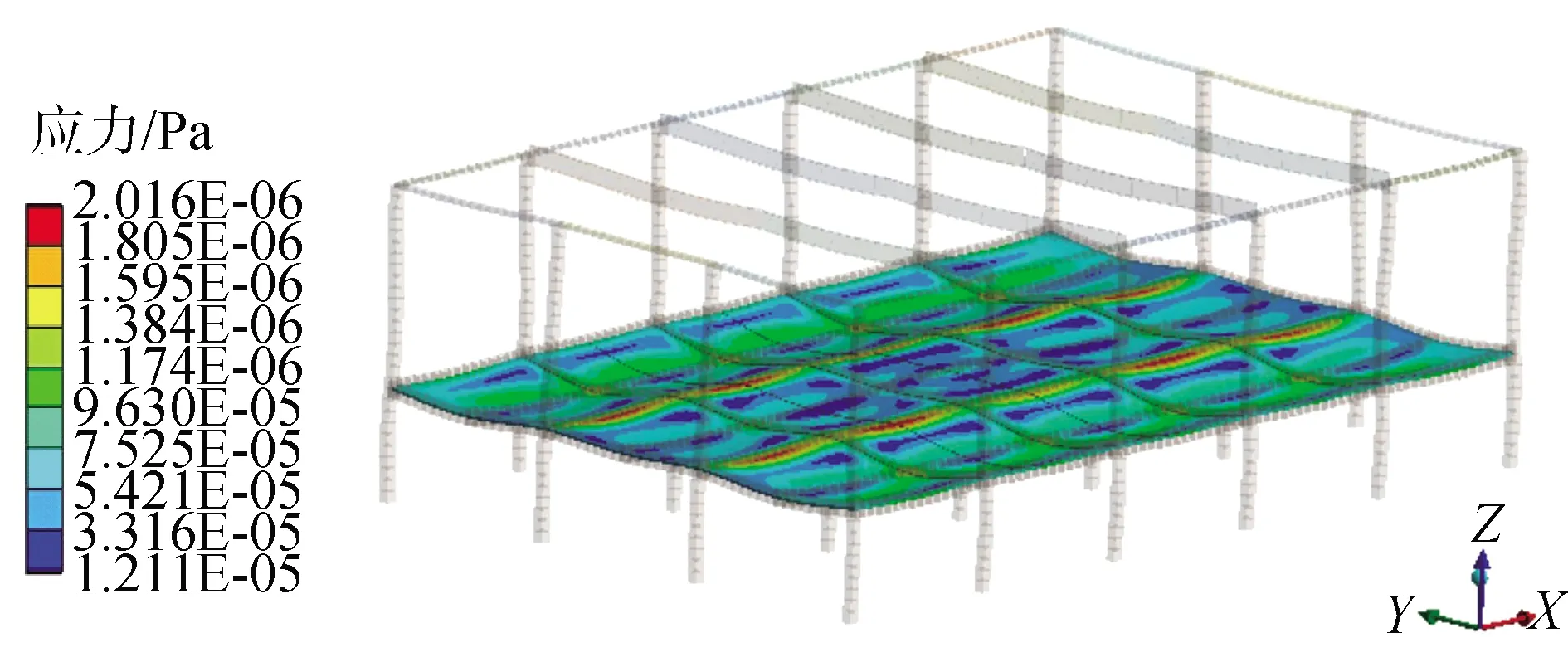
-π (6) 傅里葉級數可以對周期性函數進行準確的描述,展開的項數越多,擬合結果越精確,本文采用了8項展開式分別對跳躍和屈伸激勵實驗數據進行擬合,得到速度激勵函數: f(t)=a0+a1cos(wt)+b1sin(wt)+a2cos(2wt)+ b2sin(2wt)+a3cos(3wt)+b3sin(3wt)+ a4cos(4wt)+b4sin(4wt)+a5cos(5wt)+ b5sin(5wt)+a6cos(6wt)+b6sin(6wt)+ a7cos(7wt)+b7sin(7wt)+a8cos(8wt)+b8sin(8wt) (7) 經數值擬合,跳躍激勵時,ω為13.4;屈伸激勵時,ω為6.78,傅里葉級數多項式的系數如表1。2種激勵函數通過數據擬合得到的激勵曲線如圖3所示。 表1 2種激勵下傅里葉擬合系數 圖3 2種激勵速度擬合曲線Fig.3 Velocity fitting curves of two excitation 將速度激勵函數施加到數值仿真過程中,結合有限元方法對樓蓋進行瞬態動力學響應分析,并與試驗結果進行對照,驗證速度激勵函數作用下有限元模型分析過程中所引入的一系列理論參數是否符合實際情況,結構的動力響應是否符合實際要求,并進一步分析動力學響應的規律。 為了精確分析樓蓋的瞬態振動響應,本次采用樓蓋整體建模的方式,比較全面地考慮了樓蓋結構在整個建筑結構中的實際約束,利用ANSYS軟件建立三維有限元模型進行瞬態動力學分析,采用2節點BEAM188單元模擬梁單元,4節點SHELL181單元模擬板單元,采用自適應網格劃分六面體單元,有限元模型見圖4。 圖4 ANSYS 模型Fig.4 The model of ANSYS 為了精確模擬結構的動力響應特性,取混凝土密度為2 500 kg/m3,彈性模量為3.0×1010Pa,泊松比為0.2,混凝土板的阻尼取為0.05,本次有限元動力學分析采用瞬態動力學分析方法。 為了全面分析模型的動力學特性,約束條件保證支撐柱體結構與地面相連的部分為固定約束,梁、柱、板之間為固定約束,瞬態動力學分析時,計算方法采用完全法分析,該法適用于大型有限元模型瞬態動力學分析,并且可以允許各種類型的非線性現象,準確分析瞬態動力學結果。 通過單人激勵作用,分析了在不同激勵形式下樓蓋的響應規律及樓蓋的響應機理,總結了樓蓋的能量傳遞規律和響應形式。 實驗過程中采用的單人激勵形式包括跳躍運動和屈伸運動,激勵點位于6號測點位置;仿真過程通過實驗擬合出來的跳躍和屈伸2種形式的激勵函數,作用到6號測點位置,對比分析樓蓋結構14個測點位置的速度響應,分析在跳躍和屈伸運動2種激勵形式下各測點的動力學響應特性和能量傳遞分布規律。 把6號測點作為單人運動激勵點,激勵方式為跳躍運動時,得到實驗和有限元14個測點的速度響應信號如圖5所示,對比分析實驗測試和有限元結構測點的信號可以看出,各個測點速度響應表現出相同的規律,即6號激勵點速度幅值最大,此處為能量輸入位置;其次,在1、3、7、8、10、13號測點響應速度幅值在0.5 mm/s左右,2、4、9、11、14號測點響應速度幅值在0.2 mm/s左右,5、12號測點響應速度幅值分別在0.1 mm/s和0.05 mm/s。速度響應信號的大小反映了能量傳輸路徑上能量的分布情況。首先,作為激勵位置的6號測點,其響應為規則的跳躍運動信號,以此作為振動中心,能量首先傳到其相鄰的3、7、10號測點,而7號測點響應信號稍微小于3、10號測點,這是由于6號到7號測點之間存在橫梁,增加了質量阻尼,傳遞能量下降;其次,在次相鄰的1、8、13號測點速度幅值相對于相鄰測點有所減小,同時由于橫梁的阻尼作用,8號測點的速度幅值相對于其他2個測點有所減小;再次,隨著測點位置遠離激勵點位置,傳遞到2、4、9、11、14號測點能量繼續降低,最大速度減小到0.2 mm/s左右;最后,位于5、12號測點位置的響應速度最小,這是由于能量在傳遞過程中經過了立柱橫梁的阻隔,消耗了大部分的能量。 圖5 6號測點跳躍激勵時14個測點速度響應Fig.5 The speed response of 14 points under the jump excitation of No.6 point 能量的傳遞是以激勵點作為中心向四周傳遞到各個測點,但是能量的傳遞受到路徑的影響。從整體上看,2種方法得到的各個測點表現出相同的能量分布和傳遞形式,但有限元分析是一種理想模型分析,得到的結果更加規律,而實驗分析的數據則受到各種因素的影響往往出現數據分布的不均勻現象。 將6號測點的單人激勵變為屈伸運動,采集實驗和有限元14個測點的速度響應信號如圖6所示,2種方法測點響應表現出類似的規律:即作為激勵點的6號點,其響應速度幅值最大,1、3、7、8、10、13號測點響應速度幅值在0.05 mm/s左右,2、4、9、11、14號測點響應速度幅值在0.02 mm/s左右,5、12號測點響應速度基本小于0.02 mm/s。與跳躍激勵時的能量傳遞方式類似。首先,作為激勵位置的6號點,其振動為典型的屈伸運動信號,以此作為激勵中心,能量傳到其相鄰的3、7、10號測點,而7號測點由于橫梁增加了結構的阻尼,能量傳遞率下降,響應信號稍微小于3、10號測點;其次,在次相鄰的1、8、13號測點速度幅值相對于相鄰測點有所減小,同樣由于傳播路徑上橫梁吸能作用,8號測點的速度幅值相對于其他2個測點有所減小;再次,隨著測點位置遠離激勵點位置,傳遞到2、4、9、11、14號測點的能量繼續降低,幅值減小到0.02 mm/s左右;最后,距離激勵中心最遠的5、12號測點的響應速度最小。 圖6 6號測點屈伸激勵時14個測點速度響應Fig.6 The speed response of 14 points under the bounce excitation of No.6 point 在屈伸激勵過程中,能量的傳遞總體上以激勵點為中心向四周進行輻射,能量經過不同的路徑傳遞后,響應速度會以振動中心為基準,能量的傳遞會因為路徑上的梁柱作用出現局部減小的情況。有限元能量的傳遞需要通過各個單元節點進行數據傳遞,能量的傳遞規律是以激勵點作為能量中心通過單元節點向四周傳遞,這與實驗響應信號保持很好的一致性。在屈伸運動激勵的實驗測試中,其輸入的能量受到周圍結構的影響較大,因此響應信號規律性不強,有限元方法則表現為規律性較強的波動。 對比跳躍和屈伸運動作為激勵的樓蓋響應,可以看出,樓蓋結構的14個測點變化規律基本一致,尤其是在有限元方法中,規律更加明顯。這是由于對于同一研究對象,在2種運動激勵下,樓蓋的能量傳遞方式基本相同;然而,屈伸運動的響應速度幅值是跳躍運動響應速度幅值的1/10,這是由輸入的能量大小決定的;跳躍運動激勵下,所有測點的響應速度表現為拍振的響應,而屈伸運動激勵下,由于振動能量在傳播過程中對樓蓋阻尼敏感,所有點的速度響應則表現為隨機響應狀態。 為了進一步對照2種方法的一致性,全面系統的分析樓蓋結構整體動力學特性,分別對比試驗和有限元計算,在2種激勵形式下,不同時刻樓蓋整體結構的速度響應云圖如圖7、8所示,分析2種激勵形式下,樓蓋系統的動力學響應規律。 圖7 跳躍激勵下樓蓋速度響應Fig.7 Velocity response of floor under jump excitation 圖8 屈伸激勵下樓蓋整體速度響應Fig.8 Velocity response of floor under bounce excitation 提取不同時刻下樓蓋整體結構的典型速度響應云圖,對比每個時刻下對應的各個點,在試驗和有限元仿真的響應云圖,可以看出,在2種激勵下各自的響應幅值和振型,在對應區域的各個時間點的結果基本一致,有限元分析能夠準確反映樓蓋結構的振動形式和能量變化規律。 進一步對比4個不同時刻,在跳躍和屈伸運動激勵下的速度響應情況可以看出,對于樓蓋結構的速度激勵,由于其具有周期性激勵的形式,使得樓蓋結構的速度響應以激勵點為中心,向四周呈復合正弦波形傳播,其波動隨著時間呈周期性變化,整體結構隨著時間的速度的峰值也呈周期性變化;對比跳躍和屈伸激勵狀態的速度響應可以看出,跳躍激勵的速度響應值與屈伸激勵響應值相差一個數量級,并且跳躍傳播的能量波動范圍大于屈伸激勵能量范圍,整體結構速度的響應更加連續具體的反映了樓蓋結構在2種激勵下的能量傳遞規律和振動規律。 位移的變化是反映樓蓋結構在受到載荷作用下,樓蓋保持穩定性的一個重要方面,通過有限元方法可以對各種激勵作用下的樓蓋位移變化進行分析,對樓蓋結構的穩定性提供參考。 在跳躍激勵作用下,樓蓋結構各個監測點表現為周期性振動變化趨勢(圖9)。 圖9 跳躍激勵位移響應曲線Fig.9 Displacement response curves of jump excitation 同時各個測點從整體上看,有向不同的方向運動的趨勢,由于跳躍激勵能量比較大,位移響應主要以周期性振動形式變化,在重力和跳躍激勵函數的共同作用下,使得位于不同位置測點上的位移,表現出不同的運動趨勢,1、2、13、14號測點位移最大,這是由于測點在外側橫梁位置,跳躍激勵的能量受到相鄰立柱橫梁的阻隔作用,主要受到自身重力的作用,并且在自身重力作用,測點位置有向下運動趨勢;7、8、9測點與激勵點在一根橫梁位置,因此受到跳躍激勵的影響相對明顯,使得測點受到周期性激勵的影響,成復合正弦波形變化;3、4、5、10、11、12測點位移較小,由于在4、11測點位于立柱支撐位置,限制了2點的運動,使得此處的測點位移最小。立柱位置和靠近激勵點位置的測點位移向上微小運動,遠離的測點向下運動,呈復合正弦波形變化。 在屈伸激勵作用下,各個測點總體上與跳躍激勵效果一致,有向不同的方向變化的趨勢(圖10),然而由于激勵載荷較小,使得每個測點的周期性波動微小,在重力和屈伸激勵的共同作用下,使得各個測點的位移表現出不同的規律。1、2、13、14號測點位移最大,這是由于在外側位置主要受到自身重力作用,測點位移主要向重力方向變化;7、8、9測點受到屈伸激勵的影響相對明顯,使得測點受到振動激勵的影響呈復合正弦波形變化;3、4、5、10、11、12測點位移較小,主要由于在4、11測點受到立柱的支撐作用,限制了其位移變化。立柱位置和靠近激勵點位置的測點位移向下微小運動,遠離的測點向上運動,呈復合正弦波形變化。 圖10 屈伸激勵位移響應曲線Fig.10 Displacement response curves of bounce excitation 對比在2種激勵下樓蓋局部測點的響應規律可以看出,相對于屈伸運動激勵的變化,跳躍運動輸入較多的能量,測點位移幅值表現出明顯的周期性運動,而屈伸激勵作用時,其位移幅值變化較小;從位移響應整體變化規律來看,2種激勵形式的最終振動平衡位移相近,位移的變化是在重力作用的基礎上產生的周期性變化。跳躍激勵的振動幅值是屈伸激勵振動幅值的10倍,跳躍激勵對系統具有更直接的影響作用。在激勵過程中,由于樓蓋結構自身的特點,使得2種激勵形式下的位移響應變化都出現周期性復合正弦波形傳播。但傳播過程中受到立柱橫梁的影響,能量傳播受到限制,在中間位置靠近激勵點的測點受到激勵運動的影響明顯。 對樓蓋整體結構有限元模型位移結果進行進一步分析可以看出,整體位移的變化反映了樓蓋的變形規律。從位移變形規律來看(圖11、12),跳躍、屈伸運動激勵使樓蓋結構在激勵點附近出現向上運動趨勢,位移出現最大值,從整體結構位移分布來看,2種激勵產生的位移分布規律基本一致,即在立柱支撐位置的位移,明顯高于無立柱支撐和梁頂位置。而由于跳躍激勵相對屈伸激勵具有更大的能量峰值,因此,對中間激勵位置產生更明顯的影響,跳躍激勵位移峰值明顯高于屈伸激勵位移峰值。 圖11 跳躍激勵下樓蓋整體位移響應Fig.11 Displacement response of floor under jump excitation 圖12 屈伸激勵下樓蓋整體位移響應Fig.12 Displacement response of floor under bounce excitation 為了進一步研究樓蓋結構在不同激勵下的安全性,從2種激勵下的樓蓋應力的響應進行分析(圖13、14),重力的作用和立柱的支撐影響,使得應力集中出現在立柱所在的2行橫梁位置,橫梁結構承受了最大的壓力,成為危險位置,同時由于2種激勵的擾動作用,使得激勵地點附近橫梁的應力集中值減小。跳躍激勵的能量輸入大于屈伸運動,使得激勵對橫梁的影響更加明顯,對整個樓蓋結構的振動位移產生較大的影響,對樓蓋產生較大的危害。 圖13 跳躍激勵下樓蓋整體應力響應Fig.13 Stress response of floor under jump excitation 圖14 屈伸激勵下樓蓋整體應力響應Fig.14 Stress response of floor under bounce excitation 1)通過單點拾振獲取所測樓板各測點的振動響應速度,通過傅里葉級數理論擬合得到了激勵位置的速度激勵函數,分析對比了2種激勵下樓蓋的實驗和數值響應結果,表明速度激勵函數結合有限元方法進行數值分析與實驗值對照較好,證明了理論計算的可行性。 2)單人單點激勵時,跳躍和屈伸作用到樓蓋的能量傳遞規律相同;跳躍運動激勵下,所有測點的響應速度表現為拍振響應,而屈伸運動激勵下,所有點的速度響應則表現為隨機響應狀態,這是由于輸入能量較低時,速度響應容易受到樓蓋結構的擾動而出現無規律運動狀態。 3)從振動位移角度,解釋了人致振動下樓蓋危險位置位于中間懸空位置,應采取有效的措施,加強中間位置的結構支承。 4)通過有限元方法分析可以看出,在2種激勵的周期性作用下,樓蓋結構會出現規律的復合正弦波運動形式,并使激勵位置出現向上的運動趨勢。
2.2 有限元模型

2.3 材料參數選取
3 人致振動激勵瞬態分析
3.1 各測點速度對比分析

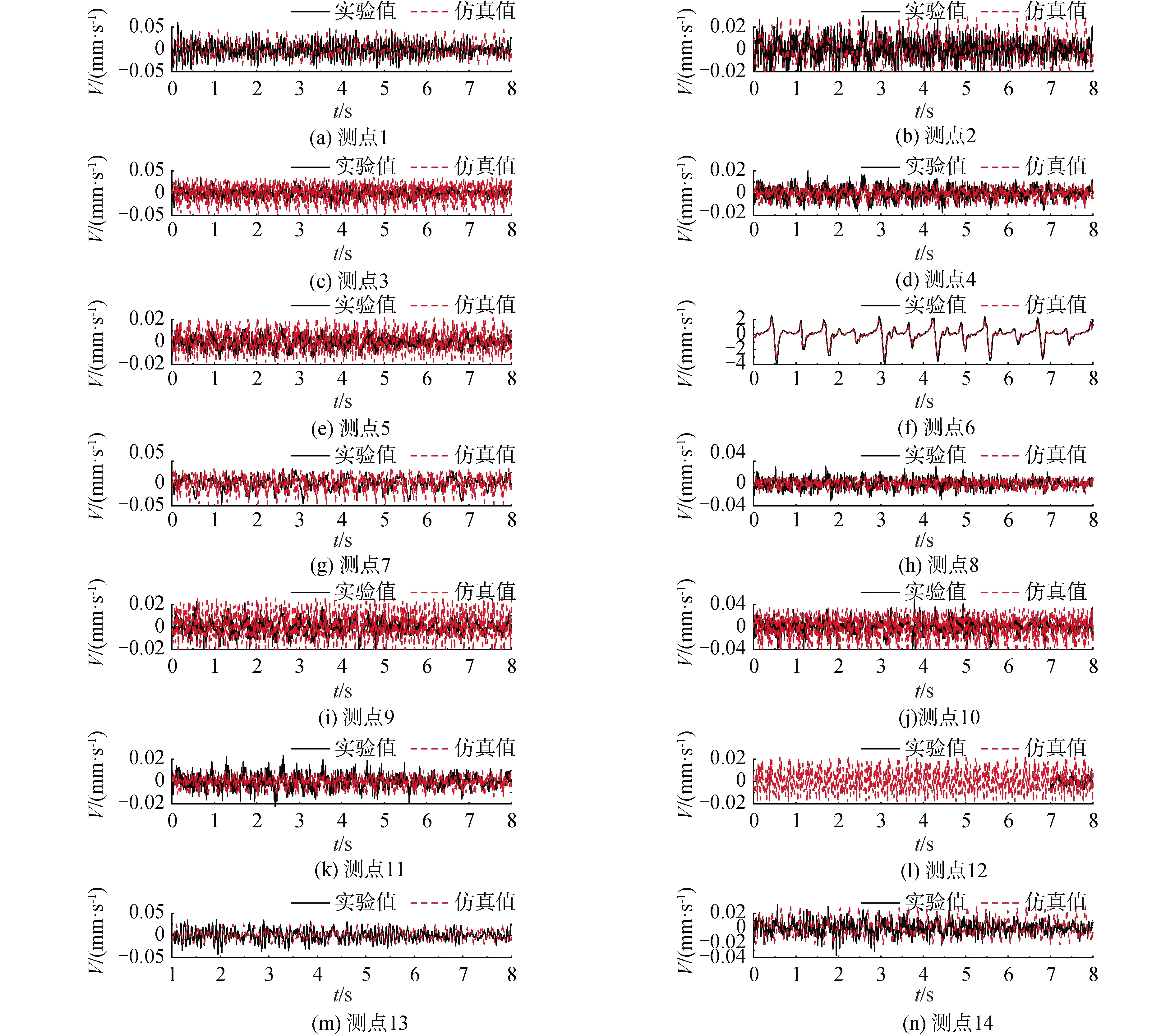
3.2 樓蓋整體速度響應對比分析
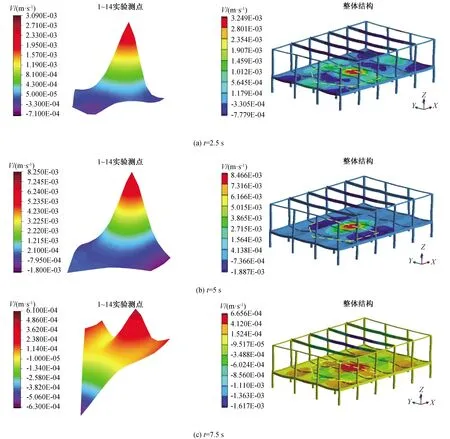
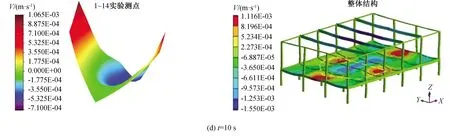
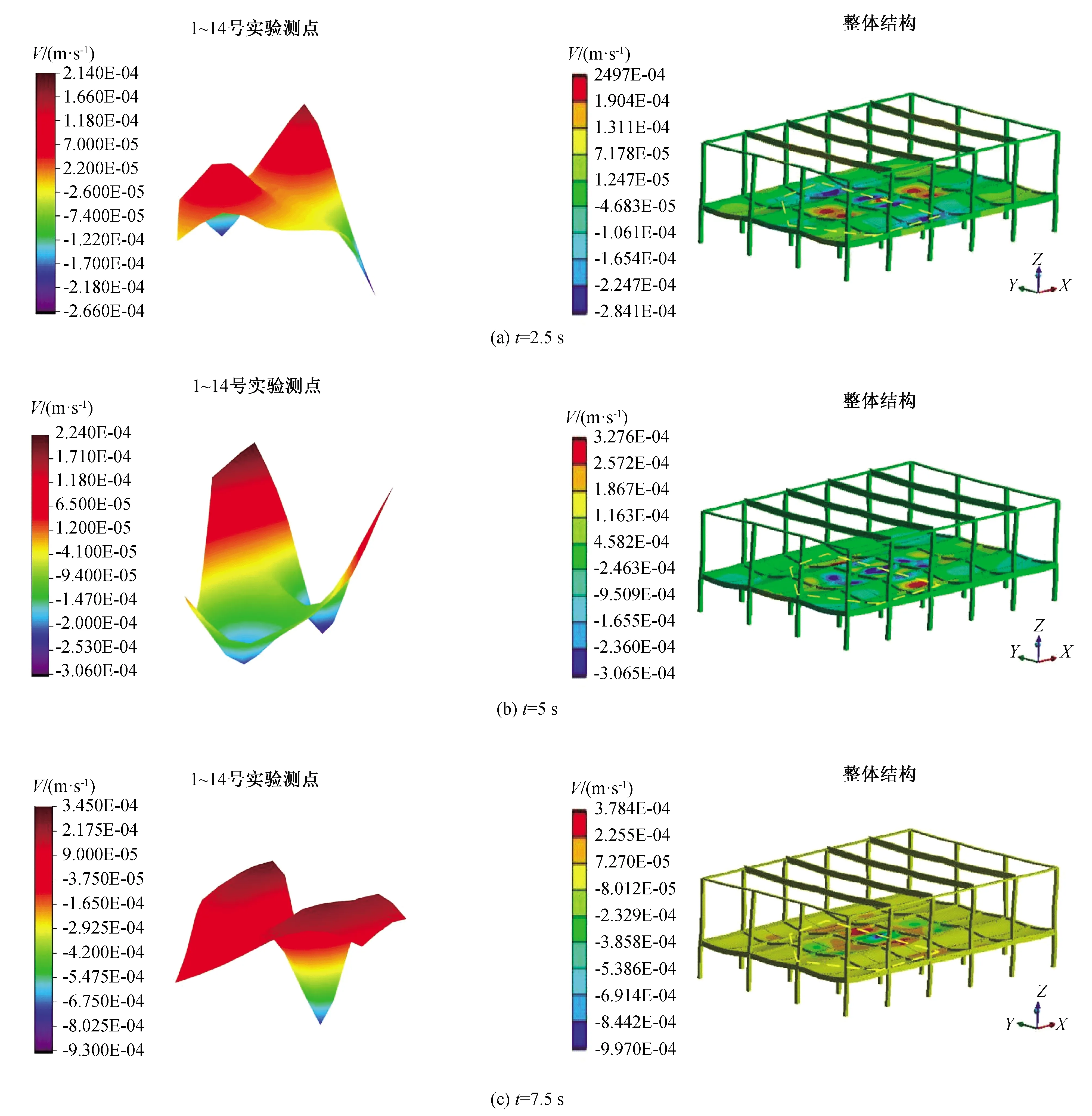
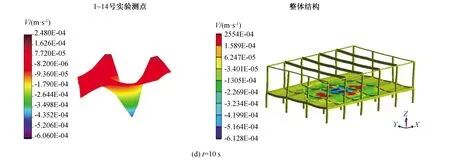
3.3 各測點和樓蓋整體位移響應及應力分析
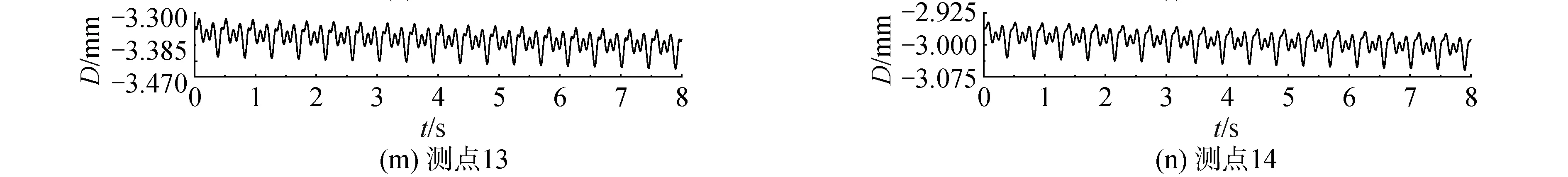


4 結論

