基于結構可置信性魯棒優化算法的離散優化問題研究

23232323

(1.大連大學 機械工程學院，大連 116622； 2.大連理工大學 工業裝備國家重點實驗室 工程力學系，大連 116024；3.大連理工大學 寧波研究院，寧波 315016)

1 引 言

結構優化設計按照設計變量類型可以分為連續變量優化設計和離散變量優化設計。而實際上，大多數工程設計對應于離散變量優化設計問題。因為許多工程構件的選擇都遵循一套標準化的計量辦法，以滿足工業化大生產的要求；同時測量工具通常也具有特定精度和量程，因而導致工程結構的參數通常是離散的。相對于連續優化的理論，離散優化理論的發展還處于遠不成熟的階段[1,2]。當前在處理實際工程的離散變量設計問題時，出現了兩種不同的思路。一種首先采用連續優化方法得到一組最優解，然后對解的每個分量采用四舍五入或者向上取整等方法得到離散解，并憑工程師的經驗對其進行適當調整和驗證，以滿足產品設計的需求。另一種做法是直接根據離散數學及其相關優化算法，基于嚴謹的理論分析和數值計算來求得工程設計問題的離散最優解。盡管現階段來說，后種做法的計算量較大且可解決的問題也相對有限，但此類基于理性的研究方法對完善結構優化體系和指導工程設計均具有重要意義。

根據研究問題的角度不同，離散優化設計的分類方法有多種，如隋允康等[3]把離散變量優化方法分為圓整方法、離散方法和離散優化映射為連續優化的方法。Arora等[4]對非線性離散變量優化問題相關工作進行了總結。陳立周[5]撰寫了國內關于結構離散優化方面較早的專著。柴山等[6]提出了精確的啟發式算法，即相對差商法，能夠解決目標函數和約束函數單調的離散優化問題。Templeman等[7]通過構造力學模型使離散變量問題映射為連續變量問題，予以求解后反演回離散變量問題的解。李興斯等[8]把離散變量結構優化設計問題轉化為帶有互補約束的優化問題，并利用NCP函數進行求解。譚濤[9]介紹了離散變量優化設計的連續化方法。石連拴等[10]提出了離散變量結構優化設計序列定界組合算法。王躍方等[11]研究了多工況下受應力和位移約束的離散截面變量桁架結構的布局優化問題。Juang等[12]采用修正的離散拉格朗日搜索法解決了桁架結構的離散優化問題。Wolkowicz等[13]采用半定規劃方法來求解離散優化問題和矩陣完成問題。此外，Bertsimas等[14]提出了魯棒離散優化(RDO)理論，利用整數規劃方法考慮了概率邊界，并主要用于求解網絡流問題。

另一方面，傳統優化設計的研究通常認為問題的參數(如材料屬性和外載荷等)是確定的，可以精確給出。但在實際應用中參數的不確定性是無法避免的，如產品制造或者測量時都可能引入系統誤差和人工誤差。更值得注意的是，某些優化問題可能對參數的波動具有非常高的靈敏度[15]。因而隨著計算技術的快速發展，考慮不確定性的結構優化設計近年來受到越來越多的關注，相關數值優化方法大量涌現。一般來說這些方法分為兩類，一類是基于概率模型，另一種則基于非概率模型。由于獲得不確定性參數的概率分布函數需要較大的樣本，并且研究發現概率模型對其自身的參數(如均值和方差等)較為敏感，采用非概率模型解決不確定性結構優化問題受到了廣泛關注。

在非概率框架下，不確定參數通常假定為未知但有界的集合，而無需具體的參數概率分布信息。魯棒優化的研究目標之一為在不確定框架下尋找一個最優解，使得不確定性參數在給定集合中取任何值都能滿足約束條件，也稱為最不利情況的設計和優化WCDO(Worst Case Design and Optimization)。非概率不確定性優化在數學規劃領域的研究開始于Ben-Tal等[16-18]以及El Ghaoui等[19,20]的開創性工作。隨著解決凸優化問題的內點法(特別是半定規劃)的快速發展[21]，已發展出大量的理論研究成果和技術工具用來求解凸優化問題的魯棒最優解。Ben-Tal等[22]系統地研究了魯棒優化中的線性規劃、錐規劃和半定規劃問題。Calafiore等[23]發展了計算不確定線性方程組的最小定界橢球法。作為不確定性分析的強大工具，區間代數通常用于WCDO問題的求解。Chen等[24]提出了區間優化方法用于不確定結構的分析，通過結合泰勒展開技術的區間擴充運算，導出了一個確定性問題的列式。近來，Guo等[25]應用區間分析中估算不確定性結構響應的界限，進而構造了魯棒設計列式。除了區間模型外，基于橢球凸模型的魯棒優化設計問題也受到了學者們的廣泛關注[26-29]。

綜上所述，離散優化問題和非概率不確定優化問題的研究方法存在較大差異。若把其割裂開來，如單純考慮結構不確定性，所得到的最優設計(如件的橫截面積)將很難找到相匹配的工業型材，而相近型材對應設計的可行性以及魯棒性難以有效保證。而若單純考慮結構設計變量的離散性，得到的最優設計的安全性和魯棒性又是未知的。本文研究發現若把結構魯棒優化的不確定參數看作未知且有界，則其求解方法和離散優化問題的求解方法則具有相似性；進而提出了基于結構可置信性魯棒優化算法的離散優化問題求解新思路，稱為魯棒圓整法，能夠解決同時考慮參數不確定性和離散性的結構離散魯棒優化問題，保證其最優解取離散值且在不確定性的情況下仍然能夠滿足約束條件，從而更好地應用于解決工程實際問題。

2 求解離散優化問題的魯棒圓整法

事實上，魯棒優化的基本思想和傳統連續優化圓整法之間存在著內在的聯系。首先如圖1所示，A,B,C和D四點都在連續最優解附近，都可能選為圓整后的離散最優解，但是其中最為接近連續最優解的點A卻是違反約束的不可行點(如桁架面積的連續最優解經過圓整以后引起了內力重分布，對位移函數和目標函數都有影響)，圓整解的可行性無法得到理論上的保證。由于工程實際問題會盡量避免可行性無法得到保證的最優設計，而通常允許設計值存在一定的安全裕度，因此有必要對傳統連續優化圓整法做出改進，使得經過圓整后的最優解能夠在理論上自然滿足約束條件。

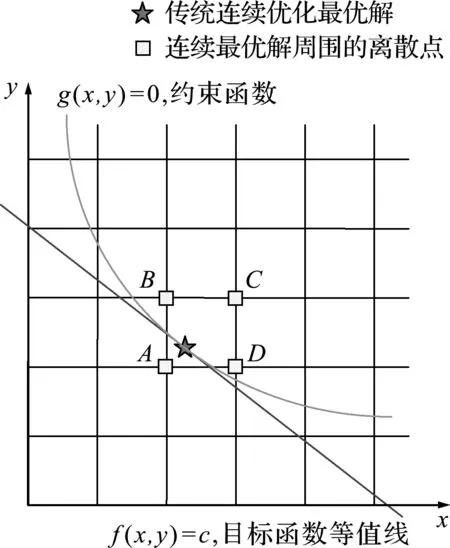
圖1 傳統連續優化圓整法

為了實現這一目標，可以首先在連續優化階段構造魯棒優化問題并采用可置信性魯棒優化方法得到最優解，然后對該解在其魯棒性允許的區間內進行圓整得到離散的最優解，本文把這樣的方法稱為魯棒圓整法。

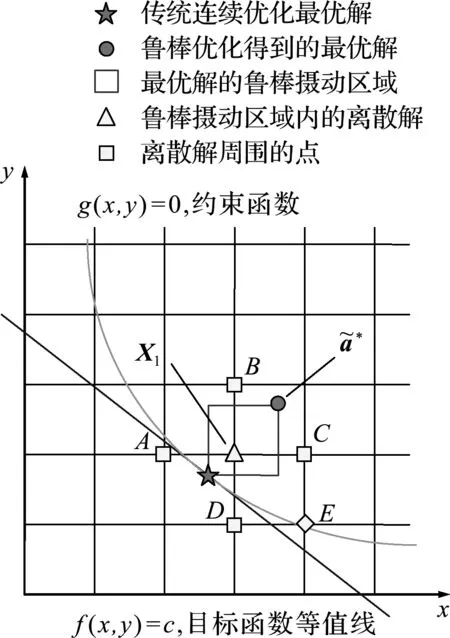
圖2 魯棒圓整法(一)

2.1 離散優化問題的等價魯棒優化列式

魯棒圓整法的目的和傳統的連續優化圓整法一樣，都是要求解離散優化問題。本文以桁架結構重量極小化問題為例，確定性離散優化問題的整數規劃列式如下，

(1)

現在構造以下魯棒優化問題，

(2)

2.2 魯棒優化列式的求解

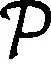
(3)

(4)

不確定區間是非對稱的，需要進行轉換，由于

(-1≤ξi≤1)

令

(5)

(6)

式中ξ=(pT,1)T∈Rnm +1

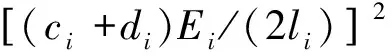
(7)

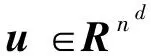
(8)

等價于

(9)

(10)

(11)

其他的結構響應約束(如應力)可以采用完全類似的方法來處理。

(12)

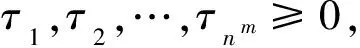
(13)

基于以上分析和討論，原優化問題轉化為如下可置信性的單層優化列式,

τi≥0 (i=1,…,nm)

(14)

2.3 離散可行解的修正

為求解離散優化問題，2.2節通過可置信性魯棒優化以及魯棒圓整找到了一個能夠自然滿足約束條件的離散可行解X1，X1是魯棒性區域內唯一的離散點，本文對其最優性進行討論。

首先對一階離散局部最優解進行定義，從魯棒圓整得到的離散可行解X1出發，每次只改變一個分量，移動到相鄰的離散點處，如圖2和圖3所示，二維問題共有4個相鄰點，分別是A,B,C和D四點，如果不存在滿足約束且比X1處目標函數更小的離散解，那么就稱X1為一階離散局部最優解。

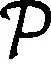
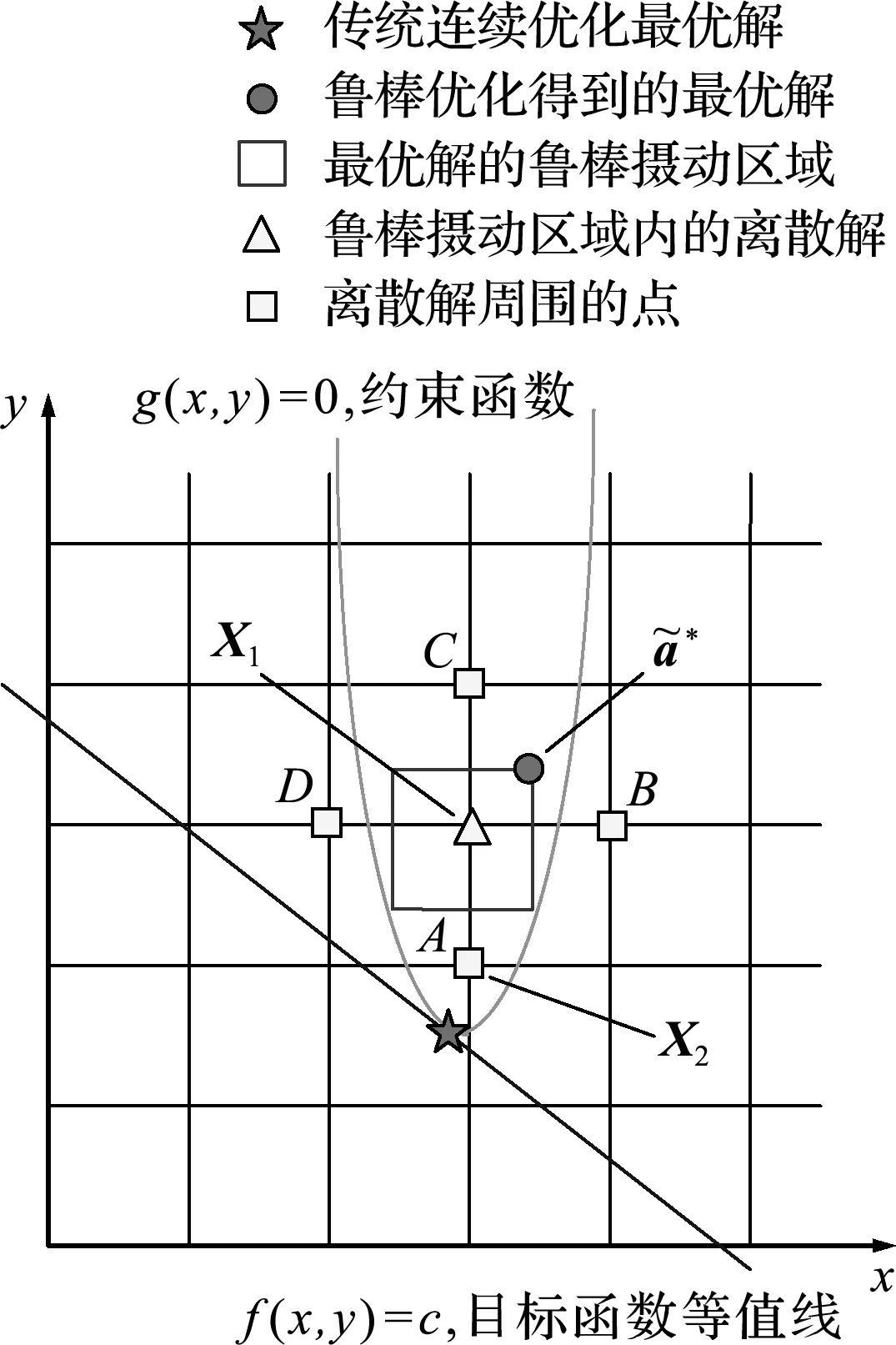
圖3 魯棒圓整法(二)

本文利用相對靈敏度商的規則或者相對差商規則[6]對X1進行修正，步驟如下。

(1) 首先在橫截面積沒有達到下限的桿件中，根據規則找到第j號桿件的橫截面積aj，使其下降到相鄰的整數，即第j號桿件的橫截面積aj更新為aj-1。

(2) 檢查約束條件是否滿足，如果滿足，跳回步驟(1)繼續執行；否則把aj賦回原值，即把aj+1賦值給aj，得到一階離散局部最優解，記為X2。

(3) 對X2繼續修正，減少一個目標函數靈敏度大的桿件面積，同時增加一個目標函數靈敏度小的桿件面積，如果滿足約束，那么得到更好的局部最優解X3；否則采用步驟(2)得到的局部離散最優解X2。

由于步驟(2)所得的最優解X2已經達到了一階局部最優性，步驟(3)將得到滿足更高階精度的局部最優解，如圖2的點E。一般來說一階離散局部最優解能夠滿足實際需要，為了節省計算量，在本文算例中只追求一階離散局部最優解X2。

現對上述改進方法的步驟(1)需要滿足的規則進行詳細闡述，本文有兩種下降規則，第一種是需要提供當前點的解析靈敏度，稱為相對靈敏度商規則；第二種是需要計算相鄰兩步之間的差分值，稱為相對差商規則。采用兩種規則所得到的最優解一般是不同的(但通常很接近)，本文可以選取其中較好的一組作為離散最優解。

首先介紹相對靈敏度商規則。假設第i號桿件的面積ai發生改變，目標函數的靈敏度可以寫為

?W/?ai=ρili

(15)

約束函數的靈敏度可以寫為

(16)

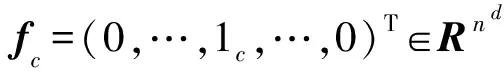
(1) 在全部nm根桿件中，如果存在第j號桿件，使得約束函數的靈敏度?g/?aj≥0，那么選取第j號桿件的面積aj變為aj-1。事實上X1的分量中，滿足這樣條件的aj很可能已經達到下限。若不存在則轉向下一步。

(2) 全部nm根桿件中，?g/?ai<0 (i=1,…,nm)，本文知道選取使目標函數下降較快，而約束函數上升較慢的桿件來調整比較有利，所以定義參數

(17)

找出其中的最大值βj≥βi(i=1,…,nm)，對應的桿件j，面積aj變為aj-1。

相對差商規則和相對靈敏度商規則比較類似，假設第i號桿件的面積ai發生改變，目標函數的差分方程可以寫為

(18)

約束函數的差分方程可以寫為

(19)

(1) 在全部nm根桿件中，如果存在第j號桿件，使得約束函數的差分敏度Δg/Δaj≥0，那么選取第j號桿件的面積aj變為aj-1。事實上X1的分量中，滿足這樣條件的aj很可能已經達到下限。若不存在則轉向下一步。

(2) 全部nm根桿件中，Δg/Δai<0(i=1,…,nm)，由于選取使目標函數下降較快而約束函數上升較慢的桿件來調整比較有利，所以定義參數

(20)

找出其中最大值βj≥βi(i=1,…,nm)，對應的桿件j，面積aj變為aj-1。

值得注意的是相對靈敏度商規則的使用有一個前提，即當前點和將要移動到的點兩者的約束靈敏度符號必須一致，郭旭等[30]已經證明了在桁架結構中存在這種單調性特征，所以使用相對靈敏度商規則也是有理論依據的。

2.4 魯棒圓整法求解離散優化問題的流程

本文給出了離散優化問題的魯棒圓整法流程，如圖4所示。

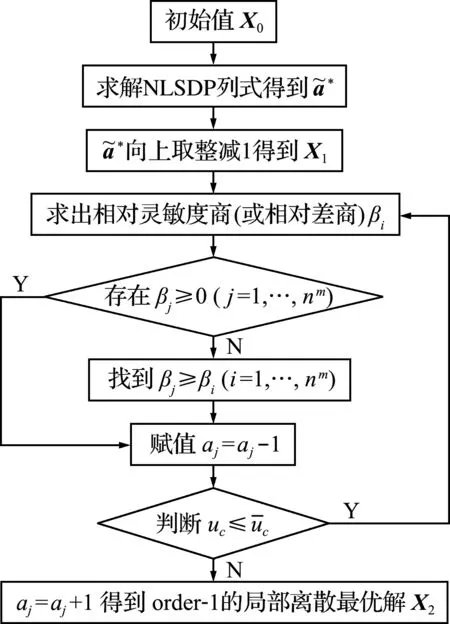
圖4 魯棒圓整法流程

2.5 魯棒圓整法求解離散優化問題的數值算例

本節通過2個桁架結構重量極小化問題說明魯棒圓整法的有效性。所有桿件的彈性模量是 100 GPa，密度為10 g/cm3，橫截面積初始值為1 cm2。

算例129桿桁架結構

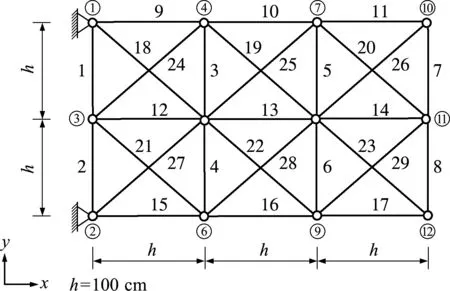
圖5 29桿桁架

圖6 29桿離散結構優化問題目標函數的魯棒圓整法迭代曲線

算例251桿桁架結構

如圖7所示的51桿桁架結構，所有桿件的橫截面積只能在[3,100]取整數值。外載荷向量f=(10,0)TkN作用在3,5,7,9,11號節點上。約束為13號桿件的水平方向位移u13x不大于1 cm。表2列出了魯棒圓整法和傳統連續優化圓整法所得的最優橫截面積及結構重量等的比較。由表2可知，魯棒圓整得到的離散解X1滿足約束條件，一階離散局部最優解X2非常接近于連續優化的最優解，而傳統連續優化圓整(四舍五入)后并不滿足約束條件。

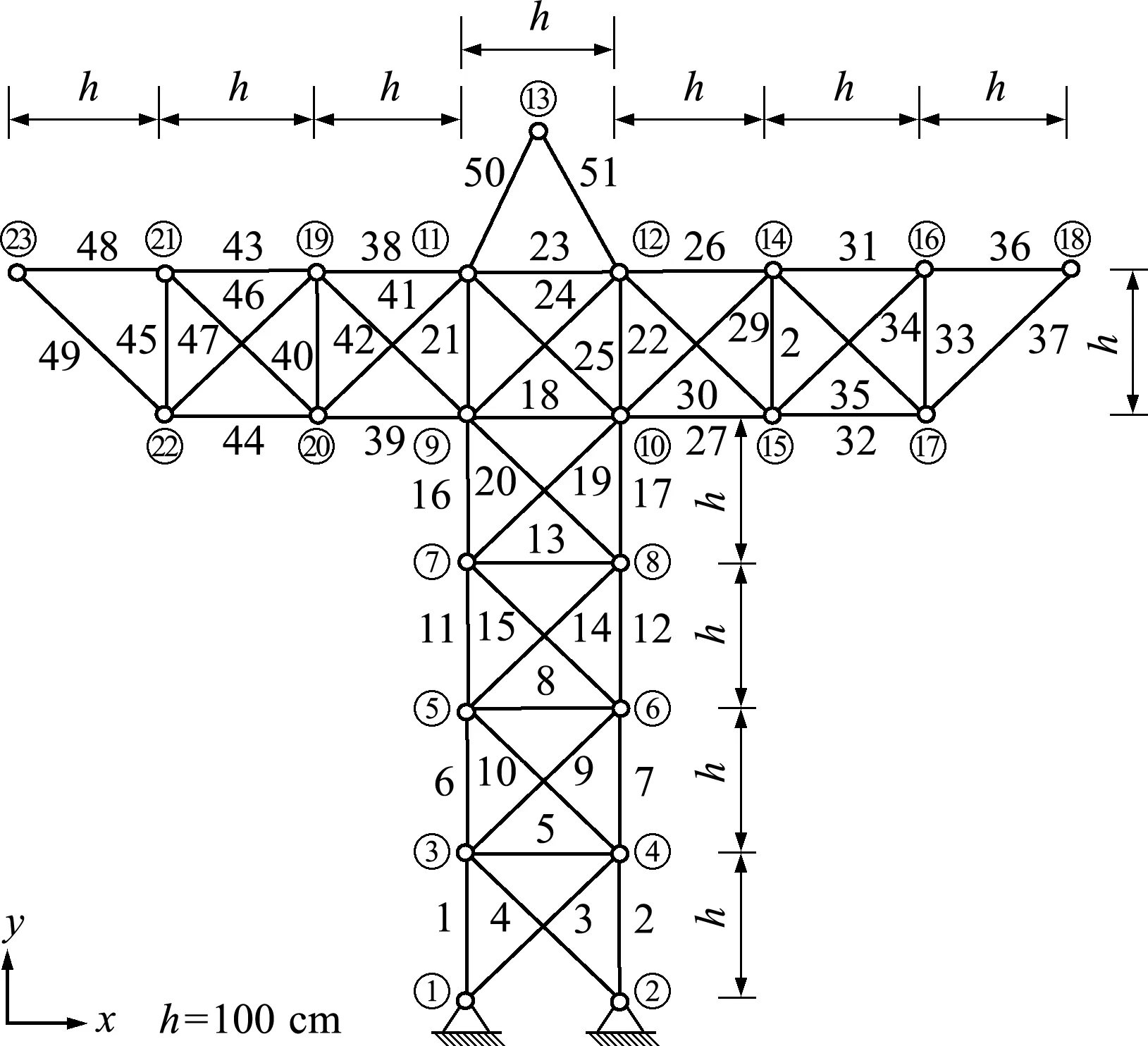
圖7 51桿桁架結構

表2 魯棒圓整法和傳統連續優化圓整法最優解的比較(單位：cm2)

3 魯棒圓整法求解剛度不確定的

離散魯棒優化問題

剛度不確定的魯棒優化問題可以使用單層的NLSDP方法[25]求解，但所得到的最優桿件橫截面積仍然在正數范圍內取連續值，而實際桿件橫截面積的取值通常是一個離散數的集合。這就需要把考慮參數的不確定性和設計變量的離散性相結合，發展求解魯棒問題可置信性離散最優解的方法。本文分兩個小節分別介紹使用魯棒圓整法求解離散魯棒優化問題的數學模型和離散可行解的修正方法，最后通過數值算例證明方法的可靠性。

3.1 離散魯棒優化問題的模型和求解

以剛度不確定的桁架結構重量極小化問題為例，假設橫截面積為正整數，本文首先給出離散魯棒優化的數學規劃列式，

(21)

本文考慮兩種剛度不確定性刻畫方法,

(22)

魯棒圓整法需要求解的魯棒優化問題就是采用這種不確定性模型。

(23)

(24)

(25)

3.2 離散魯棒優化問題離散魯棒可行解的修正

如2.3節所述，本文可以利用相對靈敏度商的規則對離散魯棒可行解X1進行修正，步驟如下。

(1) 首先在橫截面積未達到下限的桿件中，根據規則將第j號桿件的橫截面積aj更新為aj-1。

(2) 檢查約束條件是否滿足。如果滿足，跳回步驟(1)繼續執行；否則把aj賦回原值，即把aj+1賦值給aj，得到滿足魯棒性約束條件的一階離散局部最優解X2。

與離散優化問題的區別是，離散魯棒優化問題每次判斷最優解是否滿足約束時，都要進行魯棒問題的結構極值響應分析，本文可以采用郭旭等[30]提出的精確結構極值響應方法，或者基于靈敏度定界的結構極值響應方法[31]求得位移極值，這樣就可以檢查每一步設計變量改變后能否滿足約束條件。

但不確定問題的精確位移極值響應的求解過程比確定性問題位移的求解要復雜很多，計算量很大。若在中間過程使用快速的近似算法替代，直到繼續改進離散解會違反約束時，再采用精確的結構位移極值響應分析方法進行嚴格檢驗，則可避免在迭代中頻繁使用全局最優化算法，從而提高整體計算效率。

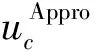
(26)

除了較為精確，單調性方法的另一個好處是在每一步迭代中幾乎不增加任何計算量，因為在采用相對靈敏度商規則判斷下降方向的時候，已經進行過靈敏度分析。

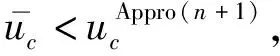
圖8 離散魯棒優化問題收斂過程(一)

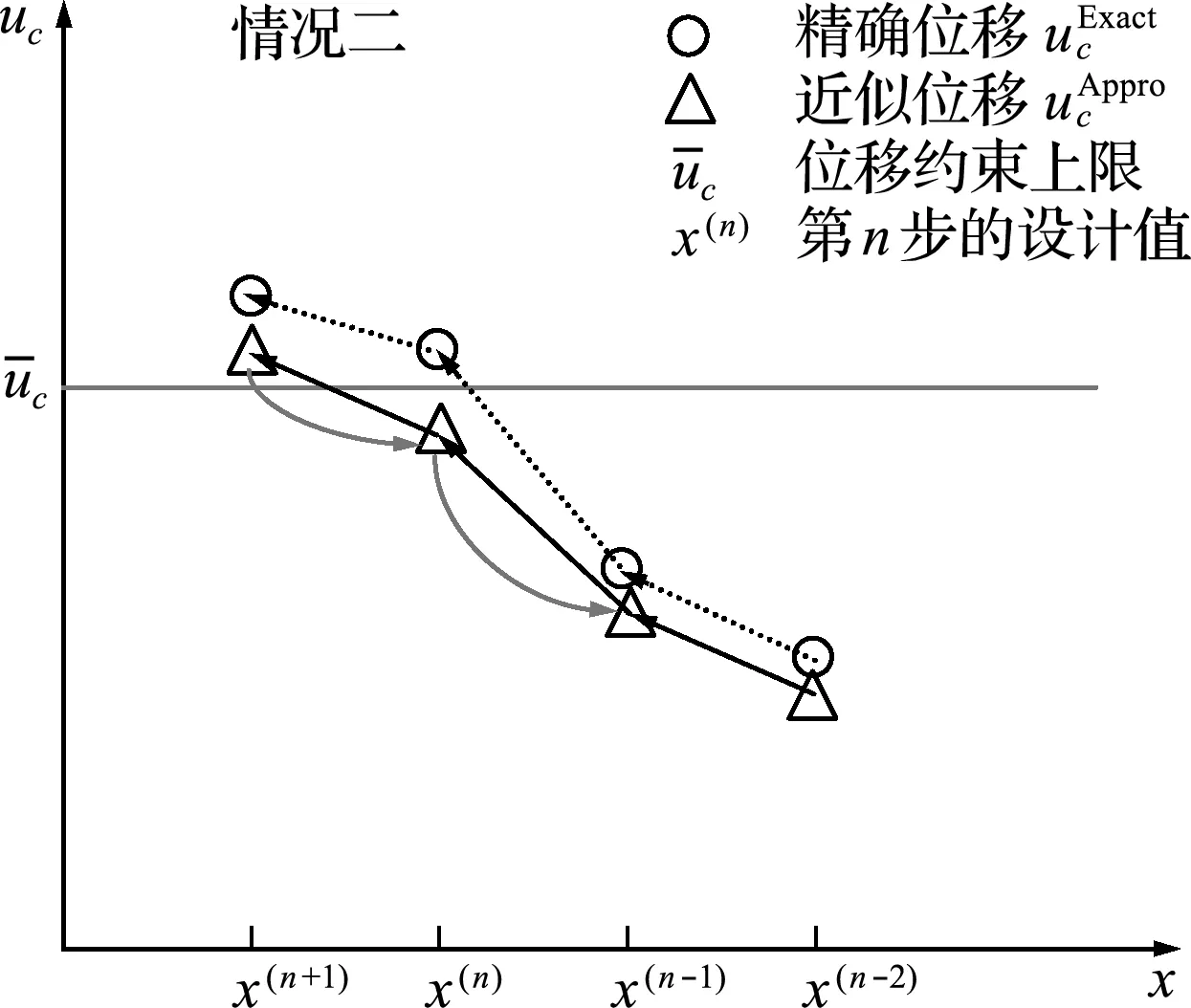
圖9 離散魯棒優化問題收斂過程(二)

3.3 離散魯棒優化問題的數值算例

算例329桿桁架結構

圖10 29桿離散魯棒優化問題目標函數的迭代曲線

表3 離散魯棒優化和連續魯棒優化最優解的比較(單位：cm2)

算例451桿桁架結構

如圖7所示的51桿桁架，規定所有桿件的橫截面積為[3,100]的整數值。外載荷和約束條件等與算例2相同。表4列出了離散魯棒優化和連續魯棒優化所得的最優橫截面積及結構重量等的比較。由表4可知，離散魯棒優化得到的最優解能夠滿足魯棒性約束條件，且與連續魯棒優化最優解的目標函數非常接近，保證了其最優性。

表4 離散魯棒優化和連續魯棒優化最優解的比較(單位：cm2)

4 結 論

本文提出了與離散優化列式等價的魯棒優化列式，并證明了兩者的等價性。把可置信性魯棒結構優化思想應用到離散優化中，提出了用于解決離散優化問題的魯棒圓整法，并進一步拓展到考慮剛度不確定性的離散魯棒優化中。魯棒圓整法首先通過可置信性單層NLSDP算法求解所構造的魯棒優化問題得到連續最優解，然后在魯棒性區域內進行圓整得到可理論上保證滿足約束條件的離散解，最后利用相對差商規則或者相對靈敏度商規則進行修正，得到一階離散局部最優解。相對于傳統的連續優化圓整法來說，本文提出的魯棒圓整法的優勢是能夠嚴格保證離散解的可行性。此外，本文提出的結構可置信性離散魯棒優化方法在計算耗費上和連續魯棒優化相似，因而具有較大的應用價值。

參考文獻(References):

[1] 加里，約翰遜.計算機和難解性[M].張立昂，沈 泓,譯.北京:科學出版社,1987.(Garey M R,Johnson D S.ComputersandIntractability[M].ZHANG Li-ang,SHEN Hong,translated.Beijing:Science Press,1987.(in Chinese))

[2] Papadimitriou C H,Steiglitz K.組合最優化算法和復雜性[M].北京:清華大學出版社,1988.(Papadi-mitriou C H,Steiglitz K.CombinatorialOptimization:AlgorithmsandComplexity[M].Beijing:Tsinghua University Press,1988.(in Chinese))

[3] 隋允康,袁曉兵,葉寶瑞,等.力學映射下板殼結構的截面離散優化設計[J].工程力學,2006,23(8):1-5,11.(SUI Yun-kang,YUAN Xiao -bing.YE Bao -rui,et al.Discrete optimized design of shell structures based on mechanics mapping[J].EngineeringMechanics,2006,23(8):1-5,11.(in Chinese))

[4] Arora J S,Huang M W,Hsieh C C.Methods for optimization of nonlinear problems with discrete variables:A review[J].StructuralOptimization,1994,8(2-3):69-85.

[5] 陳立周.工程離散變量優化設計方法原理與應用[M].北京:機械工業出版社,1989.(CHEN Li-zhou.EngineeringDiscreteVariableOptimizationDesignMethodPrincipleandApplication[M].Beijing:China Machine Press,1989.(in Chinese))

[6] Chai S,Sun H C.A relative difference quotient algorithm for discrete optimization[J].StructuralOptimization,1996,12(1):46-56.

[7] Templeman A B,Yates D F.A linear programming approach to the discrete optimum design of trusses[J].EngineeringOptimization,1982.

[8] 李興斯,譚 濤.離散變量結構優化設計的連續化方法[J].應用力學學報,2007,24(1):26-30，171.(LI Xing-si,TAN Tao.Continuous approach to discrete structural optimization design with discrete variables[J].ChineseJournalofAppliedMechanics,2007,24(1):26-30，171.(in Chinese))

[9] 譚 濤.離散變量優化設計的連續化方法研究[D].大連:大連理工大學,2006.(TAN Tao.Research on Continuous Method of Discrete Variable Optimization Design[D].Dalian University of Technology,2006.(in Chinese))

[10] 石連拴,柴 山,孫煥純.離散變量結構優化設計序列定界組合算法研究[J].大連理工大學學報,1999,39:591-596.(SHI Lian-shuan,CHAI Shan,SUN Huan-chun.Application of a sequential delimitative and combinatorial algorithm to discrete optimum design of structures[J].JournalofDalianUniversityofTechnology,1999,39(5):591-596.(in Chinese))

[11] 王躍方,孫煥純.離散變量桁架結構的布局優化設計[J].大連理工大學學報,1995,35(4):458-462.(WANG Yue -fang,SUN Huan-chun.On layout optimization of truss structures with discrete sizing variables[J].JournalofDalianUniversityofTechnology,1995,35(4):458-462.(in Chinese))

[12] Juang D S,Chang W T.A revised discrete Lagran-gian-based search algorithm for the optimal design of skeletal structures using available sections[J].StructuralandMultidisciplinaryOptimization,2006,31(3):201-210.

[13] Wolkowicz H,Anjos M F.Semidefinite programming for discrete optimization and matrix completion problems[J].DiscreteAppliedMathematics,2002,123(1-3):513-577.

[14] Bertsimas D,Sim M.Robust discrete optimization and network flows[J].MathematicalProgramming,2003,98(1-3):49-71.

[15] Royset J O,Der Kiureghian A,Polak E.Reliability-based optimal design of series structural systems[J].JournalofEngineeringMechanics,2001,127(6):607-614.

[16] Ben-Tal A,Nemirovski A.Robust solutions of Linear Programming problems contaminated with uncertain data[J].MathematicalProgramming,2000,88(3):411-424.

[17] Ben-Tal A,Nemirovski A.Robust convex optimization[J].MathematicsofOperationsResearch,1998,23(4):769-805.

[18] Ben-Tal A,Nemirovski A.Robust solutions of uncertain linear programs[J].OperationsResearchLetters,1999,25(1):1-13.

[19] El Ghaoui L,Lebret H.Robust solutions to least-squares problems with uncertain data[J].SIAMJournalonMatrixAnalysisandApplications,1997,18(4):1035-1064.

[20] El Ghaoui L,Oustry F,Lebret H.Robust solutions to uncertain semidefinite programs[J].SIAMJournalonOptimization,1998,9(1):33-52.

[21] Boyd S,Vandenberghe L.ConvexOptimization[M].Cambridge:Cambridge University Press,2004.

[22] Ben-Tal A,Nemirovski A.Robust optimization -methodology and applications[J].MathematicalPro-gramming,2002,92(3):453-480.

[23] Calafiore G,El Ghaoui L.Ellipsoidal bounds for uncertain linear equations and dynamical systems[J].Automatica,2004,40(5):773-787.

[24] Chen S H,Wu J,Yu Y D,et al.Interval optimization for uncertain structures[J].FiniteElementsinAn-alysisandDesign,2004,40:1379-1398.

[25] Guo X,Du J M,Gao X X.Confidence structural robust optimization by non-linear semidefinite pro -gramming-based single -level formulation[J].InternationalJournalforNumericalMethodsinEnginee-ring,2011,86(8):953-974.

[26] Kang Z,Bai S.On robust design optimization of truss structures with bounded uncertainties[J].StructuralandMultidisciplinaryOptimization,2013,47(5):699-714.

[27] Bai S,Kang Z.Robust topology optimization for structures under bounded random loads and material uncertainties[J].Computers&Structures,2021,252:106569.

[28] Guo X,Bai W,Zhang W S,et al.Confidence structural robust design and optimization under stiffness and load uncertainties[J].ComputerMethodsinAppliedMechanicsandEngineering,2009,198(41-44):3378-3399.

[29] Liu J T,Gea H C.Robust topology optimization under multiple independent unknown-but-bounded loads[J].ComputerMethodsinAppliedMechanicsandEngineering,2018,329:464-479.

[30] Guo X,Bai W,Zhang W S.Extreme structural response analysis of truss structures under material uncertainty via linear mixed 0-1 programming[J].InternationalJournalforNumericalMethodsinEngineering,2008,76(3):253-277.

[31] Du J M,Du Z L,Wei Y H,et al.Exact response bound analysis of truss structures via linear mixed 0-1 programming and sensitivity bounding technique[J].InternationalJournalforNumericalMethodsinEngineering,2018,116(1):21-42.

[32] McWilliam S.Anti-optimisation of uncertain structures using interval analysis[J].Computers&Structures,2001,79(4):421-430.